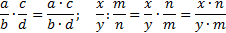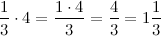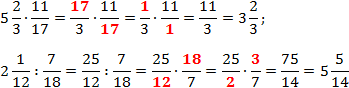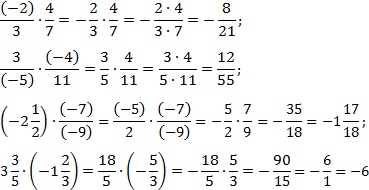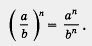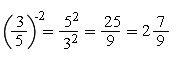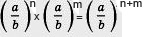в каком классе проходят десятичные числа
Прохождение программы курса математики 5–6-х классов за 1,5 учебных года
Разделы: Математика
Математическое образование в нашей стране получают все школьники, начиная с первого года обучения и до последнего. Само собой разумеется, что лишь небольшая часть обучающихся впоследствии станет сама развивать математику. Но применять математические знания и методы станут все. Очень важно, чтобы учащиеся видели прикладные возможности всех разделов математики и почувствовали значение строгих логических рассуждений для всех видов деятельности.
Как же строится школьный курс математики?
В курсе математики для V-XI кл. с учётом возрастных особенностей выделяются три ступени обучения: V-VI, VII-IX, X-XI классы.
В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, с положительными и отрицательными числами, знакомятся с буквенными выражениями, учатся составлять по условию текстовой задачи несложные линейные уравнения и решать их.
Следует отметить, что в V классе слишком много времени уделяется (по стандартной программе) повторению изученного в начальной школе.
Чтобы преодолеть такое положение вещей, делаются различные попытки, одной из которых является разработанная Г.Г. Левитасом переходная программа. Она рассчитана на изучение курса V-VI классов за один учебный год при пяти часах математики в неделю. Изучение этой программы предложено вести по учебникам Н.Я. Виленкина. При этом в течении каждой четверти программа строится из расчёта один пятиурочный цикл в неделю.
Нами было разработано планирование, рассчитанное на изучение математики в V кл. при четырёх часах в неделю, а в VI кл. при пяти часах в неделю. В пятом классе пятый час в неделю может быть использован учителем на свое усмотрение. В зависимости от уровня математической подготовки учащихся, им могут быть предложены задания развивающего характера или задания на ликвидацию пробелов по изучаемой теме. Программа рассчитана на изучение материала V-VI классов за 1,5 учебных года, и поэтому в VI классе со II полугодия необходимо приступать к изучению материала VII класса.
В рамках V класса изучаются следующие темы: натуральные числа (повторение изученного в начальной школе), обыкновенные и десятичные дроби.
В VI классе: отрицательные и положительные числа, пропорции и проценты, решение уравнений и координатная плоскость.
5 КЛАСС
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА ПО КУРСУ «МАТЕМАТИКА» В 5-КЛАССЕ (ПО ЧЕТВЕРТЯМ).
I четверть 9*4 ч.=З6 ч.
| № уроков | Содержание | Кол-во уроков |
| 1-12 | Действия с натуральными числами. | 12 |
| 13-16 | Свойства действий с натуральными числами. | 4 |
| 17-20 | Решение уравнений. | 4 |
| 21-30 | Решение задач (типа «во ск.», «на ск.», больше-меньше; «на», «в», на движение). | 10 |
| 31 | Подготовка к контрольной работе. | 1 |
| 32 | Контрольная работа №1 | 1 |
| 33-36 | Десятичная система исчисления, меры длины. | 4 |
II четверть 7*4 ч.=28 ч.
| № уроков | Содержание | Кол-во уроков |
| 36-39 | Что такое десятичная дробь. Сравнение десятичных дробей. | 4 |
| 40-43 | Сложение и вычитание десятичных дробей. | 4 |
| 44-46 | Решение уравнений. | 3 |
| 47 | Подготовка к контрольной работе. | 1 |
| 48 | Контрольная работа № 2. | 1 |
| 49-52 | Умножение десятичных дробей. | 4 |
| 53-56 | Деление десятичных дробей. | 4 |
| 57-59 | Решение уравнений. | 3 |
| 60 | Подготовка к контрольной работе. | 1 |
| 61 | Контрольная работа № 3. | 1 |
| 62-63 | Округление десятичных дробей. Прикидка | 2 |
III четверть 10*4 ч.=40 ч.
| № уроков | Содержание | Кол-во уроков |
| 64-66 | Обыкновенная дробь. Сравнение на луче. | 3 |
| 67-68 | Правильные и неправильные дроби. Сравнение с 1. | 2 |
| 69-72 | Признаки делимости. Разложение на простые множители. НОД. | 4 |
| 73-76 | Основное свойство. Сокращение дробей. | 4 |
| 77-80 | Сложение, вычитание и сравнение дробей с одинаковыми знаменателями. | 4 |
| 81 | Подготовка к контрольной работе. | 1 |
| 82 | Контрольная работа №4. | 1 |
| 83-86 | НОК. Приведение к общему знаменателю. | 4 |
| 87-90 | Сравнение, сложение и вычитание дробей с разными знаменателями. | 4 |
| 91-93 | Решение уравнений. | 3 |
| 94 | Подготовка к контрольной работе. | 1 |
| 95 | Контрольная работа №5. | 1 |
| 96-99 | Умножение обыкновенных дробей. | 4 |
| 100-104 | Деление обыкновенных дробей. | 4 |
IV четверть 8*4 ч.=32ч.
| № уроков | Содержание | Кол-во уроков |
| 105-107 | Решение уравнений. | 3 |
| 108 | Подготовка к контрольной работе. | 1 |
| 109 | Контрольная работа №6. | 1 |
| 110-113 | Смешанные числа. | 4 |
| 114-117 | Три задачи на дроби. | 4 |
| 118-121 | Решение текстовых задач (составление уравнений, проценты). | 4 |
| 122 | Подготовка к контрольной работе. | 1 |
| 123 | Контрольная работа №7. | 1 |
| 124-127 | Все действия обыкновенными и десятичными дробями. | 4 |
| 128-134 | Повторение. Итоговая контрольная работа. | 7 |
6 КЛАСС
Из программы 6 класса осталось пройти следующие темы: «Положительные и отрицательные числа», «Решение уравнений», «Координатная плоскость», «Пропорция».
За I четверть изучаются положительные и отрицательные числа, координатная плоскость. Первые уроки четверти посвящаются повторению пройденного в 5 классе.
II четверть начинается с изучения темы: «Решение уравнений», а затем до конца четверти учащиеся занимаются нахождением неизвестного члена пропорции и решают задачи на прямую и обратную пропорциональную зависимость.
С окончанием II четверти заканчивается изучение материала 6-го класса.
Десятичные дроби
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
В каком классе проходят десятичные дроби?
По сравнению с программой времен СССР дети уже даже к 1 классу идут подготовленные. Есть школы разные и разные уклоны. Если школа с математическим уклоном, то с понятиями дробей детей знакомят на поверхностном уровне уже в третьем классе, а уже в пятом классе они начинают полноценно изучать дроби. Десятичные дроби уже могут дать в четвертом классе, а обычные в пятом. Именно в пятом классе дети учат числитель, знаменатель и т.п.
Моя премянница в третьем классе их проходит. Точнее, пару недель назад прошла. Вместе с обычными дробями.
А я, помнится, дроби раза три проходил. Когда-то в начальной школе, потом в пятом классе, а потом ещё в 7-ом. Может тогда и отличались названия тем уроков, но выглядело все одинаково.
В начальной школе ученики только поверхностно знакомятся с дробями. В 4 классе у них есть тема «задачи на нахождение части от целого и целого по части». Это что-то типа: найти «3/4 от 520» и т.п. Но как такого понятия «дроби» они еще не знают. И только в пятом классе они узнают, что такое знаменатель, числитель и т.д.
Программа меняется часто, то что проходят в России в других странах проходят гораздо позднее. В Швеции в Италии таблицу умножения проходят чуть ли не с шестого класса. А мы учили ее в начальной школе.
В российских школах десятичные дроби начинают изучать в пятом классе. Пока у нас школьная программа сильнее.
Сейчас, когда дети идут в школу, то умеют писать, считать и читать. Поэтому программа, которая была у нас, более взрослого поколения, устаревает. Современные дети начинаются знакомиться с дробями в первом классе (более упрощенный вариант), потом более сложные дроби начинают проходить с третьего класса.
Десятичные дроби проходят на класс раньше, чем обыкновенные.
Отмечу, что в четвертом-пятом классах начинают уже решать с ними примеры, а вот понятие дробей могут давать раньше.
Да что говорить, мою племяшку еще в детском садике обыкновенным дробям учили, а они, в общем-то, от десятичных отличаются только записью.
Тут многое зависит какая школа и если школа не математическая и ребенок в ней, учится не перескакивая через классы, то чаще всего, это 4 класс, а если школа математическая и ребенок минует 4 класс не учась в нем, то тогда, начинают чаще с 3 класса.
Важно учитывать какая школа, да и школьные программы довольно часто меняются, могут быть нюансы.
Но если в целом, то десятичные дроби изучают с 4 класса (точней, проходят) в некоторых школах с 3 класса.
Ну и конечно важно учитывать о какой стране вообще идёт речь.
Понятие десятичной дроби начинают объяснять уже в 3 классе. Понемногу приучают ученика к теме: делят с помощью рисунков и используя спички и полоски бумаги. Полностью десятичные дроби изучаются в 5 классе, когда ребенок будет готов к пониманию определения.
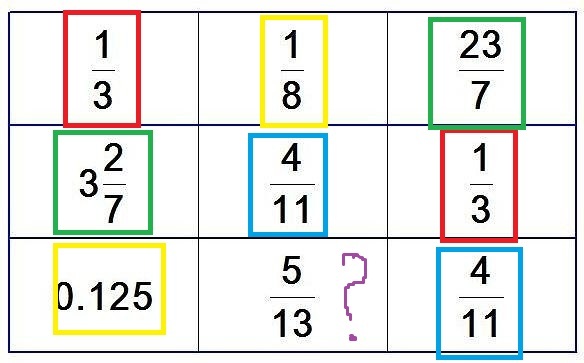
Объясняю: каждое число в таблице имеет свою пару, кроме 5/13
0.125 это десятичная запись дроби 1/8
3 и 2/7 это то же самое, что и 23/7
Остальные числа видны и так, для наглядности предоставлю скрин:
Отвечать на такие вопросы на БВ тяжело, по причине отсутствия шрифтов при помощи которых можно писать дроби. Приходится использовать чужие примеры.
В общем случае умножение и деление дробей происходит по следующему правилу
Несмотря на такую простоту здесь достаточно возможностей для совершения ошибок.
При умножении целого числа на дробь следует помнить что любое целое число должно быть представлено в виде дроби 5/1, 12/1, 48/1 и так далее. Поэтому 1/3 умножают на 4/1 где 1 можно упустить.
Одна целая часть любой дроби равна дроби где числитель и знаменатель равны и имеют значение знаменателя общей дроби.
При использовании отрицательных чисел помним: если в числителе или знаменателе минус то и вся дробь будет с минусом, а если и в числителе и в знаменателе минус то дробь будет с плюсом.
При перемножении дробей в степени их можно преобразовать следующим образом.
Переворот дроби ведет к изменению знака степени.
При умножении двух одинаковых дробей с разными степенями получаем туже дробь в степени являющейся суммой степеней первой и второй дроби.
При сокращении дробей нельзя сокращать члены объединенные между собой знаками плюс и минус. Можно только знаком умножения! Ниже приведено не верное решение.
Урок математики в 5-м классе. Тема: «Понятие десятичной дроби. Чтение и запись десятичных дробей»
Разделы: Математика
Тема: Понятие десятичной дроби. Чтение и запись десятичных дробей.
Цели:
Развивающая цель: Формирование навыков самооценки и самоанализа учебной деятельности.
Проблемно – развивающий урок (комбинированный)
Этапы:
1) проблемная ситуация;
2) проблема;
3) поиск приёмов её решения;
4) решение проблемы
Девиз урока: «Знания имей отличные по теме «Дроби десятичные»
Задача урока: доказать, что дроби не смогут поставить нас в трудное положение.
Эпиграфы:
«Математику нельзя изучать, наблюдая, как это делает сосед»
(поэт Нивей)
«Учиться надо весело… Чтобы переваривать знания, надо поглощать их с аппетитом»
(Анатоль Франс)
Оборудование:
Повторение:
Ход урока
Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед. Поэтому будем сегодня работать все активно, хорошо и с пользой для ума.
Первый тур
Второй тур «Логические цепочки»
Расположи в порядке возрастания.
Третий тур.
Ученик допустил ошибку при применении основного
свойства дроби. Найди ошибку!
Четвёртый тур
1. Всегда ли можно единицу представить в виде обыкновенной дроби?
2. Верно, ли выполнено действие под №5?
3. Чем отличаются примеры под №4 и №5?
Изучение новой темы
Рассмотрим таблицу разрядов и ответим на вопросы:
Вывод:перемещая единицу на один разряд вправо, мы каждый раз уменьшали соответствующее число в 10 раз и делали это, пока не дошли до последнего разряда – разряда единиц.
А можно ли и единицу уменьшить в 10 раз?
Конечно,
Проблема: Но вот места для этого числа в нашей таблиц разрядов пока нет.
Подумайте, как надо изменить таблицу разрядов, чтобы в ней можно записать число 
Рассуждаем, надо цифру 1 сдвинуть вправо на один разряд.

Дать названия разрядам: десятые, сотые, тысячные, десятитысячные и т.д. целая часть дробная часть
Работа по таблице.
Прочитать числа, записанные в таблице.
2 единицы 3 десятых
2 единицы 3 сотых
А чтобы записать числа вне таблицы нам необходимо отделять каким – либо знаком целую часть от дробной. Договорились делать это с помощью запятой или точки. В нашей стране, как правило, используется запятая, а в США и некоторых других странах – точка. Числа записываем и читаем следующим образом:
а) 2,3 или 2.3 (две целых три десятых или два, запятая, три или два, точка, три)
б) 2,03 или 2.03 (две целых три сотых или два, запятая, ноль, три или два, точка, ноль, три)
Правило: Если в десятичной записи числа использованы запятая (или точка), то говорят, что число записано в виде десятичной дроби.
Для краткости числа называют просто десятичными дробями.
Заметим, что десятичная дробь – это не новый тип числа, а новый способ
записи числа.
Итак, девиз нашего урока: «Знания имей отличные по теме «Дроби десятичные»
Задача урока: доказать, что дроби не смогут поставить нас в трудное положение.
А сейчас посетим «Деревню Историческую»
Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби. Действия над дробями в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби». Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввёл в 1585году голландский математик и инженер Симон Стевин. Вот как он изображал дробь:
14,382, 14 0 3 1 8 2 2 3
Во Франции десятичные дроби ввёл Франсуа Виет в 1579 году; его запись дроби: 14,382, 14/382, 14
А у нас учение о десятичных дробях изложил Леонтий Филиппович Магницкий в 1703 году в учебнике математики «Арифметика, сиречь наука числительная»
Вот ещё некоторые способы изображения десятичных дробей:
14. 3. 8. 2. ;
Зарядка (музыкальное сопровождение)
II. Упражнения
III. Переменка – проводится для того, чтобы сохранить хорошее настроение, бодрость духа, математический настрой.
Анатоль Франс когда – то сказал: «Учиться надо весело…Чтобы переваривать знания, надо поглощать их с аппетитом»
Устно:
а) 
Сколько там было усатых солдат?
Сколько там было безусых солдат?
б) 
Сколько там было носатых солдат?
Сколько там было курносых солдат?
Запись: 

IV. Повторение – развивающие упражнения (работа в парах)
Озеро Ребусное ( Приложение)
V. Итог урока.
— Что нового для себя узнали?
— В чём затруднялись?
— Чему научились?
— Какую проблему ставили на уроке?
— Удалось ли нам её решить?
Оценка своей работы (на листочках, где таблицы разрядов). Напишите, как усвоили материал урока.