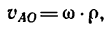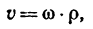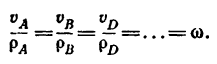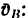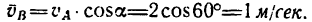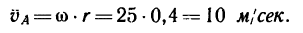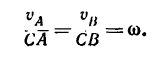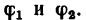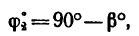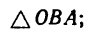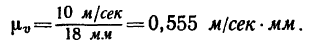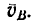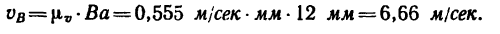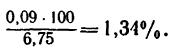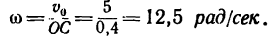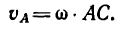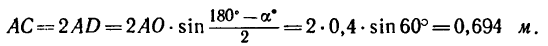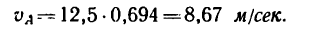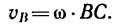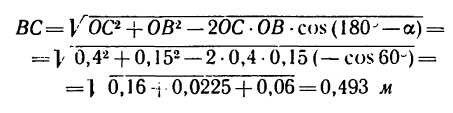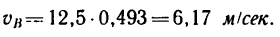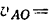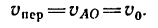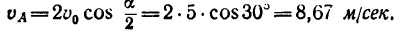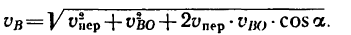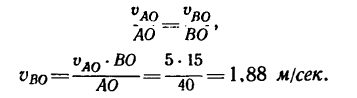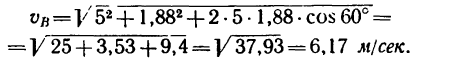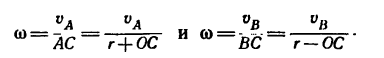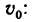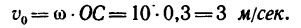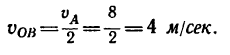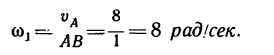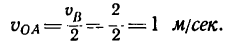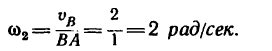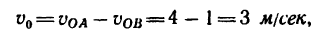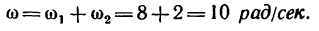что такое параллельное движение
Механизм параллельного движения
Из Википедии — свободной энциклопедии
Механизм параллельного движения — механизм, изобретённый шотландским инженером Джеймсом Уаттом в 1784 году для его парового двигателя двойного действия.
В то время паровые машины ещё не были достаточно совершенными. Однако, на шахтах для откачки воды уже использовались паровые двигатели Ньюкомена (рис. 3). В этой установке мощность вырабатывалась во время хода поршня только в одну сторону (на рисунке — во время движения вниз), и передавалась от двигателя к коромыслу DF посредством цепи. Обратный ход поршня (вверх) был холостым, и поршень поднимался за счёт веса насоса с другой стороны коромысла (со стороны луча EF). В новом паровом двигателе Уатта, который теперь был двигателем двойного действия, мощность вырабатывалась как во время хода поршня вниз, так и вверх. Цепь не могла передавать мощность от двигателя к коромыслу во время хода поршня вверх, поэтому Уатт создал механизм, который передавал мощность от поршня к коромыслу во время хода поршня в обоих направлениях (рис. 1). Уатт назвал его «механизмом параллельного движения», поскольку как насос, так и поршень перемещались вертикально и параллельно друг другу.
В письме к своему сыну в 1808 году Уатт писал:
Я горжусь механизмом параллельного движения больше, чем любым другим своим изобретением, которое я когда-либо сделал
[1]
Как уже было отмечено, движение точки F не является строго прямолинейным, а только весьма близко к нему. Однако описываемый механизм параллельного движения даёт отклонение от прямолинейности примерно на 1/4000 часть. Позже, в 19-м веке, были созданы механизмы, создающие строго прямолинейное движение, первыми из которых были механизм Липкина — Посселье и механизм Саррюса.
Музыкальная теория для чайников: параллельные гармонии
Разбираемся в том, что такое параллельные гармонии, параллельное движение, а также параллельные интервалы и аккорды.
Если по какой-либо причине вы избегаете использования параллельных гармоний в своей музыке, то подумайте еще разок. При правильном использовании параллельные гармонии могут стать крайне эффективным инструментом в руках современного композитора.
Параллельные гармонии могут вызвать неподдельное удивление слушателя, и, к счастью, это именно тот эффект, которого можно добиться при их использовании. Обычно, в традиционной гармонии стараются избегать использования параллельных октав и квинт, но для написания более современной музыки стоит все же пренебречь этим. Разобравшись в голосах и их параллельном движении, а также благодаря аккуратному и своевременному оправданному использованию, параллельные гармонии могут привнести в музыку достаточно интересные ходы.
Давайте взглянем на три варианта использования параллельных гармоний, которые ломают правила музыки, устоявшиеся еще в XVIII веке.
Параллельное движение
Простейшим вариантом применения параллелизма можно назвать параллельное движение. При использовании параллельного движения можно особо не переживать о совместном движении аккордов вверх или вниз в одно и то же время — основное внимание должно уделяться межинтервальным отношениям между звуками.
В данном примере можно заметить, что ноты далеко не всегда «движутся» в одном направлении. Несмотря на это, тональность музыкальной зарисовки остается неизменной (в нашем случае это Фа мажор), а звуки хорошо соотносятся друг с другом.
Конечно, такой пример сложно назвать полноценной параллельной гармонией, но это довольно неплохая отправная точка для освоения этой техники. Разобравшись с принципами этого примера, стоит углубиться в премудрости параллельных гармоний.
Параллельные интервалы
В этом примере сохраняется не только интервал между основными звуками аккорда, но и расстояние между каждым из звуков, входящих в аккорд.
Совсем не обязательно использовать параллельные интервалы только с обычными трезвучиями или простыми устойчивыми интервалами. Можно «наслаивать» и другие интервалы выше последних звуков: к примеру, добавить кварты для создания по истине многослойной текстуры.
Сами по себе интервалы могут звучать достаточно неприятно или даже не разрешённо, но при исполнении (во время «движения» музыки) их звучание станет более понятным.
Параллельные аккорды
Как только вы освоитесь с применением обыкновенного движения и интервалов, самое время браться за что-то более сложное, а именно за использование параллельных аккордов.
Использование параллельных аккордов применяется во многих музыкальных стилях: от популярной и танцевальной музыки и до джаза и рока. В рамках «домашней работы» можно послушать творчество таких композиторов как Клод Дебюсси или Жозефа Мориса Равеля, чтобы понять применение параллельных аккордов на практике.
При использовании параллельных аккордов, каждая нота аккорда движется в рамках одного интервала (каждая нота повышается на полтона, или каждая нота понижается до какого-либо тона), а межинтервальные отношения между индивидуальными аккордами сохраняются. Таким образом, получается нисходящее или восходящее движение аккордов одинаковой или похожей структуры без учета каких-либо правил традиционной гармонии.
Допустим, если вы используете минорный нонаккорд, то и все последующие и параллельные аккорды также должны быть минорными нонаккордами. При таком положении вещей придется использовать аккорды вне тональности музыкального произведения, над которым вы работаете, но это совершенно нормально.
Заключение
Пытаясь применить параллельные гармонии в собственной музыке, постарайтесь начать с малого: используйте их аккуратно, по чуть-чуть и только в тех случаях, когда это будет оправдано.
Использование мелодий с параллельными аккордами в аккомпанементе может стать хорошим подспорьем в создании необычных и удивительных проигрышей в середине песни, а также привлечь дополнительное внимание слушателей в те моменты, когда с этим не может справиться традиционная музыкальная гармония.
параллельное движение
Смотреть что такое «параллельное движение» в других словарях:
ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ — См. Движение, 3 … Музыкальный словарь Римана
параллельное движение катализатора и перерабатываемого сырья — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN cocurrent catalyst flow … Справочник технического переводчика
ПЛОСКО-ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ — движение твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости … Большой Энциклопедический словарь
ПЛОСКО-ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ — ПЛОСКО ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ, движение твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости … Энциклопедический словарь
Параллельное Кино — андерграундное направление в советском кинематографе, сформировавшееся вопреки канонам как официального искусства, так и авторского кино. Зарождение П. К. можно отнести к рубежу 1970 1980 х годов, когда, преимущественно в Москве и Ленинграде,… … Альтернативная культура. Энциклопедия
ФЛАНГОВОЕ ДВИЖЕНИЕ ВОЙСК — параллельное фронту противника; имеет целью соединение двух отдельно действующих отрядов, обход неприятеля с фланга и др. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907 … Словарь иностранных слов русского языка
ТЕРМИНЫ МУЗЫКАЛЬНЫЕ — Словарь содержит наиболее употребительные термины. См. также МУЗЫКАЛЬНАЯ ФОРМА; МУЗЫКАЛЬНЫЕ ИНСТРУМЕНТЫ; МУЗЫКИ ТЕОРИЯ. В итальянских терминах языковая принадлежность не указывается. АВТЕНТИЧЕСКИЙ 1) автентический каданс в мажоро минорной системе … Энциклопедия Кольера
Индикатор — (Indicator) Индикатор это информационная система, вещество, прибор, устройство, отображающий изменения какого либо параметра Индикаторы графиков валютного рынка форекс, какие они бывают и где их можно скачать? Описание индикаторов MACD,… … Энциклопедия инвестора
Хеджирование — (Hedge) Хеджирование это операция, которая предназначена снизить риск, возникший в результате других операций Что такое хеджирование валютных и финансовых рисков опционами и фьючерсами, методы хеджирвоания сделок, инструменты хеджирвоания… … Энциклопедия инвестора
Российская Советская Федеративная Социалистическая Республика — РСФСР. I. Общие сведения РСФСР образована 25 октября (7 ноября) 1917. Граничит на С. З. с Норвегией и Финляндией, на З. с Польшей, на Ю. В. с Китаем, МНР и КНДР, а также с союзными республиками, входящими в состав СССР: на З. с… … Большая советская энциклопедия
ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ
Смотреть что такое «ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ» в других словарях:
параллельное движение — восходящее или нисходящее параллельное движение двух и более голосов, при котором между этими голосами сохраняется одно и то же интервальное расстояние (напр. движение параллельными терциями или паралелльными квартами) … Русский индекс к Англо-русскому словарь по музыкальной терминологии
параллельное движение катализатора и перерабатываемого сырья — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN cocurrent catalyst flow … Справочник технического переводчика
ПЛОСКО-ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ — движение твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости … Большой Энциклопедический словарь
ПЛОСКО-ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ — ПЛОСКО ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ, движение твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости … Энциклопедический словарь
Параллельное Кино — андерграундное направление в советском кинематографе, сформировавшееся вопреки канонам как официального искусства, так и авторского кино. Зарождение П. К. можно отнести к рубежу 1970 1980 х годов, когда, преимущественно в Москве и Ленинграде,… … Альтернативная культура. Энциклопедия
ФЛАНГОВОЕ ДВИЖЕНИЕ ВОЙСК — параллельное фронту противника; имеет целью соединение двух отдельно действующих отрядов, обход неприятеля с фланга и др. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907 … Словарь иностранных слов русского языка
ТЕРМИНЫ МУЗЫКАЛЬНЫЕ — Словарь содержит наиболее употребительные термины. См. также МУЗЫКАЛЬНАЯ ФОРМА; МУЗЫКАЛЬНЫЕ ИНСТРУМЕНТЫ; МУЗЫКИ ТЕОРИЯ. В итальянских терминах языковая принадлежность не указывается. АВТЕНТИЧЕСКИЙ 1) автентический каданс в мажоро минорной системе … Энциклопедия Кольера
Индикатор — (Indicator) Индикатор это информационная система, вещество, прибор, устройство, отображающий изменения какого либо параметра Индикаторы графиков валютного рынка форекс, какие они бывают и где их можно скачать? Описание индикаторов MACD,… … Энциклопедия инвестора
Хеджирование — (Hedge) Хеджирование это операция, которая предназначена снизить риск, возникший в результате других операций Что такое хеджирование валютных и финансовых рисков опционами и фьючерсами, методы хеджирвоания сделок, инструменты хеджирвоания… … Энциклопедия инвестора
Российская Советская Федеративная Социалистическая Республика — РСФСР. I. Общие сведения РСФСР образована 25 октября (7 ноября) 1917. Граничит на С. З. с Норвегией и Финляндией, на З. с Польшей, на Ю. В. с Китаем, МНР и КНДР, а также с союзными республиками, входящими в состав СССР: на З. с… … Большая советская энциклопедия
Плоскопараллельное движение тела в теоретической механике
Плоскопараллельное движение тела:
Сложное плоскопараллельное движение твердого тела составляется из поступательного и вращательного движений. Это свойство является основой первого способа определения скорости любой точки тела, находящегося в плоскопараллельном движении.
1. Поступательная часть плоскопараллельного движения принимается за переносное и зависит от движения какой-либо произвольно выбранной точки, называемой полюсом. За полюс принимают всегда ту точку, скорость которой в данный момент известна.
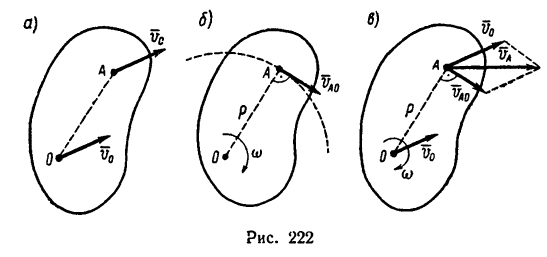
Если движение является только поступательным, то все точки тела, в том числе и точка А (рис. 222, а), имеют ту же скорость, что и полюс О.
2. Вращательная часть плоскопараллельного движения вокруг выбранного полюса принимается за относительное.
Если движение тела является только вращательным, то точка А совершает движение по окружности с центром в полюсе О со скоростью
3. Абсолютная скорость 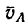
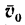
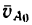
Второй способ определения скорости любой точки тела при его плоскопараллельным движении основан на использовании в качестве полюса мгновенного центра скоростей.
1. Как известно, мгновенным центром скоростей называется расположенная в плоскости сечения точка, абсолютная скорость которой в данный момент равняется нулю.
2. Если за полюс принять мгновенный центр скоростей, то в этот момент переносные (поступательные) скорости всех точек тела равны нулю и абсолютная скорость любой точки определяется по формуле
где 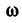
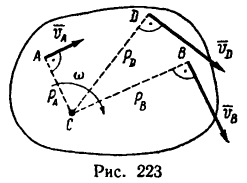
р—расстояние от мгновенного центра скоростей С до данной точки (рис. 223).
Для скоростей любых точек сечения имеем зависимость
При решении некоторых задач оказывается целесообразным использовать теорему о равенстве между собой проекций скоростей двух точек плоского сечения на прямую, соединяющую эти точки.
Задача №1
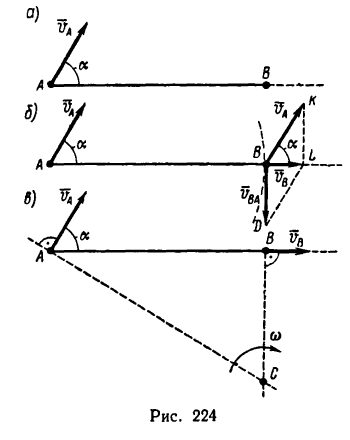
Стержень АВ двигается в плоскости чертежа. В момент, когда стержень занимает горизонтальное положение (рис. 224, а), скорость его точки А равна 2 м/сек и направлена под углом а=60° к прямой АВ. Определить скорость точки В, если известно, что она направлена вдоль АВ.
Решение 1—сложение переносной и относительной скоростей (рис. 224, б).
1. Примем за полюс точку А. Вместе с полюсом стержень АВ движется поступательно, поэтому точка В как слагаемая скорость имеет скорость полюса, т. е. 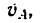
2. Вследствие вращения стержня вокруг полюса точка В имеет вторую слагаемую скорость 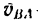
3. Построим параллелограмм скоростей. В параллелограмме известно направление диагонали, которая изобразит искомую скорость 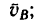
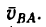
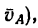
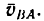
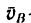
4. Находим числовое значение

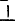
Решение 2 — при помощи мгновенного центра скоростей (рис. 224, в).
1. Из точек А и В проведем две прямые, перпендикулярные к направлениям скоростей 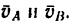
2. Вращение стержня АВ вокруг мгновенного центра скохарактеризуется угловой скоростью 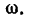
Поэтому
Отсюда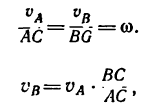
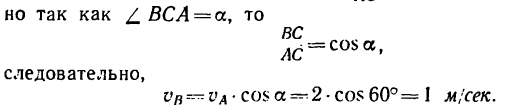
Решение 3—с применением теоремы о проекциях скоростей двух точек плоского сечения.
1. В рассматриваемом случае искомая скорость 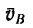
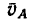
2. Спроектировав данную скорость 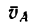
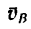
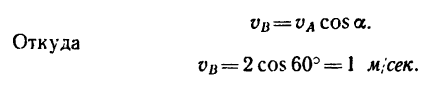
При решении подобных задач иногда приходится выполнять довольно много промежуточных вычислений. Их можно избежать, если решить задачу графическим методом, но с приближенным результатом.
Поясним это на примере следующей задачи.
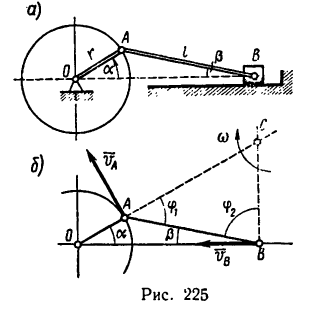
Задача №2
Кривошип 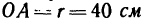
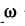
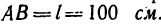
Решение 1 — при помощи мгновенного центра скоростей (решение путем сложения переносной и относительной скоростей рекомендуется выполнить самостоятельно).
1. Изобразим на рис. 225, б расчетную схему. Схематично покажем кривошип ОА и шатун АВ в заданном положении. Ползун В, можно отождествить с точкой В.
2. Замечаем, что кривошип cobcj ползун В движется поступательно, ■ параллельное движение.
3. Скорость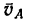
Скорость 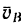
Проведем из точек А и В пря правлениям скоростей 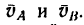
4. Найдя положение мгновенноп центра скоростей, получим = 0).
Отсюда 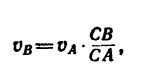
но предварительно нужно узнать значение отношения 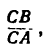
как легко заметить, равно отношению синусов противолежащих углов (теорема синусов):
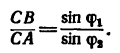
5. Чтобы определить величину этого отношения, необходимо определить углы
Замечая, что (см. рис. 225, б)
найдем угол 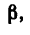
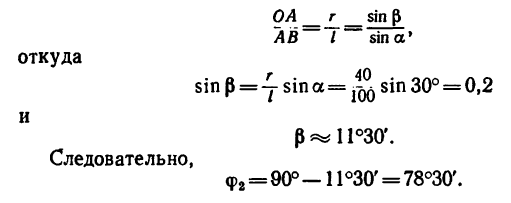
Из того же рис. 225, б видно, что угол 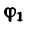

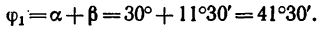
6. Теперь можно определить числовое значение скорости ползуна В:
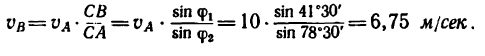
Решение 2—графическим методом.
1. Построим в масштабе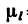
2. Скорость 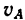
3. Из точки В построим вектор 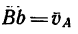
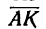
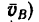
4. Измерив длину отрезка Ва, найдем, что Ва — 12 мм. Следовательно, числовое значение скоростей точки В
5. Как видно, между результатом, вычисленным при помощи мгновенного центра скоростей (6,75), и результатом, найденным при графическом решении (6,66), имеется расхождение, равное
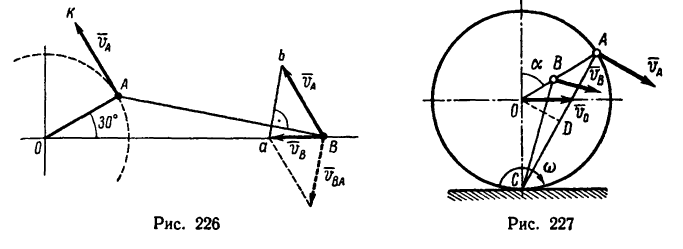
0,09 (абсолютная ошибка). Следовательно, относительная ошибка, допущенная в графическом решении, составляет
Задача №3
Колесо катится без скольжения по горизонтальной плоскости, причем ось колеса перемещается равномерно со скоростью 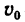
Решение 1—при помощи мгновенного центра скоростей.
1. Колесо катится без скольжения, следовательно, точка С соприкосновения колеса с горизонтальной плоскостью является мгновенным центром скоростей, так как абсолютная скорость этой точки ос=0 Если принять точку С за полюс, то можно считать, что в данный момент колесо совершает вращение вокруг так называемой мгновенной оси, перпендикулярной к плоскости колеса и проходящей через точку С (мгновенный центр скоростей).
2. Определяем угловую скорость колеса:
3. Определяем абсолютную скорость точки А. Скорость направлена перпендикулярно к прямой АС, соединяющей точку А с мгновенным центром скоростей С,
4. Определяем абсолютную скорость точки В. Скорость у0 направлена перпендикулярно к примой СВ и численно равна
Решение 2 —при помощи сложения переносной и относительной скоростей.
1. Катящееся колесо совершает сложное движение, складывающееся из поступательного движения колеса вместе с осью О (переносного движения) и вращения колеса вокруг оси О (относительного движения).
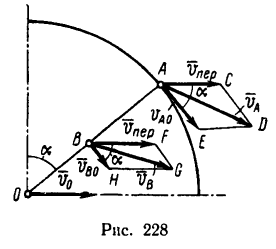
2. Абсолютная скорость 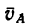
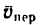
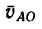
3. Переносная скорость точки А равна скорости 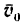
Найдем относительную скорость
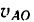
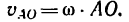
точку С (см. рис. 227), найдем, что 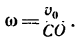
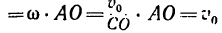
Таким образом, для точки, расположенной на ободе катящегося без скольжения колеса,
^пер — Vao === Последовательно, параллелограмм ACDE есть ромб с углом САЕ = а = 60°, поэтому
4. Абсолютная скорость vB точки В равна диагонали параллелограмма BFGH, построенного на переносной скорости 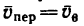
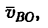
Но предварительно необходимо найти скорость 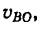
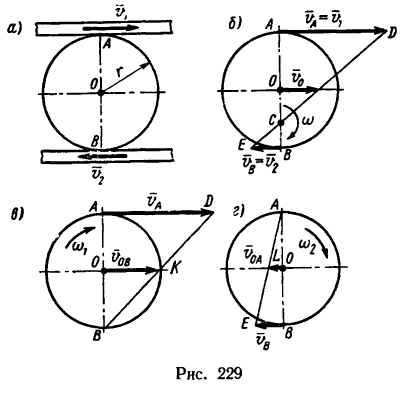
Задача №4
Две параллельные рейки (рис. 229, а) движутся в противоположные стороны с постоянными скоростями 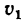
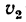
Найти угловую скорость диска и скорость его центра.
Решение 1— при помощи мгновенного центра скоростей.
2. Скорость 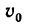
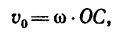
где 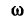
3. Величины угловой скорости 
Так как левые части обоих равенств равны между собой, то 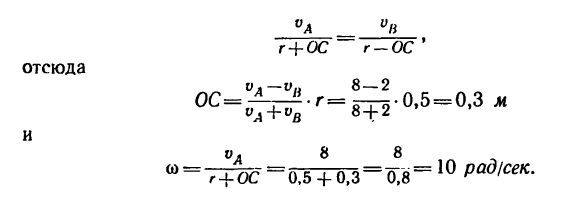
4. Находим скорость
Решение 2—методом последовательной остановки реек.
1. Плоское движение диска образуется вследствие независим мого друг от друга перемещения реек. Поэтому скорость центра диска можно получить как результат геометрического сложения скоростей, получаемых точкой О от перемещения каждой рейки.
2. Мысленно остановим нижнюю рейку (рис. 229,в). Тогда благодаря передвижению верхней рейки диск будет катиться по нижней без скольжения и в точке В образуется мгновенный центр скоростей.
Соединим точку В с точкой D (концом вектора 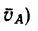
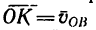
Так как ОК — средняя линия треугольника BAD,
Угловая скорость диска в этом движении
3. Теперь мысленно остановим верхнюю рейку (рис. 229 г). Диск будет катиться без скольжения по верхней рейке, имея мгновенный центр скоростей в точке А.
Соединив точку А с концом Е вектора 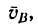
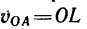
Угловая скорость диска в этом движении
4. При одновременном движении обеих реек скорость центра диска
так как обе скорости 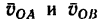
5. Угловая скорость диска определяется как сумма угловых скоростей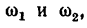
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.