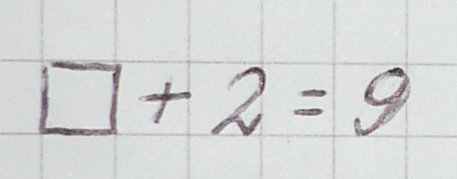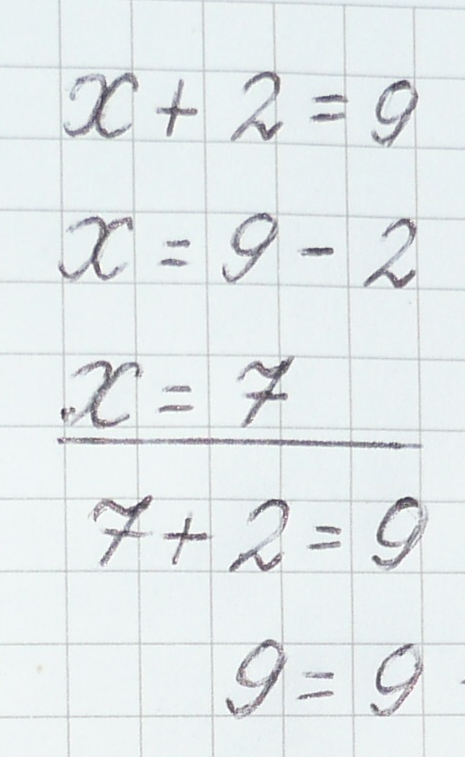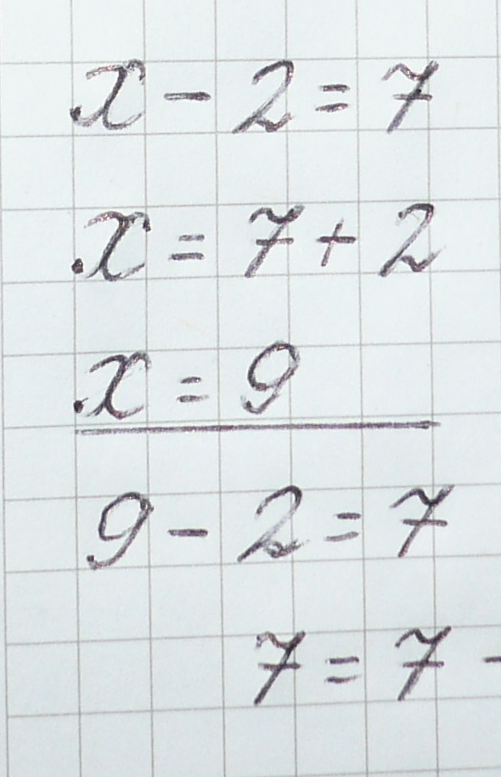в каком классе изучают уравнения с одним неизвестным
Урок математики по теме «Знакомство с уравнениями» по программе «Школа России»
Цели:
Методы обучения: частично- поисковый, проблемного изложения материала.
Формы организации учебной деятельности: фронтальная, индивидуальная, парная.
Средства обучения: М.И. Моро «Математика» 2 класс, 2 части, Москва, «Просвещение», 2006.
Ход урока
I. Организационный момент.
II. Устные задания:
III. Изучение новой темы.
С новой темой познакомится класс
Сегодня узнаем без сомненья
Имя этого выражения: х+4 = 12
А для этого нужно расшифровать слово, решив примеры.
У.: Записать число и классная работа в тетрадях.
У.: Примеры решить в тетрадях.
| 80-70 | 16+14 | 41+9 | 10 – У | |||
| 55+5 | 37+13 | 30+50 | 30 – В | |||
| 98-8 | 40+30 | 63+7 | 50 – Н | |||
| 60 – Р | ||||||
| 70 – Е | ||||||
| 80 – И | ||||||
| 90 – А | ||||||
| УРАВНЕНИЕ | ||||||
Д.: Это пример с окошечком.
Д.: Это буквенное выражение.
У.: Что вы делали в первом случае?
Д.: Подбирали число чтобы запись была верной.
У.: Какое это число?
Д.: 8.
У.: что делали во втором случае?
Д.: вместо буквы подставляли число и вычисляли.
У.: Посмотрите на запись х+4=12
У.: На что оно похожа?
Д.: На пример с окошечком, на буквенное выражение.
У.: Что нам говорит знак =?
Д.: Равенство.
У.: Какое равенство? Все числа в нем известны?
Д.: Нет.
У.: Что неизвестно?
Д.: Первое число.
У.: как оно обозначено?
Д.: Латинской буквой.
У.: Если оно неизвестно, перед нами какая встает задача?
Д.: Найти, узнать какое это число.
У.: Найдите это число, чтобы равенство было верным.
Д.: Это число 8 (8+4=12).
У.: Что мы с вами сейчас сделали?
Вы решили уравнение.
У.: Сделаем вывод:
Уравнение – это ……(показать знак =)
Д.: Равенство.
У.: Которое содержит что? (показать на х)
Д.: Неизвестное число.
У.: Что надо сделать с неизвестным числом?
Д.: Его найти.
У.: Как обозначается неизвестное число?
Д.: Латинской буквой.
У.: Кто сможет сказать, что такое уравнение?
Д.: Уравнение – это равенство, которое содержит неизвестное число.
У.: Что значит решить уравнение?
Плакат на доске: Уравнение – это равенство, которое содержит неизвестное число. Решить уравнение – найти такое число, чтобы равенство было верным.
У.: Число, которое мы находим в уравнении х – называется корнем уравнения.
У.: Решить уравнение можно с помощью подбора ( или зная взаимосвязь компонентов при сложении и вычитании)
IV. Физкультминутка (на дыхание).
Раз, два, три, четыре, пять!
Все умеем мы считать
Отдыхать умеем тоже –
Руки за спину положим
Голову поднимем выше
И легко-легко подышим.
V. Первичное закрепление нового материала.
а) У.: Среди данных выражений выбрать нужно уравнение и записать в тетрадь.
Методика работы над изучением уравнений в начальной школе
Методика работы над изучением уравнений в начальной школе
Математика – наука, которая нужна каждому человеку. В каждой области знания, в любой профессии нужна помощь математики.
Основная часть нашей жизни состоит из вычислений и подсчетов. Математика помогает развивать интеллект и находить решения в сложной задаче. Математика учит нас получать и приобретать знания, развивает внимание, логику, ясное мышление, умение делать выводы.
Уже с первого класса дети начинают задаваться вопросами: зачем мы изучаем математику? Чем она пригодиться в жизни?
Роль обучения в решении уравнений в начальной школе достаточно велика и ее сложно переоценить.
Во-первых, знания, умения и навыки, приобретенные школьниками при решении уравнений в начальной школе, помогут им в изучении математических дисциплин и будут способствовать скорейшему усвоению нового материала.
Во-вторых, обучение решению уравнений способствует развитию мышления у школьников, которое так необходимо не только при изучении стереометрии и геометрии в целом, но и в обыденной жизни, когда получить ответ на поставленный вопрос можно только владея навыками решения уравнений.
В-третьих, можно так же отметить, что обучение навыкам решения уравнений в начальной школе является своевременным и необходимым, так как именно в этом возрасте учащиеся лучше усваивают полученную от преподавателя информацию и с раннего возраста начинают понимать основные принципы и методики решения более сложных задач, заранее подготавливаясь к изучению высших математических дисциплин.
Основные подходы к обучению решению уравнений:
Раннее ознакомление детей с уравнением и способами его решения (М.И.Моро, М.А.Бантова, И.Э.Аргинская, Л.Г.Петерсон и др.) – с 1-2 класса.
Методика изучения уравнений:
1) Подготовительный
Изучать уравнения дети начинают уже с первого класса, используя в помощь различные фигуры или предметы:
Следующие действия, к которым переходят учащиеся, связаны с нахождением числа в «окошке»:
1. Какие записи верны?
3 + 5 = 8 7 + 2 = 10 10 – 4 = 5
Как изменить результат, чтобы записи стали верными??
3. Среди чисел, записанных справа, подчеркните то число, при подстановке которого в окошко, получится верное равенство.
2) Введение понятия «уравнение»
3) Формирование умения решать уравнения
Способы решения уравнений:
В курсе математики УМК «Школа России»:
По программе И.И.Аргинской (система обучения Л.В.Занкова):
При проверке уравнения следует показать учащимся, что результат, полученный в левой части уравнения, нужно сравнить со значением в правой части. Необходимо добиться осознанного выполнения проверки.
4) Формирование умения решать задачи с помощью уравнений.
Процесс решения текстовой задачи с помощью уравнений состоит из следующих этапов:
1. Восприятие текста задачи и первичный анализ ее содержания.
выделение неизвестных чисел;
выбор неизвестного, которое целесообразно обозначить буквой;
переформулировка текста задачи с принятыми обозначениями;
запись полученного текста.
3. Составление уравнения, его решение, проверка, перевод найденного значения переменной на язык текста задачи.
4. Проверка решения задачи любым известным способом.
5. Формулирование ответа на вопрос задачи.
Виды упражнений, направленные на обучение младших школьников решению уравнений в учебниках математики УМК «Школа России»:
Вид упражнения
Пример задания
Задания с «окошками» и пропусками чисел
2) Какие числа пропущены?
3) Заполни пропуски так, чтобы равенства стали верными.
Нахождение уравнений среди других математических записей
1) Найди среди следующих записей уравнения, выпиши их и реши.
30+х>40 45-5=40 60+х=90 80-х 38-8
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Алгебра. 7 класс
Конспект урока
Решение линейных уравнений с одним неизвестным
Перечень рассматриваемых вопросов:
• Решение линейных уравнений.
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.
Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.
Свободный член – член уравнения, не содержащий неизвестного.
Решить уравнение – значит найти все его корни или установить, что их нет.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.

Корнем уравнения называют, такое значение переменной, при которой уравнение преобразуется в верное числовое равенство.
А что же означает решить уравнение?
Решить уравнение означает найти все его корни или доказать, что корней нет.
Давайте попробуем сформулировать теперь, как решать линейные уравнения и подумаем, а какие у нас могут быть случаи?
Решение линейного уравнения – это приведение его путем тождественных преобразований к стандартному виду.
Давайте решим уравнение:

А теперь давайте решим другое уравнение:


0 = 0, следовательно, уравнение имеет бесконечное множество корней.
Отсюда можно сделать вывод, что возможные варианты решения уравнения, зависят от того, какие значения принимает свободный член и коэффициент при переменной.
При решении уравнения вида возможны следующие три случая:

Да, конечно можно. Для этого нужно подставить в уравнение вместо переменной это число, если после упрощения, мы получаем верное равенство, то данное число будет являться корнем уравнения.
Давайте проверим, так ли это. Узнаем, является ли число






Алгебра. 7 класс
Конспект урока
Уравнения первой степени с одним неизвестным. Линейные уравнения с одним неизвестным
Перечень рассматриваемых вопросов:
Решение линейных уравнений.
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.
Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.
Свободный член – член уравнения, не содержащий неизвестного.
Решить уравнение – значит найти все его корни или установить, что их нет.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.
Линейное уравнение – уравнение вида ax = b, где x – переменная, a, b – некоторые числа.
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Давайте посмотрим на 2 уравнения: 10x = 36 и 3x 2 = 2
Можем ли мы сказать, что оба уравнения являются линейными уравнениями первой степени?
Конечно, нет. Хотя, по определению линейных уравнений, оба уравнения подходят, у второго уравнения переменная входит в него во второй степени, а это противоречит отличительной особенности линейного уравнения первой степени.
Определение: Уравнение вида ax = b, где – x переменная, a, b – некоторые числа, называется линейным уравнением с одной переменной.
А что означает решить уравнение?
Решить уравнение – означает найти все его корни или доказать, что корней нет.
Линейными уравнениями называются не только уравнения вида ax + b = 0, но и любые уравнения, которые преобразованиями и упрощениями сводятся к этому виду.
Давайте подумаем, является ли уравнение 2(5x + 4) = 2x – 16 – линейным уравнением первой степени? Нет, так как оно не записано в виде ax = b. Можно ли привести его к такому виду?
Попробуем это сделать. Переменная x входит в это уравнение первой степени. Все такие уравнения можно преобразовать в вид ax + b = 0 с помощью тождественных преобразований. Для этого раскроем скобки в левой части уравнения, воспользовавшись распределительным законом умножения.
Вычтем из правой и левой частей уравнения 2x и 8.
Затем приведём подобные слагаемые в левой и правой частях уравнения и получим уравнение стандартного вида.
А как же проверить, является ли число корнем уравнения, не решая его?
В таком случае, нам достаточно подставить значение переменной в уравнение и проверить, выполняется равенство или нет.
Чтобы узнать, является ли число корнем уравнения, нужно:
— Подставить вместо переменной числовое значение.
— Посмотреть, получилось верное равенство или нет.
Если верное, то число является корнем уравнения, в противном случае – нет.
Чётко распознать линейное уравнение можно в некоторых случаях. Скажем, если перед нами уравнения, в которых есть только неизвестные в первой степени и числа.
Приведём это уравнение к стандартному виду. В левой части раскроем скобки:
Линейное уравнение имеет вид:
Задание 1. Какое значение переменной удовлетворяет уравнению 4x – 2 = 14?
Для того чтобы определить, какое из значений удовлетворяет уравнению, нужно подставить вместо переменной соответствующее значение и проверить, получается ли истинное равенство. Соответственно, при истинности, значение переменной будет удовлетворять условию.
При x = 0 получаем: 4 · 0 – 2 = 14
–2 = 14 – ложь. Следовательно, x = 0 не удовлетворяет решению уравнения.
При x = 2,5 получаем: 4 · 2,5 – 2 = 14
3 = 14 – ложь. Следовательно, x = 2,5 не удовлетворяет решению уравнения.
При x = 4 получаем: 4 · 4 – 2 = 14
14 = 14 – истина. Следовательно, x = 4 удовлетворяет решению уравнения.
При x = 0,1 получаем: 4 · 0,1 – 2 = 14
–1,6 = 14 – ложь. Следовательно, x = 0,1 не удовлетворяет решению уравнения.
Задание 2. Уравнение 2(2x – 3) = 2x + 16 надо привести к стандартному виду.
Для того чтобы определить, какое из значений является верным приведением уравнения к стандартному виду, нужно просто привести уравнение к стандартному виду.
2(2x – 3) = 2x + 16 – раскроем скобки, умножив число на разность;
4x – 6 = 2x + 16 – преобразуем уравнение, перенеся слагаемые, содержащие переменные в левую часть уравнения, а числа в правую, меняя при этом знак на противоположный;
4x – 2x = 16 – 6 – упростим выражение, приведя подобные слагаемые;
2x = 22 – полученное уравнение приведено к стандартному виду ax = b, где a = 1, b = 22
Начальные классы. Уравнения.
С уравнениями ученики знакомятся в 1 классе. Сначала решают примеры с окошком: выполняют действия с числами и задания на нахождение неизвестного числа, например было равенство:
И одно число решили спрятать:
Нам нужно догадаться, что за число спрятали?
Здесь прекрасно видно, чтобы найти неизвестное число, нужно из 9 — 2
Искомое число – 7.
В нашем равенстве – искомое число называют неизвестным числом.
А равенство, в котором одно число стало неизвестным, называется УРАВНЕНИЕМ.
Никто из вас никогда не видел, чтобы уравнения делали с «окошком». Это неудобно. Гораздо проще неизвестное обозначать буквами.
Неизвестное число обозначают маленькими латинскими буквами
или любой другой буквой.
И этому числу дают имя – корень уравнения.
Давайте посмотрим записи:
8+х
8+х>5
8+х =10
Только третья запись — уравнение. Потому что здесь есть неизвестное число и знак =.
Нам необходимо узнать это число.
Найти все значения х, при котором равенство будет верным — значит, решить уравнение, т.е. найти его корень.
При решении уравнения учитываем взаимосвязи между целым и частью:
— чтобы найти целое, надо сложить части;
— чтобы найти часть, надо из целого вычесть другую часть.
Если вы хотите более подробно узнать, как связаны целое и части, читайте тут.
Решение записывается так:
Корень пишем на следующей строке и подчеркиваем прямой линией.
Корень уравнения = 7, следовательно, наше уравнение решено.
Нам обязательно нужно проверить правильно мы нашли корень уравнения или нет.
Уравнение без проверки – это не уравнение.
Итак, в нашем уравнении корень –7, мы его подчеркнули, а теперь сделаем проверку. Для этого мы переписываем первую строку уравнения, но вместо неизвестного поставим значение корня.
Теперь: знак = пишем под знаком =. Число, записанное справа от знака равно: 9 – переписываем. Выражение, которое находится слева от знака равно: 7 + 2 – считаем. Получится 9. Это число 9 записываем слева от знака =.
Читаем выражение: 9 = 9. Значит, уравнение решили правильно.
Решим еще одно уравнение:

Ученикам начальной школы нужно обязательно овладеть математической речью. Для этого нужно знать, как называются компоненты при различных действиях, и как находится неизвестный компонент:
Если из суммы вычесть одно из слагаемых, то получится другое слагаемое.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 64