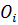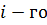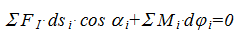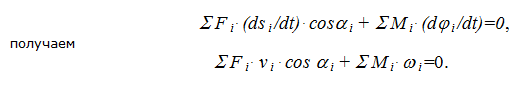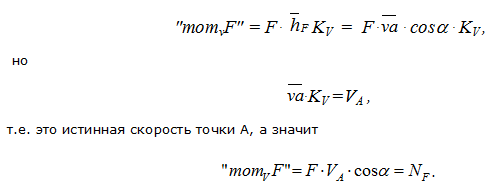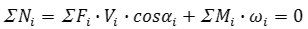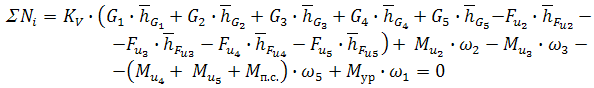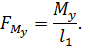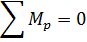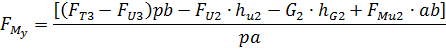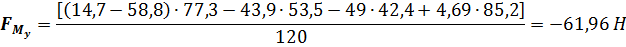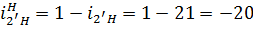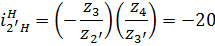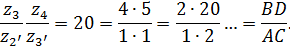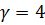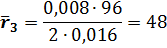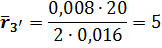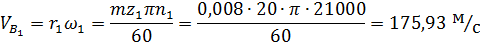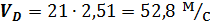Что такое уравновешивающий момент

iSopromat.ru

Определять уравновешивающую силу или момент методом Н.Е. Жуковского можно в случаях, когда требуется найти только неизвестную внешнюю силу без определения реакций в кинематических парах, не прибегая к последовательному силовому расчету всего механизма.

Метод основан на принципе возможных перемещений – если система находится в равновесии, то сумма работ внешних сил и моментов на малых возможных перемещениях равна нулю ( ∑ Ai = 0). Так как с помощью сил инерции (по принципу Даламбера) механизм приведен в состояние равновесия, то в данном случае принцип возможных перемещений применим.

Перейдем к конкретному мгновенному положению механизма, разделив все члены на бесконечно малый промежуток времени (dt), за который происходят указанные малые перемещения:

Таким образом, уравнение работ трансформируется в уравнение мгновенных мощностей и принцип возможных перемещений в применении к механизму можно сформулировать следующим образом – если механизм находится в равновесии, то сумма мгновенных мощностей всех внешних сил и моментов, приложенных к звеньям механизма, равна нулю.

Жуковским Н.Е. был предложен метод составления этого уравнения с использованием плана скоростей (рисунок 19).

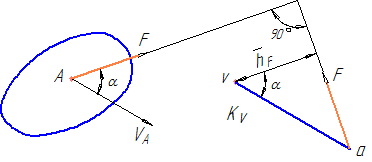
На рисунке 19 изображено некоторое звено, в точке А которого приложена сила F. Скорость V_A этой точки изображается на плане скоростей вектором va в масштабе K_V.

Перенесем силу F в точку «а» плана скоростей, повернув на 90° (в любую сторону). Возьмем формально момент этой повернутой силы относительно полюса плана скоростей:

В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.

Таким образом для составления уравнения Жуковского прикладывают все силы, действующие на звенья механизма (включая силы инерции), в соответствующие точки плана скоростей, предварительно повернув их на 90°. Взяв формально сумму моментов этих повернутых сил относительно полюса плана скоростей, фактически получают уравнение развиваемых ими мощностей.

К полученному уравнению добавляют мощности, развиваемые моментами (включая моменты сил инерции).

В уравнение Жуковского мощности должны входить с соответствующими знаками (см. рисунок 16 ). В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.

Примечание: для составления уравнения Жуковского можно на повернутый (на 90°) план скоростей прикладывать силы в своем истинном направлении.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Большая Энциклопедия Нефти и Газа

Уравновешивающий момент

Уравновешивающий момент зависит от упругости пружин, если они используются, или от дополнительных сопротивлений, если момент создается магнитом, как, например, на фиг. [1]

Уравновешивающий момент на звене создается непосредственно двигателем, если звено / соединено с ротором электродвигателя, или уравновешивающей силой, точка приложения которой ] определяется структурой передаточного механизма. [2]

Уравновешивающий момент для выбранного положения механизма производит положительную работу, потому что он действует в направлении, совпадающем с направлением вращения начального звена. [3]

Определяем уравновешивающий момент по методу Жуковского, для чего строим повернутый план скоростей. [5]

ДНОП уравновешивающий момент создается закручиванием упругой нити, а показания В считываются с лимбов, связанных с передней рукояткой. [6]

Иногда уравновешивающий момент изменяется перемещением груза в грузовом уравновешивателе. Перемещение производится двигателем по сигналу датчика угла поворота плеча робота. При этом можно осуществлять и динамическую балансировку, задавая соответствующим образом закон перемещения груза. [8]

Под уравновешивающим моментом ( или силой), приложенным к ведущему звену, понимают тот момент, который должен быть приложен со стороны двигателя к механизму, чтобы при данном движении механизма преодолевались сопротивления всех внешних сил, действующих на механизм. [10]

Требуется определить уравновешивающий момент М и давления в кинематических парах. Планы скоростей и ускорений рассматриваемого механизма построены на рис. 73, б, в. В технических расчетах кривошип ОА считают уравновешенным, и потому в этом случае сила инерции Ри его равна нулю. [11]

Так, уравновешивающий момент равняется необходимому вращающему моменту, который должен быть приложен, чтобы механизм двигался с заданной скоростью, преодолевая заданную нагрузку. Из формулировки видно, что речь идет об условной или фиктивной величине момента. [12]

Величина каждого уравновешивающего момента составляет долю неуравновешенного момента М2, определяемую коэффициентом распределения. [13]

Коэффициенты распределения уравновешивающих моментов между стержнями каждого узла определяются с учетом коэффициентов жесткости изгибаемых и скручиваемых стержней. [14]

Одновременно с уравновешивающими моментами на противоположных защемленных концах стержней, сходящихся в узле 3, а также и у защемленных концов всех стоек возникнут вторичные моменты защемления, равные частным от деления уравновешивающих моментов на соответствующие им коэффициенты переноса. [15]

Источник

iSopromat.ru

Рассмотрим порядок расчета уравновешивающего момента методом Н.Е. Жуковского.

Физический смысл уравнения Жуковского – сумма мгновенных мощностей, развиваемых силами и моментами, действующими на звенья механизма, равна нулю.

Для его составления прикладываем все силы в соответствующие точки плана скоростей, предварительно повернув их на 90 градусов (силы можно поворачивать в любую сторону, но все силы надо поворачивать в одну сторону – по часовой стрелке или против часовой стрелки).

Взяв, формально, сумму моментов этих повернутых сил относительно полюса плана скоростей, фактически получаем уравнение развиваемых ими мощностей. К полученному уравнению добавляем мощности, развиваемые моментами. При составлении уравнения Жуковского Н.Е. учитываем знак мощности, развиваемой данной силой или моментом:

Примечание: для составления уравнения Жуковского Н.Е. можно поворачивать на 90° план скоростей, прикладывая к нему силы в истинном направлении.

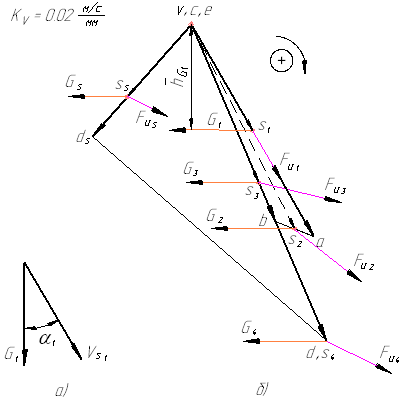
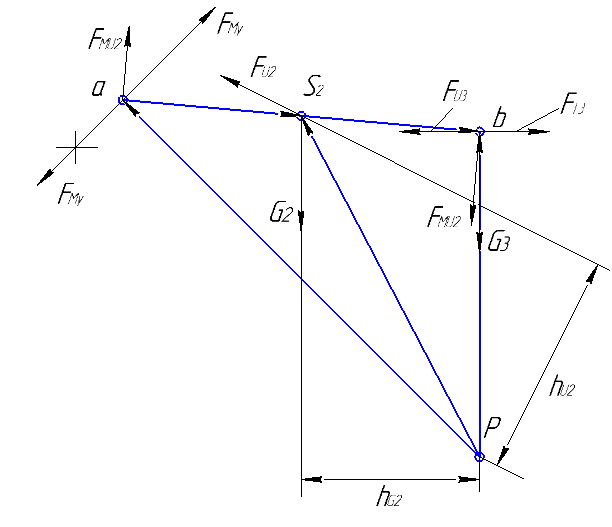
Рисунок 11 – Применение метода Н.Е. Жуковского для определения уравновешивающего момента

На рисунке 11 показана реализация данного метода на примере механизма, силовой расчет которого рассмотрен выше. В данном примере все силы, действующие на звенья механизма, повернуты по часовой стрелке и приложены в соответствующие точки плана скоростей, которые определяются методом подобия. Сначала определяем знак мощности какой-либо из сил, например, силы веса первого звена G₁.

Истинное направление силы веса и скорости точки его приложения в данном случае составляют острый угол (рисунок 11а), поэтому данная сила развивает положительную мощность и в уравнение Н.Е. Жуковского эта мощность должна войти со знаком «плюс». Если рассматривать план скоростей как жесткий рычаг, то в повернутом состоянии сила G₁ вращает его относительно полюса по часовой стрелке (рисунок 11б).

Таким образом, мощности сил, вращающих план скоростей по часовой стрелке, войдут в уравнение Н,Е. Жуковского со знаком «плюс», вращающие план против часовой стрелки – со знаком «минус».

Для определения знака мощности, развиваемой моментом, надо просто сравнить направление данного момента и угловой скорости звена, к которому он приложен (рисунки 5, 8, 9). При совпадении направлений момента и угловой скорости их произведение в уравнение входит со знаком «плюс», при разных направлениях – со знаком «минус».

Для приведенного примера (рисунок 11) уравнение Н.Е.Жуковского принимает следующий вид:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Определение уравновешивающего момента с помощью рычага Жуковского

Рычаг Жуковского является графической интерпретацией метода возможных перемещений.

Н.Е.Жуковский показал, что если векторы всех сил, приложенных к различным точкам звеньев мезанизма, перенести параллельно самим себе в одноименные точки повернутого на 90 0 плана скоростей, приняв фигуру плана за жесткий рычак, то момент каждой силы относительно полюса плана скоростей будет пропорционален ее мощности, а сумма моментов всех указанных сил будет равна нулю. При этом все моменты, в том числе и уравновешивающий, должен быть заменены парами сил.

Пара сил 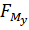, заменяющая уравновешивающий момент, будет

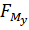
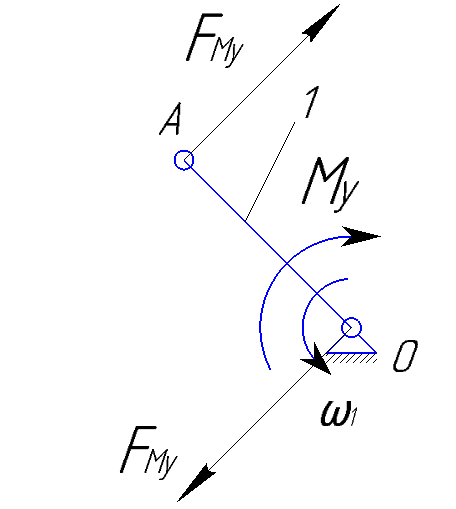
Рычаг Жуковского представлен на рис.3.4, а. План скоростей здесь повернут на 90 0 по часовой стерлки. Сила произвольно направлена вниз от точки а плана.

Рис.3.4. Схема первичного механизма и рычаг Жуковского

Сумма моменто сил относительно полюса плана сил р имеет вид

В этом выражении плечи сил определяются из чертежа путем замера.

Как видоно из формулы, величина силы 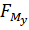не зависит от масштаба построения рычага Жуковского.

Численное значение силы от уравновешивающего момента для рассматриваемого примера равно

Для определения уравновешивающего момента необходимо полученную силу пренести параллельно самой себе из раычага Жусовского в точку А первичного механизма (рис.3.4,б). Тогда уравновешивающий момент будет положительным и иметь вид

Его величина для рассматриваемого примера

Для примера расчета получены следующие разультаты.

1. Вычислены кинематические характеристики ведомых звеньев механизма, позволяющие сделать вывод с рациональности его параметров.

2. Получены силы и моменты сил, действующие на звенья механизма, позволяющие произветси их расчет на прочность при конструировании.

3. Выявлено влияние сил трения в кинематических парах механизма, позволяющее оценить его КПД.

4. Вычислен уравновешивающий момент, позволяющий щценить потребную мощность для его привода. Для приведенного примера без учета потерь на трение она будет

При подборе электродвигателя следует учесть КПД механизма.

1. Артоболевский И.И. Теория механизма и машин.-М.: Наука, 1988. – 640с.

2. Иосилевич Г.Б., Строганов Г.Б., Маслов Г.С. Прикладная механика. – М.: Высшая школа, 1989. – 351 с.

3. Фралов К.В., Попов С.А. и др. Теория механизмов и машин. – М.: Высшая школа, 1987. – 496 с.

Часть 2

Анализ и синтез планетарного редуктора

Исходные данные для расчета (задание 1047):

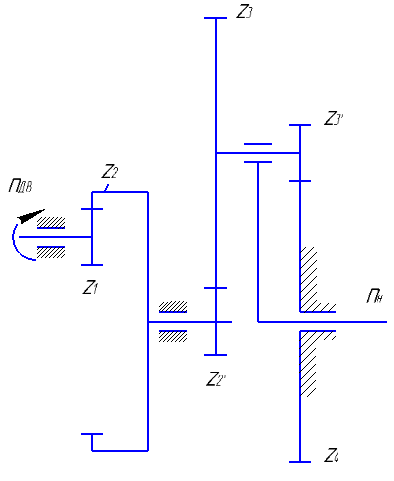
1.Стуктурная схема комбинированного редуктора (рис.1а)

2. Число оборотов на входе редуктора =12000 об./мин.

3. Число обротов навыходе редуктора 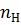=250 об./мин.

4.Модуль зубчатых колес передачи m = 8 мм. =0,008 м.

Необходимо выполнить синтез данного планетарного редуктора (найти все z_i) беспечивающие работоспособность и заданные передаточные отношения.

Решение. 1.Разбивка общего передаточного отношения по ступеням (первая ступень – рядовая i₁₂ и вторая ступень – планетарная i_2’H):

Обычно для такой цилиндрической зубчатой передачи рекомендуется принимать 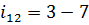. Для планетарной ступени .

Принимаем тогда

2.Подбор чисел зубьев планетарного механизма. Подберём числа зубьев планетарной ступени, обеспечивающие 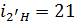и соосность осей планетарной ступени по приведенным формулам:

Одновременно возможные варианты значений A,B,C и D:

Рассмотрим два варианта подбора чисел зубьев зубчатых колес.

С помощью выбора соответствующего 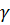удовлетворяем рекомендации по выбору

Принимаем для внешнего зацепления для внутреннего – Принимаем также

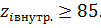
Принимаем

Из двух вариантов вибираем тот, который имеет меньшие габариты, т.е. меньшую сумму зубьев колес, определяющих габариты.

Выбираем первый вариант.

Определяем числов зубьев колес 1 и 2 с помощью соотношения

Принимаем Тогда

3. Определение числа сателлитов. Из условия соседства определим возможное число сателлитов.

Число сателлитов будет

Отсюда .

4. Проверка возможности сборки. Условие сборки имеет вид:

При т.е. при любом целом p число C будет целом числом, т.е сборка возможно.

5.Кинематический расчет редуктора графоаналитическим метдом. Расчет редуктора графоаналитическим методом выполняется в следующей последовательности.

1.Выбор масштабного коэффициента 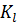для построение плана механизма.

2. Построение плана механизма(рис 15,а).

Рис. 15 Кинематический анализ механизма графическим методом

3. Выбор масштабного коэффициента 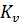для построения графика линейных скоростей.

4. Построение графика линейных скоростей (рис. 15,б).

5. Выбор масштабного коэффициента для построения плана чисел оборотов

6.Построение плана чисел оборотов (рис. 15,в).

Построение плана зубчатого механизма необходимо начать с определения масштабного коэффициента из равенства:

где m-модуль зацепления; число зубьев первого колеса; — длина отрезка, изображающего на плане механизма радиус первого зубчатого колеса.

Размеры других отрезков, изображающих радиусы колес, равны

После построения плана редуктора обозначим на чертеже точки кнтакта колес, оси сателлитов и колес (A, B, C, D,E и F).

Масштабный коэффициент для построения графика линейных скоростей определим из соотношения

где -скорость точки первого зубчатого колеса; – длина отрезка, изображающего на графике скорость точки .

Скорость точки первого колеса равна

где -число оборотов первого зубчатого колеса .

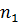
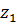
Графики линейных скоростей точек зубчатых колес представлены на рис.15,б.

Линия расперделения скоростей каждого колеса строится по двум точкам, скорости которых известны. Так, для первого звена известна скорость точки величина которой определяется по формуле (5)

а скорость оси вращения колеса равна нулю. По этим двум точкам строится график распределения окуржных скоростей точек первого звена .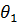

Соединяя точку D’’ с точкой F’ получаем линию 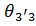график окружных скоростей точек звеньев 3 и 3’ относительно водила H.

План угловых скоростей зубчаты колес редуктора приведен на рис.15,в.

Масштабный кожффициент для построения плана чисел оборотов определим из равенства

Где 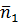— размер отрезка, изображающего на плане чисел оборотов первого звена; принимаем

Построение плана чисел обротов можно начать с отложения на горизонтальной линии отрезка соответствующего числу обротов первого звена. Далее из конца этого отрезка (точки 1) проводим линию, параллельную , до пересечения ее с вертикальной линией, провденной из начала отрезка (из точки O). Получим точку пересечения линии с вертикальной осью. Из этой точки проводим линии, параллельные линиям распределения окружных скоростей точек звеньев на графике линейных скоростей. Отрезок пропорционален числу оборотов первого зубчатого колеса, отрезок – числу оборотов второго колеса и т.д. Числа оборотов колес можно определить по формуле

где — длина отрезка, соответствующего числу оборотов звена на плане чисел оборотов.

Источник