что такое световой конус
Световой конус
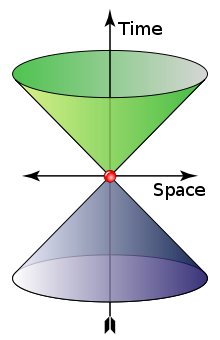
Светово́й ко́нус (изотропный конус, нулевой конус) — гиперповерхность в пространстве-времени (чаще всего в пространстве Минковского), ограничивающая области будущего и прошлого относительно заданного события.
Содержание
Определение
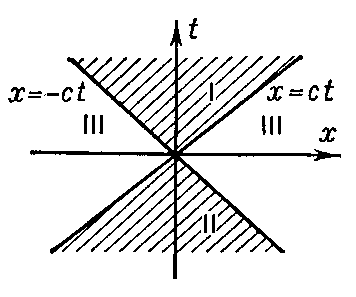
Световой конус можно определить как множество всех точек, для которых интервал, отделяющий их от данного события (вершины светового конуса), светоподобен (то есть равен нулю). Вершина разделяет поверхность светового конуса на две части. Одна часть поверхности лежит в области будущего по отношению к вершине и содержит все события, которых может достичь световой сигнал из вершины; можно представлять, что в событии-вершине произошла мгновенная вспышка. Другая часть содержит все события в прошлом, такие, что испущенный из них световой сигнал может достичь вершины. Ось светового конуса в пространстве Минковского в любой инерциальной системе отсчёта совпадает с проходящей через вершину мировой линией частицы, неподвижной в данной системе отсчёта.
Поскольку никакой сигнал не может распространяться быстрее света, световой конус имеет прямое отношение к причинно-следственной структуре пространства, а именно, он разделяет всё пространство-время на три части по отношению к вершине: область абсолютного прошлого (конус прошлого; все события, которые могли повлиять на событие в вершине), область абсолютного будущего (конус будущего; все события, на которые влияет событие в вершине конуса) и область абсолютно удалённого (события, отделённые от вершины пространственноподобным интервалом, то есть не связанные с вершиной причинно-следственными связями). Уравнение светового конуса с вершиной в начале отсчёта зависит от пространства-времени, и имеет особенно простой вид в пространстве Минковского:

инвариантный по отношению к преобразованиям Лоренца. Преобразования Лоренца, сохраняющие порядок времени, полностью сохраняют и описанное деление пространства-времени.
Световой конус и 4-скорость
Безмассовые же частицы, напротив, имеют 4-импульсы, лежащие на самом световом конусе (его поверхности). Понятие 4-скорости для таких частиц определено только с точностью до умножения на положительное число (её «длина» равна 0).
Физический смысл пространства-времени
В предыдущей заметке мы уже частично коснулись геометрического смысла рассматриваемого нами пространства-времени. Давайте теперь посмотрим, как оно соотносится с нашей реальностью.
Интервалы времени и расстояния
Все времениподобные интервалы описывают просто интервалы времени. Пространственноподобные отрезки соответствуют пространственным расстояниям.
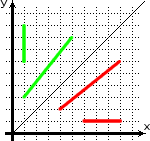
Давайте снова посмотрим на рисунок из предыдущей заметки:
Зелёные отрезки отвечают интервалам времени (по три секунды, так как длина обоих равна трём).
Красные отрезки отвечают интервалам расстояния, протяжённостью «три» в наших единицах. Напомню, что у нас единица расстояния равна расстоянию, которое проходит свет за одну секунду. То есть расстояние, равное «трём» равно 3с, что составляет 3·299,792,458 = 899,377,374 метров (в 70 раз больше диаметра земли).
Световой конус
Одним из важнейших объектов пространства-времени является световой конус. Что это такое?
Давайте на время представим, трёхмерное пространство-время, где два измерения — это наши обычные длина и ширина, а по вертикали отложено время. Как в такой системе будет выглядеть процесс распространения света?
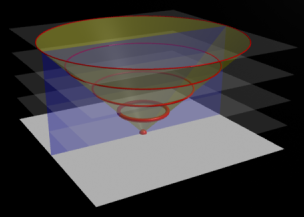
В нулевой момент времени, когда произошла вспышка, наше пространство изображено в виде белой горизонтальной плоскости:
Последующие моменты времени показаны прозрачными белыми плоскостями. Чем больше прошло времени от вспышки, тем дальше уходит световая волна (красные круги), а все точки, которые проходит волна в пространстве-времени, образуют конус (показан жёлтым).
В двухмерном пространстве-времени, показанном на рисунке синей плоскостью, свет вычерчивает две прямые (или, точнее, полупрямые). Причём, если мы будем придерживаться введённых ранее единиц измерения, то эти линии будут располагаться под углом 45 градусов. Это и есть точки отстоящие от начала координат на 0 единиц. А в начале координат, как вы помните, и произошла вспышка. То есть в терминах пространства-времени фотоны (частицы света) неподвижны, они не проходят никакого расстояния и не ощущают хода времени, оно для них просто стоит на месте.
Здесь надо понимать, что мы говорим о времени фотона, то есть о времени, которое показывают часы, прикреплённые к фотону. То же самое касается и расстояния. Кроме того, фотон покоится именно в терминах пространства-времени. Это не значит, что он проходит нулевое расстояние или нулевое время. Это значит только, что интервал между любыми двумя точками, через которые проходил фотон равен нулю.
Для вас, как для наблюдателя, может казаться, что фотон вполне успешно преодолевает не равные нулю расстояния и существует продолжительное время. Но мы вскоре увидим, что измеряемые нами промежутки времени и пространства зависят от нашей скорости и не являются универсальными характеристиками движения, каковой является пространственно-временной интервал.
Мировые линии и отсчёт времени
Сперва я хочу сказать несколько важных слов о том, как я буду выбирать и именовать оси и направления. Я не буду изменять традиции и согласно предыдущему рисунку буду располагать ось времени вертикально, а ось пространственных координат — горизонтально. Но пусть это не вводит вас в заблуждение! Горизонтальная ось никак не совпадает с пространством. Как мы скоро увидим, нет единого пространства, универсального для всех наблюдателей. То же самое касается и времени. Что бы не подвергать вас излишнему соблазну, я не буду подписывать оси. Перпендикулярные оси вообще имеют смысл только для покоящегося наблюдателя и не чуть не лучше и не хуже бесконечного числа других осей, задающих пространство и время всех возможных наблюдателей.
Как известно, никакое тело и никакой сигнал не может двигаться быстрее света, поэтому все мировые линии движущихся тел всегда лежат внутри светового конуса.
При этом пройденные интервалы (в терминах пространства-времени) являются времениподобными и имеют смысл времени, прошедшего для движущегося наблюдателя.
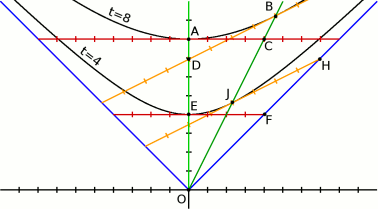
На следующем рисунке изображён световой конус (два синих луча с наклоном в 45 градусов) и линии точек, удалённых от начала координат на 4 и 8 секунд (две кривые, обозначенные «t=4» и «t=8»).
На этом же рисунке изображены две мировые линии. Ярко-зелёная (проходящая через точки O, E, D, A) — это линия покоящегося наблюдателя. Тёмно-зелёная (проходящая через точки O, J, C, B) — наблюдатель, движущийся со скоростью c/2, или в наших единицах — 1/2.
Часы покоящегося наблюдателя покажут 4 секунды в точке E, часы движущегося наблюдателя покажут тоже время в точке J. И точка E, и точка J лежат на линии «t=4» и в терминах пространства-времени равноудалены от точки старта наблюдателей O.
Аналогично часы обоих наблюдателей покажут 8 секунд в точках A и B, лежащих на линии «t=8».
Одновременные пространства
Одновременное пространство наблюдателя — это то пространство, которое по мнению наблюдателя существует в данный момент.
Строго говоря, это то пространство (или те точки пространства-времени), все часы в котором сохраняют синхронность с часами наблюдателя. Оттолкнувшись от этого определения можно изложить доказательства более строго, но так как я не буду здесь приводить строгих доказательств, то и строгое определение оказывается излишним.
Естественно для разных наблюдателей эти пространства будут разными, они являются касательными к линиям равного времени.
Я бы не хотел здесь подробно рассматривать, почему именно касательными. Заинтересовавшиеся читатели могут найти объяснение в специальной литературе. Однако это утверждение можно легко подкрепить простыми соображениями.
Наблюдатель всегда может найти в своём одновременном пространстве точки, которые находятся рядом с ним. Эти точки, конечно будут лежать на кривых равного времени. Оттолкнувшись от этого направления (которое задаёт направление касательной к кривым равного времени) можно построить всё протяжённое одновременное пространство.
Одновременные пространства наших двух наблюдателей в моменты «t=4» и «t=8» показаны на рисунке красными и оранжевыми линиями.
Из построения видно, что так как угол наклона мировых линий всегда больше 45 градусов, то угол наклона одновременных пространств всегда меньше 45 градусов. То есть одновременные пространства всегда пространственноподобны.
На пространственных линиях на рисунке показаны единичные интервалы (в терминах пространства времени).
Специальная теория относительности помогла компьютеру предсказать будущее
A. Vlontzos et al. / arXiv.org
Ежедневно, иногда сами того не замечая, мы пытаемся предсказать, как будут развиваться события вокруг нас. Например, если у двигающегося перед нами автомобиля включен сигнал указателя поворота, то можно предполагать, что он с определенной вероятностью совершит маневр в соответствующем направлении. Однако, автомобиль также может продолжить движение без изменений, остановиться или повернуть в противоположную указываемому направлению сторону. Эти события вероятны в большей или меньшей степени, и мы можем ожидать их, основываясь на опыте взаимодействия с миром и интуитивном понимании законов физики и причинно-следственных связей. С другой стороны, вряд ли мы будем всерьез рассматривать возможность того, что автомобиль внезапно исчезнет и вместо него на дороге вдруг появится динозавр.
В отличие от людей, у компьютеров нет интуитивного понимания причинно-следственных связей, поэтому прогнозирование будущих событий для них оказывается непростой задачей. При этом во многих областях, где сегодня происходит интенсивное внедрение систем с машинным обучением, появление такой способности могло бы повысить уровень безопасности. Например, автомобиль под управлением автопилота мог бы спрогнозировать и оценить вероятность того, что стоящий у дороги ребенок может внезапно выбежать на проезжую часть.
Существующие подходы к решению задачи предсказания будущего в машинном обучении сводятся, например, к тренировке моделей на последовательностях кадров видео. Таким способом алгоритм обучают выявлять закономерности в событиях, которые в дальнейшем можно использовать для того, чтобы сгенерировать новые, ранее не существовавшие кадры, продолжающие эту последовательность. Например, можно показать программе последовательность кадров с двигающимся человеком, а затем попросить ее сгенерировать следующие несколько кадров, которые бы продолжили исходную последовательность. Однако у подходов, использующих серии и последовательности кадров, есть склонность быстро накапливать ошибки с увеличением числа сгенерированных кадров.
Исследователи под руководством Атанасиоса Влонцоса (Athanasios Vlontzos) из Имперского колледжа Лондона использовали иной подход. Они разработали алгоритм на основе фундаментальных концепций из специальной теории относительности (СТО), таких как пространство-время и световые конусы.
В СТО пространство-время (или пространство Минковского) представляет собой объединение трехмерного евклидова пространства с четвертым временны́м измерением. В таком пространстве каждому событию можно сопоставить точку, пространственные координаты которой описывают место, где событие произошло, а временна́я координата — момент времени, когда оно случилось.
Ограничение на максимально достижимую скорость распространения сигналов (в СТО это скорость света) позволяет выделить в пространстве-времени область, называемую световым конусом, с центром в исходном событии. Множество точек внутри выделенной области будет связано с исходным событием причинно-следственными связями. Так, в конусе будущего, лежащем выше вершины (исходное событие) будут расположены все точки, на которые исходное событие может повлиять, а в нижнем конусе прошлого, — события, которые могли повлиять на рассматриваемое событие в вершине. При этом точки, находящиеся за пределами светового конуса, не связаны причинно-следственными связями с исходным событием.
пересечение световых конусов
A. Vlontzos et al. / arXiv.org
Разработчики использовали эту концепцию для того, чтобы ограничить варианты возможных новых кадров, генерируемых их алгоритмом, такими, которые близки по содержанию к исходному изображению и отбросить изображения, сильно отличающиеся от него. В качестве основы для алгоритма была выбрана разновидность популярного метода для обучения генеративных моделей — вариационный автокодировщик Пуанкаре. Подаваемые на вход изображения преобразуются энкодером в представление в скрытом пространстве, которое обладает свойствами пространства Минковского с восемью пространственными и одним временным измерениями. Такая размерность пространства была выбрана как оптимальная экспериментальным путем. Затем алгоритм строит световые конусы вокруг этих точек и ищет их пересечение для того, чтобы выделить ту часть скрытого пространства, в которой могут находиться будущие (или прошлые, в нижнем конусе) кадры. Похожие по содержанию кадры оказываются недалеко друг от друга. В дальнейшем производя выборку из этого подпространства, можно пытаться предсказывать будущие кадры.
В качестве наборов данных для обучения модели исследователи использовали модифицированный набор moving MNIST, состоящий из небольших фрагментов видео с перемещающимися рукописными цифрами. Каждый фрагмент представляет собой последовательность из 30 кадров. При этом один из них берется из исходного набора данных MNIST, а последующие кадры — случайные непрерывные смещения исходного изображения. Всего было использовано 10000 фрагментов из этого набора. Кроме того, разработчики использовали набор данных KTH action recognition dataset, состоящий из коротких видеоклипов, демонстрирующих движения людей, например ходьбу или взмахи руками. При этом нужно заметить, что кадры в тренировочных наборах воспринимались алгоритмом разрозненно, а не в виде связанных последовательностей или серий.
результаты сгенерированных кадров на основе датасета MNIST, в зависимости от времени
A. Vlontzos et al. / arXiv.org
сгенерированные кадры на основе набора данных KTH action recognition dataset, в зависимости от времени
Замыкая круг времен: наука невозможного
Общая теория относительности не исключает теоретическую возможность попасть в собственное прошлое. Правда, для этого понадобится совсем особая Вселенная, совершенно непохожая на нашу.
Гёделевский мир — это бесконечный цилиндр, заполненный пылевидной гравитирующей материей, которая вращается вокруг центральной оси с постоянной угловой скоростью. Гёдель, как когда-то Эйнштейн, добавил в уравнения ОТО космологическую постоянную, но не положительную, а отрицательную. В результате в его Вселенной появился дополнительный источник тяготения, противодействующий центробежным силам (положительная космологическая постоянная заставляет пространство разлетаться, отрицательная — стягиваться). Это позволило Гёделю построить статичный мир, который не расширяется и не сжимается (и потому, в отличие от фридмановской вселенной, не имеет сингулярности).
Первым решение уравнений ОТО, допускающее путешествие в прошлое, в 1924 году получил венгерский математик Корнелиус Ланцош, вторым стал голландец Виллем ван Стокум. Но в наиболее завершенной форме оно сформулировано в опубликованной в 1949 году статье гениального австрийского математика и логика Курта Гёделя, который тогда был сотрудником принстонского Института фундаментальных исследований. Там он подружился с Эйнштейном, который не раз говорил, что ходит на работу только для того, чтобы возвращаться домой вместе с Гёделем. Эйнштейн и заинтересовал Гёделя математическими проблемами теории тяготения.
В гёделевском космосе возможны путешествия, направленные против течения времени. Выберем стартовую точку, лежащую на мировой оси, и начнем от нее движение по довольно хитрой траектории, которая сначала уведет нас в сторону, а потом вернет на прежнее место. Оказывается, ее можно протянуть так, что момент возврата, определенный по неподвижным часам, будет предшествовать моменту отправления. Правда, для этого придется разгоняться почти до скорости света и к тому же потребовать, чтобы пылевидная материя распределялась в пространстве весьма экзотическим образом. Однако нам не понадобятся сверхсветовые скорости, так что законы природы мы не нарушим!
Избегая парадоксов
А как же быть со знаменитым парадоксом дедушки? Или даже так — что помешает путешественнику во времени прикончить самого себя во младенчестве? Конечно, жизнь в гёделевском пылевом космосе невозможна, но такое возражение звучит не слишком серьезно. Гёдель рассмотрел эту ситуацию с двух сторон. Во-первых, он вычислил, что для гипотетического путешествия в собственное прошлое пришлось бы затратить неправдоподобно большое количество энергии. Во-вторых, он допускал, что существует какой-то еще неизвестный науке принцип запрета, аналогичный квантовомеханическому соотношению неопределенностей, который автоматически исключает такие путешествия.
Световые конусы и путешествия во времени: Геометрия путешествия во времени во вселенной Гёделя
Построим в начальной точке траектории световой конус, трехмерную гиперповерхность в четырехмерном пространстве-времени, образованную световыми лучами. Физическое тело может переместиться из этой точки только внутрь конуса, поскольку лишь туда можно попасть, двигаясь с досветовыми скоростями. Построим такие конусы и в других точках вдоль траектории. Во вселенной Гёделя по мере удаления от оси вращения конусы будут расширяться и наклоняться к гиперповерхности. При удалении от оси цилиндра на определенное критическое расстояние они развернутся так, что локальная временная ось будет смотреть в противоположном направлении по сравнению с исходным. С этой дистанции начнем перемещаться в прошлое (относительно направления времени в исходной точке) и сможем вернуться в стартовую позицию и попасть в собственное прошлое. При этом локально мы все время будем перемещаться в свое будущее, никогда не покидая внутренней области светового конуса (такие четырехмерные траектории, или мировые линии, называются времениподобными). Что-то вроде прогулки по круговой аллее — неизменно двигаясь вперед, приходим на прежнее место. На языке теоретической физики это можно выразить так: во вселенной Гёделя существуют замкнутые времениподобные мировые линии.
Прошлое нашего мира
Курт Гёдель очень хотел узнать, не напоминает ли наш мир его модель. Знаменитый физик-теоретик Фримен Дайсон, который в те годы тоже работал в Институте фундаментальных исследований, вспоминал, что Гёдель не раз спрашивал его, не обнаружили ли астрономы вращение Вселенной. Совсем недавно американские физики, возглавляемые профессором Мичиганского университета Майклом Лонго, пришли к заключению, что такое возможно. Однако даже если эта гипотеза подтвердится, с путешествиями во времени все равно ничего не выйдет. Спектральный анализ реликтового микроволнового излучения неопровержимо свидетельствует о том, что если наша Вселенная и вращается, то чрезвычайно медленно (не говоря уже о том, что она расширяется с возрастающей скоростью). В общем, как однажды заметил английский писатель викторианской эпохи Сэмюэл Батлер, даже Всевышний не в силах изменить прошлое — это под силу только историкам.
Световой конус
Полезное
Смотреть что такое «Световой конус» в других словарях:
Световой конус — (двумерное пространство + время) Световой конус (изотропный конус, нулевой конус) гиперповерхность в пространстве времени (чаще всег … Википедия
СВЕТОВОЙ КОНУС — понятие используемое при описании геом. св в четырёхмерного пространства времени в частной (специальной) и общей теории относительности. С. к., соответствующим данной точке пространства времени, наз. трёхмерное подпространство в этом… … Физическая энциклопедия
световой конус — šviesos kūgis statusas T sritis fizika atitikmenys: angl. light cone; luminous cone vok. Lichtkegel, m; Lichtkonus, m rus. световой конус, m pranc. cône de lumière, m … Fizikos terminų žodynas
световой конус — (син. рефлекс световой) наблюдаемое при отоскопии отражение света от барабанной перепонки в виде блестящего треугольника, расположенного в ее передненижнем сегменте и обращенного вершиной к центру; исчезновение С. к. или изменение его формы имеет … Большой медицинский словарь
прошлый световой конус — neigiamasis šviesos kūgis statusas T sritis fizika atitikmenys: angl. minus light cone; negative luminous cone vok. negativer Lichtkonus, m rus. прошлый световой конус, m pranc. cône de lumière passée, m … Fizikos terminų žodynas
будущий световой конус — teigiamasis šviesos kūgis statusas T sritis fizika atitikmenys: angl. plus light cone; positive luminous cone vok. positiver Lichtkonus, m rus. будущий световой конус, m pranc. cône positif de lumière, m … Fizikos terminų žodynas
Конус — Прямой круговой конус. Прямой и … Википедия
рефлекс световой — см. Световой конус … Большой медицинский словарь
Светоподобный — Световой конус Световой конус, нулевой конус гиперповерхность в пространстве Минковского, ограничивающая области будущего и прошлого относительно заданного события. Содержание 1 Определение … Википедия
Светоподобный вектор — Световой конус Световой конус, нулевой конус гиперповерхность в пространстве Минковского, ограничивающая области будущего и прошлого относительно заданного события. Содержание 1 Определение … Википедия