что такое свертка данных

Что такое свертка данных

Использован релиз 3.0.60

Свертка информационной базы 1С – это обработка документов и регистров, при которой происходит формирование документов ввода остатков на определенную дату (дату свертки) и удаление документов, которые не используются, и движений по регистрам (сведений, накопления, бухгалтерии) по дату свертки включительно. Свертка информационной базы обычно выполняется, чтобы сократить объем данных в рабочей базе и увеличить скорость работы системы.

Перед сверткой обязательно создайте резервную копию базы данных (этап входит в процедуру свертки) на случай, если процедура свертки закончится неудачно и потребуется восстановить данные. Также в будущем может потребоваться сформировать отчеты по прошлым «отрезанным» периодам. В этом случае для восстановления архива (копии) создайте новую базу. Как это сделать, см. в ответе на вопрос «Как в «1С:Бухгалтерии 8″ (ред. 3.0) восстановить копию информационной базы до свертки?».

Процесс свертки информационной базы включает следующие этапы: создание резервной копии, настройку свертки, формирование документов ввода остатков, просмотр операций, проверку и удаление старых документов.

Свертку может выполнить только пользователь с правами «Администратор». Если с программой одновременно работают несколько пользователей, им необходимо завершить работу и выйти из программы.

Перед выполнением свертки информационной базы рекомендуется:

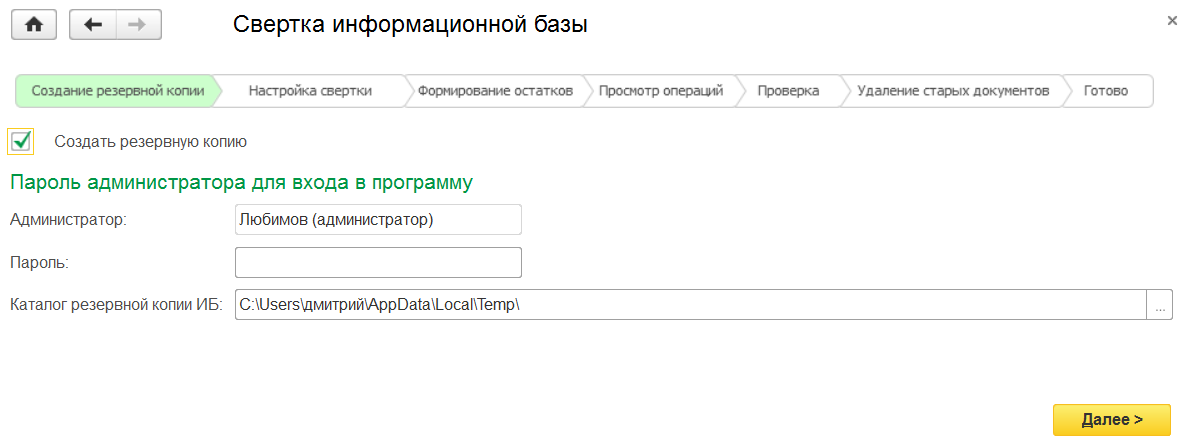
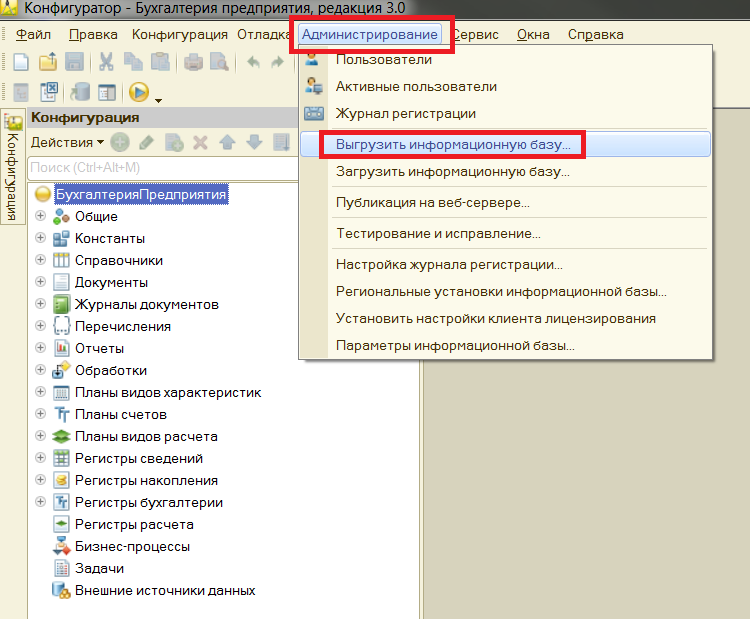
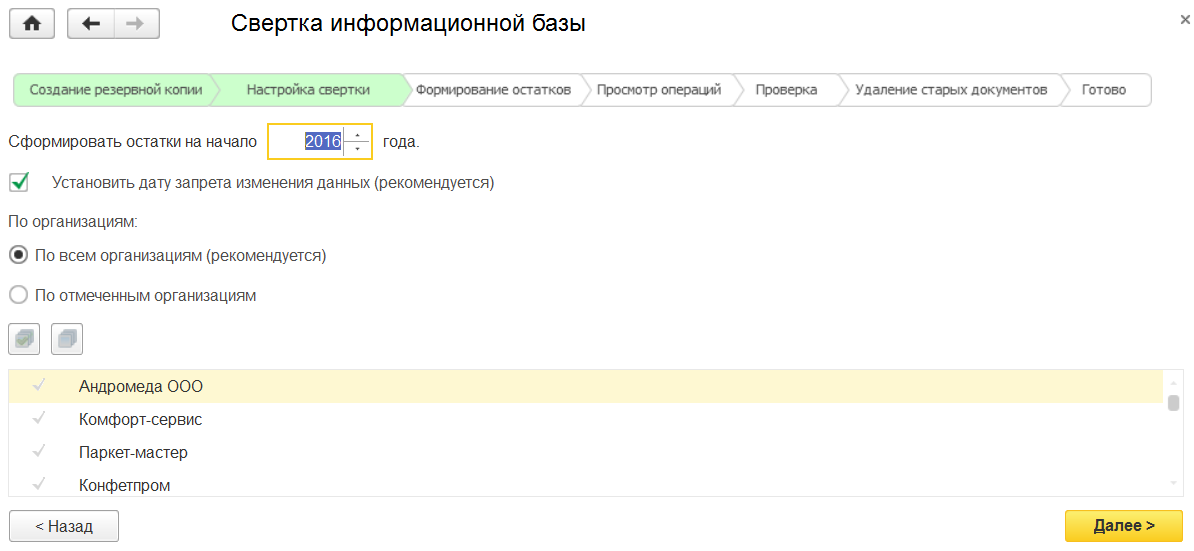
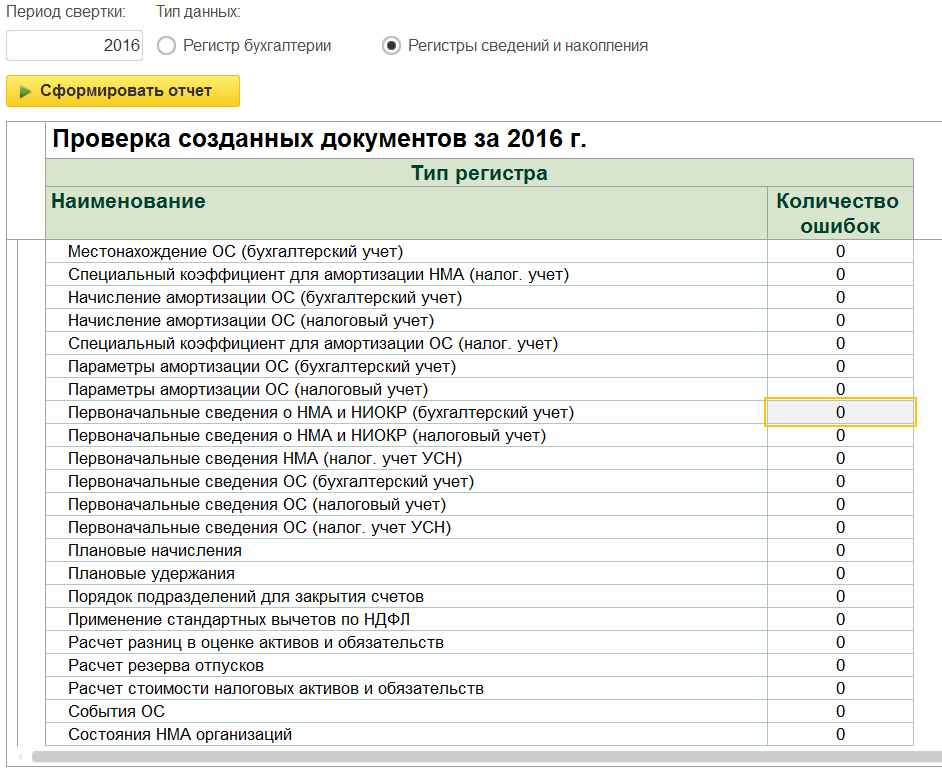
Для проведения свертки информационной базы (рис. 1):

Откройте журнал операций, все документы прошлых периодов (до свертки) в нем помечены на удаление, кроме документов по учету ОС и НДС. Чтобы проверить, у каких документов не установлены пометки на удаление, нажмите кнопку «Реестр документов», установите период, за который выполнялась свертка базы. Нажмите кнопку «Показать настройки», затем кнопку «Добавить», выберите «Пометка на удаление», вид – сравнение «равно» и значение «нет». Сформируется реестр с объектами, которые не помечены на удаление.

Для окончательного удаления из базы объектов, помеченных на удаление, отройте раздел «Администрирование» и перейдите по ссылке «Удаление помеченных объектов».

Смотрите также

Источник

Как сделать свертку базы 1С 8.3 Бухгалтерия

Зачем делать свертку базы в 1С

Для начала немного теоретических данных.

В программе 1С:Предприятие 8 можно работать в двух режимах:

Информация, предоставленная ниже, актуальна только для файлового режима.

Для начала стоит знать, что в случае файлового размещения программа имеет существенные ограничения по размерам файлов. Это значит, что размер одной таблицы не должен быть больше 4 Гб, иначе программа просто перестанет запускаться, а при приближении к указанному порогу начнет заметно «тормозить». Таким образом свертка позволит существенно уменьшить размер таблиц и повысить производительность базы данных. В первую очередь это касается регистра бухгалтерии, как наиболее «тяжелой» из всех таблиц.

В чем заключается операция свертки базы данных:

Такая операция позволит существенно уменьшить размер регистра бухгалтерии и таким образом повысить быстродействие и эффективность программы.

Как делать свертку базы в 1С

В программе в разделе Администрирование открываем раздел Обработка свертки:

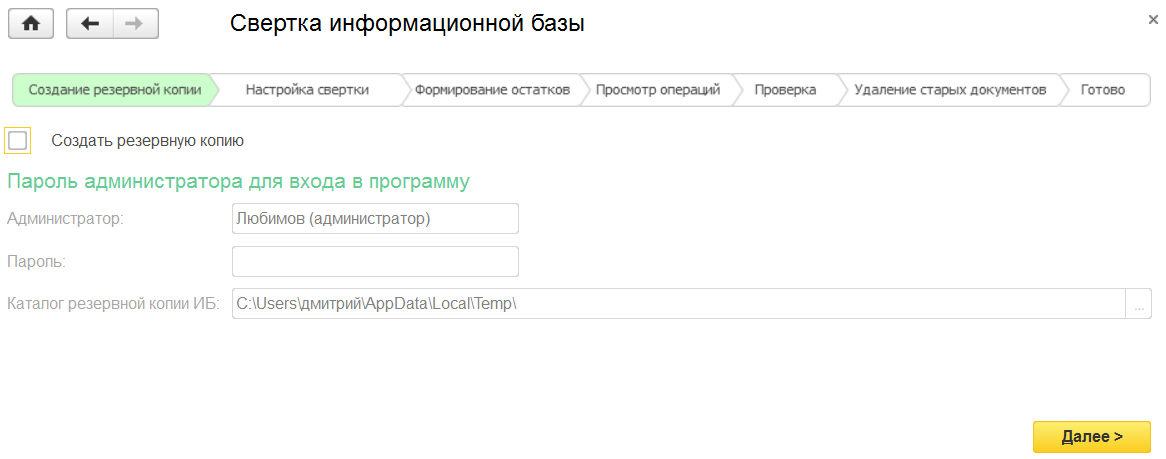
Далее нажимаем на Создать резервную копию, указывая при этом данные пользователя, под которым необходимо сделать копию, а также каталог, куда ее сохранить. Нажимаем кнопу Далее и появившемся окне подтверждаем операцию (нажимаем Да):

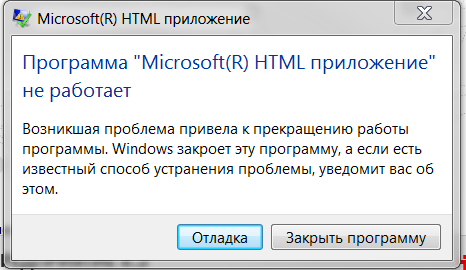
Здесь выскакивает ошибка. Не пугаемся и делаем перезапуск программы.

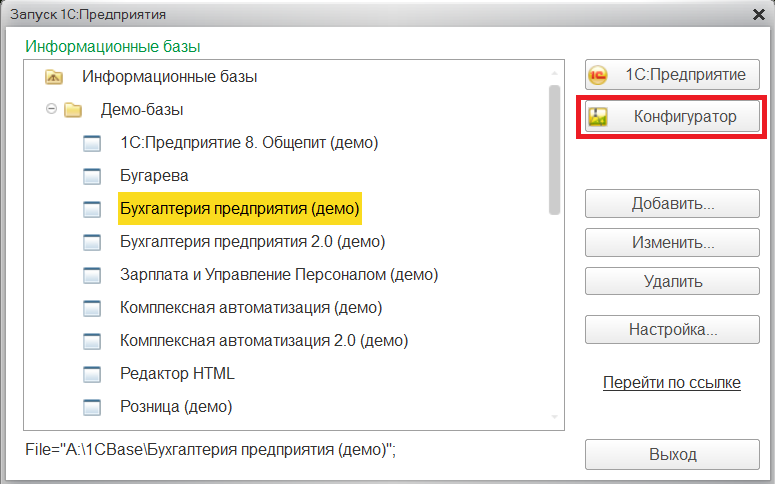
Ситуация снова повторяется, но это так и надо. Теперь делаем копию вручную и переходим в конфигуратор:

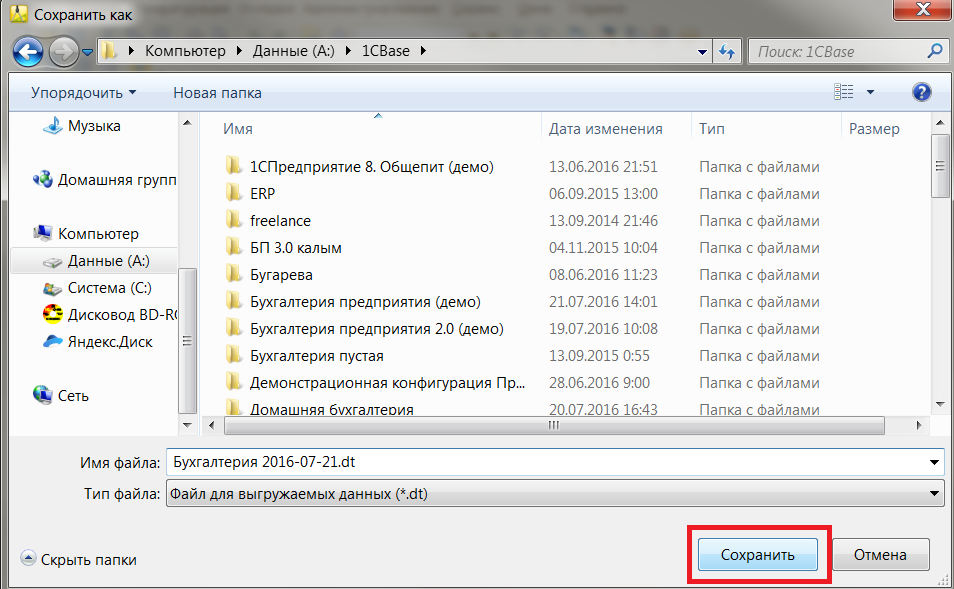
Выбираем место хранения копии и присваиваем ей имя:

Видим такое сообщение:

Снова возвращаемся в обработку свертки и снимаем признак создания копии снимаем. Нажимаем кнопку Далее:

В следующем окне выбираем год или период, на начало которого производится свертка. При этом очень желательно Установить дату запрета, ранее которой в базе уже ничего не вводилось. Что касается списка организаций, то свертку можно делать как по всему списку, так и по его отдельным пунктам:

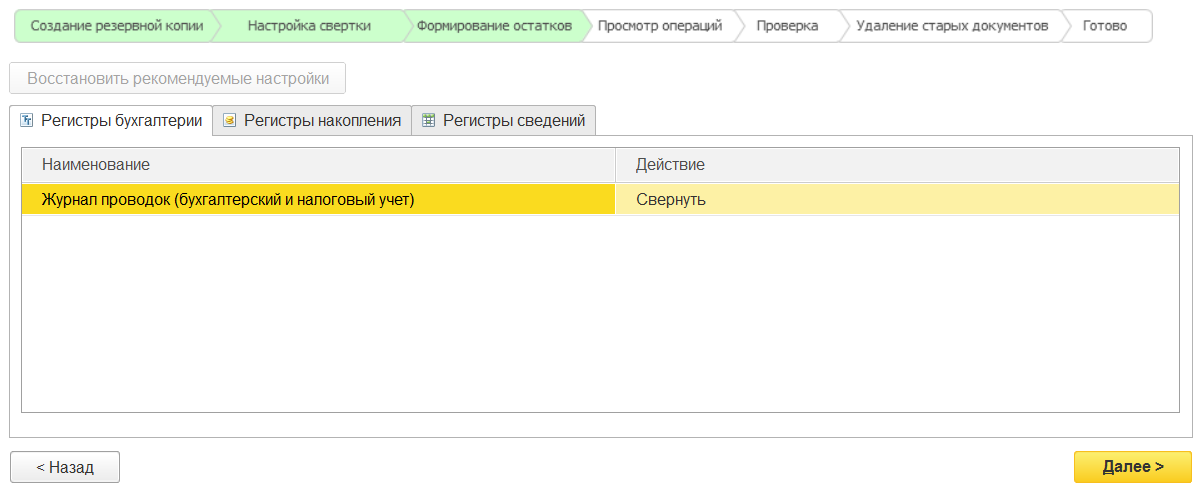
Следующее окно показывает каким образом программа планирует обработать таблицы, например, некоторые из них предлагает оставить без изменения, а некоторые — свернуть. Без изменения останутся большинство регистров сведений, а также регистры накопления по НДС, поскольку размер их не критичен. Обычно в приоритете свертка регистра бухгалтерии.

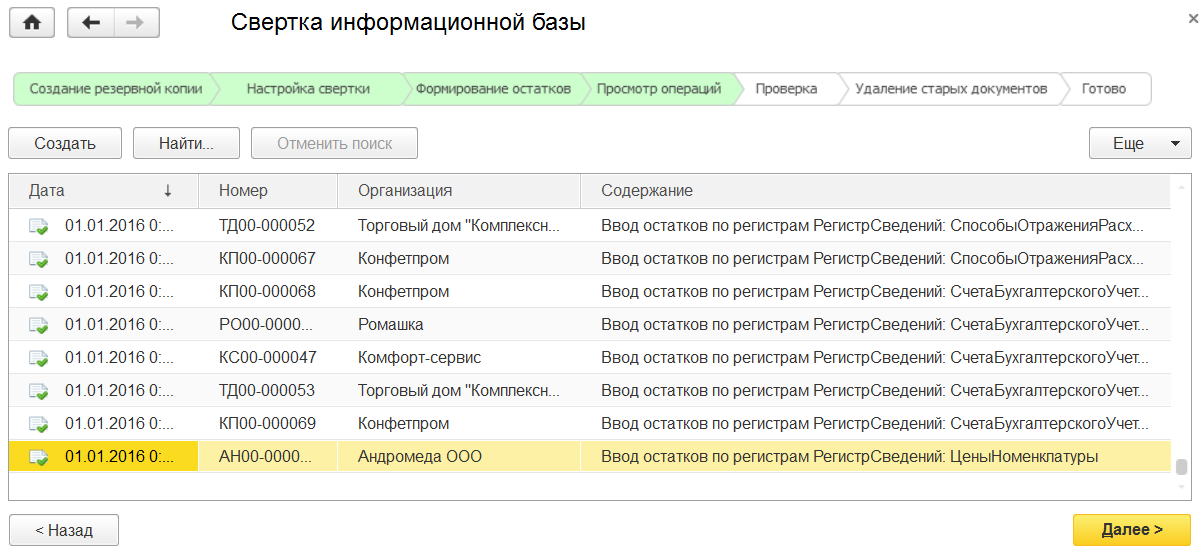
Далее программа выводит на экран список документов Операция. Эти документы будут созданы для внесения в них остатков (где они есть) по всем статьям бухгалтерского учета на начало периода.
Двигаемся дальше.

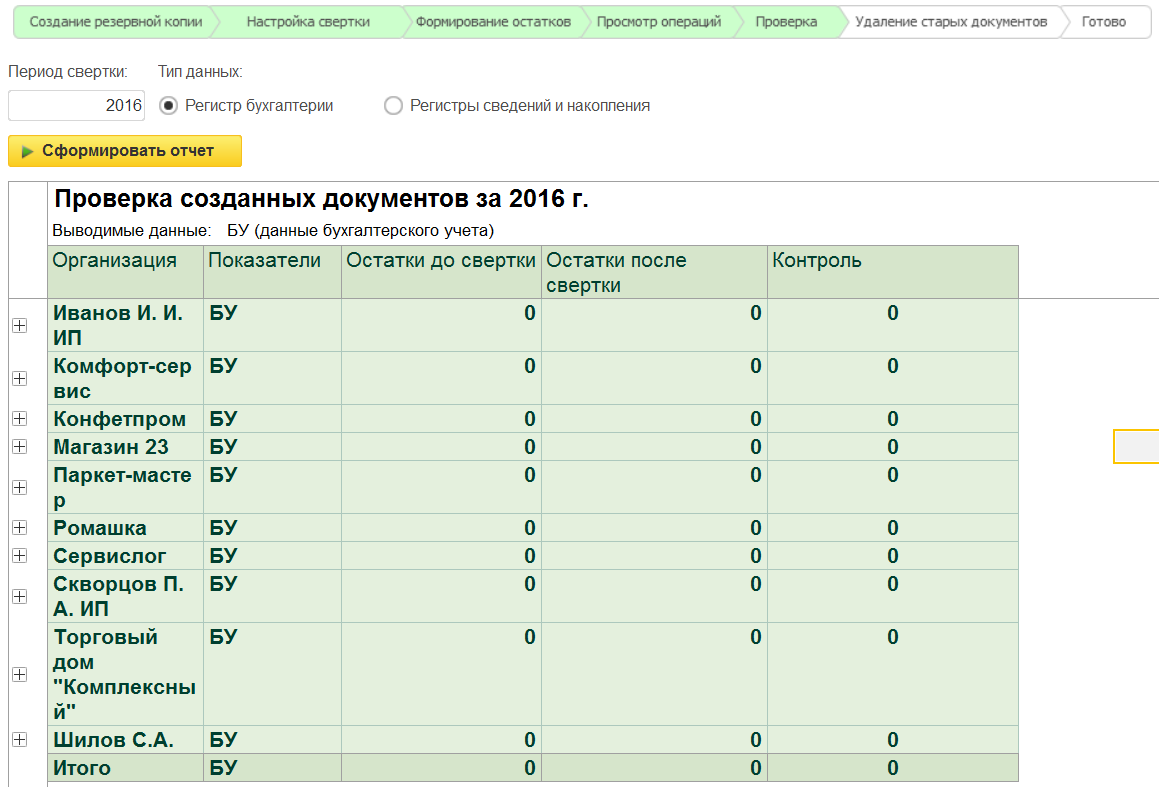
В следующем окне мы видим сводную таблицу с анализом остатков на начало периода. Их корректность проверяется сравнением с начальными остатками на момент, который предшествовал свертке. Скриншот, приведенный ниже, показывает, что все остатки являются корректными.

На всякий случай таким же образом следует проверить таблицу сверки по регистрам накопления и сведений:

Следующее окно программы предупреждает о начале процедуры удаления документов до Даты запрета (в данном случае это 2016 год). Подтверждаем операцию.

После того как документы удалены на экран выводится сообщение об успешно произведенной свертке.

Стоит обратить внимание на один важный момент: по причине того, что движение по большинству регистров накопления в части НДС и регистров сведений остались в базе, то и первичные документы, предшествующие их создание, тоже сохранились в системе. Пусть это никого не смущает, ведь нашей целью было добиться «облегчения» регистра бухгалтерии и нам это удалось.

Источник

Руководство для начинающих по сверточным нейронным сетям (CNNs)

Дата публикации Feb 15, 2019

Что такое свертка?

Например, есть изображение Эйлин Коллинз, а матрица над красной стрелкой используется в качестве свертки для обнаружения темных краев. В результате мы видим изображение, на котором выделены только темные края.

Обратите внимание, что изображение является двухмерным с шириной и высотой. Если изображение цветное, считается, что оно имеет еще одно измерение для цвета RGB. По этой причине 2D-свертки обычно используются для черно-белых изображений, а 3D-свертки используются для цветных изображений.

Свертка в 2D

Давайте начнем с (4 x 4) входного изображения без заполнения, и мы используем (3 x 3) сверточный фильтр для получения выходного изображения.

Первым шагом является умножение желтой области на входном изображении с помощью фильтра. Каждый элемент умножается на элемент в соответствующем месте. Затем вы суммируете все результаты, которые являются одним выходным значением.

Математически это (2 * 1) + (0 * 0) + (1 * 1) + (0 * 0) + (1 * 0) + (0 * 0) + (0 * 0) + (0 * 1) + (1 * 0) = 3

Затем вы повторяете тот же шаг, перемещая фильтр на один столбец. И вы получите второй выход.

Обратите внимание, что вы переместили фильтр только на один столбец. Размер шага, когда фильтр скользит по изображению, называетсяшаг, Здесь шаг равен 1. Эта же операция повторяется, чтобы получить третий вывод. Размер шага больше 1 всегда уменьшает размер изображения. Если размер равен 1, размер изображения останется прежним.

Наконец, вы получаете окончательный результат.

Мы видим, что размер выходного изображения меньше размера входного изображения. На самом деле это верно в большинстве случаев.

Свертка в 3D

Свертка в 3D такая же, как и в 2D, за исключением того, что вы выполняете двумерную работу 3 раза, потому что есть 3 цветовых канала.

Обычно ширина вывода уменьшается, как и размер вывода в 2D-случае.

Если вы хотите, чтобы выходное изображение было одинаковым по ширине и высоте без уменьшения размера фильтра, вы можете добавить отступы к исходному изображению с нулями и сделать сверточный срез изображения.

Мы можем применить больше отступов!

Как только вы закончите, вот как будет выглядеть результат:

Когда вы добавляете больше фильтров, это увеличивает глубину выходного изображения. Если у вас есть глубина 4 для выходного изображения, 4 фильтра были использованы. Каждый слой соответствует одному фильтру и запоминает один набор весов. Это не изменяется между шагами, поскольку это скользит через изображение.

Выходной канал сверток называетсякарта объектов, Он кодирует наличие или отсутствие и степень присутствия обнаруживаемой функции. Обратите внимание, что, в отличие от 2D-фильтров, каждый фильтр подключается ккаждыйвходной канал. (вопрос? что означает, что каждый фильтр подключается к каждому входному каналу в отличие от 2D?) Это означает, что они могут вычислять сложные функции. Первоначально, глядя на каналы R, G, B, а затем, глядя на комбинации изученных особенностей, таких как различные ребра, формы, текстуры и семантические особенности.

Перевод-инвариантная

Другим интересным фактом является то, что CNN несколько устойчивы к трансляции, такой как немного сдвигаемое изображение, которое будет иметь карту активации, аналогичную той, которая была перед сдвигом. Это связано с тем, что свертка является детектором признаков, и если она обнаруживает темный край и изображение перемещается вниз, темные края не будут обнаруживаться, пока свертка не будет перемещена вниз.

Здесь рассматривается 1D свертка, потому что она обычно недостаточно объяснена, но имеет значительные преимущества.

Они используются для уменьшения глубины (количества каналов). Ширина и высота в этом случае не изменяются. Если вы хотите уменьшить горизонтальные размеры, вы должны использовать объединение, увеличить шаг свертки или не добавлять отступы. 1D свертки вычисляет взвешенную сумму входных каналов или функций, которые позволяютвыбор определенных комбинаций функций, которые полезны 1D свертка сжимается, потому что есть только один, он имеет тот же эффект

объединение

Max-Pooling

Максимальный пул используется для уменьшения размера изображения путем сопоставления размера данного окна в единый результат, принимая максимальное значение элементов в окне.

Средний-Pooling

Это то же самое, что и max-pooling, за исключением того, что оно усредняет окна, а не выбирает максимальное значение.

Общая настройка

Для реализации CNN наиболее успешная архитектура использует один или несколько стеков уровней свертки + пул с повторной активацией, за которыми следует плоский слой, а затем один или два плотных слоя.

По мере продвижения по сети карты пространственных объектов уменьшаются в пространстве и увеличиваются по глубине. Особенности становятся все более абстрактными и теряют пространственную информацию. Например, сеть понимает, что изображение содержало глаз, но не знает, где оно было.

Вот пример типичной сети CNN в Керасе.

Вот результат, когда вы делаете model.summary ()

Давайте разберем эти слои и посмотрим, как мы получим эти номера параметров.

Conv2d_1

Размер фильтра (3 x 3) * глубина ввода (1) * количество фильтров (32) + смещение 1 / фильтр (32) = 320. Здесь глубина ввода равна 1, поскольку она используется для черно-белых данных MNIST. Обратите внимание, что по умолчанию в тензорном потоке к каждому слою свертки добавлено смещение.

Max_pooling2d_1

Слои пула не имеют параметров

Conv2d_2

Размер фильтра (3 x 3) * глубина ввода (32) * количество фильтров (64) + смещение, 1 на фильтр (64) = 18496

Flatten_1

Размещает том над ним в массив.

Dense_1

Входной размер (128) * Выходной размер (10) + Одно смещение на выходной нейрон (10) = 1290

Резюме

источники

Этот учебник основан на лекциях из курса прикладного глубокого обучения в Колумбийском университетеДжошуа Гордон, Потрясающие 3d изображения изМартин Горнер,

Источник

3D ML. Часть 5: Свертки на графах

В предыдущих заметках данной серии мы уже успели поговорить о датасетах и инструментах, функциях потерь и примерах прикладных задач, а сейчас пора перейти к “ядру” любой подобласти глубокого обучения — к их архитектурам. Но, прежде чем разбираться с тем как устроены целые архитектуры, стоит разобраться в их составных частях, делающих их пригодными для применения к неевклидовым данным.

Наверное вы уже догадались, что речь сегодня пойдет о сверточных операторах на графах.

Серия 3D ML на Хабре:

Репозиторий на GitHub для данной серии заметок.

Заметка от партнера IT-центра МАИ и организатора магистерской программы “VR/AR & AI” — компании PHYGITALISM.

Откуда брать информацию и на чем практиковаться?

Про графы, свертки и машинное обучение по отдельности сказано и написано многое. Если рассматривать эти три темы в одной, то список источников сокращается, однако, у неподготовленного исследователя, который решил разобраться в данном вопросе, скорее всего, не возникнет четкого понимания куда смотреть и с чего начать.

Здесь стоит отметить, что свертки на графах можно рассматривать как в общем виде, не привязываясь к конкретной предметной области, так и учитывать особенности данных с которыми вы работаете.

С наиболее общего ракурса, тема сверток на графах хорошо освещена в обзорной статье “Representation Learning on Graphs: Methods and Applications” [1]. Методам машинного обучения на графах посвящены целые университетские спецкурсы, наиболее известным из которых является Stanford CS224W: Machine Learning with Graphs. По мотивам этого курса есть разбор от русскоязычного сообщества исследователей Sberloga, в котором есть записи обсуждения лекций, примеры кода, разбор разных аспектов теории и практики и многое другое. Также стоит отметить вот эту статью с хабра от ODS, в которой упоминается о схожем сообществе для разбора стенфордского курса и заодно изложены несколько основных подходов к получению скрытых представлений графов (т.н. эмбеддинги).

В более сжатом виде есть несколько серий заметок на эту тему на Medium:

Для области 3D ML методы и алгоритмы, основанные на извлечении информации из графовых структур, являются важным подспорьем. Объекты интереса — это зачастую полигональный меш, который сам по себе является пространственным графом (см. например работу [15]), или облако точек, которое также можно мыслить как графовую структуру, если соединять между собою точки в облаке по определенным правилам (см. например работу [14]). Про различные виды сверток на графах, применительно к задачам 3D ML, можно прочитать в нашем обзоре про алгоритмы семантической сегментации облака точек.

С точки зрения инструментов, в основном исследователи в данной области пользуются либо собственноручно написанными библиотеками, либо библиотеками, которые первоначально предназначались для работы с графами в предметной области (например библиотека python rdkit или python NetworkX). На наш взгляд, наиболее удобной библиотекой для построения собственных глубоких архитектур на основе графовых сверток является PyTorch Geometric (на странице с документацией можно найти различные примеры графовых датасетов, методов их обработки и загрузки, и различных сверточных слоев). В репозитории библиотеки TensorFlow Graphics также можно найти пример “Semantic mesh segmentation”, в котором, с помощью встроенных в библиотеку сверточных операторов, конструируют небольшую глубокую архитектуру для решения задачи семантической сегментации меша. Рекомендуем всем начинающим 3D ML исследователям самостоятельно разобрать описанные выше примеры.

Ниже, в основном повторяя данный туториал Бориса Князева из пункта 4, мы постараемся разобраться в том как устроены свертки на графах на базовом уровне, чем они отличаются от сверток на изображениях.

Граф как неевклидова структура

Рис.1 Пример из статьи [2]: левые изображения демонстрируют, что стандартная свертка (Euclidean CNN) будет по разному обрабатывать данные в зависимости от типа поверхности к которой ее применяют, что, в свою очередь, мотивирует к созданию геометрических сверток (Geometric CNN, правые изображения).

Свертка — замечательный инструмент, позволяющий “аккумулировать” информацию о близлежащих (локальных) частях в данных. В случае с изображениями, мы естественным образом предполагаем, что соседние пиксели скорее всего связаны семантически (являются частью одного объекта). Поскольку одна и та же свертка применяется ко всем пикселям изображения, оператор, основанный на ней, становится независим к размеру изображения и занимает меньше памяти. Исходя из этого соображения, становится несложно понять, почему сверточные сети стали так популярны для обработки изображений.

Более формально, общие свойства евклидовых и неевклидовых данных были описаны в обзорной статье “Geometric deep learning: going beyond Euclidean data” [2] (всем познающим 3D ML, на наш взгляд, обязательно к ознакомлению).

Кратко перечислим свойства евклидовых данных:

Для графов эти свойства обычно не выполняются. Наша задача — научиться конструировать такой же удобный как классические свертки инструмент для неевклидовых структур данных (в нашем случае для графов).

Для того, чтобы лучше понять идею стоящую за такой конструкцией, попытаемся взглянуть на изображения (евклидова структура) как на графы (неевклидова структура).

Рис.2 Слева: изображение из датасета MNIST; справа: граф построенный по пикселям данного изображения. (см. работу [3]).

Структуру изображения, являющуюся многомерным массивом, у которого для каждого пикселя определены два соседа вдоль каждого измерения, можно представить в виде регулярной узловой решетки, как на изображении ниже. Для подобных визуализаций используется библиотека python NetworkX. На хабре есть хорошая вводная статья в этот фреймворк.

Как создать граф на изображении ниже:

Теперь попробуем применить стандартные свертки для таких регулярных сетей и попытаемся понять, почему такой подход сложно обобщить на графы произвольной структуры.

В качестве примера можно рассмотреть свертку, определяемую матрицей . Пусть в узлах нашей решетки хранятся некоторые числовые значения, например, интенсивность цвета пикселя записанные в матрицу — . Применение свертки обычно выражено в виде скалярного произведения (dot product) матрицы фильтра на матрицу значений в узлах сетки (это может быть подграф всей сети), совпадающую по размерам с фильтром (см. рисунок ниже). Хороший и подробный туториал по применению сверток к изображениям содержится в статье “A guide to convolution arithmetic for deep learning” [4].

Обратим внимание, что каждому узлу фильтра всегда найдется узел в данных, к какой бы точке данных мы не прикладывали этот фильтр. Для графов общего вида это утверждение не верно, что, соответственно, создает нам проблемы, если мы попытаемся применить данный фильтр к ним.

Операторы, вроде скалярного произведения, рассмотренного выше, относят к классу агрегирующих функций — методов сохранения информации о многих объектах в одном (в данном случае, результатом свертки является одно число, полученное из 9 исходных). Другим способом агрегировать информацию является использование т.н. pooling операций в сверточных сетях. Здесь важно заметить, что такие операции инвариантны к перестановке пикселей, в отличие от скалярного произведения рассмотренного выше, поскольку в общем случае

Кстати, рассмотрение изображений как регулярных графовых сетей приводит к интересному результату. Мы можем рассматривать иное разбиение изображения на составные части нежели исходные пиксели, например каким-либо способом объединять группы пикселей в т.н. “суперпиксели” и строить свертки нерегулярной структуры над ними. Про такой подход к обработке изображений можно прочитать в данной заметке.

Рис.3 Пример построение суперпикселей разного разрешения на изображении из работы [5].

Теперь попробуем обобщить свертки на нерегулярные графы. Здесь мы столкнемся со следующей проблемой: граф в общем виде — совокупность двух множеств (вершины — , и связи между этими вершинами — ), а множества — инвариантный к перестановке элементов тип данных. Это значит, что мы можем случайным образом перемешать вершины графа (с учетом соответствующего перемешивания связей) и при этом сам граф останется прежним, но как было отмечено выше — свертка зависит от порядка элементов.

Поскольку не существует какой-то канонической расстановки вершин произвольного графа, требуется определить операцию свертки так, чтобы она не зависела от этой расстановки. Наиболее популярные способы определить свертку на графе — использование операторов на основе усреднения (averaging) [6] или суммирования (summation) [7] по всем соседям рассматриваемой вершины, с последующим умножением на матрицу весов . Таким образом, мы агрегируем всех соседей вместе с самой вершиной и проецируем граф через свертку в пространство другой размерности. Про различные виды агрегирующих операторов на графах можно прочитать в статье [8].

Рассмотрим для лучшего понимания граф состоящий из 5 вершин на изображении ниже (рис.4). Применяя агрегирующий оператор на основе суммирования для вершины получим новое значение признака этой вершины:

Таким образом, после применения оператора агрегирования, исходный граф сохраняет свою структуру, но в вершинах хранятся признаки с агрегированной информацией о соседях и теперь можно использовать матрицу признаков в вершинах графа для дальнейшей работы вне зависимости от того, как вершины исходно были пронумерованы.

Рис.4 Пример нерегулярных графов и схематичное изображение соседей рассматриваемых вершин .

Поскольку рассмотренные выше агрегирующие операторы применяются ко всем вершинам графа и позволяют собрать информацию о соседях в одном месте их называют “свертками” на графе. Однако, сконструированные таким образом свертки никак не учитывают топологию графа. Попробуем разобраться, как можно улучшить эти операторы с учетом топологического фактора.

Конструируем сверточный слой для графов

Сначала вспомним, как конструируется полносвязный слой в классической полносвязной архитектуре (В качестве примера будем держать в голове классификацию рукописных цифр из MNIST). Пусть — вектор значений на -ом слое, — матрица весов -го слоя. Тогда линейный полносвязный линейный слой может быть записан в виде:

После матричного умножения, в глубоком обучении принято налагать нелинейность (активационная функция нейрона), однако, если мы говорим о MNIST данных, оказывается можно обойтись только линейной частью и добиться доли правильных ответов на тестовой выборке в 91% (здесь есть пример реализации такой сети).

Теперь давайте попробуем ввести в эту формулу множитель, который описывал бы топологию данных (в нашем случаи — графа). Для этого мы будем использовать матрицу смежности — . Ниже приведен пример неориентированного графа и его матрицы смежности. Обратите внимание, что различные варианты нумерации вершин графа приводят к различным матрицам смежности.

Рис.5 Неориентированный граф из 5 вершин и его матрица смежности (голубой цвет — 0, желтый — 1) для двух вариантов нумерации вершин графа.

Давайте определим матрицу смежности для регулярной сети, соответствующей растровому изображению размера в примере с MNIST. Для этого этого воспользуемся стандартными приемами из numpy:

В данном случае, матрица dist — матрица смежности для полносвязного графа с вершинами, матрица — матрица смежности с учетом пространственной близости (здесь используется эвристическое соображение о том, что близлежащие пиксели должны сильнее коррелировать друг с другом чем те, что лежат на расстоянии). Этот способ определять матрицы смежности для задач, связанных с обработкой изображений, — популярный, но далеко не единственный (см. альтернативы в работах [2, 9]).

Рис.6 Слева-направо: матрица смежности в форме расстояний между пикселями, матрица смежности в форме пространственной близости, подграф полносвязного графа рассматриваемого изображения .

Теперь, на основе матрицы смежности , мы сможем сконструировать т.н. нормированную матрицу смежности . Ее можно сконструировать разными способами, но два наиболее популярных подхода следующие:

В итоге, после выбора способа нормализации матрицы смежности, мы сможем сконструировать линейный полносвязный слой вида:

Если к результату матричного умножения в правой части применить нелинейную функции активации, то мы сконструируем нелинейный полносвязный слой.

Можно написать достаточно простой код на основе операторов PyTorch, чтобы увидеть разницу в реализации обычного полносвязного слоя и полносвязного слоя с графовой сверткой:

Полный код для данного примера можно найти в оригинальном репозитории здесь. Кстати, если вы попытаетесь сравнить качество обучения на MNIST для обычной и для графовой модели, вы обнаружите, что качество отличается несущественно. Это происходит по той причине, что для данного конкретного датасета, связи между пикселями в рукописных цифрах и так очень сильны, но что более важно, оператор здесь есть не что иное, как Гауссовский фильтр, поэтому такая архитектура графовой сети приводит фактически к тому, что у нас есть обычная сверточная нейронная сеть с фиксированным Гауссовским фильтром. Чтобы сверточная архитектура на регулярных графах работала лучше, можно применить ряд трюков, которые описаны в работах [10, 11, 12].

Рис.7 Гауссовский фильтр, использовавшийся в нейронной сети, описанной выше (слева) и результат его применения к изображению (справа).

В качестве примера подобного трюка, можно рассмотреть слой, который позволяет детектировать границу разделения между любой парой пикселей:

Рис.8 2D-фильтр нейронной сети, описанной выше, с центром в красной точке. Усреднение (слева, точность 92,24%), обучение на основе координат (посередине, точность 91,05%), обучение на основе координат с некоторыми трюками (справа, точность 92,39%).

Можно заметить, что фильтр, который мы только что обучили (в середине), выглядит странно. Это связано с тем, что задача довольно сложная, поскольку мы оптимизируем две модели одновременно: модель, которая предсказывает разделяющую поверхность для групп пикселей, и модель, предсказывающая класс цифры. Чтобы узнать лучшие фильтры (например, тот, что справа), нам нужно применить некоторые другие приемы, которые можно найти в работе [13].

Выводы

Графовые нейронные сети (GNN) — это очень гибкое и интересное семейство нейронных сетей, которые могут быть применены к действительно сложным данным. Как всегда, такая гибкость должна иметь определенную цену. В случае GNN — это трудность регуляризации модели путем определения таких операторов как свертка. Исследования в этом направлении продвигаются довольно быстро, так что GNN найдут применение во все более широких областях машинного обучения и компьютерного зрения.

Рис.9 Граф работ по конструированию GNN архитектур из туториала Бориса Князева “Anisotropic, Dynamic, Spectral and Multiscale Filters Defined on Graphs”.

Более детальный обзор подходов к конструированию сверток на графах, вы сможете найти в оригинальном туториале от Бориса Князева и его продолжениях.

Тем из вас, кому стало интересно как же расшифровывается формула с обложки, рекомендуем к ознакомлению статью [6].

Для всех кому интересно углубиться в тему сверток на графах, рекомендуем прочитать оставшиеся два туториала в серии заметок Бориса Князева на Medium.

Источник