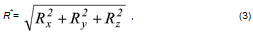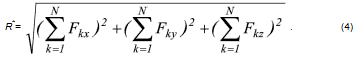что такое система сходящихся сил и равнодействующая сходящихся сил
Теоретическая механика
4. Система сходящихся сил
Условие равновесия сходящейся системы сил
Пусть на тело действует сходящаяся система сил 
(рис. С14).
На основании следствия из аксиомы №2 перенесем все силы в точку пересечения линий действия сил О.
Уравнение (С.1) является уравнением равновесия сходящейся системы сил в векторной форме.
Запишем условие равновесия в координатной форме. Для этого разложим все действующие силы по осям координат
Тогда в соответствие с уравнением (С.1) можно записать
Из формулы (С.4) следует, что вектор 
равен нулю, значит и проекции вектора на оси координат тоже равны нулю
Система уравнений (С.5) является координатной формой записи условия равновесия сходящейся системы сил.
Груз в виде шара подвешен на нити, как указано на рис.С.16.
iSopromat.ru
Равнодействующая системы сходящихся сил приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.
Система сходящихся сил
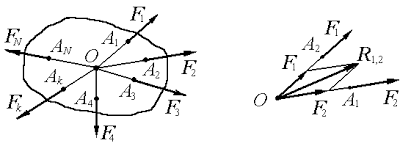
Пусть, к абсолютно твердому телу приложена система N сил (F1, F2, … FN), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).
Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.
Приведение к равнодействующей
Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.
В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О.
Далее, по четвертой аксиоме, силы F1 и F2 можно заменить их равнодействующей R1,2 (рисунок 1), которая определяется диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.
Далее можно записать аналогичные соотношения для полученной равнодействующей силы R * 1,2 и силы F3, тогда
Для системы N сил окончательно будем иметь
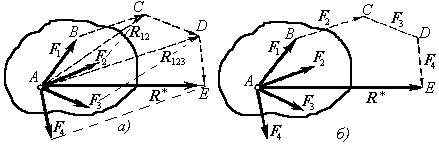
На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника.
Силовой многоугольник
Из конца вектора силы F1 (точки В) проводим вектор ВС, геометрически равный силе F2. Из конца этого вектора (точки С) проводим вектор СD равный силе F3. Из конца этого вектора (точки D) проводим вектор DE, равный силе F4.
Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами.
Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника.
Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах.
Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.
Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.
Вычисление равнодействующей
Для аналитического определения равнодействующей найдем ее проекции Rx, Ry, Rz на оси декартовой системы координат. Имеем
Тогда величина равнодействующей определится следующей формулой:
Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:
Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.
В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Плоская система сходящихся сил
Содержание:
Плоская система сходящихся сил – это система сил линии действия которых сходятся в одной точке, называются сходящимися.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Если все силы, приложенные к телу, расположенные в одной плоскости и линии их действия пересекаются в одной точке, то такая система сил носит название плоской системы сходящихся сил.
Покажем на рис. 1.6 произвольное тело, к которому приложена плоская системы сходящихся сил 
, 
, 
. 
. При этом линии действия всех сил пересекаются в точке A.
Определение равнодействующей системы сходящихся сил
Геометрический способ сложения сил:
Добавить систему сил означает определить их равнодействующую. Попробуем найти равнодействующую для плоской системы сходящихся сил, которая изображена на
рис. 1.6. Возьмем (условно) две первые силы и и на основании III аксиомы
статики найдем их равнодействующую 
, для чего на силах и , как на
сторонах, построим свой параллелограмм, диагональ которого, которая приложена в
точке A, и является их равнодействующей . Далее геометрически добавим две следующие силы и , и уже на этих силах как на сторонах построим свой
параллелограмм, диагональ которого будет второй равнодействующей 
. Так же дальше продолжаем до последней силы 
. Когда построено последний параллелограмм и проведена последняя диагональ, то она и будет равнодействующей 
системы сходящихся сил, которая показана на рис. 1.6
Если внимательно присмотреться к геометрическому построению параллелограммов, то можно увидеть, что к концу вектора силы 
был присоединен вектор силы 
(то есть в конец вектора перенесено параллельно вектор ) и так далее до последней силы .
Таким образом, геометрический способ добавления сходящихся сил сводится к построению силового многоугольника. Он строится путем параллельного переноса векторов сил в масштабе, когда начало следующей силы совпадает с концом предыдущей силы. Тогда вектор равнодействующей соединяет начало первой силы с концом последней силы. Это можно записать так:
Величина равнодействующей силы не изменится, если будет изменен порядок
присоединения (добавление) сил до многоугольника, но конфигурация силового
многоугольника будет другой.
Условие равновесия плоской системы сходящихся сил в геометрической форме
Если к свободному материальному телу приложена одна сила, то о равновесии этого тела речи не может быть. Таким образом, если рассматривать плоскую систему сходящихся сил, которая сведена к равнодействующей, то тело не может быть в равновесии.
Для равновесия тела под действием плоской системы сходящихся сил необходимо и
достаточно, чтобы равнодействующая всех сил была равна нулю.
Равнодействующая такой системы сил будет равна нулю, когда силовой многоугольник будет замкнутым, то есть когда начало вектора первой силы будет совпадать с концом вектора последней силы.
Теорема о равновесии тела под действием трех не параллельных сил
Если тело под действием системы трех плоских не параллельных сил находится в равновесии, то линии действия этих сил пересекаются в одной точке.
Представим тело (рис. 1.7), к которому в точках А, B, C приложены силы
, , , векторы которых расположены в одной плоскости. Рассмотрим сначала две силы и . На основании следствия из I и II аксиом статики указанные силы всегда можно перенести по линии их действия в одну точку, например, в точку О.
Далее, если есть в точке О две приложенные силы, то на основании III аксиомы статики их можно заменить одной силой, то есть равнодействующей 
. Построим на рис. 1.7 на указанных векторах сил и параллелограмм и покажем равнодействующую .Теперь тело находится под действием только двух сил и и оно будет в равновесии только тогда, когда векторы этих сил расположены на одной прямой, то есть на прямой CO. Тогда и вектор силы пересекает точку О. Теорема доказана.
Проекция силы на ось и на плоскость
Представим силу 
, вектор который произвольно расположен в плоскости чертежа (рис. 1.8). Выберем в этой плоскости ось, например, ось x. Необходимо спроектировать указанную силу на эту ось x.
Обозначим сначала конце вектора силы буквами А и В и опустим из них на ось x перпендикуляры. Точки пересечения перпендикуляров с осью x (обозначим их соответствующими строчными буквами а и в) образовали на оси x направленный отрезок, который и будет проекцией силы на ось x. По величине этот отрезок равен произведению модуля силы || на косинус угла, под которым вектор силы пересекает ось. А именно:
По знаку проекция силы на ось тогда будет положительная, когда угол α (угол пересечения направления вектора силы или линии действия силы с осью) острый. В полной мере разумеется, если этот угол равен в 90º, то проекция силы на ось x равна нулю. Если угол α будет тупой, то проекция силы на ось x будет иметь отрицательный знак. Значения проекции в данном случае будет
Но практически тут удобнее использовать тупой угол α2, а острый угол β между вектором силы и направлением оси x. Знак проекции легко определяется из схемы
Таким образом, проекция силы на ось — это направленный отрезок на оси, образованный между перпендикулярами, которые опущены из концов вектора силы на ось, и который по величине равен произведению модуля силы на косинус угла между направлением вектора силы и осью.
Спроектируем теперь вектор силы на плоскость и оси координат.
Возьмем силу 
, вектор которой произвольно расположен в пространстве (рис. 1.9). Выберем в пространстве прямоугольную декартову систему координат Oxyz, начало отсчета которой (точка O) совмещенное с точкой приложения вектора силы . Спроектируем вектор силы на плоскость xOy. Опустим из точки А (конец вектора силы) на указанную плоскость перпендикуляр, который пересекает ее в точке а. На плоскости xOy создан вектор 
, который и является проекцией 
силы на плоскость. По модулю эта проекция равна
где α — угол между вектором силы и плоскостью xOy.
Следует заметить, что проекция вектора силы на плоскость является вектором, потому что плоскость на имеет базисных векторов, ортов.
Если в плоскости xOy обозначить угол β, то есть возможность спроектировать силу на оси x и y, опуская с точки a на оси перпендикуляры и по известному уже правилу получить проекции вектора 
на указанные оси:
В данном случае через ось z и вектор силы можно провести плоскость, поэтому есть возможность спроектировать силу на эту ось по известному правилу. Эта проекция будет равняться
где ϒ — угол между вектором силы и осью z.
Определение силы за ее проекциями
Предположим, что у нас в плоскости рисунка имеем прямоугольную декартову систему координат Oxy, заданные две проекции силы — 
и 
(рис. 1.10). Надо по данным проекциями вычислить модуль вектора самой силы 
, а также его направление.
На заданных проекциях, как на сторонах, строим прямоугольник, диагональ которого, проходит через точку пересечения проекций, и является искомым вектором силы . Модуль силы можно определить из следующего выражения:
Углы между вектором силы и осями x и y можно определить с помощью направляющих косинусов
Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.
Аналогично для пространственной системы сил (рис. 1.9) можно построить на проекциях сила как на сторонах параллелепипед, а модуль силы определить так:
Направление вектора этой силы также определяется через направляющие косинусы его углов с соответствующими осями координат x, y и z:
Через арккосинус определяют сами углы.
Теорема о проекции равнодействующей силы на ось
Проекция вектора равнодействующей силы на ось равна алгебраической сумме проекций векторов составляющих сил на ту же ось.
Доказательство. Имеем систему сил , , , 
,которая сведена к равнодействующей 
с помощью силового многоугольника (рис. 1.11). Введем на плоскости прямоугольную декартову систему координат Ox y и спроектируем на ось x все силы. Для этого обозначим концы векторов всех сил буквами — А, В, С, D, K и проведем перпендикуляры из каждой точки на ось x. Точки пересечения перпендикуляров с осью, которые обозначены соответствующими строчными буквами — а, в, с, d, k образовали на оси x направлены отрезки, которые и являются проекциями всех сил на эту ось. Каждая проекция, соответственно, равна
Добавим алгебраически все проекции и подсчитаем, почему эта сумма равна:
Но отрезок ak и является проекцией равнодействующей силы на ось x. Распространяя эту сумму на n сил, можно записать:
Аналитический способ добавления системы сходящихся сил
На основании теоремы о проекции равнодействующей силы на ось, имеем:
Аналогично проекция равнодействующей силы на ось y будет равняться
Модуль равнодействующей равен
Углы между вектором равнодействующей и осями координат x и y определим через направляющие косинусы углов между соответствующей осью и равнодействующей:
Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.
Условия равновесия тела под действием плоской системы сходящихся сил в аналитической форме
Плоскую систему сходящихся сил можно заменить одной силой, которая носит название равнодействующей.
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы равнодействующая была равна нулю. А если равнодействующая равна нулю, то и ее проекции на оси x и y тоже должны равняться нулю. Поскольку проекции
равнодействующей равны алгебраическим суммам проекций составляющих сил, то,
окончательно, иметь условия равновесия тела под действием плоской системы
сходящихся сил
Для равновесия тела, находящегося под действием плоской системы сходящихся
сил, необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси
координат были равны нулю.
Услуги по теоретической механике:
Учебные лекции:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.