что такое псевдослучайная последовательность
Псевдослучайная последовательность
Псевдослуча́йная после́довательность (ПСП) — последовательность чисел, которая была вычислена по некоторому определённому арифметическому правилу, но имеет все свойства случайной последовательности чисел в рамках решаемой задачи.
Хотя псевдослучайная последовательность в этом смысле часто, как может показаться, лишена закономерностей, однако, любой псевдослучайный генератор с конечным числом внутренних состояний повторится после очень длинной последовательности чисел. Это может быть доказано с помощью принципа Дирихле.
См. также
Смотреть что такое «Псевдослучайная последовательность» в других словарях:
псевдослучайная последовательность — Детерминированная функция, которая генерирует последовательность битов с качествами случайной последовательности. [[http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23]] Тематики защита информации EN pseudo random sequence … Справочник технического переводчика
псевдослучайная последовательность — pseudoatsitiktinė seka statusas T sritis automatika atitikmenys: angl. pseudo random sequence vok. Pseudozufallsfolge, f rus. псевдослучайная последовательность, f pranc. séquence pseudo aléatoire, f … Automatikos terminų žodynas
последовательность Года — Псевдослучайная последовательность, образуемая путем сложения по модулю 2 двух псевдослучайных последовательностей. [Л.М.Невдяев. Мобильная связь 3 го поколения. Москва, 2000 г.] Тематики мобильная связь EN Gold sequence … Справочник технического переводчика
Псевдослучайная двоичная последовательность — частный случай ПСП, в которой элементы принимают два возможных значения 0 и 1 (или 1 и +1 ). Постулаты Голомба Одна из первых формулировок некоторых основополагающих правил для статистических свойств периодических псевдослучайных… … Википедия
последовательность скачков — 06.01.36 последовательность скачков [ hop sequence]: Псевдослучайная последовательность частот, используемая передатчиком для скачкообразного переключения частоты канала связи при применении широкополосной модуляции с прыгающей частотой (FHSS).… … Словарь-справочник терминов нормативно-технической документации
псевдослучайная двоичная последовательность — (МСЭ T G.709/ Y.1331). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN pseudo random binary sequencePRBS … Справочник технического переводчика
последовательность частотных скачков — 06.01.35 последовательность частотных скачков [ frequency hop sequence]: Псевдослучайная двоичная последовательность, определяющая скачкообразные переключения частоты канала связи, используемая в системах с широкополосной модуляцией с прыгающей… … Словарь-справочник терминов нормативно-технической документации
Псевдослучайная двоичная последовательность — 1. Определенная последовательность двоичных чисел, корреляционные свойства которой близки к корреляционным свойствам ограниченного по уровню шума Употребляется в документе: ГОСТ Р 52593 2006 … Телекоммуникационный словарь
сверхдлинная последовательность с большой избыточностью — Псевдослучайная последовательность с повышенной имитостойкостью. Обычно такая последовательность формируется с помощью подбора скорости шифрованной последовательности намного более высокой, чем исходная. [Л.М. Невдяев. Телекоммуникационные… … Справочник технического переводчика
Псевдослучайные последовательности и их применение для защиты информации
Автор: Пользователь скрыл имя, 14 Октября 2011 в 15:49, реферат
Описание работы
В настоящее время сфера применения псевдослучайных последовательностей чрезвычайно широка. Они используются в таких областях, как статистическое моделирование, системы передачи информации, вероятностное тестирование, защита информации в ЭВМ и сетях и другие. При этом от свойств псевдослучайных последовательностей напрямую зависит качество получаемых результатов.
Работа содержит 1 файл
Министерство образования и науки Украины
Национальный технический университет
«Харьковский политехнический институт»
Кафедра автоматики и управления в технических системах
«Псевдослучайные последовательности и их применение для защиты информации»
В настоящее время сфера применения псевдослучайных последовательностей чрезвычайно широка. Они используются в таких областях, как статистическое моделирование, системы передачи информации, вероятностное тестирование, защита информации в ЭВМ и сетях и другие. При этом от свойств псевдослучайных последовательностей напрямую зависит качество получаемых результатов.
Качественные псевдослучайные последовательности, являясь по своей сути детерминированными, обладают тем не менее практически всеми свойствами реализаций истинно случайных процессов и успешно их заменяют, так как случайные последовательности чрезвычайно сложно формировать.
Настоящая работа посвящена в первую очередь обзору существующих типов псевдослучайных последовательностей, области их применений, рассмотрению генераторов таких последовательностей, ориентированных на использование в системах защиты информации от случайных и умышленных деструктивных воздействий. Также рассмотрены принципы построения генераторов, а также требования, которым они должны удовлетворять при использовании в системах защиты информации.
1 ОПИСАНИЕ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1.1 Основные аспекты псевдослучайных последовательностей (ПСП)
Последовательности случайных чисел широко используются в самых разных приложениях — от компьютерного программирования, имитационного моделирования и методов Монте-Карло до криптографии. При этом от свойств случайных последовательностей напрямую зависит качество получаемых результатов.
Известны несколько областей, где псевдослучайные последовательности используются в процессе решения задач. К таким областям относятся статистическое моделирование, системы передачи информации, вероятностное тестирование, защита информации в ЭВМ и сетях и другие. Для решения этих задач необходимо формировать определенные случайные процессы, вырабатывать огромные количества случайных чисел с самыми разнообразными свойствами.
Псевдослучайная последовательность (ПСП) — это последовательность чисел, которая была вычислена по некоторому определённому арифметическому правилу, но имеет все свойства случайной последовательности чисел в рамках решаемой задачи. Хотя псевдослучайная последовательность в этом смысле часто, как может показаться, лишена закономерностей, однако, любой псевдослучайный генератор с конечным числом внутренних состояний повторится после очень длинной последовательности чисел.
Псевдослучайные последовательности, хотя и генерируются детерминированным образом, обладают всеми свойствами случайных сигналов. Однако они выгодно отличаются от ортогональных последовательностей инвариантностью к временному сдвигу.
Практически все алгоритмы генерации псевдослучайных последовательностей обладают в той или иной мере различными недостатками, такими как слишком короткий период выходной последовательности, наличие корреляции между различными ее членами, неравномерное распределение, предсказуемость, недостаточная скорость, сложность реализации и т. д.
1) Количество «1» в каждом периоде должно отличаться от количества «0» не более, чем на единицу.
2) В каждом периоде половина серий (из одинаковых символов) должна иметь длину один, одна четверть должна иметь длину два, одна восьмая должна иметь длину три и т.д. Более того, для каждой из этих длин должно быть одинаковое количество серий из «1» и «0».
Последовательность, удовлетворяющая правилам 1-3 часто именуется «ПШ-последователъностъю», где ПШ обозначает «псевдо-шумовая». К анализируемой последовательности применяется широкий спектр различных статистических тестов для исследования того, насколько хорошо она согласуется с допущением, что для генерации использовался совершенно случайный источник.
1.2 Разновидности ПСП
Существует несколько видов ПСП, обладающих разными характеристиками. Говоря попросту, сегодня появились технические средства, способные «вывести» любой ансамбль последовательностей с заданными свойствами.
Такие последовательности обладают следующими свойствами:
1.2.2 Последовательности Голда
Последовательности Голда могут быть сгенерированы путем суммирования по модулю 2 двух М-последовательностей одинаковой длины. Результирующие Коды Голда имеют ту же самую длину как и исходные М-последовательности (рис 1.2).
В проекте WCDMA специфицированы три типа кодов Голда: первичный и вторичный ортогональные коды Голда (оба длиной 256 бит) и длинный код.
Ортогональные коды Голда создаются на основе m-последовательности длиной 255 бит с добавлением одного избыточного символа. Первичный синхрокод имеет апериодическую автокорреляционную функцию и используется для первоначального вхождения в синхронизм. Вторичный синхрокод представляет собой немодулированный ортогональный код Голда, который передается параллельно с первичным синхрокодом. Каждый вторичный синхрокод выбирается из 17 различных кодов Голда
Длинный код для прямого канала представляет собой фрагменты кода Голда длиной 40 960 чипов. Система связи на базе WCDMA асинхронна, и соседние базовые станции используют различные коды Голда (всего их 512), повторяемые каждые 10 мс. Асинхронный принцип работы базовых станций делает их независимыми от внешних источников синхронизации. Предполагается применять длинный код и в обратном канале, однако только в тех сотах, где не задействуется режим многопользовательского детектирования.
1.2.3 Последовательности Касами
Подробно о генераторах случайных и псевдослучайных чисел
Введение
Как отличить случайную последовательность чисел от неслучайной?
Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.
Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)
Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.
Уязвимости ГПСЧ
Линейный конгруэнтный ГПСЧ (LCPRNG)
Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.
Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].
Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений
Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.
Предсказание результатов линейно-конгруэнтного метода
Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.
Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.
Взлом встроенного генератора случайных чисел в Java
Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы
Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)
Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).
Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:
до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так
Вывод данной программы будет примерно таким:
Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.
И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));
И всё, мы успешно взломали ГПСЧ в Java.
Взлом ГПСЧ Mersenne twister в PHP
Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.
Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:
10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor
Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так
Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.
Область для взлома
Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.
Задание распределения для генератора псевдослучайных чисел
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.
Треугольное распределение
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.
Экспоненциальное распределение
Тесты ГПСЧ
Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.
Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.
В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.
5. Генерация случайных и псевдослучайных последовательностей
Зачем вообще нужно рассматривать вопрос о генераторах случайных и псевдослучайных последовательностей в криптографии? Ведь в руководстве но каждому компилятору описана функция, позволяющая генерировать случайные числа. Наверное, лучше не городить огород, а воспользоваться тем. что уже имеется?
Нет, не лучше. К сожалению, датчики «случайных» чисел, встроенные в компиляторы, не подходят для криптографических приложений, поскольку генерируемые ими числа недостаточно случайны. Надеяться породить нечто совершенно случайное на компьютере, который по своей природе является строго детерминированным устройством, по меньшей мере, безосновательно.
Самое лучшее, на что способен компьютер, — это сгенерировать псевдослучайную последовательность, которая хотя и выглядит случайной, но, на самом деле, таковой не является. Период псевдослучайной последовательности должен быть достаточно большим, чтобы ее подпоследовательность требуемой длины была апериодичной, т. е. имела период, совпадающий с ее длиной. Например, если нужна строка из миллиона случайных бит, то для ее порождения не стоит использовать генератор последовательностей, которые повторяются через каждые 65536 бит.
Псевдослучайная битовая последовательность должна, по возможности, не отличаться от по-настоящему случайной. Необходимо, чтобы в ней число единиц примерно совпадало с числом нулей, а половина всех «полосок» (подряд идущих идентичных компонентов последовательности) имела длину I. одна четвертая — длину 2, одна восьмая — длину 4 и т. д. Кроме только что перечисленных, существует еще ряд общепринятых тестов, которые позволяют проверить, действительно ли данная последовательность является псевдослучайной.
Созданию хороших генераторов псевдослучайных последовательностей уделяется достаточно большое внимание в математике. В настоящее время удается порождать последовательности с периодом порядка 2000—3000 бит. Проблема в том, что все генераторы псевдослучайных последовательностей при определенных условиях дают предсказуемые результаты и корреляционные зависимости. А это как раз то, чего ждут от псевдослучайных последовательностей криптоаналитики, чтобы предпринять эффективную атаку на криптосистемы, где эти последовательности используются.
Криптографически надежные псевдослучайные последовательности
По-настоящему случайные последовательности
Последовательность называется no-настоящему случайной, если ее нельзя воспроизвести. Это означает, что если запустить генератор по-настоящему случайных последовательностей дважды при одном и том же входе, то на его выходе получатся разные случайные последовательности. Основная трудность состоит в том, чтобы суметь отличить случайную последовательность от неслучайной. Если несколько раз зашифровать строку символов с помощью криптографического алгоритма, соответствующего ГОСТ 28147-89, то получится последовательность, очень напоминающая по-настоящему случайную. Чтобы доказать ее неслучайность, другого способа, кроме аренды АНБ соответствующих вычислительных мощностей и программы вскрытия. не существует. Однако вряд ли ваше предложение об аренде будет воспринято там всерьез.
CDMA: сигналы и их свойства
Когда-то проектирование CDMA-систем было скорее искусством, чем наукой.
Инженеры выбирали сигналы, применение которых должно улучшить основные характеристики систем (качество связи, помехоустойчивость), полагаясь лишь на свою интуицию. Поворотным моментом стало создание теории формирования, обработки и передачи сигналов. Она позволяет определить эффективность использования конкретного ансамбля (множества) сигналов, базируясь лишь на знании их авто- и взаимокорреляционных характеристик.
Базовые понятия
Кодовые последовательности, используемые в CDMA-системах для передачи сигнала, состоят из N элементарных символов (чипов). Каждый информационный символ сигнала складывается с одной N-символьной последовательностью, которая называется «расширяющей» (spreading sequence), поскольку «результирующий» сигнал излучается в эфир с преднамеренно расширенным спектром. Выигрыш в качестве связи зависит как от числа символов (длины) последовательности, так и от характеристик совокупности сигналов, в первую очередь – их взаимокорреляционных свойств и способа модуляции.
Длина последовательности. В отечественной литературе сигналы, база которых существенно больше единицы (B=TF>>1, где T – длительность элемента сигнала, F – полоса частот), обычно называются сложными. По отношению к исходному (информационному) сложный сигнал представляет собой шум с практически одинаковой спектральной плотностью мощности.
Известно, что чем сильнее «растянут» спектр сигнала в эфире, тем меньше его спектральная плотность. Благодаря этому свойству сигналы с большой базой могут применяться в «чужой» (уже занятой) полосе частот «на вторичной основе», оказывая на работающую там систему сколь угодно малое воздействие.
Характеристики. Вся совокупность кодовых последовательностей, используемых в CDMA, делится на два основных класса: ортогональные (квазиортогональные) и псевдослучайные последовательности (ПСП) с малым уровнем взаимной корреляции (рис. 1).
В оптимальном CDMA-приемнике поступающие на его вход сигналы, которые, по сути, представляют собой аддитивный белый гауссовский шум, всегда обрабатываются с помощью корреляционных методов. Поэтому процедура поиска сводится к нахождению сигнала, максимально коррелированного с индивидуальным кодом абонента. Корреляция между двумя последовательностями
Дабы получить выигрыш в качестве связи при использовании любого из способов корреляционной обработки, необходимо, чтобы ансамбль сигналов обладал «хорошими» автокорреляционными свойствами. Желательно, чтобы сигналы имели единственный автокорреляционный пик, иначе возможна ложная синхронизация по боковому лепестку автокорреляционной функции (АКФ). Заметим, что чем шире спектр излучаемых сигналов, тем уже центральный пик (основной лепесток) АКФ.
Пары кодовых последовательностей подбираются так, чтобы взаимная корреляционная функция (ВКФ) имела минимальное значение при их попарной корреляции. Это гарантирует минимальный уровень взаимных помех.
Следовательно, выбор оптимального ансамбля сигналов в CDMA сводится к поиску такой структуры кодовых последовательностей, в которой центральный пик АКФ имеет наибольший уровень, а боковые лепестки АКФ и максимальные выбросы ВКФ по возможности минимальны.
Ортогональные коды
В теории сигналов доказано, что предельно достижимое значение коэффициента взаимной корреляции определяется из условия
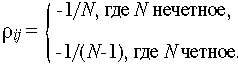 |
Минимальное значение ВКФ обеспечивает коды, у которых коэффициенты корреляции для любых пар последовательностей являются отрицательными (трансортогональные коды). Коэффициент взаимной корреляции ортогональных последовательностей, по определению, равен нулю, т.е. о?ij=0. При больших значениях N различием между коэффициентами корреляции ортогональных и трансортогональных кодов практически можно пренебречь.
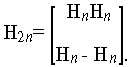 |
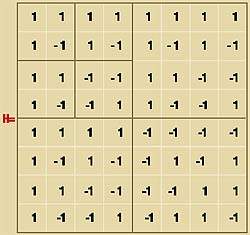 |
Принцип формирования этой матрицы достаточно прост; его поясняет рис. 2. Исходным является сигнал вида H1=<1>. Подставляя его в матрицу H2n, получаем новую матрицу большего размера:
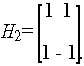 |
Многократное повторение процедуры позволяет сформировать матрицу любого размера, для которой характерна взаимная ортогональность всех строк и столбцов.
Такой способ формирования сигналов реализован в стандарте IS-95, где длина последовательностей Уолша выбрана равной 64. Заметим, что различие между строками матрицы Адамара и последовательностями Уолша состоит лишь в том, что в последних используются униполяные сигналы вида <1,0>.
Другая важная разновидность ортогональных кодов – биортогональный код, который формируется из ортогонального кода и его инверсии. Главное достоинство биортогональных кодов по сравнению с ортогональными – возможность передачи сигнала во вдвое меньшей полосе частот. Скажем, биортогональный блочный код (32,6), используемый в WCDMA, позволяет передавать сигнал транспортного формата TFI.
Отметим, что ортогональным кодам присущи два принципиальных недостатка.
1. Максимальное число возможных кодов ограничено их длиной (в стандарте IS-95 число кодов равно 64), а соответственно, они имеют ограниченное адресное пространство.
Для расширения ансамбля сигналов наряду с ортогональными используются квазиортогональные последовательности. Так, в проекте стандарта cdma2000 предложен метод генерации квазиортогональных кодов путем умножения последовательностей Уолша на специальную маскирующую функцию. Этот метод позволяет с помощью одной такой функции получить набор квазиортогональных последовательностей Quasi-Orthogonal Function Set (QOFS). С помощью m маскирующих функций и ансамбля кодов Уолша длиной 2 n можно создать (m+1) 2 n QOF-последовательностей.
2. Еще один недостаток ортогональных кодов (не исключение – и применяемые в стандарте IS-95) заключается в том, что функция взаимной корреляции равна нулю лишь «в точке», т.е. при отсутствии временного сдвига между кодами. Поэтому такие сигналы используются лишь в синхронных системах и преимущественно в прямых каналах (от базовой станции к абоненту).
Возможность адаптации системы CDMA к различным скоростям передачи обеспечивается за счет использования специальных ортогональных последовательностей с переменным коэффициентом расширения спектра (OVSF, Orthogonal Variable Spreading Factor), называемых кодами переменной длины. При передаче CDMA-сигнала, который создавался с помощью такой последовательности, чиповая скорость остается постоянной, а информационная скорость изменяется кратно двум. В стандартах 3-го поколения предлагается использовать в качестве OVSF-кодов ортогональные коды Голда с кратными скоростями передачи (multirate). Принцип их образования достаточно прост; его поясняет рис. 3, где приведено кодовое дерево, позволяющее строить коды разной длины.
 |
| Кодовое дерево для генерации OVS-кодов (SF – коэффициент расширения) |
Каждый уровень кодового дерева определяет длину кодовых слов (коэффициент расширения спектра, SF), причем на каждом последующем уровне возможное число кодов удваивается. Так, если на уровне 2 может быть образовано только два кода (SF=2), то на уровне 3 генерируются уже четыре кодовых слова (SF=4) и т.д. Полное кодовое дерево содержит восемь уровней, что соответствует коэффициенту SF=256 (на рисунке показаны лишь три нижних уровня).
Таким образом, ансамбль OVSF-кодов не является фиксированным: он зависит от коэффициента расширения SF, т.е. фактически – от скорости канала.
Следует отметить, что не все комбинации кодового дерева могут быть одновременно реализованы в одной и той же соте CDMA-системы. Главное условие выбора комбинации – недопустимость нарушения их ортогональности.
Псевдослучайные последовательности
Наряду с ортогональными кодами ключевую роль в CDMA-системах играют ПСП, которые хотя и генерируются детерминированным образом, обладают всеми свойствами случайных сигналов. Однако они выгодно отличаются от ортогональных последовательностей инвариантностью к временному сдвигу. Существует несколько видов ПСП, обладающих разными характеристиками. Говоря попросту, сегодня появились технические средства, способные «вывести» любой ансамбль последовательностей с заданными свойствами.
m-последовательности
Функция автокорреляции m-последовательности является периодической и двузначной:
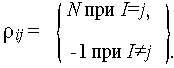 |
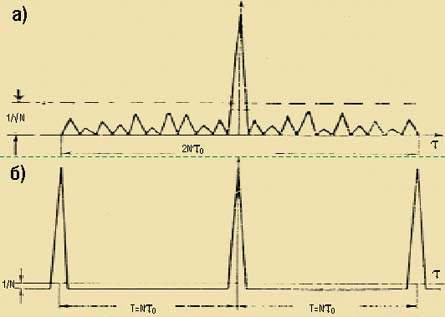 |
| Автокорреляционная функция для m-поседовательности: а) апериодическая, б) периодическая |
Уровень побочных максимумов автокорреляционной функции (рис. 4) не превышает значения
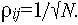 |
Коды Голда и Касами
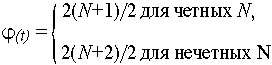 |
Коды Голда формируются путем посимвольного сложения по модулю 2 двух m-последовательностей (рис. 5). В проекте WCDMA специфицированы три типа кодов Голда: первичный и вторичный ортогональные коды Голда (оба длиной 256 бит) и длинный код.
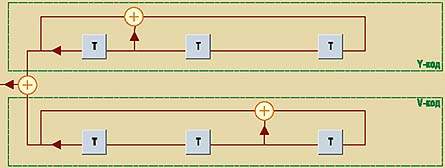 |
| Генератор кодов Голда (T – элемент регистра сдвига; & – схема совпадения; + – сумматор по модулю 2) |
Ортогональные коды Голда создаются на основе m-последовательности длиной 255 бит с добавлением одного избыточного символа. Первичный синхрокод имеет апериодическую автокорреляционную функцию и используется для первоначального вхождения в синхронизм. Вторичный синхрокод представляет собой немодулированный ортогональный код Голда, который передается параллельно с первичным синхрокодом. Каждый вторичный синхрокод выбирается из 17 различных кодов Голда
Длинный код для прямого канала представляет собой фрагменты кода Голда длиной 40 960 чипов. Система связи на базе WCDMA асинхронна, и соседние базовые станции используют различные коды Голда (всего их 512), повторяемые каждые 10 мс. Асинхронный принцип работы базовых станций делает их независимыми от внешних источников синхронизации. Предполагается применять длинный код и в обратном канале, однако только в тех сотах, где не задействуется режим многопользовательского детектирования.
Кодовые последовательности Касами реализуются с помощью трех последовательно включенных регистров сдвига (u, v и w) с различными обратными связями (рис. 6), каждый из которых формирует свою m-последовательность. Чтобы получить кодовые последовательности Касами с заданными свойствами, последовательности v и w должны иметь различные сдвиги.
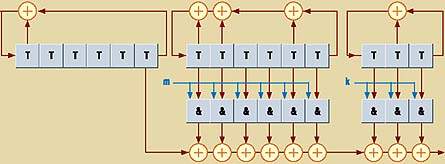 |
| Генератор кодов Касами типа kas (6, m, k), где m и k – циклические сдвиги v- и w-кодов соответственно (см. условные обозначения к рис. 5) |
Коды Касами длиной 256 бит используются в качестве коротких последовательностей в обратном канале (проект WCDMA) в тех сотах, в которых применяется многопользовательское детектирование.
Последовательности Баркера
Псевдослучайные последовательности с малым значением апериодической АКФ способны обеспечить синхронизацию передаваемых и принимаемых сигналов за достаточно короткий промежуток времени, обычно равный длине самой последовательности. Наибольшую известность получили последовательности Баркера (см. таблицу).
Эффективность последовательностей с апериодической АКФ принято оценивать показателем качества F, который определяется как отношение квадратов синфазных составляющих сигнала к сумме квадратов его расфазированных составляющих. Таким образом, мерой эффективности апериодической корреляции двоичной последовательности является показатель качества.
| N | Вид последовательности | Показатель качества |
| 7 | 1110010 | 9,85 |
| 11 | 11100010010 | 12,1 |
| 13 | 1111100110101 | 14,08 |
Поделитесь материалом с коллегами и друзьями
