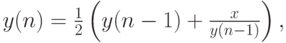что такое предусловие и постусловие
Что такое предусловие и постусловие
Циклический вычислительный процесс (ЦВП) характеризуется повторением одних и тех же вычислений над некоторым набором данных. Числом повторений цикла управляет специальная переменная, называемая его счетчиком или управляющей переменной цикла. На счетчик накладывается условие, определяющее, до каких пор следует выполнять цикл.
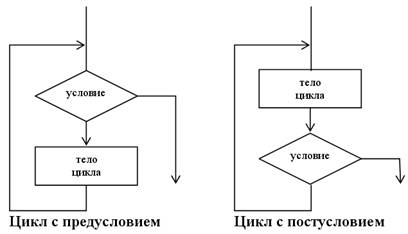
Рис. 9.1. Блок-схемы циклов с предусловием и постусловием
Для цикла с постусловием сначала выполняется тело цикла, затем управление передается на проверку условия. В зависимости от истинности или ложности условия, тело цикла выполняется повторно или же происходит переход к оператору, следующему за телом цикла. Всё, сказанное о возможном зацикливании для цикла с предусловием, справедливо и для цикла с постусловием.
Исходя из приведенных блок-схем, очевидно основное различие двух циклов: цикл с постусловием гарантированно выполняется хотя бы раз, а цикл с предусловием может не выполняться ни разу, если условие сразу же окажется ложным.
В языке Паскаль реализованы оба вида циклов. Цикл с предусловием имеет следующий общий вид:
while логическое_выражение do begin
Работу цикла можно описать словами: «пока логическое выражение истинно, повторяется тело цикла».
Логическое выражение строится по правилам, изученным в гл. 7. Тело цикла могут образовывать любые операторы Паскаля. Если в цикле находится всего один оператор, операторные скобки, показывающие начало и конец тела цикла, можно не писать.
Общая запись цикла с постусловием следующая:
так и с помощью repeat :
Зачастую использование одного из циклов выглядит предпочтительней. Например, обработка ввода пользователя с клавиатуры удобней с помощью repeat (сначала пользователь должен нажать клавишу, затем следуют проверки и обработка).
Принцип подстановки Барбары Лисков (предусловия и постусловия)
Почему у многих возникают проблемы с этим принципом? Если взять не «заумное», а более простое определение, то оно звучит так:
Наследующий класс должен дополнять, а не замещать поведение базового класса.
Звучит понятно и вполне логично, расходимся. но блин, как этого добиться? Почему-то многие просто пропускают информацию про предусловия и постусловия, которые как раз отлично объясняют что нужно делать.
В данной статье мы НЕ будем рассматривать общие примеры данного принципа, о которых уже есть много материалов (пример с квадратом и прямоугольником или управления термостатами). Здесь мы немного подробнее остановимся на таких понятиях как «Предусловия», «Постусловия», рассмотрим что такое ковариантность, контравариантность и инвариантность, а также что такое «исторические ограничения» или «правило истории».
Предусловия не могут быть усилены в подклассе
️Другими словами дочерние классы не должны создавать больше предусловий, чем это определено в базовом классе, для выполнения некоторого бизнес-поведения. Вот пример:
Добавление второго условия как раз является усилением. Так делать не надо!
К предусловиям также следует отнести «Контравариантность», она касается параметров функции, которые может ожидать подкласс.
Подкласс может увеличить свой диапазон параметров, но он должен принять все параметры, которые принимает родительский.
Этот пример показывает, как расширение допускается, потому что метод Bar->process() принимает все типы параметров, которые принимает метод в родительском классе.
Таким образом, мы не добавляем дополнительных проверок, не делаем условия жестче и наш дочерний класс уже ведёт себя более предсказуемо.
Постусловия не могут быть ослаблены в подклассе
️То есть подклассы должны выполнять все постусловия, которые определены в базовом классе. Постусловия проверяют состояние возвращаемого объекта на выходе из функции.
Условное выражение проверяющее результат является постусловием в базовом классе, а в наследнике его уже нет. Не делай так!
Сюда-же можно отнести и «Ковариантность», которая позволяет объявлять в методе дочернего класса типом возвращаемого значения подтип того типа (ШО?!), который возвращает родительский метод.
️Таким образом в дочернем классе мы сузили возвращаемое значение. Не ослабили. Усилили 🙂
Инвариантность
Здесь должно быть чуть проще.
Инварианты — это некоторые условия, которые остаются истинными на протяжении всей жизни объекта. Как правило, инварианты передают внутреннее состояние объекта.
Например типы свойств базового класса не должны изменяться в дочернем.
Здесь также стоит упомянуть исторические ограничения («правило истории»):
Подкласс не должен создавать новых мутаторов свойств базового класса.
Если базовый класс не предусматривал методов для изменения определенных в нем свойств, подтип этого класса так же не должен создавать таких методов. Иными словами, неизменяемые данные базового класса не должны быть изменяемыми в подклассе.
В таком случае стоит рассмотреть добавление мутатора в базовый класс.
Выводы
Даже не вникая в общие сложные абстрктные примеры самого принципа подстановки Барбары Лисков, а пользуясь этими, на мой взгляд, более простыми и более конкретными правилами, вы уже добьётесь более предсказуемого поведения дочерних классов.
Стоит упомянуть, что нужно страться избавляться от пред/пост условий. В идеале они должны быть определенны как входные/выходные параметры метода (например передачей в сигнатуру готовых value objects и возвращением конкретного валидного объекта на выход).
Управляющие операторы языка
Операторы цикла
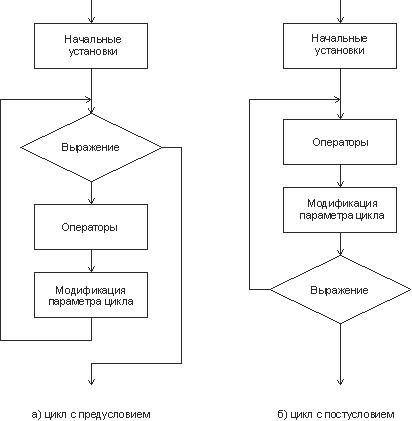
Блок, ради выполнения которого и организуется цикл, называется телом цикла. Остальные операторы служат для управления процессом повторения вычислений: это начальные установки, проверка условия продолжения цикла и модификация параметра цикла ( рис. 2.5). Один проход цикла называется итерацией.
Начальные установки служат для того, чтобы до входа в цикл задать значения переменных, которые в нем используются.
Проверка условия продолжения цикла выполняется на каждой итерации либо до тела цикла (тогда говорят о цикле с предусловием, см. рис. 2.5, а ), либо после тела цикла (цикл с постусловием, см. рис. 2.5, б ). Разница между ними состоит в том, что тело цикла с постусловием всегда выполняется хотя бы один раз, после чего проверяется, надо ли его выполнять еще раз. Проверка необходимости выполнения цикла с предусловием делается до тела цикла, поэтому возможно, что он не выполнится ни разу.
Цикл с предусловием while
Формат оператора прост:
while выражение do оператор
Пример. Программа, печатающая таблицу значений функции
для аргумента, изменяющегося в заданных пределах с заданным шагом.
Опишем алгоритм в словесной форме.
Цикл с постусловием repeat
Этот вид цикла применяется в тех случаях, когда тело цикла необходимо обязательно выполнить хотя бы один раз: например, если в цикле вводятся данные и выполняется их проверка.
Пример. Программа, вычисляющая квадратный корень вещественного аргумента X с заданной точностью eps по итерационной формуле:
где y ( n –1) — предыдущее приближение к корню (в начале вычислений выбирается произвольно), y ( n ) — последующее приближение. Процесс вычислений прекращается, когда приближения станут отличаться друг от друга по абсолютной величине менее, чем на eps — величину заданной точности ( пример 2.3)..
Проектирование по контракту: построение надежного ПО
Предусловия и постусловия
Класс стек
Этот пример даст возможность ознакомиться с практическим использованием утверждений. В предыдущей лекции была дана схема параметризованного класса «стек» в форме:
Реализация появится ниже. До рассмотрения проблем реализации важно отметить, что программы характеризуются строгими семантическими свойствами, не зависящими от специфики реализации. Например:
Такие свойства являются частью спецификации АТД, и даже люди далекие от использования любых формальных подходов неявно их понимают. Но в общих подходах к разработке ПО в программных текстах нельзя обнаружить следов спецификации. Предусловие и постусловие программы можно сделать явными элементами ПО. Так и поступим. Введем предусловие и постусловие как специальный вид объявлений с помощью ключевых слов require и ensure соответственно. Для класса «стек» это приведет к следующей записи, где временно оставлены пустые места для реализации:
Предусловия
Предусловия выражают ограничения, выполнение которых необходимо для корректной работы функции. Здесь:
Предусловия применяются ко всем вызовам программы, как внутри класса, так и у клиента. Корректная система никогда не вызовет программу в состоянии, в котором не выполняется ее предусловие.
Постусловия
Постусловие выражает свойство состояния, завершающего выполнение программы. Здесь:
Постусловие в программе выражает гарантию, представленную создателем программы, что выполнение программы завершается и приводит к состоянию с заданными свойствами, в предположении, что программа была запущена в состоянии, удовлетворяющем предусловию.
Постусловие программы put включает предложение:
Педагогическое замечание
Это зависит от того, что вы хотите. Можно рассматривать утверждения просто как комментарии, и тогда их нарушение не обнаруживается в период выполнения. Но их можно использовать для проверки того, что все идет по плану. Тогда во время выполнения окружение автоматически следит за выполнением утверждений и включает исключение при возникновении нарушений, завершая обычно выполнение и выводя сообщение об ошибке. Можно включить в программу обработку исключения, пытающуюся восстановить ситуацию и продолжить выполнение. Эта тема будет детально обсуждаться в следующей лекции. Для указания желаемой политики используются параметры компиляции, которые можно установить независимо для каждого класса.
Все детали мониторинга утверждений периода выполнения появятся чуть позже в этой лекции. Но было бы ошибкой на данном этапе уделять им много внимания. Другие аспекты утверждений сейчас важнее. Мы еще только приступили к рассмотрению этой техники, предназначенной, прежде всего, для создания корректного ПО; нам еще нужно многое открыть в их методологической роли встроенных стражей надежности. Вопрос о том, что случится, если возникнет ошибка, тоже важен, но рассматривать его следует после того, как мы сделаем все, чтобы предотвратить ее появление.
Циклы
Введение. Циклы с предусловием.
П ри решении практических задач постоянно возникает необходимость в повторении действия заданное количество раз, или до достижения какого-либо условия. Например, вывести список всех пользователей, замостить плоскость текстурой, провести вычисления над каждым элементом массива данных и т.п. В си для этих целей используются три вида циклов: с предусловием, постусловием и цикл for со счётчиком (хотя, это условное название, потому что счётчика может и не быть).
Рассмотрим цикл с предусловием.
Очень важно, чтобы условие выхода из цикла когда-нибудь выполнилось, иначе произойдёт зацикливание, и программа не завершится. К примеру
В этом цикле не изменяется переменная i, которая служит для определения условия останова, поэтому цикл не завершится.
В этой программе цикл, конечно, завершится, но из-за неправильного действия он будет выполнен гораздо больше 10 раз. Так как си не следит за переполнением переменной, нужно будет ждать, пока переменная переполнится и станет меньше нуля.
У этого примера неопределённое поведение. Так как переменная i заранее не инициализирована, то она хранит мусор, заранее неизвестное значение. При различном содержимом переменной i будет меняться поведение.
Если тело цикла while содержит один оператор, то фигурные скобки можно опустить.
Здесь мы инкрементируем переменную i при вызове функции printf. Следует избегать такого стиля кодирования. Отсутствие фигурных скобок, особенно в начале обучения, может приводить к ошибкам. Кроме того, код читается хуже, да и лишние скобки не сильно раздувают листинги.
Циклы с постусловием.
Ц икл с постусловием отличается от цикла while тем, что условие в нём проверяется после выполнения цикла, то есть этот цикл будет повторён как минимум один раз (в отличие от цикла while, который может вообще не выполняться). Синтаксис цикла
Предыдущий пример с использованием цикла do будет выглядеть как
Давайте рассмотрим пример использования цикла с постусловием и предусловием. Пусть нам необходимо проинтегрировать функцию.
∫ a b f ⁡ x d x = ∑ i = a b f ⁡ i h
Для нахождения интеграла необходимо пройти от a до b с некоторым шагом h, и прибавлять к сумме площадь прямоугольника со сторонами f(x) и h.
Программа выводит 0.328.
∫ 0 1 x 2 d x = x 3 3 | 0 1 = 1 3 ≈ 0.333
Если посмотреть на график, то видно, что каждый раз мы находим значение функции в левой точке. Поэтому такой метод численного интегрирования называют методом левых прямоугольников. Аналогично, можно взять правое значение. Тогда это будет метод правых прямоугольников.
Сумма в этом случае будет равна 0.338. Метод левых и правых прямоугольников не очень точен. Мы фактически аппроксимировали (приблизили) гладкий график монотонно возрастающей функции гистограммой. Если немного подумать, то аппроксимацию можно проводить не только суммируя прямоугольники, но и суммируя трапеции.
Приближение с помощью трапеций на самом деле является кусочной аппроксимацией кривыми первого порядка (ax+b). Мы соединяем точки на графике с помощью отрезков. Можно усложнить, соединяя точки не отрезками, а кусками параболы, тогда это будет метод Симпсона. Если ещё усложнить, то придём к сплайн интерполяции, но это уже другой, очень долгий разговор.
Вернёмся к нашим баранам. Рассмотрим 4 цикла.
Если выполнить эти примеры, то будет видно, что циклы выполняются от двух, до четырёх раз. На это стоит обратить внимание, потому что неверное изменение счётчика цикла часто приводит к ошибкам.
Часто случается, что нам необходимо выйти из цикла, не дожидаясь, пока будет поднят какой-то флаг, или значение переменной изменится. Для этих целей служит оператор break, который заставляет программу выйти из текущего цикла.
Давайте решим простую задачу. Пользователь вводит числа до тех пор, пока не будет введено число 0, после этого выводит самое большое из введённых. Здесь есть одна загвоздка. Сколько чисел введёт пользователь не известно. Поэтому мы создадим бесконечный цикл, а выходить из него будем с помощью оператора break. Внутри цикла мы будем получать от пользователя данные и выбирать максимальное число.
В этом случае мы выходим из цикла с помощью break; Для начала в качестве максимального задаём 0. Пользователь вводит число, после чего мы проверяем, ноль это или нет. Если это не ноль, то сравниваем его с текущим максимальным.
Бесконечные циклы используются достаточно часто, так как не всегда заранее известны входные данные, либо они могут меняться во время работы программы.
Когда нам необходимо пропустить тело цикла, но при этом продолжить выполнение цикла, используется оператор continue. Простой пример: пользователь вводит десять чисел. Найти сумму всех положительных чисел, которые он ввёл.
Вот ещё один пример. Необходимо, чтобы пользователь ввёл целое число больше нуля и меньше 100. Пока необходимое число не будет введено, программа будет продолжать опрос.
Цикл for
О дним из самых используемых является цикл со счётчиком for. Его синтаксис
Например, выведем квадраты первых ста чисел.
Одним из замечательных моментов цикла for является то, что он может работать не только с целыми числами.
Этот цикл выведет числа от 5.3 до 0.1. Цикл for может не иметь некоторых «блоков» кода, например, может отсутствовать инициализация, проверка (тогда цикл становится бесконечным) или изменение счётчика. Вот пример с интегралом, реализованный с применением счётчика for
Давайте рассмотрим кусок кода
Его можно изменить так
Более того, используя оператор break, можно убрать условие и написать
кроме того, используя оператор «,», можно часть действий перенести
ЗАМЕЧАНИЕ: несмотря на то, что так можно делать, пожалуйста, не делайте так! Это ухудшает читаемость кода и приводит к трудноуловимым ошибкам.
Возьмём точку на кривой с координатами (x; f(x)), сдвинемся на шаг h вперёд, получим точку (x+h, f(x+h)), тогда производная будет
То есть, отношение малого приращения функции к малому приращению аргумента. Внимательный читатель может задать вопрос, почему мы двигаемся вперёд по функции, а не назад. Ну пойдёмте назад
Возьмём среднее от этих двух значений, получим
В общем-то теперь задача становится тривиальной: идём от точки a до точки b и находим минимальное значение производной, а также точку, в которой производная принимает это значение. Для решения нам понадобятся, как и в задаче с интегралом, переменные для границ области поиска a и b, текущее значение x и шаг h. Кроме того, необходимо максимальное значение maxVal и координата maxX этого максимального значения. Для работы возьмём функцию x • sin ⁡ x
На выходе программа выдаёт max value = 1.391 at 1.077
Численное решение даёт такие же (с точностью до погрешности) результаты, что и наша программа.
Вложенные циклы
Рассмотрим пример, где циклы вложены друг в друга. Выведем таблицу умножения.
В этом примере в первый цикл по переменной i вложен второй цикл по переменной j. Последовательность действий такая: сначала мы входим в цикл по i, после этого для текущего i 10 раз подряд осуществляется вывод чисел. После этого необходимо перейти на новую строку. Теперь давайте выведем только элементы под главной диагональю
Как вы видите, оператор break позволяет выйти только из текущего цикла. Этот пример может быть переписан следующим образом
В данном случае мы используем во вложенном цикле счётчик первого цикла.