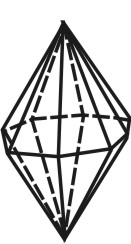
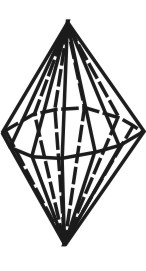
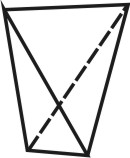
в какой сингонии возможна простая форма октаэдр
Сингонии
Сингонии в кристаллах
Кристаллографические классы, или виды симметрии, объединяются в более крупные группировки, называемые системами или сингониями. Таких сингоний семь:
1) кубическая — высшая категория
2) гексагональная средняя категория
3) тетрагональная средняя категория
4) тригональная средняя категория
5) ромбическая низшая категория
6) моноклинная низшая категория
7) триклинная низшая категория
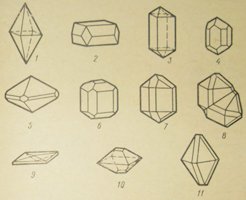
Рис. 22. Кристаллы кубической сингонии:
1- куб(пирит, торианит, галенит, флюорит, перовскит); 2- кубооктаэдр (галенит); 3- октаэдр (золото, хромит, пикотит, магнетит, шпинель); 4- ромбододекаэдр (золото, гранит, магнетит); 5- тетрагон триоктаэдр (гранит); 6- комбинация двух тетраэдров (сфалерит); 7- пентагон додекаэдр (пирит, гранат); 8-гексоктаэдр (алмаз); 9-двойник прорастания куба (пирит, торианит, флюорит)
В каждую сингонию входят кристаллы, у которых отмечается одинаковое расположение кристаллографических осей и одинаковые элементы симметрии. Сингонией называется группа видов симметрии, обладающих одним или несколькими одинаковыми элементами симметрии и имеющих одинаковое расположение кристаллографических осей.
Охарактеризуем каждую сингонию.
Высшая категория
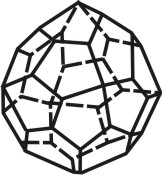
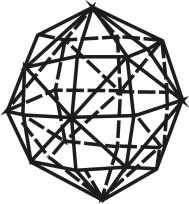
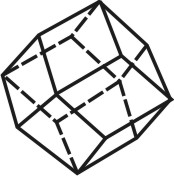
Кристаллы кубической сингонии встречаются в виде куба, октаэдра, тетраэдра, ромбододекаэдра, пентагон-додекаэдра и др. (рис. 22). В кубической сингонии кристаллизуются следующие минералы: каменная соль (галит), пирит, галенит, флюорит и др.
Рис. 23 Кристаллы гексагональной сингонии:
1- гексагональная дипирамида (кварц, корунд); 2- комбинация призмы и дипирамиды (кварц); 3- гексагональная призма (берилл, апатит); 4- комбинация призмы с дипирамидой и пинакоидом (апатит)
Сингонии средней категории
Эта группа объединяет Кристаллы, обладающие только одной осью симметрии порядка выше второго. К средней категории относятся гексагональная, тетрагональная и тригональная сингонии.
Гексагональная сингония характеризуется наличием одной оси симметрии шестого порядка (L 6 ). Максимальное количество элементов симметрии может быть следующим: L 6 6L 2 7PC. Кристаллы гексагональной сингонии образуют призмы, пирамиды, дипирамиды и др. (рис. 23). В гексагональной сингонии кристаллизуются апатит, нефелин, берилл и другие минералы.
Тетрагональная сингония имеет одну ось четвертого порядка (L 4 ). Максимальная симметрия для этой сингонии характеризуется формулой L 4 L 2 5РС. Формы кристаллов данной сингонии — тетрагональные призмы, пирамиды, дипирамиды и их комбинации (рис. 24). К тетрагональной сингонии относятся касситерит (оловянный камень), халькопирит (медный колчедан), циркон и другие минералы.
Рис. 24. Кристаллы тетрагональной сингонии:
1 — тетрагональная дипирамида (анатаз, циркон, ксенотим); 2 — анатаз; 3 — комбинация тетрагональной призмы с дипирамидой (циркон, брукит); 4 — комбинация дипирамиды и двух призм (ксенотим, рутил, циркон); 5 — комбинация двух призм с дипирамидой (везувиан, циркон); 6 — комбинация двух тетрагональных призм и дипирамиды с пинакоидом (везувиан); 7— комбинация двух призм с двумя дипирамидами (касситерит); 8 — двойник касситерита;
9, 10 — вульфнит; 11— шеелит
Тригональная сингония характеризуется одной осью третьего порядка (L 3 ). Наибольшее количество элементов симметрии выражается формулой L 3 3L 2 3PC. Формы кристаллов — призмы, пирамиды, дипирамиды, их комбинации и др. (рис. 25). В данной сингонии кристаллизуются кварц, кальцит, гематит, корунд и др.
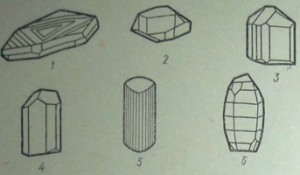
1- гематит; 2 — ильменит; 3, 4 —турмалин; 5 —кристалл турмалина со штриховкой на гранях; характерно поперечное сечение в форме сферического треугольника; 6 —корунд
Сингонии низшей категории
Кристаллы, в которых совсем отсутствуют оси симметрии высшего наименования и могут присутствовать только оси второго порядка (L 2 ), относятся к сингониям низшей категории. К ним относятся ромбическая, моноклинная и триклинная сингонии.

1 — ромбическая призма; 2 — ромбическая дипирамида; 3 — кристалл ставролита; 4-5— сросшиеся кристаллы ставролита в виде крестообразных двойников, 6 — комбинация призмы, пирамид и пинакоидов (олявин); 7 — комбинация двух призм и дипирамиды (топаз); 8-кристалл топаза; 9,10 —кристаллы арсенопирита; 11, 12 — кристаллы вядалузита; 13, 14 — колумбит-танталит; 15—самарскит
Ромбическая сингония имеет несколько осей второго порядка (L 2 ) или несколько плоскостей симметрии (Р). Характерные формы — ромбический тетраэдр, ромбическая призма, ромбическая пирамида и ромбическая дипирамида (рис. 26). Максимальная формула 3L 2 3PC. В ромбической сингонии кристаллизуются барит, топаз, марказит, антимонит и др.
Моноклинная сингония. Кристаллы моноклинной сингонии характеризуются наличием одной оси второго порядка (L 2 ) или одной плоскостью симметрии (Р), либо максимально: L 2 PC. Формы кристаллов — ромбическая призма и сочетание простых форм: пинакоидов и моноэдров (рис. 27). Характерные минералы моноклинной сингонии: ортоклаз, слюды, гипс, роговая обманка, пироксены и другие минералы.
Триклинная сингония.

Для определения сингонии неизвестного минерала по совокупности найденных найденных элементов симметрии пользуются таблицей 2. Иллюстрация определения сингонии кри-сталлов минимуму элементов симметрии приводится на рис. 29.
Рис. 27. Кристаллы моноклинной сингонии:
1 — комбинация трех пинакоидов; 2, 4 — кристаллы пироксена; 3 — комбинация призм и пинакоида (гипс, амфибол); 5, 6 — сфен; 7, 8—монацит; 9 — вольфрамит; 10, 11 — эпидот Простые формы и комбинации простых форм.
Открытые и закрытые формы
Природные многогранники — кристаллы— могут образовывать либо простые формы, либо их комбинации. Простой формой называется совокупность тождественных граней, связанных элементами симметрии. Грани такой простой формы должны быть одинаковыми по своим физическим и химическим свойствам, а в идеально развитых многогранниках — и по своим очертаниям и величине. Примерами простых форм могут служить куб, тетраэдр, октаэдр, ромбоэдр и т. д. Если кристалл образован несколькими видами граней, это комбинация нескольких простых форм. Комбинацией называется сочетание двух или нескольких простых форм, объединенных элементами симметрии. Насчитывается 47 простых форм известных в природе кристаллов (рис. 30).
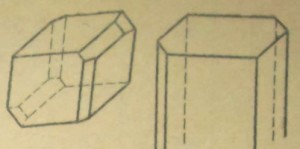
1—аксинит; 2—кианит
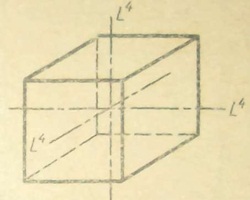
Рис. Кубическая средние сингонии (только одна ось высшего наименования)
Низшие сингонии (ни одной оси высшего наименования)
отнесения кристалла к
данной сингоний
Обязательно присутствуют:
симметрии
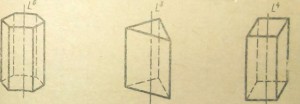
Рис. 29. Определение сингонии кристаллов:
Ромбическая, Моноклинная, Триклинная
Тритональная и гексагональная призмы и некоторый другие простые формы (например, тригональная и гексагональная пирамиды и др.) могут встречаться как среди тригональных, так и среди гексагональных кристалл.
Простые формы образуют великое множество комбинаций. Этим и объясняется то разнообразие геометрических форм, которое присуще природным многогранникам.
В кристаллографии в отличие от геометрии имеют дело не только с закрытыми, но и с открытыми формами. Если простая форма со всех сторон замыкает пространство, она называется закрытой. Например, куб, октаэдр, тетраэдр являются закрытыми простыми формами. Однако среди простых форм имеются и такие, которые неполностью замыкают пространство. Например, призмы, пирамиды. Такие формы называются открытыми.
Открытые формы могут существовать в кристалле только в сочетании с другими простыми формами, образуя комбинации простых форм. Так, например, кристалл в форме тригональной пирамиды (см. рис. 30) представляет сочетание двух простых форм — пирамиды и единичной грани — моноэдра, а кристалл в форме тригональной призмы слагают грани призмы и пинакоида (двух параллельных и равных граней).

Кристаллографическая номенклатура
В кристаллографической номенклатуре приняты кристаллографические термины, в основу которых положены греческие корни:
Кристаллографические сингонии
ЧТО ТАКОЕ КРИСТАЛЛОГРАФИЧЕСКИЕ СИНГОНИИ
Как указано выше, в кристаллах возможны 32 комбинации элементов симметрии, и эти 32 комбинации называют кристалло-графическими классами или видами симметрии. Кристаллографические классы объединяются в сингонии (или иначе системы) на основании некоторых признаков, из которых весьма важным является возможность при сходно выбранных координатных (кристаллографических) осях просто и рационально выразить символы граней. Таких сингоний выделяют 7.
Наименее симметричные кристаллические классы в количестве двух объединяются в триклинную сингонию, названную так, вследствие необходимости выбирать косоугольную систему кристаллографических осей, т. е. осей под тремя различными наклонами одна к другой. В ней или совсем нет элементов симметрии или имеется только центр симметрии. В этой сингонии кристаллизуются такие широко распространенные минералы, как плагиоклазы, также медный купорос и др.
Кристаллы, имеющие или одну плоскость симметрии (Р), или одну ось симметрии второго порядка (L 2 ), или и тот и другой элемент симметрии в сочетании с центром симметрии (L 2 Pc), относятся к моноклинной сингонии. Они могут быть рационально отнесены к системе координат, в которой только одна ось (I) образует косой угол с другой. В этой сингонии кристаллизуется очень много минералов: ортоклаз, авгит, а также сахар и ряд других веществ.
При наличии у кристаллов трех плоскостей симметрии и трех им перпендикулярных осей второго порядка и центра симметрии (3L 2 3Рс) кристаллы относятся к ромбической сингонии, так как в поперечном сечении они часто имеют форму ромба. К этой же сингонии относятся кристаллы с тремя осями симметрии второго порядка (3L 2 ) или с сочетанием двух плоскостей симметрии и осью второго порядка (L 2 2P).
Кристаллы с такой симметрией могут быть отнесены к системе трех взаимно-перпендикулярных осей координат.
В ромбической сингонии кристаллизуются сера, оливин, сурьмяный блеск и др.
К тетрагональной или квадратной сингонии относятся кристаллы, имеющие одну ось симметрии четвертого порядка простую или сложную (L 4 или Li4), единственную или в сочетании с другими элементами симметрии. При этом максимальная симметрия для этой сингонии может быть выражена формулой (L 4 4L 2 5Рс). К этой сингонии относятся кристаллы циркона, медного колчедана и др. (Кристаллы медного колчедана имеют симметрии Li42L 2 2Р, т. е. в их симметрии имеется сложная ось симметрии 4-го порядка).
Кристаллы, имеющие одну ось третьего порядка L 3 или Li — единственную или в сочетании с другими элементами симметрии, относятся к тригональной или ромбоэдрической сингонии и для рационального и простого обозначения граней должны относиться к четырехосной системе координат, причем ось L 3 принимается заIV ось, а три оси L 2 за I, II и III. Наибольшее количество элементов симметрии для этой сингонии выражается формулой L 3 3L 2 3Pc. Для тригональной сингонии имеются представители среди минералов: кварц, кальцит и др.
При наличии осей шестого порядка (L 6 или Li6) кристаллы относятся к гексагональной сингонии. Максимальное количество элементов симметрии, возможное для этой сингонии, выражается формулой L 6 6L 2 7Рс. Кристаллы относят к четырехосной системе координатных осей, причем ось L 6 принимается за IV ось, а три оси L 2 в тех случаях, когда они имеются, за оси I, II и III (рис. 10). При этом положительные направления этих осей принимаются через 120°, так что III ось своим отрицательным направлением обращена к наблюдателю. Подобный выбор осей позволяет изобразить символ грани четырьмя индексами, причем сумма трех первых индексов равна нулю. Например (1211) или (1010) и т. д. К этой сингонии относятся такие минералы, как апатит, нефелин и др.
Наиболее симметричными являются кристаллы кубической сингонии. Они обязательно должны иметь четыре оси третьего порядка (4L 3 ) и, кроме того, или три взаимно перпендикулярные оси четвертого порядка (3L 4 ) или вместо них три оси второго порядка (3L 2 ). Эти три оси выбираются за оси координат. Максимальное количество элементов симметрии в кубической сингонии отвечает виду симметрии 3L 4 4L 3 6L 2 9Рс. Таким образом кристаллы кубической сингонии являются наиболее симметричными из всех кристаллов. Представителями кубической сингонии являются: поваренная соль, алмаз, цинковая обманка, гранат и др.
ПРОСТЫЕ ФОРМЫ. КОМБИНАЦИИ. ДВОЙНИКИ
Е сли все грани кристалла тождественны между собой, т. е. выводятся все из одной благодаря имеющимся элементам симметрии, то такая форма кристалла называется прост ой формой.
Простую форму представляет собой, например, куб (рис. 11). Все шесть граней куба в идеально развитом кристалле тождественны между собой и представляют квадраты. Каждая грань куба пересекает одну координатную ось и параллельна двум другим. Символы граней куба (100), (010), (001), (100) и т. д.
Простые формы могут полностью замыкать пространство и тогда они носят название закрытых форм. Очевидно, что в этом случае весь кристалл будет представлен одной формой. Конечно, возможны и комбинации нескольких закрытых форм, но могут быть и такие формы, которые не замыкают пространства. Они называются открытыми и могут существовать в кристалле только в сочетании с другими формами, т. е. образовывать «комбинацию» с другими открытыми или закрытыми формами.
Наиболее важными простыми формами во всех сингониях, кроме кубической, будут:
1. Моноэдр — простая форма, состоящая из одной грани .
2. Диэдр — простая форма, состоящая из двух пересекающихся граней .
3. Пинакоид (от пинакс-доска) простая форма, состоящая из двух параллельных граней .
4. Призмы — простые формы, состоящие из трех или больше граней, пересекающихся по параллельным ребрам . Название призмам дается по виду поперечного сечения: ромбическая, гексагональная (6), тетрагональная (4), дитетра-гональная (8) и др.
5. Пирамиды — простые формы, состящие из трех или больше граней, пересекающихся в одной точке (табл. 2, 1—7). Называются пирамиды, так же как и призмы, по виду поперечного сечения ромбическая тригональная и т. д. Все указанные простые формы являются открытыми.
К закрытым формам относятся :
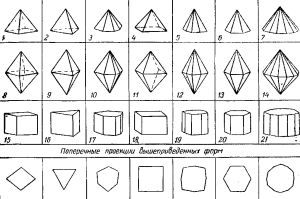
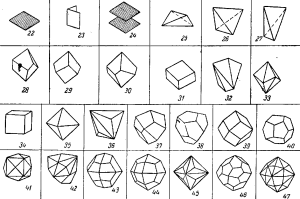
1—ромбическая пирамида; 2—тригональная пирамида; 3—дитригональная пирамида; 4—тетрагональная пирамида; 6—дитетрагональная пирамида; 6—гексагональная пирамида; 7 —дигексагональная пирамида; 8—ромбическая дипирамида; 9—тригональная дипирамида; 10—дитригональная дипирамида; 11—тетрагональная дипирамида; 12—дитетрагональная дипирамида; 13—гексагональная дипирамида; 14 — ли гексагональная дипирамида; 15-ромбическая призма; 16—тригональная призма; 17—дитригональная призма; 18— тетрагональная призма; 19—дитетрагональная призма; 20—гексагональная призма; 21—дигексагональная призма;
22—моноэдр: 23—диэдр; 24 — пинакоид; 25-ромбический тетраэдр; 26— тетраэдр; 27-тетрагональный тетраэдр; 28-тригональной трапецоэдр; 29—тетрагональный трапецоэдр; 30—гексагональный трапецоэдр 31—ромбоэдр; 32-тетрагональный скаленоэдр; 33—дитригональный скаленоэдр; 34—куб; 35—октаэдр; 36-григонтритетоаэдр; 37-тетрагонтритетраэдр; 33—пентагонтритетраэдр; 39- ромбдодекаэдр; 40—пентагондодекаэдр; 41— тетрагек-саэдр; 42—гексатетраэдр; 43—дидодекаэдр; 44—тетрагонтриоктаэдр; 45—тригонтриоктаэдр; 46— пентагонтриок таэдр; 47—гексаоктаэдр.
Статья на тему Кристаллографические сингонии
Похожие страницы:
Понравилась статья поделись ей
Кристаллография и кристаллохимия
Простые формы.
Формой многогранника называется совокупность всех его граней. Она определяется количеством всех сортов граней, взаимным расположением и соотношением размеров граней разного сорта. По внешнему виду кристаллы разделяются на две группы. К первой относятся такие кристаллы, которые состоят из одинаковых и симметрично расположенных граней (т.е. граней одного сорта). Они представляют собой простые формы. В простой форме все грани связаны между собой элементами симметрии и выводятся из одной заданной грани посредством этих элементов. Ко второй группе относятся кристаллы, обладающие различными по очертаниям и величине гранями (т.е. гранями разного сорта). Эти многогранники являются комбинациями, представляющими собой совокупность двух или нескольких простых форм. Количество простых форм, участвующих в сложении комбинационного многогранника, определяется количеством сортов граней. Всего известно 47 типов простых форм: 7 – для низшей категории, 25 – для средней и 15 – для высшей категории (таблица). Комбинаций возможно бесконечное количество.
Характеристика простых форм
Название простой формы
Число и расположение граней
Изображение простой формы
Две параллельные грани
Две пересекающиеся грани
Четыре попарно (через одну) параллельные грани
Четыре непараллельные грани, по три пересекающиеся в каждой вершине
Четыре грани, пересекающиеся в одной вершине
Восемь граней, располагающихся одна под другой, пересекающиеся в двух вершинах
Три параллельные грани, в сечении треугольник
Четыре параллельные (здесь и далее относительно главной оси) грани, в сечении квадрат
Шесть параллельных граней, в сечении шестиугольник
Шесть параллельных граней, в сечении дитригон (равносторонний шестиугольник, с углами, повторяющимися через один).
Восемь параллельных граней, в сечении дитетрагон (равносторонний восьмиугольник с углами, повторяющимися через один).
Двенадцать параллельных граней, в сечении дигексагон (равносторонний двенадцатиугольник с углами, повторяющимися через один.
Три равнонаклонные грани, пересекающиеся в одной точке на главной оси L 3.
Четыре равнонаклонные грани, пересекающиеся в одной точке на главной оси L 4.
Шесть равнонаклоненных граней, пересекающиеся в одной точке на главной оси L 6.
Шесть равнонаклоненных граней, пересекающихся в одной точке на главной оси L 3; в сечении дитригон.
Восемь равнонаклоненных граней, пересекающихся в одной точке на главной оси L 4, в сечении дитетрагон.
Двенадцать равнонаклоненных граней, пересекающихся в одной точке на главной оси L 6; в сечении дигексагон.
Шесть равнонаклоненных граней одна под другой, пересекающихся по три в точках на главной оси L 3 (две тригональные пирамиды, сложенные основаниями).
Восемь равнонаклоненных граней, одна под другой, пересекающиеся по четыре в двух точках на главной оси L 4 (две тетрагональные пирамиды, сложенные основаниями).
Двенадцать равнонаклоненных граней, одна под другой, пересекающихся по шесть в двух точках на главной оси L 6 (две гексагональные пирамиды, сложенные основаниями).
Двенадцать равнонаклоненных граней, располагающихся одна под другой, пересекающиеся в двух точках на главной оси L 3 (две дитригональные пирамиды, сложенные основаниями).
Шестнадцать равнонаклоненных граней, одна под другой пересекающихся по восемь в двух точках на главной оси L 4 (две тетрагональные пирамиды, сложенные основаниями).
Двадцать четыре равнонаклоненных грани, одна под другой, пересекающиеся по 12 в двух точках на главной оси L 6 (две дигексагональные пирамиды, сложенные основаниями).
Четыре непараллельных грани по три пересекающиеся в каждой вершине. Нижняя грань располагается симметрично между двумя верхними (и наоборот).
Шесть граней в виде ромба по три пересекающиеся в каждой вершине, нижняя грань расположена симметрично между двумя верхними (и наоборот).
Двенадцать наклонных граней, пересекающих по шесть в двух точках на главной оси L 3, нижняя пара граней расположенных симметрично между двумя парами верхних.
Восемь наклонных граней, пересекающихся по четыре в двух точках на главной оси Li 4; нижняя пара граней располагается симметрично между двумя парами верхних.
Шесть наклонных граней, пересекающихся по три в двух точках на главной оси L 3; нижние грани располагаются несимметрично относительно двух верхних.
Восемь наклонных граней, пересекающихся по четыре в двух точках на главной оси L 4; нижние грани располагаются несимметрично относительно двух верхних.
Двенадцать наклонных граней, пересекающихся по шесть в двух точках на главной оси L 6; нижние грани расположены несимметрично относительно двух верхних.
Четыре непараллельные грани, по три пересекающихся в каждой вершине.
Двенадцать наклонных граней по три усложняющих каждую грань тетраэдра.
Двенадцать наклонных граней по три усложняющих каждую грань тетраэдра.
Двенадцать наклонных граней по три усложняющих каждую грань тетраэдра.
Двадцать четыре грани, по шесть усложняющих каждую грань тетраэдра.
Восемь наклонных граней по четыре пересекающихся в каждой вершине.
Двадцать четыре наклонных грани по три усложняющие каждую грань октаэдра.
Двадцать четыре наклонных грани по три усложняющих каждую грань октаэдра.
Двадцать четыре наклонных грани по три усложняющих каждую грань октаэдра.
Сорок восемь граней по шесть усложняющих каждую грань октаэдра.
Шесть вертикальных и горизонтальных граней.
Двадцать четыре грани по четыре усложняющих каждую грань гексаэдра.
Двенадцатигранник из восьми наклонных, пересекающихся по четыре в двух точках, и четырех вертикальных граней.
Двенадцать наклонных граней, пересекающихся по три в каждой вершине.
Двадцать четыре грани по две усложняющие каждую грань пентагон-додекаэдра.
Простые формы бывают открытыми и закрытыми. Закрытая форма может одна образовывать кристаллический многогранник, так как грани закрытой формы полностью замыкают заключенное между ними пространство. К ним относятся дипирамиды, тетраэдры, трапецоэдры и др. Одна открытая простая форма, которыми являются, например, диэдры, пинакоиды, пирамиды и призмы, замкнутого многогранника образовать не может. Кристалл в этих случаях сформирован гранями нескольких простых форм, дающих комбинацию (не исключено, что в комбинации могут входить и закрытые формы).
Некоторые простые формы имеют две разновидности: правую и левую. Например, ромбические тетраэдры, все трапецоэдры, пентагон-тритетраэдры и др. Комбинационные многогранники также бывают правые и левые. Такие формы называют энантиоморфными (противоположно равными), это две зеркально равные фигуры, не совместимые друг с другом путем переносов и поворотов. Энантиоморфные формы возможны только в тех видах симметрии, в которых отсутствуют инверсионные оси, плоскости симметрии и центр инверсии.