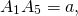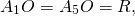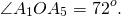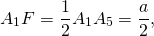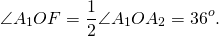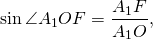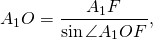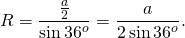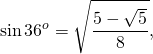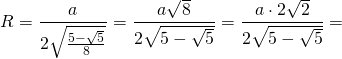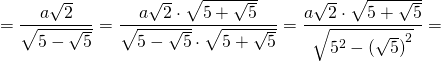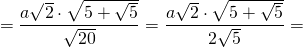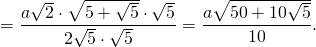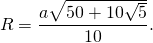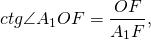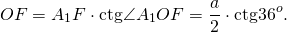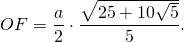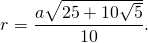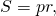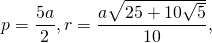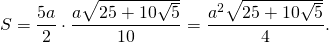в какой пятиугольник можно вписать окружность
Вписанные многоугольники
В основном курсе геометрии доказывается, что около всякого треугольника можно описать окружность. Оказывается, для четырехугольников это уже не имеет место.
Теорема 5. Около четырехугольника можно описать окружность, тогда и только тогда, когда сумма его противоположных углов равна 180°.
Теорема 6. В выпуклый четырехугольник можно вписать окружность, тогда и только тогда, когда суммы его противоположных сторон равны.
Теорема Птолемея для четырехугольника, вписанного в окружность, утверждает, что произведение его диагоналей равно сумме произведений противоположных сторон. Мы докажем более сильную теорему.
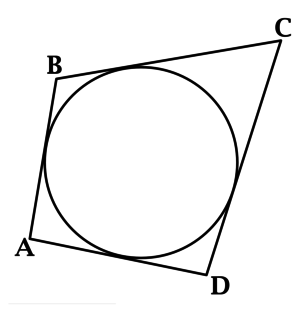
Теорема 7. Произведение диагоналей произвольного четырехугольника меньше или равно сумме произведений его противоположных сторон, причем равенство достигается только в случае четырехугольника, вписанного в окружность.
Пусть точки B, C и D переходят соответственно в точки B’, C’ и D’. Тогда треугольники ABC и A’C’B’, ADC и AC’D’, ABD и AD’B’ подобны и, следовательно, имеют место равенства
Складывая почленно эти равенства, получим
Следовательно, имеет место неравенство
При этом, равенство достигается только в случае, когда точки B’, C’, D’ принадлежат одной прямой. Это выполняется только в случае, если точки B, C, D принадлежат окружности, проходящей через точку A.
Рассмотрим теперь пятиугольники, вписанные в окружность.
Теорема 8. Сумма любых двух несмежных углов вписанного пятиугольника больше 180°.
Доказательство следует из того, что углы A и C пятиугольника ABCDE опираются на дуги, в сумме составляющие всю окружность плюс дугу DE (рис. 22).
Пример такого пятиугольника легко построить. Возьмем какой-нибудь вписанный пятиугольник ABCDE (рис. 23) и, продолжая две его стороны, построим пятиугольник ABCD’E’ так, чтобы сторона D’E’ была параллельна DE. Тогда углы этого пятиугольника будут равны углам исходного, и около него нельзя описать окружность.
Прежде чем ответить на этот вопрос выразим углы между диагоналями вписанного пятиугольника ABCDE, выходящими из одной вершины через углы самого пятиугольника.
Вернемся теперь к поставленному вопросу. Для ответа на него рассмотрим какую-нибудь окружность и разделим ее на дуги, равные удвоенным углам между диагоналями исходного пятиугольника, выходящим из одной вершины. Концы этих дуг будут вершинами искомого пятиугольника вписанного в окружность.
Таким образом, имеет место следующая теорема.
Теорема 9. Для произвольного пятиугольника ABCDE, суммы любых двух несмежных углов которого больше 180°, существует пятиугольник A’B’C’D’E’ с такими же углами, около которого можно описать окружность.
Ситуация с вписанными в окружность семиугольниками, девятиугольниками и т. д. аналогична рассмотренной ситуации с пятиугольниками.
Для вписанных многоугольников с четным числом сторон ситуация аналогична ситуации с вписанным четырехугольником.
Признак вписанного пятиугольника?
ТРЕБУЕТСЯ численно определить:
Можно ли вписать этот пятиугольник в окружность? И не забыть о погрешности (. )
РЕШЕНИЕ
Логика, интуиция, здравый смысл, размышления.
1. А что значит вписать пятиугольник в окружность? Ну во-первых видимо предполагается существование этой самой окружности. Причём в единственном числе. Допустим мы нашли такую окружность, то какими свойствами должен обладать наш пятиугольник? Понятно, что знание углов нашего пятиугольника нам мало что даст. (?)
2. Это почему мало?!
Если пятиугольник вписан в окружность, то мы можем разбить его на четырёхугольники, которые тоже будут вписаны в эту же окружность и применить указанный выше признак вписанного многоугольника с чётным числом сторон. Вот углы и пригодятся. Вообще потребуется провести расчёты для двух четырёхугольников, чтобы охватить все пять вершин. Сосчитать можно, но сложно.
3. Но почему бы нам не поступить иначе? Возьмём середину стороны и проведём к ней перпендикуляр. Если пятиугольник вписанный, то все пять перпендикуляров пересекутся в одной точке. С известной погрешностью конечно. А по-моему хватит и двух перпендикуляров. останется только проверить на равенство расстояния от этой точки до вершин пятиугольника. А погрешность? это ещё обдумать надо.
4. Есть ещё один численный метод. Ведь графику ещё не отменили. Рисуем наш пятиугольник, определяем на глазок (или с помощью простейших построений) центр окружности и далее пусть компьютер считает расстояния до вершин пятиугольника и погрешность тоже
5. Несколько слов о погрешности.
Как определить погрешность? Видимо есть несколько альтернативных способов, зависящих от метода решения задачи. А есть ли в данном случае некий общий критерий? Сие мне не ведомо! А хотелось бы узнать. Кто это знает?
В данной задаче я применил следующий критерий:
Программа находит из некоторого центра пять расстояний до вершин нашего пятиугольника. Вот разность между большим расстоянием и меньшим расстоянием и стала критерием. Программа выдала ответ, что центр окружности имеет координаты (370; 252) с абсолютной погрешностью 1,15.
ВОПРОС
Кто может прокомментировать всё выше сказанное? Буду рад, как частным высказываниям относительно этой задачи, так и общим суждениям в решении этой или подобной ей задаче.
примечание
Если бы многоугольник имел ось симметрии, то с вычислительной точки зрения задача была бы на порядок проще.
Точное построение фигуры
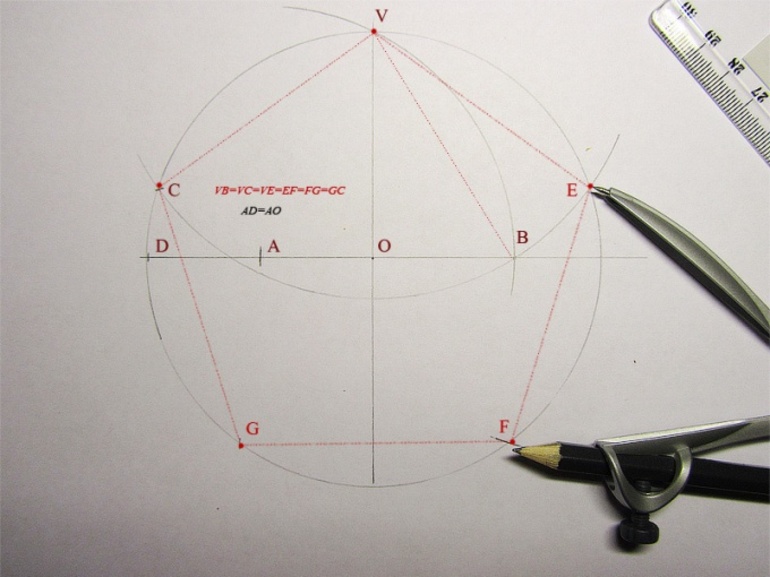
Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:
Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:
Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.
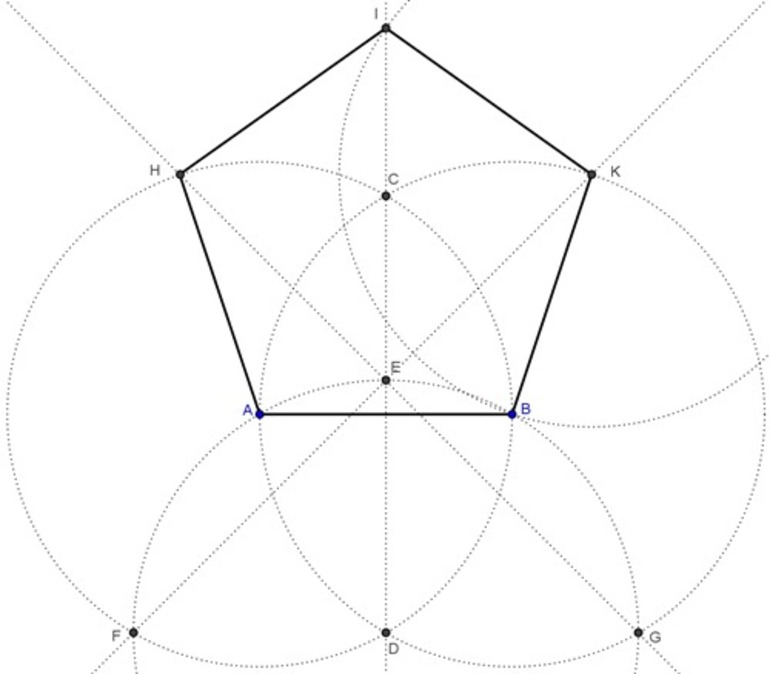
Алгоритм Биона
Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:
Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.
Приближенные методы
Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).
Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:
Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.
Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.
Признаки и свойства
Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:
Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:
Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.
Расчет параметров
С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.
Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.
Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.
Условные обозначения
Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:
Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2. Диагонали — отрезки, проведенные из одной вершины к противоположной (несмежной).
Соотношения и формулы
После обозначений следует переходить к рассмотрению основных формул, при помощи которых можно вычислять параметры фигуры. Сторону можно найти, воспользовавшись такими соотношениями:
Радиус вписанной окружности в пентагон можно найти, используя тригонометрические функции. Однако существует также формула, позволяющая вычислить приближенное значение. Это необходимо в том случае, когда под рукой нет специального онлайн-калькулятора, компьютера или таблиц Брадиса. Формулы для нахождения радиуса вписанной окружности:
Математики также рекомендуют описать вокруг пентагона окружность. Это расширит возможности по поиску его основных характеристик. Однако ее радиус следует вычислить. Формулы для его нахождения выглядят таким образом:
Периметр определяется просто: Р = 5а. Значение полупериметра эквивалентно половине периметра, то есть p = P / 2 = 5a / 2 = 2,5a. Площадь можно найти, используя такие формулы:
Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.
Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).
Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.
Окружность, вписанная в многоугольник или угол
Окружность называется вписанной в выпуклый многоугольник/угол, если она касается всех сторон этого многоугольника/угла.
Тогда многоугольник/угол называется описанным около окружности.
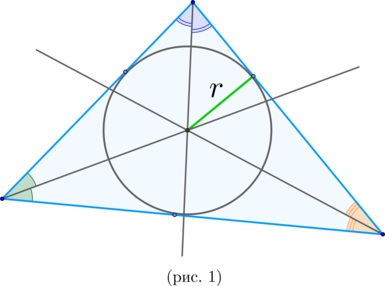
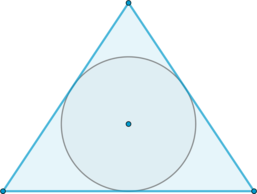
\(\blacktriangleright\) В любой треугольник можно вписать окружность. Ее центр лежит на пересечении биссектрис треугольника (рис. 1).
Площадь описанного треугольника ищется по формуле \[<\Large
где \(p\) – полупериметр.
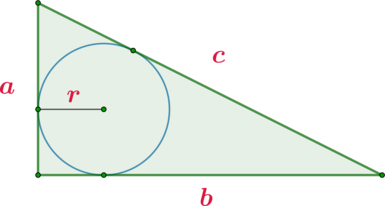
\(\blacktriangleright\) Если в прямоугольный треугольник вписана окружность, \(a, b\) – катеты, \(c\) – гипотенуза, \(r\) – радиус этой окружности, то верна формула: \[<\large
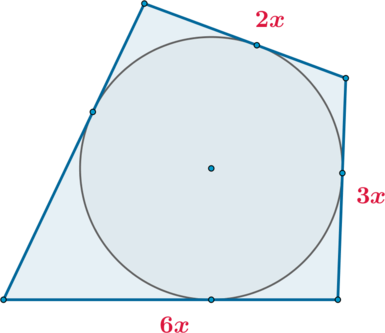
\(\blacktriangleright\) Если в выпуклый четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
И наоборот: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность (рис. 2).
Центр вписанной окружности лежит на пересечении биссектрис углов.
Площадь описанного четырехугольника ищется по формуле
где \(p\) – полупериметр.
\(\blacktriangleright\) Если в параллелограмм вписана окружность, то он – ромб (рис. 3).
\(\blacktriangleright\) Если в прямоугольник вписана окружность, то он – квадрат (рис. 4).
\(\blacktriangleright\) Если в угол вписана окружность, то ее центр лежит на биссектрисе этого угла (рис. 5).
Т.к. центр вписанной окружности лежит на пересечении биссектрис углов треугольника, то \(AO, BO\) – биссектрисы углов \(A, B\) соответственно.
На этапе подготовки к ЕГЭ старшеклассники повторяют базовые определения и формулы, в том числе и по теме «Окружность, вписанная в многоугольник или угол». Достаточно подробное изучение данного раздела планиметрии осуществляется, как правило, в средней школе. В связи с этим необходимость повторения основных формул и понятий по теме «Окружность, вписанная в угол или многоугольник» на этапе подготовки к ЕГЭ возникает у многих выпускников. Поняв принцип решения подобных заданий, старшеклассники смогут рассчитывать на получение достаточно высоких баллов по итогам сдачи единого государственного экзамена.
Готовьтесь к ЕГЭ вместе с образовательным порталом «Школково»
Занимаясь перед прохождением аттестационного испытания, многие старшеклассники сталкиваются с проблемой поиска базовых понятий и формул для нахождения радиуса окружности, вписанной в правильный многоугольник, и других параметров. Далеко не всегда их легко найти в Интернете, как и, например, задачи на правильный шестиугольник. А школьного учебника может просто не оказаться под рукой в нужное время. Для того чтобы ликвидировать пробелы в знаниях по этому и другим математическим разделам, обратитесь к образовательному проекту «Школково». На нашем сайте представлен весь необходимый материал, изложенный доступно и понятно. Какими свойствами обладает окружность, вписанная в угол и многоугольник, и какие формулы необходимо знать для успешного решения задач по данной теме? Ответы на эти и другие вопросы вы найдете на сайте «Школково» в разделе «Теоретическая справка».
Чтобы подготовка к единому госэкзамену была действительно эффективной, рекомендуем также попрактиковаться в решении соответствующих задач. Большая база заданий представлена в разделе «Каталог». Для каждого упражнения наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень задач на сайте постоянно дополняется и обновляется.
Правильный пятиугольник
По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна
∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).
Каждый центральный угол правильного пятиугольника, например, угол A1O A2, равен
Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.
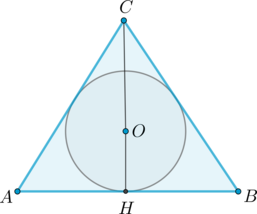
Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.
Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.

По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A1OA5, то есть
Рассмотрим прямоугольный треугольник A1OF.
Таким образом, формула радиуса описанной около правильного пятиугольника окружности —
Подставив значение котангенса 36°, получаем:
Итак, формула радиуса вписанной в правильный пятиугольник окружности
можно найти площадь правильного пятиугольника. Здесь
Все диагонали правильного пятиугольника равны.