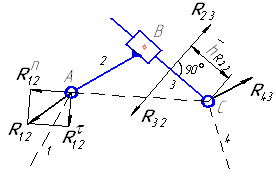
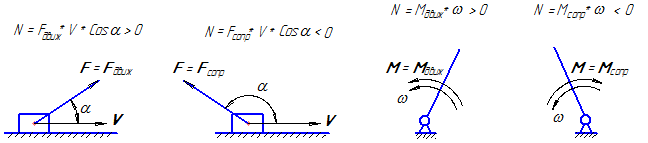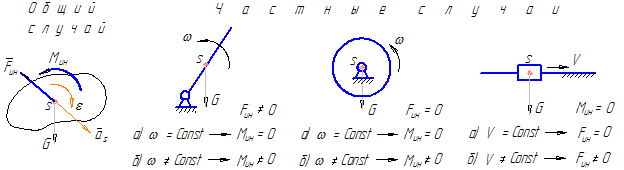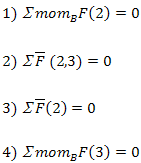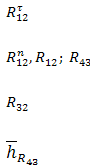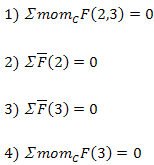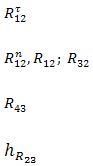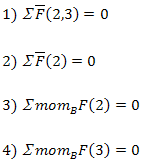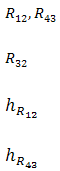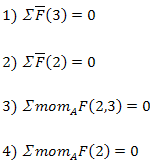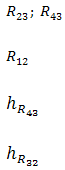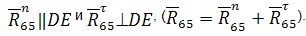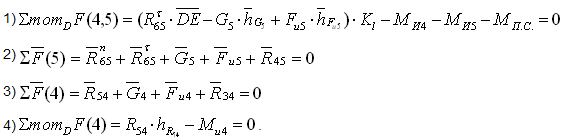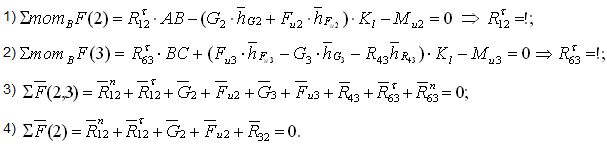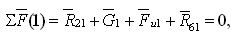в какой последовательности выполняется силовой расчет механизма

Рис. 17

6. Силовой расчет плоских механизмов

без учета сил трения

При работе механизма под действием внешних сил звенья механизма взаимодействуют и в кинематических парах его возникают силы реакции, которые в процессе движения могут измеряться по величине и направлению.

Целью силового расчета механизма является определение сил, действующих на звенья данного механизма при заданном движении его ведущего звена.

Способы определения внешних сил, а именно сил сопротивления, движущих сил, сил веса и сил инерции, рассмотрены в предыдущих параграфах, при этом для определения этих сил необходимо знать движение звеньев механизма. Поэтому, чтобы произвести силовой расчет механизма, при заданном движении ведущего звена, нужно произвести кинематическое исследование механизма. Определив ускорение и скорости движения звеньев, а также сил полезных сопротивлений если они зависят от скорости движения или перемещения рабочего звена.

Очевидно, что для определения сил инерции требуется знать размеры, массы и моменты инерции звеньев. Если механизм только проектируется и этих данных нет, то

приходится предварительно задаваться ориентировочными формами и весами их масс и моментов инерции, а в последующих расчетах уточнить принятие значения.

Таким образом, задача енотового расчета механизма может быть поставлена в следующем виде.

1) схема механизма и основные размеры всех его звеньев;

2) внешние силы, действующие на звенья (силы веса, силы полезного сопротивления, силы инерции). Если эти силы еще требуется определить, то, как сказано выше, необходимо дополнительно знать закон движения ведущего звена, массы и моменты инерции звеньев для определения внешних сил.

1) реакции во всех кинематических парах;

2) уравновешивающую силу или момент на ведущем валу.

Под уравновешивающим моментом (или силой), приложенным к ведущему звену в рабочей машине, понимают тот момент, который должен быть приложен со стороны двигателя к машине, чтобы при данном движении механизма преодолевались сопротивления всех внешних сил, действующих на механизм.

Под уравновешивающим моментом в машине- двигателе понимают момент сил сопротивления, приложенный к ведущему звену механизма, который может преодолеваться движущими силами, действующими на механизм двигателя.

Последовательность силового расчета механизма без учета сил трения

Силовой расчет механизмов производят сначала без учета сил трения, так как они, как правило, невелики. Однако в некоторых случаях они имеют существенное значение. Способы определения сил трения в кинематических парах и учет сил трения в механизмах с низшими парами будут освещены в последующей главе.

Силовой расчет механизма без учета сил инерции называется статическим. Такой расчет производится в тех случаях, когда силы инерции невелики, это бывает при малых массах звеньев и в тихоходных машинах.

Силовой расчет механизма называется динамическим, если при расчете учитываются силы инерции звеньев механизма.

Учет сил инерции особенно важен в быстроходных машинах, где иногда инерционные нагрузки на звенья достигают значений в десятки и сотни паз больше чем веса самих звеньев.

Последовательность силового расчета механизма без учета сил трения.

Силовой расчет механизма производится в определенной последовательности.

Рассмотрим эту последовательность расчета на примере механизма, приведенного на рис. 18,а.

Пусть на звенья механизма действуют известные внешние силы P₁, P₂, P₃, P₄. Требуется определить реакции во всех кинематических парах механизма и уравновешивающий момент M_y на кривошипе АВ, получаемый от двигателя, как необходимый движущий момент.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Последовательность силового расчета

1. Определяют главные вектора и главные моменты сил инерции звеньев.

2. Механизм разбивают на структурные группы Ассура и начальный механизм.

3. Проводят силовой расчет каждой группы Ассура. Вычисления выполняют в последовательности, соответствующей отбрасыванию структурных групп при структурном анализе по Ассуру.

Для составления уравнений равновесия группы Ассура для каждого звена зарисовывают расчетную схему, на которой показывают все внешние силы, силы реакций в кинематических парах, главный вектор и главный момент сил инерции.

Вовращательной КП составляющие силы реакции направляют в положительную сторону осей координат.

В поступательной КП выбирают положительное направление нормали к поверхности соприкосновения звеньев. Главный вектор распределенной реакции направляют в выбранную положительную сторону, главный момент – в положительном направлении против часовой стрелки.

Составляющие главного вектора сил инерции направляют в положительную сторону осей координат, а главный момент сил инерции – в положительном направлении против часовой стрелки.

Истинные направления неизвестных сил и моментов определяют по знакам величин, полученных в результате расчета.

4. Проводят расчет первичного механизма.

Пример силового расчета в система MathCAD

Исходные данные: схема механизма (рис.7.6),

Рис.7.6 Кривошипно-ползунный механизм

Определить: реакции в КП и уравновешивающий момент .

1. Определение главных векторов и главных моментов сил инерции звеньев:

2. Структурный анализ механизма по Ассуру.

3. Силовой расчет группы Ассура .

Для группы Ассура зарисовываем расчетную схему (рис. 7.7).

Рис.7.7. Расчетная схема для структурной группы .

Уравнения кинетостатики для звеньев 2 и 3 имеют вид:

, (7.3)

, (7.4)

. (7.5)

, (7.6)

, (7.7)

, (7.8)

Учитывая зависимости ,представляем уравнения кинетостатики (7.3) – (7.8) в матичной форме

, (7.9)

где – вектор неизвестных величин;

– вектор правой части системы линейных уравнений;

– матрица коэффициентов системы линейных уравнений.

В программе Mathcad решаем систему линейных уравнений (7.9) с помощью функции lsolve: .

4. Силовой расчет первичного механизма .

Вычисляем проекции силы : .

Зарисовываем расчетную схема для первичного механизма (рис. 7.8).

Рис. 7.8. Расчетная схема для первичного механизма

Уравнения кинетостатики для первичного механизма имеют вид:

, (7.10)

, (7.11)

, (7.12)

Представляем уравнения кинетостатики (7.10)–(7.12) в матричной форме

, (7.13)

где – вектор неизвестных величин;

– вектор правой части системы линейных уравнений;

– матрица коэффициентов системы линейных уравнений.

Решаем систему линейных уравнений (7.13) в Mathcad: .

Источник

iSopromat.ru

Силовой расчет механизмов относится к решению первой задачи динамики. Как видно из содержания задач динамики, приведенного выше, первая задача включает в себя две части: изучение сил, действующих на звенья механизма; определение неизвестных сил при заданном законе движения на входе (эта вторая часть и есть задача силового расчета).

В целях дальнейшего понимания терминологии и систематизации материала целесообразно повторить известные из физики и теоретической механики сведения о силах, а также ввести некоторые новые (применяемые в теории механизмов и машин) понятия. С точки зрения решения задач динамики силы (в данном случае под силой понимается обобщенное понятие силового фактора – собственно сила или момент) можно классифицировать следующим образом:

а) по взаимодействию звена механизма с другими объектами. По этому признаку силы подразделяются на внешние и внутренние:

б) по мощности, развиваемой силой. По этому признаку силы делятся на силы движущие и силы сопротивления (рисунок 16):

В свою очередь силы сопротивления можно разделить на силы полезного сопротивления и силы вредного сопротивления:

Работа по преодолению этих сил переводится в тепло и рассеивается в пространство, поэтому коэффициент полезного действия любого механизма всегда меньше единицы;

в) силы веса – это силы взаимодействия звеньев механизма с гравитационным полем земли;

г) силы трения – силы, сопротивляющиеся относительному перемещению соприкасающихся поверхностей;

д) силы инерции – силы, возникающие при неравномерном движении звена и сопротивляющиеся его ускорению (замедлению). Сила инерции действует на то тело, которое заставляет ускоряться (замедляться) данное звено. В общем случае при неравномерном движении возникает сила инерции и момент сил инерции:

где
F_ин – главный вектор сил инерции, приложенный в центре масс звена;
M_ин – главный момент сил инерции;
m – масса звена;
I_s – момент инерции звена относительно центра масс;
a_s – ускорение центра масс звена;
e – угловое ускорение звена.

Знак минус в формулах показывает, что сила инерции направлена противоположно ускорению центра масс звена, а момент сил инерции направлен противоположно угловому ускорению звена. Знак силы или момента учитывается только при установлении истинного направления силы или момента на расчетной схеме, а в аналитических вычислениях используется абсолютные их значения.

При силовом анализе механизмов могут встретиться различные случаи, когда один или оба силовых инерционных фактора могут иметь нулевое значение. На рисунке 17, приведенном выше, показаны некоторые случаи возникновения сил и моментов сил инерции при движении звеньев механизма.

Непосредственно силовой расчет сводится к определению неизвестных сил, действующих на звенья механизма. Как известно из теоретической механики для определения неизвестных сил используются уравнения статики.

Механизм же является неравновесной системой, т.к. большинство его звеньев имеет неравномерное движение, а точки, принадлежащие этим звеньям, движутся по сложным криволинейным траекториям (напомним: состояние равновесия – это состояние покоя или прямолинейного равномерного движения).

Поэтому для решения поставленной задачи применяется метод кинетостатики.

Метод кинетостатики основан на принципе Даламбера: если ко всем внешним силам, действующим на звенья механизма, добавить силы инерции и моменты сил инерции, то данный механизм будет находиться в состоянии статического равновесия. То есть это искусственный прием, приводящий неравновесную систему в состояние равновесия.

Искусственность приема заключается в том, что силы инерции прикладываются не к тем телам, которые заставляют двигаться звенья ускоренно (замедленно), а к самим звеньям.

Применив этот прием, в дальнейшем можно производить силовой расчет с использованием уравнений статики. Однако, чтобы решить задачу с помощью только уравнений равновесия, система должна быть статически определимой.

Условие статической определимости плоской кинематической цепи:

Для каждого звена, расположенного в плоскости, можно составить три независимых уравнения статики. Если в кинематической цепи имеется «n» подвижных звеньев, то в совокупности для этой цепи можно записать 3n независимых уравнений статики (равновесия). Эти уравнения используются для определения реакций в кинематических парах и неизвестных внешних сил.

На плоскости существуют кинематические пары только пятого и четвертого классов. Пары пятого класса представлены вращательной кинематической парой (шарниром) и поступательной парой (соединение ползуна с направляющей). В шарнире усилие между звеньями может передаваться в любом направлении, поэтому у реакции в шарнире неизвестными являются величина и направление (два компонента), т.е. для определения полной реакции во вращательной паре надо затратить два уравнения статики.

В первом приближении расчет ведется без учета сил трения. В этом случае перемещению ползуна вдоль направляющей ничто не препятствует. Перемещаться же поперек направляющей и поворачиваться ползун не может, поэтому в поступательной паре реакция направлена перпендикулярно направляющей и возникает реактивный момент, препятствующий повороту ползуна.

При силовом расчете обычно реактивный момент не определяют, а находят условную точку приложения реакции (произведение реакции на расстояние до ее условной точки приложения и есть реактивный момент). На определение реакции в поступательной паре также надо затратить два уравнения статики (определить два компонента – величину и точку приложения). Таким образом, на определение полной реакции в кинематической паре пятого класса необходимо затратить два уравнения статики.

Пары четвертого класса (высшие пары) на плоскости представляют соприкасающиеся между собой профили. В высшей паре усилие между звеньями передается по общей нормали к касающимся профилям (без учета сил трения). Поэтому в высшей паре четвертого класса реакция неизвестна только по величине (точка приложения реакции в точке контакта профилей, направление вдоль общей нормали к этим профилям).

Таким образом, для определения реакции в паре четвертого класса надо затратить одно уравнение статики (определить один компонент – величину реакции).

Если в кинематической цепи количество пар пятого класса равно Р₅, то на определение реакций во всех этих парах надо затратить 2Р₅ уравнений статики. На определение реакций во всех парах четвертого класса используется число уравнений, равное количеству этих пар Р₄.

Таким образом, из 3n независимых уравнений статики 2Р₅ уравнений используются для определения реакций в парах пятого класса и Р₄ – для определения реакций в парах четвертого класса. Оставшиеся уравнения используются для определения неизвестных внешних сил, действующих на звенья механизма.

Пусть X – число уравнений, оставшихся для определения неизвестных внешних сил, тогда

но эта формула совпадает с формулой Чебышева для определения числа степеней свободы плоской кинематической цепи. В результате можно сформулировать условие статической определимости кинематической цепи следующим образом: кинематическая цепь статически определима в том случае, когда число неизвестных внешних сил, действующих на ее звенья, не превышает числа степеней свободы этой цепи.

Так как методы решения разработаны для групп Ассура, то необходимо сформулировать условие статической определимости группы Ассура. Группа Ассура – это кинематическая цепь, имеющая собственную степень свободы, равную нулю. Поэтому группа Ассура статически определима, если на ее звенья не действуют неизвестные внешние силы.

Уравнений в группе Ассура достаточно лишь для определения реакций в кинематических парах. Это обстоятельство предопределяет порядок силового расчета механизма:

При таком подходе на группы Ассура всегда будут действовать только известные внешние силы и из рассмотрения их равновесия будут определены реакции в кинематических парах, а из рассмотрения условий равновесия начальных звеньев будут определены оставшиеся реакции и неизвестные внешние силы.

Поскольку решение ведется по группам Ассура, то ниже рассматривается принцип силового расчета групп на примере групп второго класса.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

В основу силового расчета механизмов по методу Н.Г. Бруевича положен принцип кинетостатики: если ко всем внешним действующим на звенья механизма силам добавить силы инерции и моменты сил инерции, то механизм будет находиться в состоянии статического равновесия.

Силовой расчет проводится по группам Ассура, начиная с наиболее удаленной от начального механизма. Заканчивается рассмотрением кривошипа, входящего в начальный механизм, для которого определяют уравновешивающую силу или уравновешивающий момент.

Для различных структурных групп Ассура разработаны специальные методы их силового исследования. В таблица 3 приведены рекомендации по анализу структурных групп II класса 1, 2, 3, 4, 5 видов.

Таблица 3 – Силовой анализ групп Ассура II класса

Заменить реакцию R₁₂ составляющимиСоставитьОпределитьгруппа 2 вида

Заменить реакцию R₁₂ составляющимиСоставитьОпределитьгруппа 3 вида

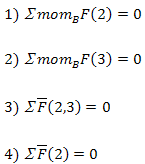
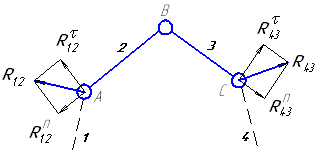
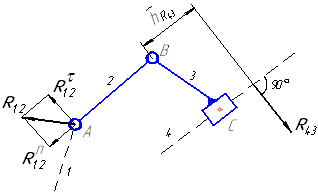
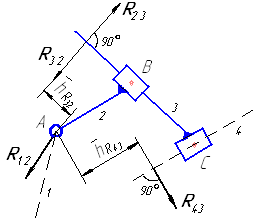
Рассмотрим последовательность силового расчета для заданного примера (рисунок 1). Все группы Ассура и кривошип начального механизма вычерчиваем отдельно (в масштабе) в том положении, которое они занимают на механизме в рассматриваемый момент времени.

Прикладываем к ним все силовые факторы, включая реакции в кинематических парах. Реакции во вращательных парах (шарнирах) неизвестны по величине и направлению, поэтому первоначально направляем их произвольно. Реакция в поступательной паре (ползуне) направлена перпендикулярно направляющей (т.к. вначале расчет ведется без учета сил трения), но неизвестны величина и точка приложения этой реакции.

Сила полезного сопротивления F_п.с. всегда направляется против скорости точки приложения этой силы, а момент сил полезного сопротивления М_п.с. – против угловой скорости звена приложения этого момента.

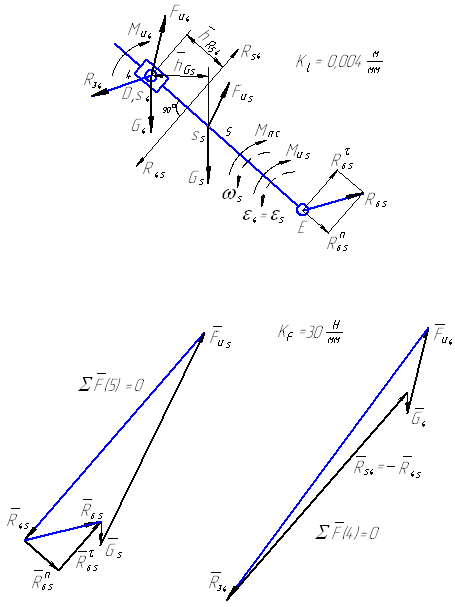
Группа (4,5) второго класса третьего вида

На звено 5 действует момент полезного сопротивления М_п.с., который направляется противоположно ω₅ в данном положении механизма (если звено 5 движется поступательно, то действует сила полезного сопротивления F_п.с., которая направлена против скорости этого звена).

Одну из крайних реакций (в данном примере R₆₅ в шарнире Е) раскладываем на две составляющие:

Рисунок 8 – К силовому расчету по методу Н.Г. Бруевича группы Ассура II класса 3 вида

Решая первое уравнение, определяем R τ ₆₅. Если реакция R τ ₆₅ получится отрицательной, значит ее фактическое направление противоположно предварительно принятому. Второе и третье уравнения решаются графически построением планов сил в выбранном масштабе K_l (рисунок 8).

При этом во втором уравнении неизвестными являются величины реакций R n ₆₅ и R₄₅ при известном их направлении (R n ₆₅||DE, R₄₅⊥DE). Пересечением этих векторов при построении плана получаем их величины. В третьем уравнении R₅₄=-R₄₅, а вектор R₃₄ неизвестен ни по величине, ни по направлению и при построении плана сил определяется как замыкающий вектор.

Решая четвертое уравнение, определяем точку приложения реакции R₅₄ (истинное значение плеча h_R54 в метрах).

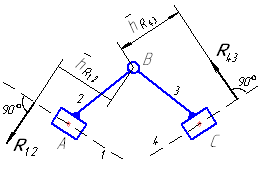
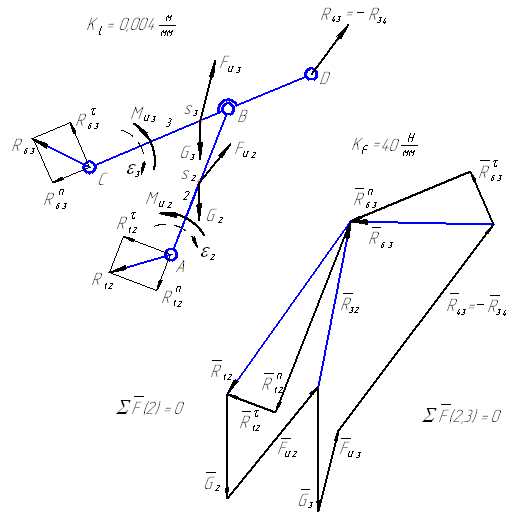
Группа (2,3) второго класса первого вида

Рисунок 9 – Кинетостатика группы Ассура II класса 1 вида (звенья 2 и 3)

При решении этой группы (рисунок 9) также составляем четыре уравнения равновесия, из которых определяем реакции в кинематических парах (шарнирах) А, В и С. Реакция в шарнире D является теперь известной внешней силой (R₄₃=-R₃₄). Графическая часть решения приводится на рисунке 9.

Примечание: в данном примере план сил, действующих на звено 2, для определения реакции R₃₂ представлен как часть общего плана для группы 2,3 (левая часть общего плана).

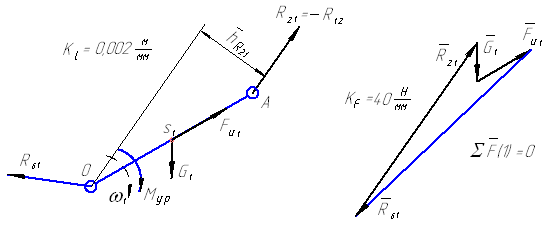
Завершаем силовой расчет по методу Н.Г. Бруевича рассмотрением равновесия кривошипа 1 (начальное звено анализируем последним). Для определения реакции R₆₁ строим план сил по уравнению

Из уравнения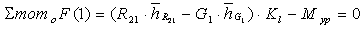

определяем уравновешивающий момент М_ур (в данном случае движущий момент, необходимый для преодоления всех сил, включая М_П.С., и обеспечивающий при этом заданный закон движения на входе ω ₁ = const).

Рисунок 10 – К кинетостатике кривошипа 1

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник