в какой последовательности сформирована конструкция ветвления
Информатика. 7 класс
Электронное приложение к учебному пособию
Напишите нам
белый — основные материалы, обязательные для изучения;
голубой — примеры, иллюстрирующие основные материалы;
желтый — определения основных понятий;
светло-зеленый — исторические сведения, информация об ученых, внесших вклад в развитие информатики, и другие интересные факты.
В учебном пособии используются следующие условные обозначения:




* — задание или пример для любознательных.
§ 12. Алгоритмическая конструкция ветвление
12.1. Команда ветвления
Довольно часто на поставленный вопрос человек получает ответ «да» или «нет». В зависимости от ответа он определяет свои действия и выполняет одну или другую команду (группу команд).
Роботы и другие технические устройства тоже могут выполнять различные действия в зависимости от условия. Если условие истинно (на вопрос получен ответ «Да»), то выполняются одни действия, если ложно, то другие.
Алгоритмическая конструкция ветвление обеспечивает выполнение одной или другой последовательности команд в зависимости от истинности или ложности некоторого условия.
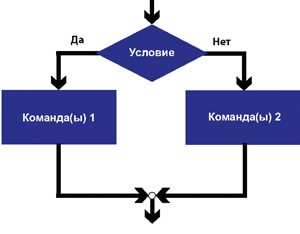
Ветвление может изображаться на блок-схеме следующим образом:
В данной конструкции в прямоугольнике(ах) записываются команды алгоритма. При такой организации алгоритма может выполниться только одна из двух команд (последовательностей команд). Другая последовательность будет проигнорирована (пример 12.1).
Строка if условие > then является заголовком ветвления. Эту строку можно прочитать следующим образом: «Если условие верно, то». После слова then записывается последовательность команд 1, которая выполнится, если условие истинно. После слова else записывается последовательность команд 2, которая выполнится, если условие ложно. Слова begin и end; в данном случае играют роль операторных скобок. Обратите внимание, что перед словом else точка с запятой не ставится.
Ветвление может быть записано в полной или сокращенной форме.
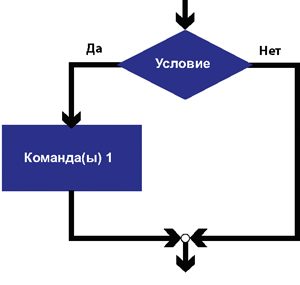
Полная форма ветвления предусматривает организацию выполнения двух разных наборов команд, из которых выполняется только один. В сокращенной форме один из наборов команд (чаще по ответу «Нет») опускается. В этом случае, если условие ложное, то никакие действия не выполняются.
На блок-схеме сокращенная форма ветвления изображается следующим образом:
На языке программирования Pascal команда запишется следующим образом:
Алгоритм может содержать более одной конструкции ветвления (пример 12.3).
Пример 12.4. Решим задачу if 1 из встроенного задачника.
Робот должен закрасить клетку, которая находится за стеной. В зависимости от обстановки обход стены может осуществляться по-разному.
Вначале Робот должен сдвинуться вправо. Если стена снизу, то сверху свободно и можно обойти стену сверху, в противном случае Робот обходит стену снизу.
После обхода стены Робот закрашивает клетку. Алгоритм можно записать следующим образом:
Если сверху свободно, то
Пример 12.5. Робот находится на неизвестной клетке поля без линий. Он должен закрасить клетку слева от себя.
Для того чтобы закрасить клетку слева от себя, Робот должен переместиться влево, а затем закрасить клетку. Однако сделать это Робот сможет только тогда, когда не находится в клетках, являющихся левой границей поля. Поэтому, прежде чем сдвинуться влево, Робот должен проверить, свободно ли слева.
Результат работы данной программы зависит от начального положения Робота. Поэтому для проверки правильности работы программы необходимо подготовить начальные обстановки, которые дают разные ответы на вопрос: слева пусто?
12.2. Составные условия
В качестве условия в алгоритмах с циклами и ветвлениями используется любое понятное исполнителю этого алгоритма высказывание, которое может быть либо истинным, либо ложным.
Все условия, с которыми нам приходилось до сих пор встречаться при составлении алгоритмов для Робота, были простыми высказываниями. Однако для исполнителя Робот можно строить и составные условия.
Составное условие — условие, которое образуется из нескольких простых условий, соединенных друг с другом логическими операциями.
С логическими операциями над высказываниями вы уже знакомы. В PascalABC используются следующие логические операции:
| Логическая операция | Запись в PascalABC |
| Не | Not |
| И | And |
| Или | Or |
Система условий для исполнителя Робот построена таким образом, что можно обойтись без использования логической операции отрицания.
Конструкция ветвления в C++
Конструкция ветвления в C++
Нередко возникают ситуации, в рамках которых программа вынуждена выбирать вид выполняемой операции опираясь на определенные условия.
Например, мы вводим какое-то целое число. Если оно >10, то программа приступает к выполнению одного действия, если 
Фигурными скобками обрамляется тело условия. В случае, если условие имеет шанс на выполнение, то и остальные команды, находящиеся в пределах фигурных скобок, также будут выполнены.
Пример конструкции ветвления
В данном случае подразумевается зависимость типа появляющегося сообщения от значения переменной num. Давайте попробуем усовершенствовать таким образом, чтобы добиться появления сообщения о num = 10.
Проверяем три условия при которых число или = 10.
Обратите внимание – во втором условии нами используется именно оператор равенства. Объясняется это тем, что значение переменной при проведении проверки нами не изменяется – мы просто проводим элементарное сравнение переменной с числом 10.
Если в условие интегрировать оператор усваивания, то при выполнении проверки этого условия, значение рабочей переменной будет изменено. В итоге условие успешно выполнится.
Каждому существующему оператору if может быть присвоен один-единственный оператор else. Объединение else if свидетельствует о том, что если более раннее условие не было успешно выполнено, то нужно проверить то условие, которое существует в данный момент. Если все условия неверны, то начинается выполнение тела else.
Если после трех вышеупомянутых операторов планируется выполнение одной-единственной команды, то от использования фигурных скобок можно отказаться. Что же касается предыдущей программы, то ее можно представить так:
Если нужно выполнить более одной команды, то постановка фигурных скобок обязательна:
В вышеприведенной программе выполняется проверка num. При значении
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 2.4. Основные алгоритмические конструкции
§ 2.4. Основные алгоритмические конструкции
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
Человеку в жизни приходится решать множество различных задач. Решение каждой из них описывается своим алгоритмом, и разнообразие этих алгоритмов очень велико. Вместе с тем для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения. Это положение выдвинул и доказал Э. Дейкстра в 70-х гг. прошлого века.
Эдсгер Вибе Дейкстра (1930-2002) — выдающийся нидерландский учёный, идеи которого оказали огромное влияние на развитие компьютерной индустрии.
2.4.1. Следование. Основные алгоритмические конструкции
Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными алгоритмами.
Графическое представление алгоритмической конструкции «следование» приведено на рис. 2.8.
Пример 1. Линейный алгоритм приготовления отвара шиповника.
Обратите внимание, что многие из предписаний этого алгоритма могут потребовать детализации — представления в виде некоторой совокупности более мелких предписаний.
Пример 2. У исполнителя Робот есть четыре команды перемещения (вверх, вниз, влево и вправо), при выполнении каждой из них Робот перемещается на одну клетку в соответствующем направлении. По команде закрасить Робот закрашивает клетку, в которой он находится. Запишем линейный алгоритм, исполняя который Робот нарисует на клетчатом поле следующий узор и вернётся в исходное положение, обозначенное звёздочкой:
Пример 3. Дан фрагмент линейного алгоритма:
Выясним, какое значение получит переменная s после выполнения этого фрагмента алгоритма. Для этого составим таблицу значений переменных, задействованных в алгоритме:
Составленная нами таблица значений переменных моделирует работу исполнителя этого алгоритма.
Пример 4. Некоторый исполнитель может выполнять над целыми ЧЧ0, числами кроме операций сложения, вычитания, умножения и деления ещё две операции: с помощью операции div вычисляется целое частное, с помощью операции mod — остаток.
Покажем, как с помощью этих операций можно реализовать алгоритм работы кассира, выдающего покупателю сдачу (s) наименьшим количеством банкнот по 500 (k500), 100 (k100), 50 (k50) и 10 (k10)рублей.
Исполните алгоритм для s = 745 и s = 1864. Составьте соответствующие таблицы значений переменных.
Ознакомьтесь с имеющимся в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Линейные алгоритмы» (217039). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
2.4.2. Ветвление. Основные алгоритмические конструкции
Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.
Блок-схема ветвления представлена на рис. 2.9. Каждая ветвь может быть любой степени сложности (рис. 2.9, а), а может вообще не содержать предписаний (рис. 2.9, б).
На алгоритмическом языке команда ветвления записывается так:
Для записи условий, в зависимости от результатов проверки которых выбирается та или иная последовательность действий, используются операции сравнения:
А В — А больше В;
А>=В — А больше или равно В;
А<>В — А не равно В.
Здесь буквы А и В можно заменять на любые переменные, числа и арифметические выражения. Приведённые операции сравнения допускаются и для символьных переменных.
Пример 7. Алгоритм вычисления функции ƒ(x) = |х| для произвольного числа х.
Обратите внимание на второй блок этой блок-схемы. В нём представлены имена и типы величин (данных), обрабатываемых в алгоритме.
Условия, состоящие из одной операции сравнения, называются простыми. В качестве условий при организации ветвлений можно использовать и составные условия. Составные условия получаются из простых с помощью логических связок and (и), or (или), not (не): and означает одновременное выполнение всех условий, or — выполнение хотя бы одного условия, a not означает отрицание условия, записанного за словом not.
Пример 8. Алгоритм определения принадлежности точки х отрезку [а, b]. Если точка х принадлежит данному отрезку, то выводится ответ ДА, в противном случае — НЕТ.
Существует достаточно много ситуаций, в которых приходится выбирать не из двух, а из трёх и более вариантов. Есть разные способы построения соответствующих алгоритмов. Один из них — составить комбинацию из нескольких ветвлений.
Пример 9. Алгоритм, в котором переменной У присваивается значение большей из трёх величин А, Б и С.
Пусть А = 10, В = 30 и С = 20. Тогда процесс выполнения алгоритма можно представить в следующей таблице:
Пример 10. Алгоритм решения линейного уравнения ах + b = 0.
Пример 11. Исполнитель Робот может выполнять ту или иную последовательность действий в зависимости от выполнения следующих простых условий:
| справа свободно слева свободно сверху свободно снизу свободно клетка чистая | справа стена слева стена сверху стена снизу стена клетка закрашена |
Также Робот может действовать в зависимости от выполнения составных условий.
Подумайте, в какую клетку переместится Робот из клетки, обозначенной звёздочкой, при выполнении следующего фрагмента алгоритма.
если справа свободно или снизу свободно
то закрасить
все
если справа стена
то влево
все
если слева стена
то вправо
все
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Алгоритмы с ветвящейся структурой» (217044). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
Повторение. Основные алгоритмические конструкции
Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию повторения, называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла.
В зависимости от способа организации повторений различают три типа циклов:
Цикл с заданным условием продолжения работы (цикл-ПОКА, цикл с предусловием)
Логика работы этой конструкции описывается схемой, показанной на рис. 2.10.
На алгоритмическом языке эта конструкция записывается так:
Выполняется цикл-ПОКА следующим образом: 1) проверяется условие (вычисляется значение логического выражения); 2) если условие удовлетворяется (Да), то выполняется тело цикла и снова осуществляется переход к проверке условия; если же условие не удовлетворяется, то выполнение цикла заканчивается. Возможны случаи, когда тело цикла не будет выполнено ни разу.
Пример 12. Алгоритм, по которому из всех имеющихся кирпичей отбираются целые кирпичи и складываются в машину.
алг отбор
нач
нц пока есть кирпичи
взять один кирпич
если кирпич целый
то положить кирпич в машину
иначе отложить кирпич в сторону
все
кц кон
Пример 13. Правее Робота (клетка со звёздочкой) расположен коридор неизвестной длины. Необходимо, чтобы Робот закрасил все клетки этого коридора.
Пока будет выполняться условие справа свободно, Роботу следует выполнять команды:
Соответствующий алгоритм для Робота будет иметь вид:
Пример 14. Требуется, не пользуясь операцией деления, получить частное q и остаток r от деления натурального числа х на натуральное число у.
Представим операцию деления как последовательные вычитания делителя из делимого. Причём вычитать будем до тех пор, пока результат вычитания не станет меньше вычитаемого (делителя). В этом случае количество вычитаний будет равно частному от деления q, а последняя разность — остатку от деления r.
Исполним этот алгоритм для х = 23 и у = 5.

Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с предусловием» (217033). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
Цикл с заданным условием окончания работы (цикл-ДО, цикл с постусловием)
Логика работы этой конструкции описывается схемой, показанной на рис. 2.11.
На алгоритмическом языке эта конструкция записывается так:
Выполняется цикл-ДО следующим образом: 1) выполняется тело цикла; 2) проверяется условие (вычисляется значение логического выражения); если условие не удовлетворяется («Нет»), то снова выполняется тело цикла и осуществляется переход к проверке условия; если же условие удовлетворяется, то выполнение цикла заканчивается. В любом случае тело цикла будет выполнено хотя бы один раз.
Пример 15. Алгоритм по выучиванию наизусть четверостишия.
алг четверостишие
нач
нц
прочитать четверостишие по книге 1 раз
рассказать четверостишие
кц при не сделал ошибку кон
Пример 16. Вычислим значение переменной b согласно следующему алгоритму:
Составим таблицу значений переменных, задействованных в алгоритме:
Пример 17. Спортсмен приступает к тренировкам по следующему графику: в первый день он должен пробежать 10 км; каждый следующий день следует увеличивать дистанцию на 10% от нормы предыдущего дня. Как только дневная норма достигнет или превысит 25 км, необходимо прекратить её увеличение и далее пробегать ежедневно ровно 25 км. Начиная с какого дня спортсмен будет пробегать 25 км?
Пусть х — количество километров, которое спортсмен пробежит в некоторый i-й день. Тогда в следующий (i + 1)-й день он пробежит х + 0,1х километров (0,1х — это 10% от х).
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с постусловием» (217037). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
Цикл с заданным числом повторений (цикл-ДЛЯ, цикл с параметром)
Логика работы этой конструкции описывается схемой, показанной на рис. 2.12.
На алгоритмическом языке эта конструкция записывается так:
нц для i от i1 до i2 шаг R
кц
В цикле-ДЛЯ всегда есть параметр цикла — величина целого типа, изменяющаяся в ходе выполнения цикла от своего начального значения il до конечного значения i2 с шагом R.
Выполняется цикл-ДЛЯ следующим образом: 1) параметру цикла присваивается начальное значение; 2) параметр цикла сравнивается с конечным значением; если параметр цикла не превышает конечное значение, то выполняется тело цикла, увеличивается значение параметра цикла на шаг и снова осуществляется проверка параметра цикла; если же параметр цикла превышает конечное значение, то выполнение цикла заканчивается.
Если величина шага в цикле с параметром равна единице, то шаг не указывают. Мы ограничимся рассмотрением именно таких циклов.
В отличие от двух предыдущих конструкций (цикл-ПОКА, цикл-ДО) цикл-ДЛЯ имеет строго фиксированное число повторений, что позволяет избежать зацикливания, т. е. ситуации, когда тело цикла выполняется бесконечно.
Пример 18. Алгоритм переправы через реку воинского отряда из пяти человек. Солдаты могут воспользоваться помощью двух мальчиков — хозяев небольшой лодки, в которой может переправиться или один солдат, или два мальчика.
алг переправа
нач
нц для i от 1 до 5
два мальчика переправляются на противоположный берег
один мальчик высаживается на берег, другой плывёт обратно
солдат переправляется через реку
мальчик возвращается на исходную позицию
кц
кон
Пример 19. Составим алгоритм вычисления степени с натуральным показателем n для любого вещественного числа а.
При составлении алгоритма воспользуемся единой формулой, в которой число умножений равно показателю степени:
Исполним этот алгоритм для а = 4 и n = 3.
Пример 20. Для исполнителя Робот цикл с известным числом повторений реализуется с помощью следующей конструкции:
Так, если правее Робота не встретится препятствий, то, выполнив приведённый ниже алгоритм, он переместится на пять клеток вправо и закрасит эти клетки:
алг
нач
нц 5 раз
вправо; закрасить
кц
кон
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с параметром» (217024). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
Основные алгоритмические конструкции. Самое главное
Для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения.
Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными.
Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.
Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию «повторение», называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла. В зависимости от способа организации повторений различают три типа циклов: