в каком классе проходят степени по математике
Степень числа. 5-й класс
Разделы: Математика
Класс: 5
Организация урока:
Закрепление понятия степени числа и научить применять ее свойства.
Ход урока
1. Организационный момент
2. Проверка домашнего задания:
Викторина “Герои произведения Гомера”
В ответе: получится имя божества-покровителя Одиссея.
О годы, вы так по-космически мчитесь,
Что трудно порой оглянуться назад:
Урок математики, школьный учитель,
Суровое слово и ласковый взгляд.
Ты с первого класса твердил нам,
Что можно любую на свете задачу решить.
Коль вычесть унынье, волю умножить,
Упорство прибавить, любовь разделить.
И в маленьких клеточках школьных тетрадей
Вставала и грела огромная жизнь,
В матросском десанте, в подпольном отряде,
Тревожной порой за нее мы дрались.
И каждый слова твои помнит, что можно
Любую на свете задачу решить.
Коль вычесть унынье, волю умножить,
Упорство прибавить, любовь разделить.
Стоим на рассвете у звездного старта
И видим, на миг оглянувшись назад,
Урок математики, школьную парту,
Суровое слово и ласковый взгляд.
Спасибо, учитель! Смогли мы и сможем
Любую на свете задачу решить.
Коль вычесть унынье, волю умножить,
Упорство прибавить, любовь разделить.
№ 753 (757),
754 (758),
749 (753).
Ищем педагогов в команду «Инфоурок»
Конспект урока в 7 классе по теме
« Возведение в степень произведения, частного и степени»
Цель урока: повторение и обработка навыков возведения в степень произведения, частного и степени
Закрепление правил по данной теме;
Формирование умений и навыков работы с возведением в степень.
Развитие познавательного интереса;
Развитие логического мышления, памяти, внимания, навыков работы в команде;
Привитие учащимся навыков самостоятельной работы;
Воспитание настойчивости в достижении цели;
Тип урока: у рок – повторения и обобщения.
Вид урока: урок – игра – учащиеся работают самостоятельно. Чтобы посадить самый красивый сад и преодолеть все трудности, которые встречаются на их пути, они должны вспомнить все, что изучалось по теме «Возведение в степень произведения, частного и степени».
Карточки в виде фруктов;
«Вкусив от сладкого плода математики, мы уподобляемся лотофагам, ибо воспользовавшись ею хоть раз, мы не хотим от нее оторваться, и она овладевает нами, как цветок лотоса». Аристотель
«Математика это орудие, с помощью которого человек познает мир и покоряет его». С. В. Ковалевская
Сообщение темы и цели
Игра «Математический сад».
П
Рисунок 6. Площадка для сада
Каждый участник вытягивают карточки – задания, на которых стоит номер фрукта или ягоды, который он должен вырастить. Если участник правильно выполняет задания, рассада фруктов и ягод приживается в саду. После выполнения он берет следующую карточку.
№ 11 – смородина, № 12 – крыжовник, № 13 – гранат, № 14 – малина, № 15 – виноград.
Не выполняя вычисления, сравните значения выражений:
а) (-0,03) 8 и 0 б) 0 и (-1,25) 9
Представьте в виде степени произведение:
a ) (- а ) 3 · в 3 б)
Ответ:а) 
Представьте в виде степени с основанием а :
а) 


Ответ: а) 


Найдите значение выражения:
а) 
Ответ: а) 
Ответ: а) 

Степень числа
Урок 20. Математика 5 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Степень числа»
Представим себе такую историю…
– И что это за число-то такое? – не мог понять Саша.
– Что случилось? – поинтересовался у друга Паша.
– Недавно я услышал, что человек состоит из клеток. И вот мне стало интересно, что это за клетки такие и сколько их в нашем теле.
– Это на самом деле интересно! – воскликнул Паша. – Расскажешь, что ты уже узнал?
– Все мы состоим из крошечных клеток, – начал Саша. – Это такие маленькие кирпичики, из которых построено всё наше тело. Они настолько мелкие, что увидеть их можно лишь в микроскоп.
Клетки обладают всеми признаками живого. Они способны размножаться, расти, обмениваться веществами и энергией с окружающей средой, реагировать на изменения, происходящие в этой среде.
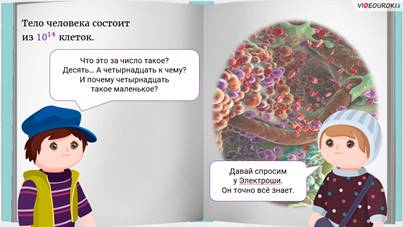
– А сколько клеток в нашем теле? – спросил Паша.
– В энциклопедии я прочитал, что клеток в нашем теле вот такое число 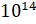
– Давай спросим у Электроши, – предложил Паша. – Он точно всё знает.
– Ребята, прежде чем я вам расскажу о подобных числах, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
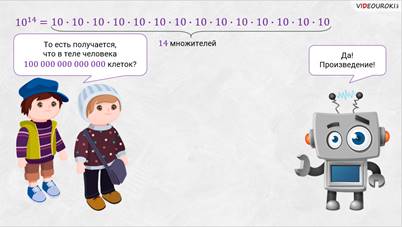
– А теперь вернёмся к вашему вопросу, – продолжил Электроша. – Как вы знаете, сумму нескольких равных слагаемых удобно записывать с помощью произведения. Вот, например, 10 + 10 + 10 + 10 + 10 записывают короче: 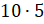
Для произведения, в котором все множители равны, математики тоже придумали способ, с помощью которого такое произведение можно записать короче. Вот вы не могли расшифровать число, обозначающее количество клеток в теле человека. А эта запись обозначает произведение.
– Произведение? – удивились мальчишки.
– Да! Произведение! А точнее говоря, эта запись означает, что нужно 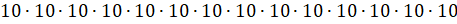
– То есть получается, что в теле человека 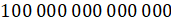
– Получается так! – улыбнулся Электроша. – Кстати, такой способ записи произведения одинаковых множителей придумали давным-давно. Ещё в Древнем Египте учёные обратили внимание на то, что когда нужно выполнить умножение какого-либо числа на себя много раз, то на это тратится огромное количество ненужных усилий. Более того, такая операция ещё и вела к значительным финансовым затратам. Согласно действовавшим тогда установкам на оформление любых записей, каждое действие с числом должно было подробно описываться.
Самый простейший папирус тогда стоил весьма внушительную сумму денег. Вот умным египтянам и пришлось искать выход из сложившейся ситуации. Конечно, впоследствии ещё не один математик внёс усовершенствование в данный способ написания подобного произведения.
– Понятно! Такая запись обозначает произведение. Правильно? – спросили ребята.
– Не просто произведение, а произведение нескольких одинаковых множителей. –––––– Запомните! Выражение 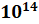
Обратите внимание: в записи степени участвуют два числа. Число, которое возводится в степень, называют основанием степени. В нашем случае это число 10. Другое число называют показателем степени. В нашем случае это 14. Число 14 показывает, сколько множителей, каждый из которых равен десяти, содержит произведение. Само же действие называют возведением в степень.
– Давайте попробуем прочитать следующие выражения: 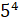
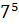
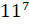
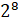
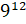
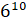
– В первой строчке записаны «пять в четвёртой степени», «семь в пятой степени» и «одиннадцать в седьмой степени», – начал Паша.
– Во второй строчке – «восьмая степень числа два», «двенадцатая степень числа девять» и «десятая степень числа шесть», – продолжил Саша.
– Запомните! – сказал Электроша. – Степенью числа a с натуральным показателем 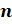
В общем виде степень с основанием a и показателем 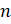
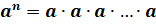
Читают такую запись: «а в степени эн» или «эн-ая степень числа а».
– Электроша, вот ты в определении говоришь, что натуральный показатель больший единицы, – решили уточнить ребята. – А что, показатель степени не может быть равным единице?
– Может, – ответил Электроша, – но это один из особых случаев степени. Давайте порассуждаем. Если показатель степени равен единице, то что это значит?
– Это значит, что основание степени надо взять множителем один раз, – ответили мальчишки.
– Хорошо! Но как это представить? Взяли основание, а второго множителя нет. Так получается?
– Ну да, – задумались мальчишки.
– Поскольку в математике не принято рассматривать произведение, состоящее из одного множителя, то договорились, что 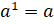
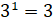
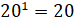
– Электроша, ты сказал, что показатель степени равный единице – это один из особых случаев. А какие ещё есть особые случаи? – спросили ребята.
– Запомните! – начал Электроша. – Любое число в нулевой степени равно единице.
Ноль в любой натуральной степени равен нулю. А вот выражение ноль в нулевой степени считают не имеющим смысла.
Единица в любой степени равна единице.
– А теперь прочитайте вот такие выражения: 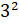
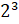
– В первом случае записано «три во второй степени», – начал Паша.
– А во втором – «два в третьей степени», – продолжил Саша.
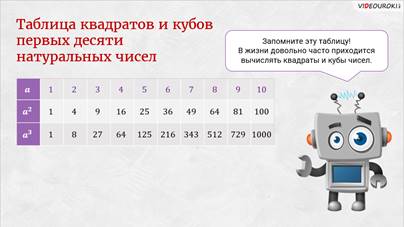
– Молодцы! – похвалил ребят Электроша. – Но часто в жизни вы можете услышать и другие, особые названия второй и третьей степени числа. Вторую степень числа чаще называют квадратом числа. Третью степень числа называют кубом числа. Тогда наше первое выражение можно ещё прочитать как «три в квадрате». А второе можно прочитать как «два в кубе».
На экране вы видите таблицу квадратов и кубов первых десяти натуральных чисел. Запомнив эту таблицу, вы сильно облегчите себе жизнь в будущем. Ведь в жизни довольно часто нам приходится вычислять квадраты и кубы чисел.
– А теперь давайте найдём значение следующего выражения: 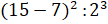
– Электроша, а как выполнять вычисления, когда в выражениях есть степень? – задумались ребята. – Раньше у нас всё было просто: выполняли действия в скобках, потом умножение и деление, если они присутствовали в выражениях, а потом сложение и вычитание.
– Возведение числа в степень – это пятое арифметическое действие, – начал Электроша. Запомните! В выражениях со степенями, не содержащими скобки, сначала выполняют возведение в степень, затем умножение и деление, а в конце сложение и вычитание.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.
– Теперь понятно! – обрадовались мальчишки. – В нашем выражении есть скобки. Значит, первым выполним действие в скобках. У нас вычитание. 15 – 7 = 8. Затем выполним действия со степенями. 8 2 = 64. А 2 3 = 8. Осталось выполнить деление. 64 : 8 = 8.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: возведите в степень:
а) 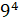
б) 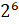
в) 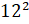
Решение: первое выражение девять в четвёртой степени. Нужно 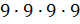
Следующее выражение два в шестой степени. Нужно 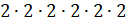
И последнее выражение двенадцать в квадрате. Мы должны 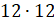
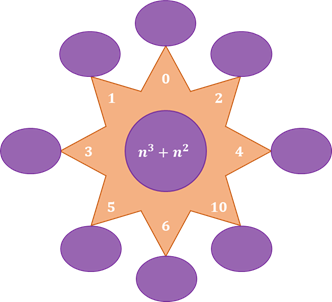
Следующее задание: в каждый из овалов впишите значение выражения 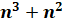
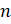
Решение: первое число 0. Подставим его в выражение 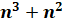
Третье число 4. Подставим его в выражение. 4 3 = 64. 4 2 = 16. Имеем 64 + 16. Получаем 80.
Следующее число 10. 10 3 = 1000. 10 2 = 100. 1000 + 100 = 1100.
Перейдём к следующему числу. 6 3 = 216. 6 2 = 36. 216 + 36 = 252.
Следующее число 5. Подставим его в выражение. Посчитаем. Получим 150.
Перейдём к следующему числу. Подставим его в выражение. Посчитаем. Получим 36.
И последнее число 1. Подставим его в наше выражение. Мы знаем, что единица в любой степени равна единице. Тогда получаем 1 + 1 = 2.
Урок в 5-м классе по теме «Степень числа с натуральным показателем»
Разделы: Математика
Ход урока
1. Все мы любим загадки. Именно с неё мы начнём урок. Отгадайте.
Первый слог возьми из слова “степь”,
Что всегда прекрасною бывает.
Слог второй мы сможем лицезреть,
Если кто в лесу деревья валит. (Сте – пень)
Совершенно верно, вы отгадали. Итак, тема сегодняшнего урока “Степень числа с натуральным показателем”.
Знакомиться с этим важным понятием мы будем вместе с нашей доброй знакомой – Точкой. Она, наверное, где-то отдыхает. Давайте угадаем, где сейчас находится Точка.
Ваша задача составить слово по первым буквам отгадок.
Р – результат вычитания. (разность)
И – то, чем любят заниматься все дети и даже взрослые (игра)
К – то. что есть общее у дерева и у уравнения..(корень)
Ц – то, что мы используем для написания чисел
Действительно, наша точка на представлении в цирке. Представление дают жители Карликании.
1 номер программы – синхронное сложение.
На арене – пятёрки: 5 +5 + 5 + 5
Вопрос: Каким действием можно заменить сложение одинаковых чисел?
– На сцене появились другая пара: 5 · 4. А вместе получилось 5 + 5 + 5 + 5 = 5·4
2 номер программы – магия: восстанови уравнение по его решению.
Давайте поможем нашим артистам из Карликании.
| _ : _ = 5 | |
| х = 25 : 5 | (25 : х = 5) |
| _ : _ = 5 | |
| х = 5 · 5 | (х : 5 = 5) |
3 номер – выходит пятёрка в странной шляпке 5 2
И вдруг на глазах у всех зрителей вместо одной пятёрки появляется выражение: 5·5 и вдруг между артистами установилась связь: 5 2 =5 · 5=25
Вместо этих артистов появились другие: 5 3 =5 · 5 · 5=125
Вдруг послышалась барабанная дробь, на сцене в свете прожекторов появилась пятёрка в новой шляпке 5 100 и через мгновенье на всей арене появилась сотня пятёрок. А между ними – знаки умножения. Зрители ахнули. Как такое могло получиться?
Но невозмутимый ведущий объявил: “С гастролями в Карликании непревзойдённая степень с натуральным показателем”.
Зал взорвался аплодисментами.
Вопрос: Как вы считаете, какое действие можно заменить степенью с натуральным показателем?
– Умножение, причём множители должны быть одинаковые.
Вопрос: Как можно записать произведение пяти двоек?
2 · 2 · 2 · 2 · 2 = 2 5 = 32.
Итак, давайте подведём итог.
Определение. Степенью числа а с натуральным показателем n называют произведение n натуральных множителей, каждый из которых равен а.
а – основание степени, n – показатель степени
А теперь давайте вспомним, как называются степени числа 10.(Дети называют по очереди)
10 4 = 10000 десять тысяч
10 5 = 100000 сто тысяч
10 6 = 1000000 миллион
А вы знаете, кто первый придумал слово миллион?
Великий путешественник Марко Поло.
: Милле по-итальянски – тысяча, конечное – оне, играет у итальянцев ту же роль, что у нас суффикс – ищ. Мильоне, очевидно, тысячища, большая великая тысяча тысяч (удивительного в таком словообразовании мало: наше русское слово тысяча, разъясняют лингвисты, тоже когда-то значило тучная сотня). Так родилось слово миллион, обозначающее число тысяча тысяч. А за первым путешественником, который ознакомил Европу с Азией, закрепилось прозвище “Господин миллион”.
2. Итак. Задача.
Величина обыкновенной комнатной мухи общеизвестна – около 7 мм в длину. Но какова была бы её длина при увеличении в миллион раз? (7000000 мм = 700000 см = 7000 м = 7 км, для сравнения – 7 км это ширина Москвы или Петербурга, т.е. муха, увеличенная линейно в миллион раз могла бы покрыть своим телом столичный город)
Ещё несколько интересных примеров.
Сделав миллион шагов по одному направлению, вы отошли бы километров 600 (например, от Москвы до Петербурга миллион шагов)
Миллион человек, выстроенных в одну шеренгу плечом к плечу, растянулись бы на 250 км.
Зачерпывая миллион раз напёрстком, вы вычерпаете около тонны воды.
Книга в миллион страниц имела бы в толщину метров 50.
Миллион букв заключает книга убористой печати в 600-800 страниц среднего формата.
Миллион дней – более 27 столетий. От начала нашей эры не прошло ещё миллиона дней
Одолела вас дремота,
Шевельнуться неохота?
Ну-ка делайте со мною
Упражнение такое:
Вверх, вниз, потянись.
Окончательно проснись.
Руки вытянуть пошире,
Раз. Два. Три, четыре.
Наклониться – три, четыре
И на месте поскакать.
На носок, потом на пятку.
Все мы делаем зарядку.
А теперь составим таблицу для вычисления степеней числа 2 и 3.