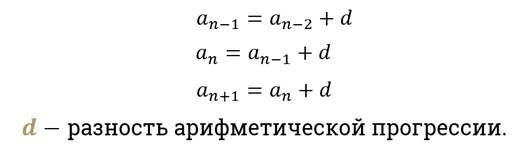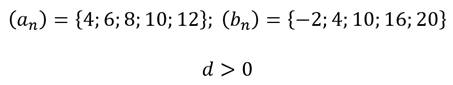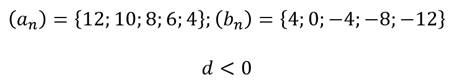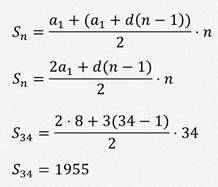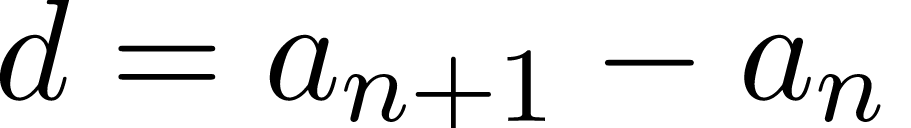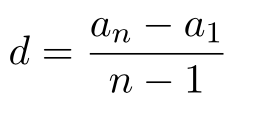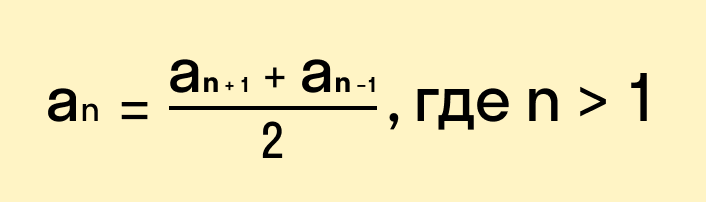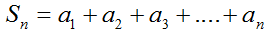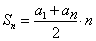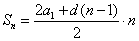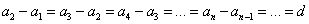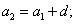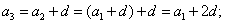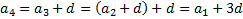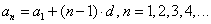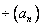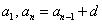в каком классе проходят арифметическую прогрессию

Арифметическая прогрессия

Урок 36. Подготовка к ОГЭ по математике 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Арифметическая прогрессия»

· повторить определение арифметической прогрессии;

· вспомнить свойство арифметической прогрессии;

· вывести формулу для вычисления суммы n первых членов арифметической прогрессии.

Давайте вспомним определение арифметической прогрессии.

Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом.

Это число называется разностью арифметической прогрессии.

Давайте попробуем среди предложенных последовательностей определить, какие являются арифметической прогрессией, а какие нет.

Как и числовые последовательности, арифметические прогрессии бывают возрастающие и убывающие.

Возрастающие – это прогрессии, в которых каждый последующий член больше предыдущего.

Например, примерами возрастающих прогрессий будут прогрессии

Определить возрастающую арифметическую прогрессию нетрудно, достаточно определить разность прогрессии. Если разность арифметической прогрессии больше нуля, то, значит, арифметическая прогрессия возрастающая.

Убывающие арифметические прогрессии – это прогрессии, в которых каждое последующий член меньше предыдущего.

Примерами убывающих прогрессий будут прогрессии

У убывающих арифметических прогрессий – разность арифметической прогрессии меньше нуля.

Рассмотрим ещё один пример.

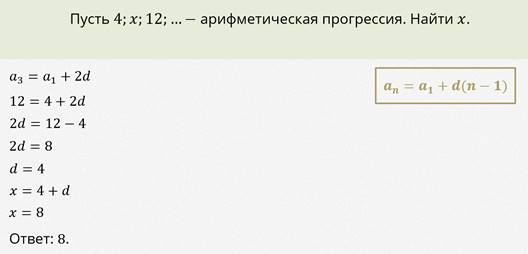
Теперь давайте рассмотрим задачу.

А давайте теперь найдём х, если арифметическая прогрессия такая: 4024; х; 6072?

Вроде тоже ничего сложного, но здесь при вычислении есть шанс сделать вычислительную ошибку.

Давайте решим это задание в общем виде.

Мы с вами сформулировали основное свойство арифметической прогрессии.

Найдём теперь х из предыдущей задачи с помощью только что доказанной формулы.

Теперь давайте выполним задание.

Найти сумму первых девяти членов арифметической прогрессии, состоящей из чётных чисел, записанных в порядке возрастания.

Восстановить девять членов этой последовательности нетрудно.

Это будут числа: 2; 4; 6; 8; 10; 12; 14; 16; 18.

Их сумма равна: 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 = 90.

А если нам надо найти, например, сумму тысячи первых членов? Как быть? Выписывать тысячу членов прогрессии и все их складывать? Это долго и большая вероятность того, что при нахождении всех чисел, мы допустим ошибку, которая повлечёт за собой ошибку при нахождении суммы.

Давайте выведем формулу, которая поможет нам быстро подсчитать сумму сколько угодно членов арифметической прогрессии.

Эта формула, позволяет находить сумму любого количества первых членов арифметической прогрессии, не вычисляя отдельно их значения.

Теперь давайте вернёмся к нашему примеру и посчитаем сумму девяти членов прогрессии по формуле, которую вывели.

Мы получили такой же результат, только нам не пришлось находить все девять членов прогрессии.

Рассмотрим несколько примеров.

Рассмотрим ещё один пример.

Есть второй способ решения такой задачи.

В этом случае, нам не пришлось отдельно вычислять значение тридцать четвёртого члена.

Рассмотрим ещё один пример.

Рассмотрим ещё один пример.

Сегодня на уроке, мы вспомнили определение арифметической прогрессии, повторили свойство арифметической прогрессии, вывели сумму эн первых членов арифметической прогрессии.

Источник

Разработка урока «Арифметическая прогрессия вокруг нас» ( 9 класс).

Ищем педагогов в команду «Инфоурок»

Открытый урок алгебра 9 класс

«Арифметическая прогрессия вокруг нас»

Тип урока: повторительно-обобщающий.

³ Обобщить теоретические знания по теме;

³ Развивать познавательный интерес учащихся, учить их видеть связь между математикой и окружающей жизнью;

развивать грамотную математическую речь;

³ Воспитывать волю и настойчивость для достижения конечных результатов;

Оборудование: мультимедийный проектор, компьютер, раздаточный

дидактический материал для учащихся.

I. Орг.момент, приветствие, пожелания.

Здравствуйте, ребята!. Садитесь, пожалуйста. Сегодняшний урок я хотела бы начать словами А.С. Пушкина: ( слайд 1).

«О, сколько нам открытий чудных….

Готовит просвещенья дух,

Я хочу, чтобы наша встреча сегодня принесла много открытий, опыта и хорошего настроения.

Изучена данная тема,

Пройдена теории схема,
Вы много новых формул узнали,
Задачи с прогрессией решали.

И вот в сегодняшний урок

Вместе с вами мы будем двигаться только вперёд, т.к. слово «Прогрессио» в переводе с греческого языка означает движение вперёд.

1. Итак, ребята, тема нашего сегодняшнего урока ( слайд 2).

Сообщение задач урока.

1.А сейчас мы поработаем устно.

1. В последовательности

назовите первый, третий и шестой члены.

2. Продолжите данную последовательность: 5; 9; 13; 17;…

2.А сейчас в качестве небольшой разминки выполним кроссворд. (слайд 8)

1. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

2. Разность последовательно одинаковых членов.

3. Способ задания последовательности.

4. Разность последующего и предыдущего членов прогрессии.

5. Элементы, из которых состоит последовательность.

6. Натуральное число, обозначающее место члена в последовательности.

7. Функция, заданная на множестве натуральных чисел.

8. Последовательность, содержащая конечное число членов.

Открываем тетради, запишем сегодняшнее число и выполним задание:

Вам предлагается карточка, в которой вы должны «Найти пару», соединив их стрелкой.

1. Какая последовательность называется арифметической прогрессией? Назовите формулу.

2. Как найти разность арифметической прогрессии?. Назовите формулу.

3. Назовите способы задания последовательности.

4. Назовите формулу n – го члена арифметической прогрессии.

5. Сформулируйте свойство каждого члена арифметической прогрессии, начиная со второго. Назовите формулу.

Проверка ответов. (слайд12)

Зная формулы арифметической прогрессии, можно решить много интересных задач литературного, исторического и практического содержания.

Даже в литературе мы встречаемся с математическими понятиями!

Хорей «Я пропАл, как звЕрь в загОне» ( Пастернак)

Итак, арифметическая прогрессия вокруг нас. (слайд15)

1. Проверка умений учащихся применять знания в нетрадиционных ситуациях.

Задача 1: При свободном падении тело проходит в первую секунду 5 м, а в каждую следующую на 10 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 с после начала падения.

(а n ) – арифм.прогрессия

Родители ко Дню рождения своего сына Андрея решили купить и обновить ему мобильный телефон. Для этого они в первый месяц отложили 650 рублей, а в каждый последующий месяц они откладывали на 50 рублей больше, чем в предыдущий. Какая сумма будет у родителей Андрея через 10 месяцев?

Дано:

Ответ:

Прогрессии строителю: Представьте, что вы – учетчик на стройке. Привезли большое количество бревен строевого леса. Нужно быстро определить, сколько бревен привезли, чтобы закрыть наряд шоферу.

Количество бревен легко подчитывается по формуле суммы арифметической прогрессии с разностью, равной единице, если бревна уложены так, как показано на рисунке

Задача 3: При хранении бревен строевого леса их укладывают как показано на рисунке. Сколько брёвен находится в одной кладке, если в ее основании положено 12 бревен?

Курс воздушных ванн начинают с 15 мин. в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1 час 45 минут?

Дано: арифметическая прогрессия, мин, мин,

Найти:

Ответ: 10 дней следует принимать ванны

Задачи из вариантов ОГЭ (слайд 21)

1.Найдите сумму первых двадцати членов арифметической прогрессии (с _n ),если

Закончился двадцатый век.

Куда стремится человек?

Изучен космос и моря,

Строенье звезд и вся земля.

Но математиков зовет

Итак, сегодня мы с вами говорили о прогрессии, которая называется арифметической. Но есть и другая прогрессия. А вот что это за прогрессия, мы узнаем на последующих уроках.

Творческое задание : “Арифметические прогрессии вокруг нас” (задачи, рассказ, эссе, стихотворение, кроссворд и т.д.)

Подобрать «исторические» задачи по теме «Прогрессии».

1.Что вы ожидали от работы на данном уроке? Сравните свои предварительные цели и реально достигнутые результаты.

2. Какие чувства и ощущения возникали у вас в ходе работы? Что оказалось для вас самым неожиданным?

3. Что вам более всего удалось, какие моменты были выполнены наиболее успешно?

4. Перечислите основные трудности, которые вы испытывали во время урока. Как вы их преодолевали?

Я желаю, чтобы арифметические прогрессии и вообще математика вели по жизни вас только вперёд! Я благодарю всех за работу! Мне было приятно с вами общаться! До свидания!

Синквейн. (красивое многоточие)

Пишем синквейн (от англ. «путь мысли»)

Правила написания синквейна:

Одно слово. Существительное или местоимение, обозначающее предмет, о котором идет речь.

Два слова. Прилагательные или причастия, описывающие признаки и свойства выбранного предмета.

Три слова. Глаголы, описывающие совершаемые предметом или объектом действия.

Фраза из четырех слов. Выражает личное отношение автора к предмету или объекту.

Одно слово. Характеризует суть предмета или объекта.

Прогрессия.
Арифметическая, геометрическая.
Складывать, умножать, суммировать.(считать, вычислять)
Широко используется в практической деятельности.
Движение.

4.Разн…сть арифм…тическо… прогресс……

Гимнастика для глаз

Вертикальные движения глаз вверх-вниз.

Вращение глазами по часовой стрелке и против.

Закрыть глаза и представить по очереди цвета радуги как можно отчётливее.

Глазами «нарисовать» кривую, несколько раз, сначала в одном, а затем в другом направлении.

Список использованной литературы, материалов сайтов:

1. Лебединцева Е.А., Беленкова Е.Ю. Алгебра 9 класс. Задачи для обучения и развития учащихся. – М.: Интеллект-Центр, 2006.

2. Макарычев Ю.Н., Миндюк Н.Г. «Алгебра 9 класс», Просвещение, М.: 2010.

3. М.Б. Миндюк, Н. Г. Миндюк, “Разноуровневые дидактические материалы по алгебре. 9 класс”, Издательский дом “Генжер”, 1999г.

4. Энциклопедия для детей. – М., Аванта +, 1997.

5. Лиман М.М. Школьникам о математике и математиках. – М., Просвещение, 1981.

Понятие арифметическая прогрессия. Формула n – члена арифметической прогрессии:

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Международная дистанционная олимпиада Осень 2021

Похожие материалы

Презентация по алгебре «Геометрическая прогрессия»

Презентация по алгебре «Арифметическая прогрессия»

Конспект урока по математике по теме «Простые и составные числа»

Урок- игра по алгебре в 7 классе по теме «Формулы сокращенного умножения»

Интегрированный урок по математике и истории в 8 классе по теме «Битва под Москвой»

Разработка внеклассного мероприятия по математике «Математическое кафе» (10-11 классы)

Конспект урока по алгебре для 8 класса по теме «Еще одна формула корней квадратного уравнения»

Презентация по алгебре на тему » Неполные квадратные уравнения»

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5267714 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Прослушивание музыки снижает усталость мозга

Время чтения: 1 минута

Роспотребнадзор продлил действие санитарных правил для школ

Время чтения: 1 минута

Жириновский предложил ввести в школах уроки полового воспитания

Время чтения: 1 минута

Рособрнадзор открыл горячую линию по вопросам контрольных в школах

Время чтения: 1 минута

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

В Приамурье начнут пускать на занятия только привитых студентов

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Арифметическая прогрессия свойства и формулы

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

«Последовательность простых чисел: 4, 6, 10, 19, 21, 33. »

Последовательность y_n = C называют постоянной или стационарной.

Арифметическая прогрессия — (a_n), задана таким соотношением:
a₁ = a, a_n+1= a_n + d.

Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a_n+1 = a_n + a_n-1.

Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

Свойства числовых последовательностей:

Возрастающие и убывающие последовательности называют монотонными последовательностями.

Пример числовой последовательности выглядит так:

В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

N-ный член алгебраической последовательности — это число с порядковым номером n.

Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a₁, a₂. a₁₀. a_n.

N-ый член последовательности можно задать формулой. Например:

Определение арифметической прогрессии

Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.

Рассмотрим основные определения и как найти арифметическую прогрессию.