в каком классе начинают учить дроби
Урок математики в 4-м классе по теме: «Дроби»
формирование знаний, умений, навыков действий с дробями;
развитие памяти логического мышления, воображения, внимания, речи, математических навыков вычисления;
воспитание чувства ответственности, коллективизма, взаимопомощи, аккуратности, самостоятельности, дисциплины, наблюдательности.
Оборудование: модели долей демонстрационная и раздаточная, заготовка-круг, танграмм, схемы задач, таблицы с дробями.
I. Организационный момент.
II. Сообщение темы урока.
– Тема нашего урока. Вот беда. Пропала тема. Никто не видел? Придется вам ее восстановить. Давайте решим примеры, и ответы запишем в порядке возрастания.
Расположить примеры в порядке возрастания ответов и прочесть получившееся слово.
О 12000 : 4000 х 7 х 10 = (210);
Б 720 : 90 x 10 x 8 = (640);
И 90 x 30 : 100 x 1000 = (27000);
На доске появляется название темы: «Дроби».
IV. Постановка цели урока
Сценка “ Буратино на уроке у Мальвины.”
– А сейчас Буратино мы займемся арифметикой.
– Вот вам яблоко (дает). Представьте, что к вам подошел Некто просит поделиться яблоком. Сколько достанется каждому?
– Нисколько! Я не дам Некто яблока, хоть он со мной дерись!
– Буратино, подумайте внимательно. Вам не надо отдавать яблоко, вам надо его поделить. (Буратино думает.)
– Никак не делится. Вот если бы у меня было 2 яблока, то может быть и можно было бы поделить, и то вряд ли, а одно, ну ни как не делится.
– Нет в арифметике такого действия, чтобы одно яблоко на двоих делить.
– Буратино, у вас нет никаких способностей к арифметике. Придется вас отправить в 4 “А” класс. У них как раз это изучают.
– Что, ребята, поможем Буратино?
V. Формирование знаний, умений и навыков.
Нам часто в жизни приходится делить целое на части. Представьте, что к вам пришли гости, а у вас 1 торт. Как быть? Надо делить его поровну. Возьмите на столе модель “торта” (круг).
Учитель показывает, дети повторяют.
К I-у варианту пришло 3 гостя + хозяин. Делим на 4 части. А ко II-у варианту пришло 7 гостей + хозяин. Делим на 8 частей. Разрезаем по линии сгиба на части. Доли получили, а как это записать? С помощью, каких таких знаков? Для звуков мы используем буквы, для записи чисел – цифры, а как записать доли? Доли мы запишем с помощью дробей.
Дробь – это одна или несколько равных долей, записанных с помощью двух натуральных чисел, разделенных чертой
, где – m числитель, а n – знаменатель.
Вывешивается запись на доске, а дети записывают в тетрадь.
– Теперь давайте запишем дроби.
– На сколько частей делили? Записываем под чертой.
– Сколько таких частей взяли? Пишем над чертой.
– На сколько равных частей поделена фигура?
– Сколько частей закрашено?
– Сколько частей незакрашено?
– Как записать с помощью дроби?
3) Закрашивание дробей.
– На сколько частей поделена фигура?
– Сколько надо закрасить?
– Что вам об этом говорит? (Числитель и знаменатель)
– На что указывает числитель дроби? (Сколько частей взято.)
– На что указывает знаменатель дроби? (На сколько частей поделили.)
5) Запись дробей с помощью знака «% «. Запись % с помощью дробей.
6) Сравнение дробей.
1 вариант: возьмите 1/4 часть;
2 вариант: возьмите 1/8 часть;
– У кого больше? Что мы видим?
Дети сравнивают в парах способом наложения. Учитель на модели
Вывод: чем больше знаменатель, при одинаковом числителе, тем меньше дробь, чем меньше знаменатель, при одинаковом числителе, тем больше дробь.
VI. Соревнование по рядам у доски.
Таблицы с дробями вывешиваются на доску. Детям предлагается только поставить знак между парой дробей.
| 1/7 1/10; 1/100 > 1/1000; | 1/4 > 1/5; 1/9 > 1/13; 1/17 2/9; 7/16 > 3/16; 9/2 1 5/40. |
Таблицы с дробями вывешиваются на доску. Детям предлагается только поставить знак между парой дробей.
7) Сложение и вычитание дробей.
Вывод: при одинаковых знаменателях дроби складывают и вычитают как натуральные числа.
Таблицы с дробями вывешиваются на доску. Детям предлагается только записать ответ. От каждого ряда выходят ученики по очереди и записывают ответы. Проверка.
1/8 + 1/4
6/9 + 1/9
7/10 + 3/10
5/15 + 10/15
– Что известно?
– Что надо найти?
– Как найти?
VIII. Самостоятельная работа по рядам.
– Что нового узнали?
– Что такое дробь?
– Какая дробь больше?
– Как складывают и вычитают дроби?
– Сегодня получили оценки 20/4 и 20/5.
Х. Дополнительный материал. Танграмм.
– Определите сколько частей каждого цвета на рисунке и составьте свой рисунок.
Детям раздаются карточки, где изображён с помощью 8 разноцветных треугольников рисунок, и даны отдельно ещё 8 разноцветных треугольников, что бы дети сами составили свой рисунок.
“ Пришел из школы ученик
И папе с мамой говорит:
“Задачку задали у нас,
Ее решал я целый час.
И вышло у меня в ответе
Два землекопа и две трети!”
Дроби и доли.
Дроби самая сложная тема для учеников начальных классов. Но даже самая трудная тема может стать простой и понятной. Для обучения детей нужно использовать фантазию и элементы игры. А главное – сохранять спокойствие.
В серьезных учебниках по математике есть знаки: и сложение, и вычитание, и умножение. А вот, привычного нам, с вами знака деления (:) – нет. Получается, что знаком деления (:) пользуются только ученики начальной школы? На самом деле – нет. Только этот знак можно писать и по-другому, вот такой чертой, она пишется посередине клетки:
Вот это все – деление.
Деление можно записывать не двумя точками, а горизонтальной полоской.
Так вот: любая математическая запись, в которой присутствует знак деления в виде черточки, называется дробью.
Слово «дробь» говорит само за себя – оно обозначает дробление или деление.
Для записи дробей используются цифры и черта, которую называют дробной.
Вы когда-нибудь видели военный парад? Идут солдаты стройными рядами, а впереди человек со знаменем (флагом) – знаменосец! И по знамени легко понять, к какому роду войск принадлежат эти солдаты. У дроби тоже есть «знаменосец» — это главное число, которое обозначает, на сколько равных частей разделили целое (предмет, фигуру или величину).
«Знаменосец» пишется под дробной чертой и называется ЗНАМЕНАТЕЛЬ.
А число, над чертой показывает, сколько таких частей взяли (или закрасили, или съели). Это число называют ЧИСЛИТЕЛЕМ.
читается – две третьих, можно заменить по-другому — 2 : 3.
Рассмотрим еще одно число: раньше мы не могли на уроке математики 1 разделить на 2. А теперь – умеем: 1 разделить на 2 – это не что иное, как одна вторая. Что же это значит? Если в математике мы с вами не делали этого ни разу, то в жизни вы это делаем постоянно. Предположим, у вас есть яблоко. И вам нужно разделить его между вами и другом. Т.е. одно яблоко разделить на 2.
Так что же за число такое – одна вторая, во-первых, это дробь потому что присутствует знак деления, во-вторых, оно меньше единицы.
Потому что нельзя один разделить на 2, чтобы получилось что-то больше 1.
В-третьих, оно обозначает, что мы целое разделили на 2 и взяли себе одну такую часть.
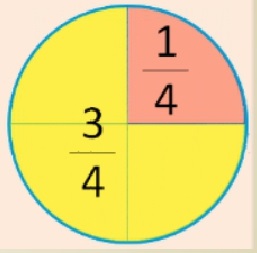
Давайте посмотрим на число:
По правилу, которое мы с вами вывели: три четвертых – это тоже самое, что три разделить на 4.
Давайте посмотрим, как это понять. Круг разделим на 4 равные части.
3 части закрасим желтым цветом. Это и есть три четвертых. Что же это значит?
Во-первых, это тоже дробь.
Во-вторых, она тоже меньше единицы.
И она обозначает, что круг мы разделили на 4 части
и закрасили желтым цветом – 3 таких части.
Итак,
как вы уже поняли: любая дробь будет иметь черту.
Ее так и называют – дробная черта. И обязательно будет стоять какое-то число над чертой и какое-то число под чертой.
Давайте научимся, как правильно читать дроби.
Читают их так: верхнее число всегда будет отвечать на вопрос: сколько?, а нижнее будет отвечать на вопрос: какая? или каких?
Сколько? – три, каких? – восьмых – три восьмых,
Сколько? – семь, каких? – девятых – семь девятых,
Сколько? – две, каких? – шестых – две шестых,
Сколько? – пять, каких? – седьмых – пять седьмых.
У чисел, которые вверху и внизу дроби есть свое научное название: верхнее число называется числитель, а нижнее – знаменатель.
Постарайтесь запомнить это. Это важно! Числитель – наверху, знаменатель – внизу.
Знаменатель показывает на сколько частей мы разделили наше целое, а числитель показывает – сколько частей целого мы с вами взяли.
Чтобы лучше запомнить, где числитель, где знаменатель, есть простая напоминалочка:
«ЧЕЛОВЕК ХОДИТ ПО ЗЕМЛЕ».
Ч – числитель – «над», З – знаменатель «под».
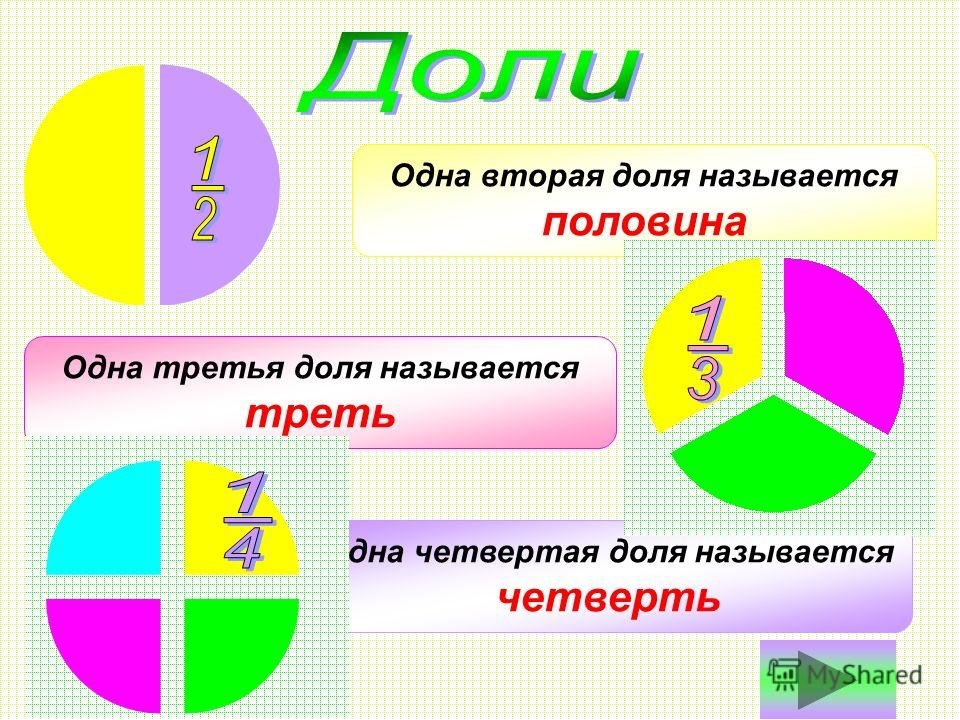
Есть одна разновидность дробей, которую в начальной школе выделяют в отдельную группу. Такие дроби называют долями. Если вам встретилось слово «доля», знайте, что это та же самая дробь, но только у нее числитель равен единице.
Мы постоянно сталкиваемся с ними в жизни.
Чаще всего мы встречаемся в жизни именно с половиной:
пол яблока — это одна вторая яблока, пол стакана – это одна вторая стакана.
Так же мы знакомы с одной третьей:
– это не что иное, как треть.
Треть грейфрута – это значит, разделили грейфрут на 3 части и взяли одну.
Точно так же мы с вами называем одну четвертую четвертью.
Например – школьная четверть. Мы с вами делим учебный год на 4 части и берем одну часть. Это и есть – четверть.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.9 / 5. Количество оценок: 78
Когда дети начинают изучать дроби в школе?
Моя дочь, 9 лет, начинает подвергаться дроблению в школе. Я пытался помочь ей с основной арифметикой дроби, но, похоже, не захожу слишком далеко. Я говорил с ее учителем, который в основном сказал мне не вмешиваться, ее учитель такой. В остальном моя дочь очень умная, поэтому я слишком настаиваю в ее возрасте, чтобы она могла делать такие вещи, как 2/3 x 3/7?
Я не думаю, что вы настаиваете на этом слишком сильно. Если учитель сказал «не вмешивайся», я бы попытался обсудить это с кем-то более высоким. Я, например, приветствую родителей, которые участвуют в академической жизни своих детей. Моему племяннику 9 лет, и он делает дроби, он даже пришел ко мне примерно за шесть или семь недель до того, как его учитель впервые затронул тему в классе, и я заставил его делать основные дроби, прежде чем класс когда-либо узнал о / 2.
Конечно, заставить ее понять две трети из трех седьмых может быть немного сложно, но опять же, я говорю это только потому, что знаю очень многих взрослых, которые этого не понимают.
Как учитель четвертого класса, позвольте мне, надеюсь, пролить некоторый свет на то, что здесь кажется двумя разными вопросами: как учитель вашего ребенка советовал вам, и имеет ли значение продвижение знаний по доле вашего ребенка или нет.
Отвечая на первый вопрос, если этот учитель на самом деле сказал «не вмешивайся» без дальнейших объяснений, то этот учитель должен немного освоиться. Позвольте мне попытаться перефразировать то, что, возможно, подразумевалось; часто я предлагаю родителям отойти от домашней работы из-за двух вещей: если задание возвращается полным и правильным, но родитель должен был провести своего ребенка через весь процесс, тогда я не получаю точного прочтения информации о ребенке. понимание темы. Если у меня нет точного прочтения, я не могу знать, уделить ли им дополнительное внимание, потому что я предполагаю, что они это понимают. Помощь в выполнении домашних заданий всегда велика, но я предпочитаю, чтобы родители задавали своим детям вопросы о том, как они научились этому в школе, и старались максимально подробно объяснить процесс, прежде чем к ним присоединятся родители.
Вторая причина, по которой мы говорим «не беспокойтесь о домашней работе», заключается в том, что мы уважаем вашу домашнюю жизнь и не хотим, чтобы вы испытывали дополнительное напряжение, борясь за тупой рабочий лист ночью, когда все устали. Мы пытаемся быть на вашей стороне.
надеюсь, это поможет
Во-первых, вы должны настаивать, чтобы получить лучшее образование для вашего ребенка. Великие учителя с лучшими намерениями не всегда знают, что лучше.
Во-вторых, вы можете просто попробовать разные подходы к обучению дроби. Я не знаю точно, как вы проходите через них со своей дочерью, но если она продвинута или одарена во всем остальном, то это не должно быть трудным. Вы расстроены и, возможно, это расстраивает вашу дочь? Вы пробовали другую книгу по математике или рабочую тетрадь?
Я учу своих детей по математике дома, так как здесь я не доверяю современным методам, и поскольку математика была для меня сильным предметом, я доверяю тому, что знаю.
Я думаю, что 9 уходит поздно. Нашей дочери 6 лет, она знает, что такое яблоко и что такое половина яблока, и что такое четверть в нескольких играх. Она экстраполировала, что если четверть 4 равна 1, то четверть 8 должна быть 2, а затем она ответила, что четверть 6 = 1 и две четверти. Затем она хотела бороться со своим братом, поэтому мы остановились, но дети получают это рано, если это актуально.
В нашей детской школе большое количество детей с особыми потребностями, поэтому дети на другом конце не получают приоритета, поэтому мне кажется, что вмешательство родителей важно, чтобы эти дети легко справлялись с этой задачей.
Если у нее проблемы, я бы посмотрел, есть ли другой способ объяснить это. Попробуйте использовать фрукты; нарежьте яблоко на 4 (или 6 или 8) кусочка, затем дайте ребенку один кусочек. Объясните, что кусок, который у них есть, является одним из восьми частей, составляющих целое яблоко, и поэтому он составляет одну восьмую или 1/8. Тогда дайте им еще один кусок. Теперь у них есть две фигуры из восьми, или 2/8. Я не уверен, что им нужно знать о наименьших сроках, но если они это сделают, соедините пары частей вместе и покажите, что их две части плюс пары остальных шести могут образовывать четыре части целого, который у них один, поэтому их две восьмые также равны четверти яблока. Часто дети не получают цифры, потому что они не видят, что представляют цифры. Если выразить это с точки зрения чего-то реального,
Прохождение программы курса математики 5–6-х классов за 1,5 учебных года
Разделы: Математика
Математическое образование в нашей стране получают все школьники, начиная с первого года обучения и до последнего. Само собой разумеется, что лишь небольшая часть обучающихся впоследствии станет сама развивать математику. Но применять математические знания и методы станут все. Очень важно, чтобы учащиеся видели прикладные возможности всех разделов математики и почувствовали значение строгих логических рассуждений для всех видов деятельности.
Как же строится школьный курс математики?
В курсе математики для V-XI кл. с учётом возрастных особенностей выделяются три ступени обучения: V-VI, VII-IX, X-XI классы.
В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, с положительными и отрицательными числами, знакомятся с буквенными выражениями, учатся составлять по условию текстовой задачи несложные линейные уравнения и решать их.
Следует отметить, что в V классе слишком много времени уделяется (по стандартной программе) повторению изученного в начальной школе.
Чтобы преодолеть такое положение вещей, делаются различные попытки, одной из которых является разработанная Г.Г. Левитасом переходная программа. Она рассчитана на изучение курса V-VI классов за один учебный год при пяти часах математики в неделю. Изучение этой программы предложено вести по учебникам Н.Я. Виленкина. При этом в течении каждой четверти программа строится из расчёта один пятиурочный цикл в неделю.
Нами было разработано планирование, рассчитанное на изучение математики в V кл. при четырёх часах в неделю, а в VI кл. при пяти часах в неделю. В пятом классе пятый час в неделю может быть использован учителем на свое усмотрение. В зависимости от уровня математической подготовки учащихся, им могут быть предложены задания развивающего характера или задания на ликвидацию пробелов по изучаемой теме. Программа рассчитана на изучение материала V-VI классов за 1,5 учебных года, и поэтому в VI классе со II полугодия необходимо приступать к изучению материала VII класса.
В рамках V класса изучаются следующие темы: натуральные числа (повторение изученного в начальной школе), обыкновенные и десятичные дроби.
В VI классе: отрицательные и положительные числа, пропорции и проценты, решение уравнений и координатная плоскость.
5 КЛАСС
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА ПО КУРСУ «МАТЕМАТИКА» В 5-КЛАССЕ (ПО ЧЕТВЕРТЯМ).
I четверть 9*4 ч.=З6 ч.
| № уроков | Содержание | Кол-во уроков |
| 1-12 | Действия с натуральными числами. | 12 |
| 13-16 | Свойства действий с натуральными числами. | 4 |
| 17-20 | Решение уравнений. | 4 |
| 21-30 | Решение задач (типа «во ск.», «на ск.», больше-меньше; «на», «в», на движение). | 10 |
| 31 | Подготовка к контрольной работе. | 1 |
| 32 | Контрольная работа №1 | 1 |
| 33-36 | Десятичная система исчисления, меры длины. | 4 |
II четверть 7*4 ч.=28 ч.
| № уроков | Содержание | Кол-во уроков |
| 36-39 | Что такое десятичная дробь. Сравнение десятичных дробей. | 4 |
| 40-43 | Сложение и вычитание десятичных дробей. | 4 |
| 44-46 | Решение уравнений. | 3 |
| 47 | Подготовка к контрольной работе. | 1 |
| 48 | Контрольная работа № 2. | 1 |
| 49-52 | Умножение десятичных дробей. | 4 |
| 53-56 | Деление десятичных дробей. | 4 |
| 57-59 | Решение уравнений. | 3 |
| 60 | Подготовка к контрольной работе. | 1 |
| 61 | Контрольная работа № 3. | 1 |
| 62-63 | Округление десятичных дробей. Прикидка | 2 |
III четверть 10*4 ч.=40 ч.
| № уроков | Содержание | Кол-во уроков |
| 64-66 | Обыкновенная дробь. Сравнение на луче. | 3 |
| 67-68 | Правильные и неправильные дроби. Сравнение с 1. | 2 |
| 69-72 | Признаки делимости. Разложение на простые множители. НОД. | 4 |
| 73-76 | Основное свойство. Сокращение дробей. | 4 |
| 77-80 | Сложение, вычитание и сравнение дробей с одинаковыми знаменателями. | 4 |
| 81 | Подготовка к контрольной работе. | 1 |
| 82 | Контрольная работа №4. | 1 |
| 83-86 | НОК. Приведение к общему знаменателю. | 4 |
| 87-90 | Сравнение, сложение и вычитание дробей с разными знаменателями. | 4 |
| 91-93 | Решение уравнений. | 3 |
| 94 | Подготовка к контрольной работе. | 1 |
| 95 | Контрольная работа №5. | 1 |
| 96-99 | Умножение обыкновенных дробей. | 4 |
| 100-104 | Деление обыкновенных дробей. | 4 |
IV четверть 8*4 ч.=32ч.
| № уроков | Содержание | Кол-во уроков |
| 105-107 | Решение уравнений. | 3 |
| 108 | Подготовка к контрольной работе. | 1 |
| 109 | Контрольная работа №6. | 1 |
| 110-113 | Смешанные числа. | 4 |
| 114-117 | Три задачи на дроби. | 4 |
| 118-121 | Решение текстовых задач (составление уравнений, проценты). | 4 |
| 122 | Подготовка к контрольной работе. | 1 |
| 123 | Контрольная работа №7. | 1 |
| 124-127 | Все действия обыкновенными и десятичными дробями. | 4 |
| 128-134 | Повторение. Итоговая контрольная работа. | 7 |
6 КЛАСС
Из программы 6 класса осталось пройти следующие темы: «Положительные и отрицательные числа», «Решение уравнений», «Координатная плоскость», «Пропорция».
За I четверть изучаются положительные и отрицательные числа, координатная плоскость. Первые уроки четверти посвящаются повторению пройденного в 5 классе.
II четверть начинается с изучения темы: «Решение уравнений», а затем до конца четверти учащиеся занимаются нахождением неизвестного члена пропорции и решают задачи на прямую и обратную пропорциональную зависимость.
С окончанием II четверти заканчивается изучение материала 6-го класса.
 , где – m числитель, а n – знаменатель.
, где – m числитель, а n – знаменатель.