в каком классе изучаются дроби
Дроби и доли.
Дроби самая сложная тема для учеников начальных классов. Но даже самая трудная тема может стать простой и понятной. Для обучения детей нужно использовать фантазию и элементы игры. А главное – сохранять спокойствие.
В серьезных учебниках по математике есть знаки: и сложение, и вычитание, и умножение. А вот, привычного нам, с вами знака деления (:) – нет. Получается, что знаком деления (:) пользуются только ученики начальной школы? На самом деле – нет. Только этот знак можно писать и по-другому, вот такой чертой, она пишется посередине клетки:
Вот это все – деление.
Деление можно записывать не двумя точками, а горизонтальной полоской.
Так вот: любая математическая запись, в которой присутствует знак деления в виде черточки, называется дробью.
Слово «дробь» говорит само за себя – оно обозначает дробление или деление.
Для записи дробей используются цифры и черта, которую называют дробной.
Вы когда-нибудь видели военный парад? Идут солдаты стройными рядами, а впереди человек со знаменем (флагом) – знаменосец! И по знамени легко понять, к какому роду войск принадлежат эти солдаты. У дроби тоже есть «знаменосец» — это главное число, которое обозначает, на сколько равных частей разделили целое (предмет, фигуру или величину).
«Знаменосец» пишется под дробной чертой и называется ЗНАМЕНАТЕЛЬ.
А число, над чертой показывает, сколько таких частей взяли (или закрасили, или съели). Это число называют ЧИСЛИТЕЛЕМ.
читается – две третьих, можно заменить по-другому — 2 : 3.
Рассмотрим еще одно число: раньше мы не могли на уроке математики 1 разделить на 2. А теперь – умеем: 1 разделить на 2 – это не что иное, как одна вторая. Что же это значит? Если в математике мы с вами не делали этого ни разу, то в жизни вы это делаем постоянно. Предположим, у вас есть яблоко. И вам нужно разделить его между вами и другом. Т.е. одно яблоко разделить на 2.
Так что же за число такое – одна вторая, во-первых, это дробь потому что присутствует знак деления, во-вторых, оно меньше единицы.
Потому что нельзя один разделить на 2, чтобы получилось что-то больше 1.
В-третьих, оно обозначает, что мы целое разделили на 2 и взяли себе одну такую часть.
Давайте посмотрим на число:
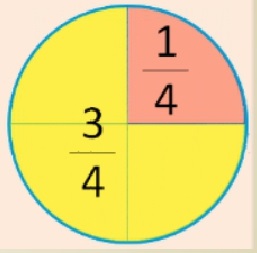
По правилу, которое мы с вами вывели: три четвертых – это тоже самое, что три разделить на 4.
Давайте посмотрим, как это понять. Круг разделим на 4 равные части.
3 части закрасим желтым цветом. Это и есть три четвертых. Что же это значит?
Во-первых, это тоже дробь.
Во-вторых, она тоже меньше единицы.
И она обозначает, что круг мы разделили на 4 части
и закрасили желтым цветом – 3 таких части.
Итак,
как вы уже поняли: любая дробь будет иметь черту.
Ее так и называют – дробная черта. И обязательно будет стоять какое-то число над чертой и какое-то число под чертой.
Давайте научимся, как правильно читать дроби.
Читают их так: верхнее число всегда будет отвечать на вопрос: сколько?, а нижнее будет отвечать на вопрос: какая? или каких?
Сколько? – три, каких? – восьмых – три восьмых,
Сколько? – семь, каких? – девятых – семь девятых,
Сколько? – две, каких? – шестых – две шестых,
Сколько? – пять, каких? – седьмых – пять седьмых.
У чисел, которые вверху и внизу дроби есть свое научное название: верхнее число называется числитель, а нижнее – знаменатель.
Постарайтесь запомнить это. Это важно! Числитель – наверху, знаменатель – внизу.
Знаменатель показывает на сколько частей мы разделили наше целое, а числитель показывает – сколько частей целого мы с вами взяли.
Чтобы лучше запомнить, где числитель, где знаменатель, есть простая напоминалочка:
«ЧЕЛОВЕК ХОДИТ ПО ЗЕМЛЕ».
Ч – числитель – «над», З – знаменатель «под».
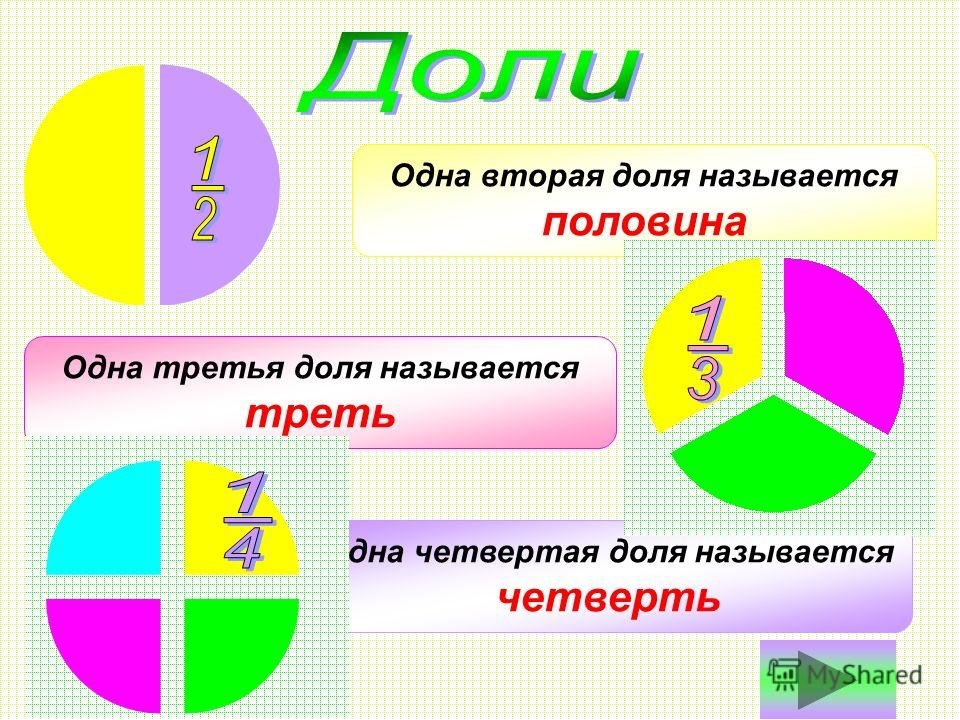
Есть одна разновидность дробей, которую в начальной школе выделяют в отдельную группу. Такие дроби называют долями. Если вам встретилось слово «доля», знайте, что это та же самая дробь, но только у нее числитель равен единице.
Мы постоянно сталкиваемся с ними в жизни.
Чаще всего мы встречаемся в жизни именно с половиной:
пол яблока — это одна вторая яблока, пол стакана – это одна вторая стакана.
Так же мы знакомы с одной третьей:
– это не что иное, как треть.
Треть грейфрута – это значит, разделили грейфрут на 3 части и взяли одну.
Точно так же мы с вами называем одну четвертую четвертью.
Например – школьная четверть. Мы с вами делим учебный год на 4 части и берем одну часть. Это и есть – четверть.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.9 / 5. Количество оценок: 78
Урок математики в 4-м классе по теме: «Дроби»
формирование знаний, умений, навыков действий с дробями;
развитие памяти логического мышления, воображения, внимания, речи, математических навыков вычисления;
воспитание чувства ответственности, коллективизма, взаимопомощи, аккуратности, самостоятельности, дисциплины, наблюдательности.
Оборудование: модели долей демонстрационная и раздаточная, заготовка-круг, танграмм, схемы задач, таблицы с дробями.
I. Организационный момент.
II. Сообщение темы урока.
– Тема нашего урока. Вот беда. Пропала тема. Никто не видел? Придется вам ее восстановить. Давайте решим примеры, и ответы запишем в порядке возрастания.
Расположить примеры в порядке возрастания ответов и прочесть получившееся слово.
О 12000 : 4000 х 7 х 10 = (210);
Б 720 : 90 x 10 x 8 = (640);
И 90 x 30 : 100 x 1000 = (27000);
На доске появляется название темы: «Дроби».
IV. Постановка цели урока
Сценка “ Буратино на уроке у Мальвины.”
– А сейчас Буратино мы займемся арифметикой.
– Вот вам яблоко (дает). Представьте, что к вам подошел Некто просит поделиться яблоком. Сколько достанется каждому?
– Нисколько! Я не дам Некто яблока, хоть он со мной дерись!
– Буратино, подумайте внимательно. Вам не надо отдавать яблоко, вам надо его поделить. (Буратино думает.)
– Никак не делится. Вот если бы у меня было 2 яблока, то может быть и можно было бы поделить, и то вряд ли, а одно, ну ни как не делится.
– Нет в арифметике такого действия, чтобы одно яблоко на двоих делить.
– Буратино, у вас нет никаких способностей к арифметике. Придется вас отправить в 4 “А” класс. У них как раз это изучают.
– Что, ребята, поможем Буратино?
V. Формирование знаний, умений и навыков.
Нам часто в жизни приходится делить целое на части. Представьте, что к вам пришли гости, а у вас 1 торт. Как быть? Надо делить его поровну. Возьмите на столе модель “торта” (круг).
Учитель показывает, дети повторяют.
К I-у варианту пришло 3 гостя + хозяин. Делим на 4 части. А ко II-у варианту пришло 7 гостей + хозяин. Делим на 8 частей. Разрезаем по линии сгиба на части. Доли получили, а как это записать? С помощью, каких таких знаков? Для звуков мы используем буквы, для записи чисел – цифры, а как записать доли? Доли мы запишем с помощью дробей.
Дробь – это одна или несколько равных долей, записанных с помощью двух натуральных чисел, разделенных чертой
, где – m числитель, а n – знаменатель.
Вывешивается запись на доске, а дети записывают в тетрадь.
– Теперь давайте запишем дроби.
– На сколько частей делили? Записываем под чертой.
– Сколько таких частей взяли? Пишем над чертой.
– На сколько равных частей поделена фигура?
– Сколько частей закрашено?
– Сколько частей незакрашено?
– Как записать с помощью дроби?
3) Закрашивание дробей.
– На сколько частей поделена фигура?
– Сколько надо закрасить?
– Что вам об этом говорит? (Числитель и знаменатель)
– На что указывает числитель дроби? (Сколько частей взято.)
– На что указывает знаменатель дроби? (На сколько частей поделили.)
5) Запись дробей с помощью знака «% «. Запись % с помощью дробей.
6) Сравнение дробей.
1 вариант: возьмите 1/4 часть;
2 вариант: возьмите 1/8 часть;
– У кого больше? Что мы видим?
Дети сравнивают в парах способом наложения. Учитель на модели
Вывод: чем больше знаменатель, при одинаковом числителе, тем меньше дробь, чем меньше знаменатель, при одинаковом числителе, тем больше дробь.
VI. Соревнование по рядам у доски.
Таблицы с дробями вывешиваются на доску. Детям предлагается только поставить знак между парой дробей.
| 1/7 1/10; 1/100 > 1/1000; | 1/4 > 1/5; 1/9 > 1/13; 1/17 2/9; 7/16 > 3/16; 9/2 1 5/40. |
Таблицы с дробями вывешиваются на доску. Детям предлагается только поставить знак между парой дробей.
7) Сложение и вычитание дробей.
Вывод: при одинаковых знаменателях дроби складывают и вычитают как натуральные числа.
Таблицы с дробями вывешиваются на доску. Детям предлагается только записать ответ. От каждого ряда выходят ученики по очереди и записывают ответы. Проверка.
1/8 + 1/4
6/9 + 1/9
7/10 + 3/10
5/15 + 10/15
– Что известно?
– Что надо найти?
– Как найти?
VIII. Самостоятельная работа по рядам.
– Что нового узнали?
– Что такое дробь?
– Какая дробь больше?
– Как складывают и вычитают дроби?
– Сегодня получили оценки 20/4 и 20/5.
Х. Дополнительный материал. Танграмм.
– Определите сколько частей каждого цвета на рисунке и составьте свой рисунок.
Детям раздаются карточки, где изображён с помощью 8 разноцветных треугольников рисунок, и даны отдельно ещё 8 разноцветных треугольников, что бы дети сами составили свой рисунок.
“ Пришел из школы ученик
И папе с мамой говорит:
“Задачку задали у нас,
Ее решал я целый час.
И вышло у меня в ответе
Два землекопа и две трети!”
Прохождение программы курса математики 5–6-х классов за 1,5 учебных года
Разделы: Математика
Математическое образование в нашей стране получают все школьники, начиная с первого года обучения и до последнего. Само собой разумеется, что лишь небольшая часть обучающихся впоследствии станет сама развивать математику. Но применять математические знания и методы станут все. Очень важно, чтобы учащиеся видели прикладные возможности всех разделов математики и почувствовали значение строгих логических рассуждений для всех видов деятельности.
Как же строится школьный курс математики?
В курсе математики для V-XI кл. с учётом возрастных особенностей выделяются три ступени обучения: V-VI, VII-IX, X-XI классы.
В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, с положительными и отрицательными числами, знакомятся с буквенными выражениями, учатся составлять по условию текстовой задачи несложные линейные уравнения и решать их.
Следует отметить, что в V классе слишком много времени уделяется (по стандартной программе) повторению изученного в начальной школе.
Чтобы преодолеть такое положение вещей, делаются различные попытки, одной из которых является разработанная Г.Г. Левитасом переходная программа. Она рассчитана на изучение курса V-VI классов за один учебный год при пяти часах математики в неделю. Изучение этой программы предложено вести по учебникам Н.Я. Виленкина. При этом в течении каждой четверти программа строится из расчёта один пятиурочный цикл в неделю.
Нами было разработано планирование, рассчитанное на изучение математики в V кл. при четырёх часах в неделю, а в VI кл. при пяти часах в неделю. В пятом классе пятый час в неделю может быть использован учителем на свое усмотрение. В зависимости от уровня математической подготовки учащихся, им могут быть предложены задания развивающего характера или задания на ликвидацию пробелов по изучаемой теме. Программа рассчитана на изучение материала V-VI классов за 1,5 учебных года, и поэтому в VI классе со II полугодия необходимо приступать к изучению материала VII класса.
В рамках V класса изучаются следующие темы: натуральные числа (повторение изученного в начальной школе), обыкновенные и десятичные дроби.
В VI классе: отрицательные и положительные числа, пропорции и проценты, решение уравнений и координатная плоскость.
5 КЛАСС
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА ПО КУРСУ «МАТЕМАТИКА» В 5-КЛАССЕ (ПО ЧЕТВЕРТЯМ).
I четверть 9*4 ч.=З6 ч.
| № уроков | Содержание | Кол-во уроков |
| 1-12 | Действия с натуральными числами. | 12 |
| 13-16 | Свойства действий с натуральными числами. | 4 |
| 17-20 | Решение уравнений. | 4 |
| 21-30 | Решение задач (типа «во ск.», «на ск.», больше-меньше; «на», «в», на движение). | 10 |
| 31 | Подготовка к контрольной работе. | 1 |
| 32 | Контрольная работа №1 | 1 |
| 33-36 | Десятичная система исчисления, меры длины. | 4 |
II четверть 7*4 ч.=28 ч.
| № уроков | Содержание | Кол-во уроков |
| 36-39 | Что такое десятичная дробь. Сравнение десятичных дробей. | 4 |
| 40-43 | Сложение и вычитание десятичных дробей. | 4 |
| 44-46 | Решение уравнений. | 3 |
| 47 | Подготовка к контрольной работе. | 1 |
| 48 | Контрольная работа № 2. | 1 |
| 49-52 | Умножение десятичных дробей. | 4 |
| 53-56 | Деление десятичных дробей. | 4 |
| 57-59 | Решение уравнений. | 3 |
| 60 | Подготовка к контрольной работе. | 1 |
| 61 | Контрольная работа № 3. | 1 |
| 62-63 | Округление десятичных дробей. Прикидка | 2 |
III четверть 10*4 ч.=40 ч.
| № уроков | Содержание | Кол-во уроков |
| 64-66 | Обыкновенная дробь. Сравнение на луче. | 3 |
| 67-68 | Правильные и неправильные дроби. Сравнение с 1. | 2 |
| 69-72 | Признаки делимости. Разложение на простые множители. НОД. | 4 |
| 73-76 | Основное свойство. Сокращение дробей. | 4 |
| 77-80 | Сложение, вычитание и сравнение дробей с одинаковыми знаменателями. | 4 |
| 81 | Подготовка к контрольной работе. | 1 |
| 82 | Контрольная работа №4. | 1 |
| 83-86 | НОК. Приведение к общему знаменателю. | 4 |
| 87-90 | Сравнение, сложение и вычитание дробей с разными знаменателями. | 4 |
| 91-93 | Решение уравнений. | 3 |
| 94 | Подготовка к контрольной работе. | 1 |
| 95 | Контрольная работа №5. | 1 |
| 96-99 | Умножение обыкновенных дробей. | 4 |
| 100-104 | Деление обыкновенных дробей. | 4 |
IV четверть 8*4 ч.=32ч.
| № уроков | Содержание | Кол-во уроков |
| 105-107 | Решение уравнений. | 3 |
| 108 | Подготовка к контрольной работе. | 1 |
| 109 | Контрольная работа №6. | 1 |
| 110-113 | Смешанные числа. | 4 |
| 114-117 | Три задачи на дроби. | 4 |
| 118-121 | Решение текстовых задач (составление уравнений, проценты). | 4 |
| 122 | Подготовка к контрольной работе. | 1 |
| 123 | Контрольная работа №7. | 1 |
| 124-127 | Все действия обыкновенными и десятичными дробями. | 4 |
| 128-134 | Повторение. Итоговая контрольная работа. | 7 |
6 КЛАСС
Из программы 6 класса осталось пройти следующие темы: «Положительные и отрицательные числа», «Решение уравнений», «Координатная плоскость», «Пропорция».
За I четверть изучаются положительные и отрицательные числа, координатная плоскость. Первые уроки четверти посвящаются повторению пройденного в 5 классе.
II четверть начинается с изучения темы: «Решение уравнений», а затем до конца четверти учащиеся занимаются нахождением неизвестного члена пропорции и решают задачи на прямую и обратную пропорциональную зависимость.
С окончанием II четверти заканчивается изучение материала 6-го класса.
Математика. 5 класс
Конспект урока
Перечень рассматриваемых вопросов:
Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы.
Правильные дроби – это дроби, в которых числитель меньше знаменателя
Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя.
Теоретический материал для самостоятельного изучения
Очень часто в жизни мы слышим такие выражения: «Прошел половину пути», «Купил четвертинку хлеба», «Сделал третью часть от работы». Все эти выражения связаны с новым понятием «дробь». О ней сегодня и пойдёт речь.
Чтобы ввести понятие дроби, выполним следующее задание.
Две части будут весить две третьих килограмма.
Если на отрезке АС укладывается ровно 3 раза отрезок длиной одна пятая сантиметра, то говорят, что длина отрезка равна три пятых сантиметра.
Такие записи называются обыкновенными дробями или просто дробями.
Дробь показывает какую-то часть от целого или единицы. Например, дробь семь восьмых показывает семь восьмых части от единицы.
Обозначенное таким образом число называют рациональным числом. При этом p называется числителем дроби (он всегда находится над чертой), а q – знаменателем дроби (он всегда находится под чертой).
Рассмотрим виды обыкновенных дробей. Обыкновенные дроби можно разделить на следующие виды – правильные, когда числитель меньше знаменателя, и неправильные, когда числитель равен или больше знаменателя.
Сколько часов содержится в четверти суток?
Так как в сутках 24 часа, то нам по условию надо найти четвёртую часть, т. е. разделить двадцать четыре часа на четыре части.
Решим задачу, используя понятие обыкновенной дроби.
В коробке находилось два вида конфет: 5 шоколадных и 6 карамелек. Какую часть всех конфет занимают карамель и шоколад?
Решение: для начала найдём общее количество конфет в коробке, для этого сложим все виды конфет.
5 + 6 = 11 – конфет в коробке.
Теперь можно найти, какую часть от общего количества конфет занимает карамель, а какую шоколадные конфеты. Для этого запишем результат в виде обыкновенной дроби, где в знаменателе укажем общее число конфет. Пять одиннадцатых – часть шоколадных конфет, а шесть одиннадцатых – часть карамели.
№ 1. Сколько минут содержится в одной трети часа?
Решение: для решения этой задачи достаточно вспомнить, что 1 ч = 60 мин.
Найдём третью часть от 60 минут, для этого:
№ 2. Длина отрезка АВ равна 10 см. Чему равен отрезок, длина которого составляет две пятых от длины отрезка АВ?
Решение: сначала найдём, чему равна одна часть из 5 отрезков.
10 см : 5 = 2 см – одна часть.
По условию задачи нужно найти 2 части из пяти, поэтому: 2 см · 2 = 4 см


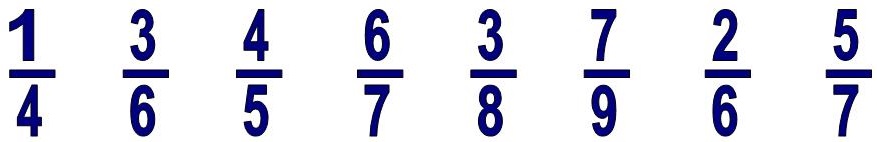







 , где – m числитель, а n – знаменатель.
, где – m числитель, а n – знаменатель.









