в каком классе изучают тригонометрию в школе
Изучение школьного курса тригонометрии в контексте ФГОС
ГБОУ гимназии № 000 Санкт-Петербурга
Изучение школьного курса тригонометрии в контексте ФГОС
В статье рассматривается роль тригонометрии в развитии мышления школьников, а также ее значимость для дальнейшего образования и практической деятельности.
Задача учителя – открывать новую перспективу размышлениям ученика.
Раздел школьного курса математики «Тригонометрия» неоднократно претерпевал изменения как по содержанию, так и по количеству часов на его изучение. Так, до 1966 года в 9-х и 10-х классах изучалась отдельная дисциплина «Тригонометрия». Изучение курса строилось в той логической последовательности, в которой «осваивало тригонометрические закономерности человечество: от практических измерений – к формальным положениям науки, в полном соответствии с идеей » [1]. Таким образом, с помощью тригонометрии ребенок имел возможность «примерить» на себя математический стиль мышления, просканировать свою предрасположенность, свой интерес к человеческой деятельности такого рода. С реформой тригонометрия перестала рассматриваться как педагогический инструмент развития мышления, приобщения ребенка к основам научной картины мира. И, к сожалению, индуктивный характер изучения тригонометрии стал уступать место формально-логическому. В результате, тригонометрический материал стал постепенно «выжиматься» не только из основной школы, но и из курса старшей ступени.
Сейчас, с одной стороны, возвращается прежний, разумный порядок ее изучения: в основной школе изучается тригонометрия треугольника, а в средней школе тригонометрия составляет целостный раздел курса алгебры и начал анализа, с другой стороны, при том количестве часов, которое уделяется на эту тему, ученикам не хватает времени на вдумчивое и глубокое ее освоение.
В то же время тригонометрический материал входит в ЕГЭ и используется при проведении всевозможных олимпиад и конкурсов. Соответственно не снижается потребность определенной части учащихся в глубоком знании тригонометрии.
Поэтому так важна методически грамотная организация изучения данного раздела, способствующая формированию универсальных учебных действий учащихся – одной из целей ФГОС второго поколении, в которых наряду с предметными выделяются также метапредметные и личностные образовательные результаты.
Для достижения необходимых результатов использую в своей работе системно-деятельностный подход. Учу своих учеников отвергать «знания, приобретенные путем простого зубрения», и приветствовать «умственный материал, набираемый памятью постепенно, день за днем, в связи с различными контекстами, связанный ассоциативно с другими внешними событиями и неоднократно подвергшийся обсуждению» [2]. Активно использую на уроках исторические сведения, так как «экскурсы в историческое прошлое оживляют урок, дают разрядку умственному напряжению, поднимают интерес к изучаемому материалу и способствуют прочному его усвоению» [3].
Практика показывает, что основная проблема изучения тригонометрии в школе связана с освоением идеи «числовой окружности» и введением тригонометрических функций числового аргумента. Считаю, что в школьной программе не уделяется должного внимания освоению идеи единичной окружности, а практическое решение проблемы доверяется учителю, его методическому «чутью».
Убеждена, что преподавателю необходимо так организовать изучение материала, чтобы у учащихся возникли отчетливые геометрические представления, связанные с единичным кругом. Это требование может показаться, на первый взгляд, усложнением задачи преподавания, однако затраченное время с избытком окупится позже.
Второй этап – изучение темы «Элементы тригонометрии» (алгебра, 9 класс). Согласна с точкой зрения об индуктивном изучении тригонометрии. Поэтому основную цель освоения данной темы вижу в плавном переходе к тригонометрии любого угла. И снова особое место отвожу изучению «тригонометрического» круга, так как воспроизведение его мысленно или на бумаге и знание теоремы Пифагора закладывают основу не только теории тригонометрии острого угла, но и теории тригонометрических функций любого действительного аргумента. В результате ученик получает возможность непосредственно увидеть справедливость изученных формул тригонометрии. В противном случае, он обречен на заучивание всех этих формул без достаточной мнемонической основы и оказывается в беспомощном положении, если та или иная формула ускользает из его памяти.
Остановлюсь более подробно на описании действий, направленных на решение указанной задачи в рамках двух тем. При изучении темы «Понятие угла» учащиеся учатся отмечать на пересечении единичной окружности и осей координат «опорные» точки, соответствующие углам 0̊, 90̊, 180̊, 270̊; потом точки, соответствующие углам 45̊, 135̊, 225̊,315̊ (получаемые делением пополам координатных углов); затем точки, получаемые делением пополам вертикальных радиусов единичной окружности (30̊, 150̊, 210̊, 330̊), и, наконец, точки, получаемые делением пополам горизонтальных радиусов единичной окружности (60̊, 120̊, 240̊, 300̊). Изображению точек во втором и в третьем случаях помогает опора на интуитивно ясное свойство синуса острого угла: с увеличением угла от 0̊ до 90̊ значения синуса угла увеличиваются (принимая каждое свое значение только один раз). Учащиеся формулируют выводы: например, так как sin 30̊ = 0,5, то если на рисунке изображен острый угол, «синус» которого равен 0,5, этот угол содержит 30̊. Затем десятиклассникам предлагаются небольшие самостоятельные работы, результаты которых напрямую зависят от тщательной отработки изучаемого материала. Так как материал излагается с опорой на ранее изученное, то у учащихся появляется возможность получить хорошие отметки за большое число несложных, но важных работ.
При изучении темы «Радианная мера угла» ученики обычно недопонимают необходимость выражать число радиан через число «пи». Чтобы снять всякие сомнения на этот счет, вместе с учениками откладываем углы в 1, 2, 3, 4, 5, 6 радиан (при этом необходимо откладывать 1, 2, 3, 4, 5, 6 раз дугу, равную ее радиусу). Эмпирическим путем получаем: ни одно новое деление не совпадет со старым. Таким образом, становится ясно, что число 



В итоге, можно надеяться на успешное решение простейших тригонометрических уравнений, так как умение правильно изображать на единичной окружности точки, соответствующие «табличным» значениям тригонометрических функций, должно быть сформировано.
В заключение хочется отметить, что учащиеся, независимо от профиля школы, должны получить опыт «создания» фрагмента науки. А тригонометрия для этого является наиболее естественным разделом школьной математики. И поэтому каждый учитель математики должен определить свое отношение к этим возможностям тригонометрии.
2. Подласый : Новый курс: учеб. для студ. пед. вузов: в 2 кн. М.: Гуманист: Владос, 2000. – кн.1: Общие основы. Процесс обучения. – С.36.
3. Малыгин историзма в преподавании математики в средней школе. – М.: «Учпедгиз», 1956. – С. 3.
В каком классе изучают тригонометрию?
10-11. советую учить и запоминать все, что вам скажет учитель, потому что иначе будет все грустно и о хороших баллах на егэ можно будет забыть
Во первых есть какие-то определенные обычаи в школах,как переход из начальных классов в старшие классы.Поэтому принято делать выпускной в четвертом классе.Но это вопрос родителей.Если родители считают нужным,они организуют выпускной для своих детей и учителей,а если не считают,то можно и без выпускного обойтись.
Известны случаи,когда одни родители старались сделать выпускной дороже,устраивали его в кафе и даже в ресторанах и было скучно,а другие в школе с участием тамады и сладкого стола и было весело и не дорого.
Скорей всего, Вы имеете в виду не исторические, а политические взгляды Л.Н. Толстого. В рассказе «После бала» автор резко противопоставляет добродушие полковника на балу, где он выступает в роли отца, и его жестокость в сцене с солдатом, где отец возлюбленной героя становится олицетворением системы. Стоит напомнить, где действия рассказа происходит во времена царствования императора Николая I, известного своей жестокостью.
Последний звонок обычно бывает в последних числах мая.
В походы, наверное, ходят, но намного реже, не так как раньше. И скорее всего ходят те, кто живёт и учиться не в столице и больших городах, кто живёт в маленьком городе, где относительно близко лес и горы. И ещё очень многое в этом вопросе зависит от классного руководителя и активности хотя бы некоторых родителей, которым не безразлично, то как растёт,учится, развивается и отдыхает их ребенок.
Тригонометрия с нуля: основные понятия, история
Синус, косинус, тангенс – при произнесении этих слов в присутствии учеников старших классов можно быть уверенным, что две трети из них потеряют интерес к дальнейшему разговору. Причина кроется в том, что основы тригонометрии в школе преподаются в полном отрыве от реальности, а потому учащиеся не видят смысла в изучении формул и теорем.
В действительности данная область знаний при ближайшем рассмотрении оказывается весьма интересной, а также прикладной – тригонометрия находит применение в астрономии, строительстве, физике, музыке и многих других областях.
Ознакомимся с основными понятиями и назовем несколько причин изучить этот раздел математической науки.
История
Неизвестно, в какой момент времени человечество начало создавать будущую тригонометрию с нуля. Однако документально зафиксировано, что уже во втором тысячелетии до нашей эры египтяне были знакомы с азами этой науки: археологами найден папирус с задачей, в которой требуется найти угол наклона пирамиды по двум известным сторонам.
Предполагается, что знаменитая теорема Пифагора, относящаяся к основам тригонометрии, была известна вавилонянам почти четыре тысячи лет назад.
Название
Дословно термин «тригонометрия» можно перевести как «измерение треугольников». Основным объектом изучения в рамках данного раздела науки на протяжении многих веков был прямоугольный треугольник, а точнее – взаимосвязь между величинами углов и длинами его сторон (сегодня с этого раздела начинается изучение тригонометрии с нуля). В жизни нередки ситуации, когда практически измерить все требуемые параметры объекта (или расстояние до объекта) невозможно, и тогда возникает необходимость недостающие данные получить посредством расчётов.
Например, в прошлом человек не мог измерить расстояние до космических объектов, а вот попытки эти расстояния рассчитать встречаются задолго до наступления нашей эры. Важнейшую роль играла тригонометрия и в навигации: обладая некоторыми знаниями, капитан всегда мог сориентироваться ночью по звездам и скорректировать курс.
Основные понятия
Для освоения тригонометрии с нуля требуется понять и запомнить несколько основных терминов.
Тангенс – это отношение противолежащего катета к прилежащему (либо, что то же самое, отношение синуса к косинусу). Котангенс – это единица, деленная на тангенс.
Стоит упомянуть и знаменитое число Пи (3,14…), которое представляет собой половину длины окружности с радиусом в одну единицу.
Популярные ошибки
Люди, изучающие тригонометрию с нуля, совершают ряд ошибок – в основном по невнимательности.
Во-первых, при решении задач по геометрии необходимо помнить, что использование синусов и косинусов возможно только в прямоугольном треугольнике. Случается, что учащийся «на автомате» принимает за гипотенузу самую длинную сторону треугольника и получает неверные результаты вычислений.
В-третьих, пока задача полностью не решена, не стоит округлять какие бы то ни было значения, извлекать корни, записывать обыкновенную дробь в виде десятичной. Часто ученики стремятся получить в задаче по тригонометрии «красивое» число и сразу же извлекают корень из трёх, хотя ровно через одно действие этот корень можно будет сократить.
Этимология слова «синус»
История слова «синус» поистине необычна. Дело в том, что буквальный перевод этого слова с латыни означает «впадина». Всё потому, что верное понимание слова затерялось при переводе с одного языка на другой.
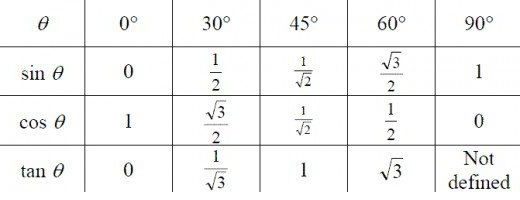
Таблицы значений
Существуют таблицы, в которые занесены числовые значения для синусов, косинусов и тангенсов всех возможных углов. Ниже представим данные для углов в 0, 30, 45, 60 и 90 градусов, которые необходимо выучить как обязательный раздел тригонометрии для «чайников», благо запомнить их довольно легко.
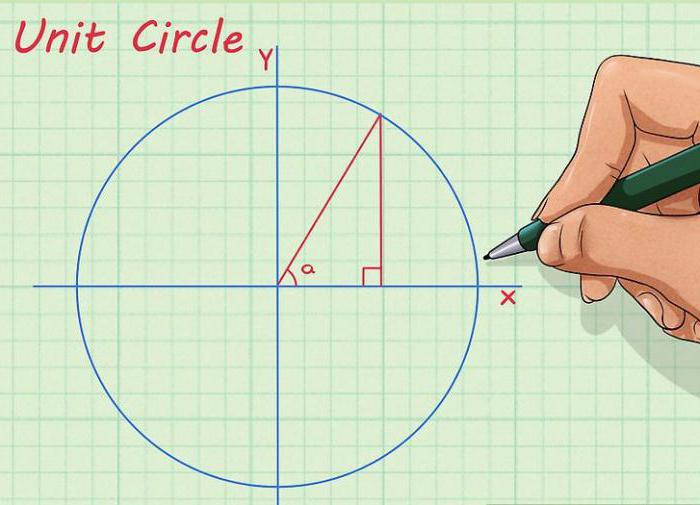
Геометрическое представление
Начертим круг, через его центр проведем оси абсцисс и ординат. Ось абсцисс располагается горизонтально, ось ординат – вертикально. Обычно они подписываются как «X» и «Y» соответственно. Теперь из центра окружности проведем прямую таким образом, чтобы между ней и осью X получился нужный нам угол. Наконец, из той точки, где прямая пересекает окружность, опустим перпендикуляр на ось X. Длина получившегося отрезка будет равна численному значению синуса нашего угла.
Применение
Одними из первых специалистов, использующих тригонометрию, были моряки, не имеющие никакого другого ориентира в открытом море, кроме неба над головой. Сегодня капитаны кораблей (самолётов и других видов транспорта) не ищут кратчайший путь по звёздам, зато активно прибегают к помощи GPS-навигации, которая без использования тригонометрии была бы невозможна.
Практически в каждом разделе физики вас ждут расчёты с использованием синусов и косинусов: будь то приложение силы в механике, расчёты пути объектов в кинематике, колебания, распространение волн, преломление света – без базовой тригонометрии в формулах просто не обойтись.
Ещё одна профессия, которая немыслима без тригонометрии – это геодезист. Используя теодолит и нивелир либо более сложный прибор – тахиометр, эти люди измеряют разницу в высоте между различными точками на земной поверхности.
Повторяемость
В заключение
Задумываясь о том, как выучить тригонометрию, большинство учащихся средней и старшей школы начинают считать её сложной и непрактичной наукой, поскольку знакомятся лишь со скучной информацией из учебника.
Рабочая программа «Основы тригонометрии»
Ищем педагогов в команду «Инфоурок»
(пропедевтический элективный курс 1 час в неделю)
Особенности программного материала.
Математика, давно став языком науки и техники, в настоящее время все шире проникает в повседневную жизнь и обиходный язык, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требуют математической грамотности человека на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления.
В частности, важным аспектом является изучение тригонометрии – как автономной ветви математики. Учение о тригонометрических функциях имеет широкое применение во многих областях современной науки.
Раздел “Тригонометрия” школьного курса математики традиционно наиболее сложный для обучающихся. В 9 классе по геометрии школьники имеют лишь поверхностное представление о тригонометрических функциях, а вычисление их значений некоторых углов (особенно тупых) и вовсе происходит на интуитивном непонятном для детей уровне. Тем не менее, задачи по тригонометрии включаются в модуль «Геометрия» на ГИА-9 и большая часть сдающих допускает много ошибок при выполнении заданий именно этого раздела или вообще не берется за такие задания. Разработанный элективный курс «Основы тригонометрии» способствует решению этой проблемы, так как подбор задач будет осуществляться из открытого банка заданий ГИА-2018.
Кроме того, данный курс является пропедевтическим для тех, кто планирует продолжить свое обучение в старшей школе. В 10 классе большая часть времени отводится изучению тригонометрии, но недостаточное количество программных часов и обилие информации также не позволяют сформировать у обучающихся системные качественные знания и практические навыки.
Эти недостатки в получении тригонометрических знаний помогает устранить данный элективный курс.
2. Требования к знаниям и умениям учащихся в 9 классе.
В результате изучения материала данного курса предполагается, что обучающиеся 9 классов не только усвоят основные алгоритмы и правила решения тригонометрических заданий, но и будут понимать смысл важнейших понятий и их свойств, будут уметь решать задачи, не сводящиеся к прямому применению алгоритма, научатся применять полученные знания и умения в заданиях с практическим контекстом, знакомым учащимся или близким их жизненному опыту.
3. Целевая установка.
Целью прохождения настоящего курса является: повторение, систематизация, активизация знаний школьного курса тригонометрии; расширение знаний учащихся по курсу; приобретение конкретных практических навыков решения тригонометрических заданий в процессе подготовки к ГИА-2018.
Задачи: Повторить и обобщить имеющиеся знания; расширить, углубить знания по тригонометрии; подготовить 9классников к государственной итоговой аттестации.
4. Структура программы.
В структуре программы элективного курса 9 класса выделяются следующие основные разделы:
Тригонометрия в треугольнике
Тригонометрия на окружности.
5. Формы организации учебного процесса.
Для реализации данного курса используются различные формы организации занятий: групповая, индивидуальная, работа в парах. Большая часть времени будет уделена практическим занятиям, посвященным решению задач, в том числе и физических.
6. Итоговый контроль.
7. Объем и сроки изучения.
Программа общим объемом 17 часов изучается во втором полугодии учебного года (по 1 часу в неделю).
Календарно – тематическое планирование
Элективный курс 9 класс
Содержание учебного материала
ТРЕТЬЯ ЧЕТВЕРТЬ (с 10.01.2018 по 24.03.2018)
Тригонометрия в треугольнике.
Как измерить крутизну. Понятие синуса.
Тангенс. Косинус. Нахождение углов.
Решение задач «Тригонометрия в прямоугольном треугольнике»
Решение треугольников (теорема синусов, косинусов)
ЧЕТВЕРТАЯ ЧЕТВЕРТЬ (с 02.04.2018 по 25.05.2018)
Тригонометрия на окружности.
Часы, или современный взгляд на тригонометрию. Понятие тригонометрического круга.
Тригонометрические функции на единичной окружности. Знаки тригонометрических функций. Ось тангенсов.
Как не учить формулы! (мнемонические правила использования формул приведения) Решение задач.
Вокруг площади треугольника (решение задач)
Итоговый урок (защита рефератов, представление презентаций)
Список литературы и интернет-ресурсов
И.М.Гельфанд, С.М.Львовский, А.Л. Тоом «Тригонометрия»
МЦНМ АО «Московские учебники» Москва 2002
Открытый урок-игра. Тема «Ох уж эта тригонометрия»
Разделы: Математика
1. Портреты ученых математиков.
«Математика- это язык, на котором говорят все точные науки».
Н.И. Лобачевский.
Пускай кому- то мил английский,
Кому – то химия важна,
Без математики же всем нам
Но ни туда и ни сюда
Нам уравнения, как поэмы
И синусы поддерживают дух
Нам косинусы, будто песни,
А формулы приведения
Ласкают слух.
Говорит она беззвучно
Но понятно и не скучно,
Ты беседуй чаще с ней
Станешь лучше и умней.
В ней мало слов, в ней много цифр и знаков
И вид страниц как будто одинаков,
Но на страницах жизнь отражена,
А жизнь разнообразием полна.
(Тетрадь по математике).
Конкурс: Из истории математики. (это задание было дано заранее учащимся).
Команда 1: Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны простейшие сведения из тригонометрии. Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников». Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц.
Важный вклад в развитие тригонометрии был внесен индийской математикой в период 5- 12 век нашей эры. Индийские математики стали вычислять не полную хорду, как это делали греки, а ее половину (то есть «линию синусов»). Линия синусов именовалась ими «архаджива», буквально означало «половина тетивы лука». Индийцы составили таблицу синусов, в которой были даны значения полухорд, измеренных частями (минутами) окружности для всех углов от 0 до 90 градусов. Индийским математикам были известны соотношения, которые в современных обозначениях пишут так:
Команда 2: В 15- 17 веках в Европе было составлено и издано несколько тригонометрических таблиц, над их составлением работали крупнейшие ученые:
В России первые тригонометрические таблицы были изданы в 1703 году при участии Л.Ф. Магницкого.
На первоначальных стадиях своего развития тригонометрия служила средством решения вычислительных геометрических задач. Ее содержанием считалось вычисление элементов простейших геометрических фигур, то есть треугольников. Таким образом, тригонометрия возникла на геометрической основе, имела геометрический язык и применялась к решению геометрических задач.