в каком классе изучают сокращение дробей
Презентация по математике на тему «Сокращение дробей» (6 класс)
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
Описание слайда:
Сокращение дробей
Выполнила: учитель математики
Боровская НИ
Описание слайда:
Один мудрец однажды сказал: “Не для школы, а для жизни мы учимся!”
Описание слайда:
Устный счёт
12,4 : 4 =
0,3 0,15 =
3,5 : 0,05 =
1,7 0,03 =
4 : 0,001 =
12,5 – 3,05 =
45,6 + 1,02 =
18,04 – 2,04 =
3,1
0,045
70
0,051
4000
9,45
46,62
16
Описание слайда:
Разминка
Найдите равные дроби
Описание слайда:
Назовите дроби, равные данной
9
30
45
16
Описание слайда:
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
3
3
Сокращение дроби
3
17
Описание слайда:
Несократимая дробь
Дробь сократить нельзя, если её числитель и знаменатель
взаимно простые числа.
НОД(3;17) = 1
Описание слайда:
Найди несократимые дроби. Нажмите на букву
рядом с несократимыми дробями.
У
М
Ы
Н
И
Ц
Ш
Я
0,3
0,23
0,8
0,1
С
0,25
Описание слайда:
Сокращение дроби при помощи разложения на множители
Описание слайда:
Сокращение дроби на
наибольший общий делитель
2
5
НОД(110; 275)
110
275
= 1011
= 2 5 11
= 2511
= 5511
= 511 = 55
Сократим на 55
Описание слайда:
Последовательное сокращение дроби
22
55
2
5
Сократим на 5
Сократим на 11
Верно ли, что дробь при таком сокращении становится все меньше и меньше.
Описание слайда:
Работа в группах
Сократить дробь
1. Сократить числитель и знаменатель на их НОД
2. Последовательно сокращать на общие делители
3. Разложить числитель и знаменатель на множители,
а потом сократить
Описание слайда:
Один рабочий изготовил 16 одинаковых деталей за 6 ч, а другой 24 такие же детали за 15 ч.
Какой из них тратил на изготовление 1 детали больше времени?
Найдите скорость работы каждого рабочего.
Описание слайда:
Из 52 м полотна сшили 10 пододеяльников,
а из 33 м – 15 простыней. Сколько полотна идет на комплект, в который входит 1 простыня и 1 пододеяльник.
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Краткое описание документа:
Данный материал можно использовать на уроке математики в 6 классе на этапе изучения нового материала или повторения изученного.
Общая информация
Международная дистанционная олимпиада Осень 2021
Похожие материалы
Презентация по математике (4класс)
Рабочая программа по математике 5-6 класс
Рабочая программа по математике 10-11 класс профильный уровень
Презентация по математике на тему «Задачи «на части» » (5 класс)
«Интерактивные образовательные платформы как средства формирования функциональной грамотности»
Спецификация итоговой контрольной работы по математике
Банк развивающих электронных игр по математике для начальной школы
Межпредметные связи на уроках математики в условиях ФГОС ООО
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5267574 материала.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
Роспотребнадзор продлил действие санитарных правил для школ
Время чтения: 1 минута
Новый ГОСТ на окна с защитой для детей вступает в силу 1 ноября
Время чтения: 1 минута
В Приамурье начнут пускать на занятия только привитых студентов
Время чтения: 0 минут
В Туве предложили ввести антиковидные паспорта для школьников
Время чтения: 2 минуты
«Спутник» объявили словом года в России
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Сокращение обыкновенных дробей
Что такое «сокращение дробей»
Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.
Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.
В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.
С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:


где a, b, m — натуральные числа.
Графически сокращение дробей обычно записывается вот так:
Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.
Пример 1. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 3.

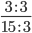
Сокращение выполнено: 
Пример 2. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 2.

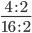
Сокращение выполнено: 
Приведение дробей к несократимому виду
Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.
Так, в результате сокращения в примере 2, мы из дроби 
Выходит, что дробь выдержит еще одно сокращение и придет к виду
Сокращая дробь, стремитесь в итоге получить несократимую дробь.
Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.
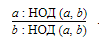
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.
Пример 3. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 12
Найдем частное: 12 : 12 = 1

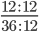
Сокращение выполнено: 
Пример 4. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 5
Найдем частное: 15 : 5 = 3

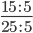
Сокращение выполнено: 
Правило сокращения дробей
Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.
Выполняйте сокращение дробей по следующему алгоритму:
В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.
Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.
Пример 5. Сократите дробь
Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5
Мысленно убираем все общие множители и перемножаем оставшиеся.

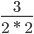
Сокращение выполнено: 
Пример 6. Сократите обыкновенную дробь
Найдем НОД числителя и знаменателя. НОД = 9

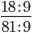
Сокращение выполнено: 
Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.
Пример 6. Сократите дробь:

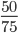
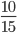
Сокращение выполнено: 
Пример 7. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
168 = 2 * 2 * 2 * 3 * 7
240 = 2 * 2 * 2 * 2 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24
НОД 168 и 240 равен 24
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

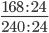
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
360 = 2 * 2 * 2 * 3 * 3 * 5
540 = 2 * 2 * 3 * 3 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180
НОД 360 и 540 равен 180
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

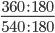
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
420 = 2 * 2 * 3 * 5 * 7
2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420
НОД 420 и 2520 равен 420
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

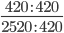
Сокращение выполнено. Дробь приведена к несократимому виду: 
Пример 9. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
1575 = 3 * 3 * 5 * 5 * 7
3450 = 2 * 3 * 5 * 5 * 23
Перемножаем все общие множители между собой 3 * 5 * 5 = 75
НОД 1575 и 3450 равен 72
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

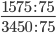
Сокращение выполнено. Дробь приведена к несократимому виду: 
Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.
Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.
Урок математики в 6-м классе на тему «Сокращение дробей»
Разделы: Математика
Ход урока
I. Устный счет: “МАТЕМАТИЧЕСКАЯ ЗАРЯДКА”.
Задание написано на доске, учащиеся должны определить, какое из равенств является верным, а какое нет. Учитель показывает физические упражнения, которые соответствуют ответу “да” и “нет”, а дети показывают то из них, которое означает, на их взгляд, правильный ответ.
ВЕРНО ЛИ РАВЕНСТВО:
а)
;
б);
в);
г);
д);
е);
ж);
з)?
II. Игра: “КТО БЫСТРЕЕ СЯДЕТ В РАКЕТУ”.
а) На каком свойстве основано сокращение дробей?
б) Какая дробь называется несократимой?
в) Что меняется при сокращении дроби?
а)
;
б);
в).
а)
;
б);
в).
4. Найдите сумму дробей и сократите результат:
а)
;
б);
в).
5. Сократите неправильную дробь, и затем выделите из нее целую часть:
а)
;
б);
в).
6. Какую часть прямого угла составляет угол, равный:
7. Какую часть метра составляют
III. Закрепление.
На доске записаны выражения, а под ними ответы, но не по порядку. Ученики должны найти для каждого выражения правильный ответ. Несколько учеников работают на переносных досках, а все остальные на местах.
СОКРАТИТЕ ДРОБНОЕ ВЫРАЖЕНИЕ:
а)
;
б);
в);
г);
д);
е);
ОТВЕТЫ: 1,2; 0,1; 0,5; 1; 3; 0,5.
IV. Домашнее задание.
Учебник “Математика 6” стр.41 (ответить на вопросы 1 и 2), № 281, 282.
V. Самостоятельная работа.
Детям раздается дидактический материал.
| 1 вариант | 2 вариант | 3 вариант | 4 вариант |
а)  | а)  | а)  | а)  |
б)  | б)  | б)  | б)  |
в)  | в)  | в)  | в)  |
2. СОКРАТИТЕ ДРОБНОЕ ВЫРАЖЕНИЕ:
| 1 вариант | 2 вариант | 3 вариант | 4 вариант |
а)  | а)  | а)  | а)  |
б)  | б)  | б)  | б)  |
в)  | в)  | в)  | в)  |





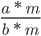
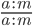
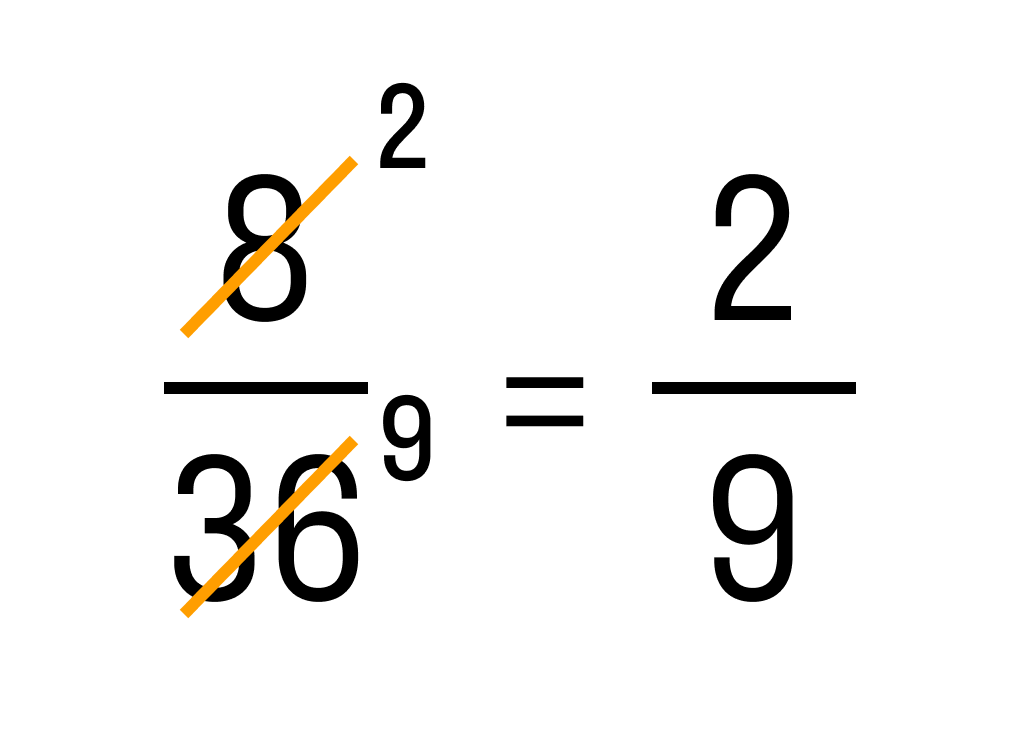
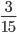
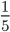
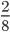
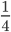
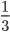
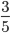
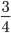
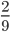
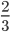
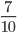
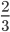
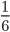
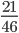
 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ?
? ;
;  ;
;  ;
;  .
. ;
;  ;
;  .
. ;
;  ;
;  .
. ;
;  ;
;  ;
;  ;
;  ;
;  ;
;