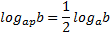в каком классе изучают логарифмы в школе
Изучение логарифмов в старшей школе
Понятие логарифма
При решении показательных уравнений удается представить обе части уравнения в виде степеней с одинаковыми основаниями и рациональными показателями. Так, например, при решении уравнения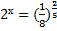 
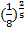
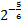
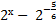
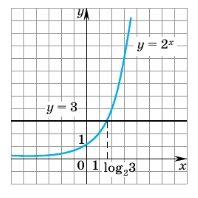
мы заменяем 
степенью 
и из равенства степеней с одинаковыми основаниями 
делаем вывод о равенстве показателей: х = −5/6. Однако, чтобы решить, казалось бы, более простое уравнение 2 х = 3, стандартных знаний оказывается недостаточно. Дело в том, что число 3 нельзя представить в виде степени с основанием 2 и рациональным показателем.
С другой стороны, график непрерывной функции y = 2 x пересекается с прямой y = 3, и, значит, уравнение 2 x = 3 имеет корень. Таким образом, перед нами стоят два вопроса: «Как записать этот корень?» и «Как его вычислить?».
Показатель степени, в которую нужно возвести число a (a > 0, a ≠ 1), чтобы получить число b, называется логарифмом b по основанию a и обозначается logab.
Теперь мы можем записать корень уравнения 2 х = 3:
Равенства a x = b и x = logab, в которых число a положительно и не равно единице, число b положительно, а число x может быть любым, выражают одно и то же соотношение между числами a, b и x. Подставив в первое равенство выражение x из второго, получим основное логарифмическое тождество.
Понятие логарифма в методическом пособии
Задание
Решите уравнение: а) 2 x = 64; б)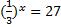 
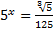
; в) 
; г) 4 x = 0; д) 7 x = −12.
После проверки ученикам предлагается ответить на вопрос, какое из заданий показалось им наиболее трудным. Вероятный ответ: 2 (в), так как в нем нужно было приводить дробь к степени числа 5. Затем школьникам предлагается высказать мнение о сравнительной с заданием 2 (в) трудности уравнения 2 x = 3. На первый взгляд кажется, что это уравнение проще, однако представить 3 в виде степени числа 2 школьникам не удается.
После этого диалог с классом можно строить примерно так:
— Как вы думаете, имеет ли уравнение 2 x = 3 корень? Ответ обоснуйте. [Если построить график функции у = 2 x и провести прямую у = 3, то они пересекутся в одной точке, значит, уравнение имеет один корень.]
— Что можно сказать о корне уравнения a x = b, где а > 0 и а ≠ 1? При всех ли значениях b оно имеет корни?
Затем вводится определение логарифма числа b по основанию а и записывается основное логарифмическое тождество 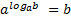. При этом выписывание равенства происходит синхронно с повторным чтением определения теперь уже в обратном, по сравнению с учебником, порядке. Теперь можно записать корень уравнения 2 х = 3: х = loga3 и предложить школьникам серию самостоятельных работ.
Логарифмическая функция
Показательная функция x = a y является монотонной, и, значит, разные значения y соответствуют разным значениям x, но это говорит о том, что y = logax, в свою очередь, является функцией x.
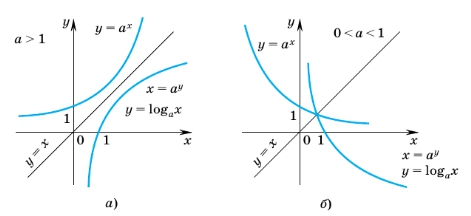
Показательная функция y = a x и логарифмическая функция y = logax являются взаимно обратными. Сравнивая их графики, можно отметить некоторые основные свойства логарифмической функции.
Свойства функции y = logax, a > 0, a ≠ 11:
Решение логарифмических уравнений и неравенств на основе свойств логарифмической функции
Освобождаясь от внешнего логарифма, имеющего основание 3, мы ссылаемся на возрастание соответствующей логарифмической функции, то есть на то, что большему значению логарифма соответствует большее значение выражения, стоящего под его знаком. Однако следует иметь в виду, что если функцию y = log3 log0,5(2x + 1) считать логарифмической, то ее аргумент не переменная x, а все выражение log0,5(2x + 1). Если же все-таки рассматривать x как аргумент функции y = log3 log0,5(2x + 1), то эта функция окажется убывающей, так как при увеличении значения x увеличивается значение выражения 2x + 1, уменьшается значение выражения log0,5(2x + 1) и, соответственно, уменьшается значение самой функции.
Свойства логарифмов
Связь двух форм записи соотношения между числами a, b и x (речь о a x = b и x = logab) позволяет получить свойства логарифмов, основываясь на известных свойствах степеней.
Заметим, что в левой части формулы числа a и b могут быть отрицательными. Тогда формула будет выглядеть так:
Аналогично можно получить еще два свойства для логарифмов частного и степени.
Последнее свойство дает возможность вывести важную формулу, с помощью которой можно выразить логарифм с одним основанием через логарифм с другим основанием.
Пусть logab = x. Перейдем к показательной форме a x = b. Прологарифмируем это равенство по основанию c, т.е. найдем логарифмы с основанием c обеих частей этого равенства: logca x = logcb. Применяя к левой части свойство логарифма степени, получим x logca = logcb или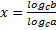 
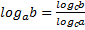
, откуда 
.
Формула перехода от одного основания логарифма к другому
Полезно запомнить частный случай формулы перехода, когда одно из оснований является степенью другого:
Рассмотренные свойства и формула перехода «работают», конечно, только когда все входящие в них выражения имеют смысл.
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок № 24. Логарифм. Свойства логарифмов.
Перечень вопросов, рассматриваемых в теме
1. Определение логарифма.
2. Основное логарифмическое тождество.
3. Свойства логарифмов.
Логарифмом положительного числа 
по основанию 
, 
называется показатель степени, в которую надо возвести 
чтобы получить 
.
Логарифмирование – это действие нахождения логарифма числа.
Основное логарифмическое тождество: 
Свойства логарифмов. При 
, 
справедливы равенства:
— логарифм произведения: 
;
— логарифм частного: 
;
— логарифм степени: 
.
Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. – М.: Просвещение, 2014. – 384 с.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
При решении простейших показательных уравнений не всегда можно найти точный ответ. Например, уравнение 
имеет корень 5, т. к. 
значит 
, 
В уравнении 
число 5 не является степенью 2, значит предыдущий способ решения не подходит. Нам известно, что уравнение имеет единственный корень. Посмотрим это на графике.
Абсцисса точки пересечения – единственное решение данного уравнения. Это число и называют логарифмом 5 по основанию 2.
Дадим определение логарифма.
Логарифмом положительного числа 
по основанию 
, 
называется показатель степени, в которую надо возвести 
чтобы получить 
.
Т. е. логарифм числа 
по основанию 
, 
есть некоторое число 
такое, что 
.
, т. к. выполнены все условия определения:
1) 216 > 0; 2) 6 > 0, 6 ≠ 1; 3) 
.
, т. к. выполнены все условия определения:
1) 
; 2) 2 > 0, 2 ≠ 1; 3) 
.
Это действие называется логарифмированием.
Логарифмирование – это действие нахождения логарифма числа.
Существует краткая запись определения логарифма: 
так называемое основное логарифмическое тождество. Его используют при вычислениях.
(Читают: 4 в степени логарифм 5 по основанию 4 равен 5)
(Читают: одна треть в степени логарифм 6 по основанию одна треть равен 6)
Решим несколько задач с использованием определения логарифма.
Задача 1. Вычислить 
.
Задача 2. Вычислить 
.
Решение. Для вычисления воспользуемся свойствами степеней: 1) 
, 2) 
и основным логарифмическим тождеством: 
.
.
Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотрим их.
1. Логарифм произведения.
Логарифм произведения чисел 
по основанию 
равен сумме логарифма 
по основанию 
и логарифма 
по основанию 
.
2. Логарифм частного.
Логарифм частного чисел 
по основанию 
равен разности логарифма 
по основанию 
и логарифма 
по основанию 
.
3. Логарифм степени.
Логарифм числа 
по основанию 
равен произведению показателя 
и логарифма 
по основанию 
.
Важно! Свойства выполняются при 
, 
Примеры и разбор решения заданий тренировочного модуля
№ 1. Вычислите: 
.
Чтобы выполнить это задание нам понадобятся следующие определения и свойства:
Представим 
в виде степени с рациональным показателем: 
. Далее воспользуемся свойством нахождения логарифма степени: 
. Вспоминаем таблицу квадратов: 
, значит 
, 
. Ответ: 
.
Чтобы выполнить это задание нам понадобятся следующие определения и свойства:
.