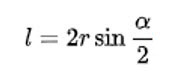в каком классе изучают хорды

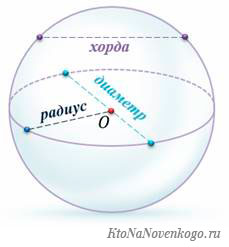
Хорда — это геометрическая струна

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы подробно расскажем, что такое ХОРДА.

Слово это имеет древнегреческие корни и переводится как «струна».

Это очень точно характеризует ее внешний вид, так как хорда представляет собой прямую линию.

Хорда — это.

Термин ХОРДА применяется сразу в нескольких областях:

В геометрии хорда – это часть прямой, которая проходит между двумя точками на окружности или эллипсе;

Но в рамках этой статьи мы подробно рассмотрим первый вариант значения термина ХОРДА. Тот, который применяют в геометрии, и который школьники подробно изучают в 7 классе.

Что такое хорда в геометрии

Хорда – это отрезок прямой, которая проходит через две точки на любой кривой линии. Это могут быть окружность, эллипс, гипербола или парабола.

Выглядит хорда вот так:

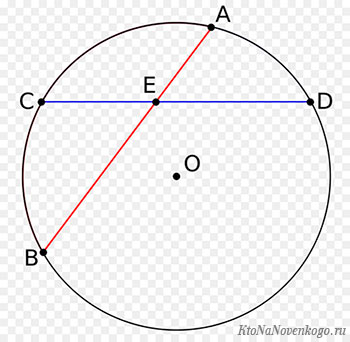
На этом рисунке изображены сразу две хорды – AB и CD. А есть еще частный случай, когда хорда проходит через центр окружности.

Такая хорда, на данном рисунке это отрезок AB, будет являться диаметром окружности. И как нетрудно догадаться, это самая длинная хорда, которая может быть для данного примера.

Свойства хорды

Если сравнивать хорду с другими частями окружности, то можно вывести целый ряд закономерностей.

Например, хорда и радиус:

Хорда и диаметр:

Хорда и центр окружности:

И еще одно свойство хорд в окружности. Если взять уже знакомый нам рисунок расположенный сразу под определением, то при пересечении хорд получается вот такая зависимость – произведение частей одной хорды равна произведению частей другой:

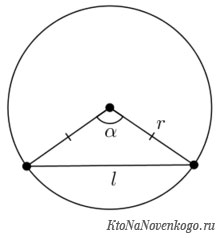
Как рассчитать длину хорды

Длина хорды – это расстояние от одной точки пересечения с окружностью до другой. Чаще всего она обозначается латинской буквой «L».

Чтобы рассчитать длину хорды, надо знать значение радиуса и центрального угла. Формула выглядит так:

Вот и все, что мы хотели рассказать о ХОРДЕ.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Не знаю, что делать школьникам с этими знаниями, вот мне эти хорды нигде не пригодились, далеко не всю геометрию можно направить в практическое русло.

Источник

Технологическая карта урока в 8 классе по теме «Свойства хорд»

Ищем педагогов в команду «Инфоурок»

Технологическая карта урока

Цели урока (занятия) как планируемые результаты обучения, планируемый уровень достижения целей:

Вид планируемых учебных действий

Планируемый уровень достижения результатов обучения

Показывают знания по теме « Окружность» : элементы окружности, взаимное расположение прямых, вписанный и центральный углы.
Решают задачи разных уровней на нахождение

2 уровень (воспроизведение)

2 уровень (воспроизведение с помощью учителя)

3 уровень ( самостоятельное выполнение)

2 уровень (воспроизведение с помощью учителя)

3 уровень ( самостоятельное выполнение)

Самостоятельное выделение и формулирование познавательной цели;
Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности ; моделирование; анализ и синтез информации

3 уровень ( самостоятельное выполнение)

Планирование учебного сотрудничества с учителем и сверстниками – определение целей, функций участников, способов взаимодействия; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, принятие решения и его реализация;

2 уровень (воспроизведение с помощью учителя)

Способность к самооценке на основе критерия успешности учебной деятельности, мотивация (смыслообразование) учебной деятельности, личностное самоопределение.

3 уровень ( самостоятельное ывыполнение)

Формы учебного взаимодействия

Формируемые УУД и предметные действия

Создать благоприятный психологический настрой на работу

Обеспечение мотивации учения детьми, принятие ими целей урока

2.Настраивает учащихся для работы на уроке

3.Объявляет, что на уроке мы будем продолжать изучать понятия, связанные с темой «Окружность»

4.Ставит перед учащимися вопрос: «Зачем им знания по теме окружность? Пригодятся ли они им в жизни?»

5. Предлагает рассмотреть практический пример из романа Генри Лонгфелло , американского писателя, поэта-романтика, жившего в 19в. Лонгфелло был еще и атематиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в своем романе “Каванг”, позволяют запечатлеть на всю жизнь некоторые теоремы и их применение. Читаем в романе задачу… Как вы думаете какое отношение к нашей теме имеет эта задача?

6.Организует постановку проблемы (Определить глубину озера), исходя из условия задачи, выдвижение гипотезы, цели работы, планирование исследовательской работы.

2. Отвечают на поставленный вопрос о значимости понятий окружности в жизни.

3. Выдвигают гипотезу о том , что по условию задачи Лонгфелло можно построить математическую модель озера (окружность), где поверхность воды и стебель лилии будут пересекающимися хордами, отрезок которой необходимо найти, для того чтобы определить глубину озера.

4. Планируют исследовательскую деятельность:

—повторить уже изученные понятия;

-изучить свойства хорд, выборочно доказать, имеющиеся свойства;

-закрепить свойства на простейших задачах

-познакомить одноклассников с полученными знаниями;

-применить необходимые свойства для решения проблемной задачи.

Познавательные:самостоятельное выделение и формулирование познавательной цели

Коммуникативные:планирование учебного сотрудничества с учителем и сверстниками

Регулятивные: целеполагание, саморегуляция

Актуализация и фиксирование индивидуального затруднения в пробном учебном действии.

Актуализация опорных знаний и способов действий

1. Теорети-ческий тест по теме «Окружность»

Самопроверка по образцу

1.Проводит тест по изученным терминам темы, в котором необходимо вставить пропущенные слова в предложения.

2. Проводит фронтальный опрос по тестовой работе, организуя индивидуальную самопроверку.

3. Знакомит с критериями оценивания теста. Проводит рефлексию результатов.

1. Отвечают на вопросы теста

2. Зачитывают ответы

3. Самостоятельно оценивают результаты теста, согласно озвученным.

4.Проводят рефлексию своих знаний по теме «Окружность»

Предметные:повторение понятий элементов окружности, свойств касательных вписанных и центральных углов

Познавательные:моделирование, анализ, синтез

Коммуникативные:постановка вопросов, учебное сотрудничество

Выявление практической значимости изучаемого материала. Организация исследовательской деятельности при решении проблемной

1. Постановка проблемной вопроса

2.Планирование исследовательской деятельности

3. Решение проблемной ситуации

5. Проводит исследовательскую работу:

-Делит учащихся на 3 группы, задаёт задание, исходя из плана исследовательской деятельности;

-Консультирует учащихся по проблемным вопроса в группах;

-Организует публичное выступление участников групп;

6. Проводит заключительную работу по решению проблемной задачи.

1. Работают в группах

1 группа – доказательство свойств 1,3,5

2 группа – доказательство свойств 2, 4, 6

3 группа – решение задач 1, 3, 5

2. Выступают по изученным вопросам перед классом

3. Заполняют графы таблицы

4. Решают проблемную задачу на основе изученных знаний.

4. Делают вывод по изученной проблеме

Предметные:повторение свойств площадей, т.Пифагора, применение на задачах среднего уровня сложности

Познавательные:постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности

Коммуникативные: умение с достаточной полнотой выражать свои мысли, принятие решения и его реализация

Регулятивные:планирование, контроль, оценка

Дать качественную оценку работы класса и отдельных обучаемых

Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе

1.Дифференцуруемая домашняя работа

2. Самооценка результатов

1.Задаёт и объясняет выполнение дифференцированного домашнего задания :

-на оценки «4» или «5» доказать и выучить оставшиеся свойства и решить соответствующие задачи.

-на оценку «3» выучить свойства решить оставшиеся задачи.

2.Подводит итоги урока, качественную оценку результатов

3. Проводит рефлексию, предлагая нарисовать смайлик настроения из элементов окружности

1.Записывают домашнее задание

2. Выставляют оценку, исходя из среднего балла по результатам теста и исследовательской работы

3. Рисуют « Смайлик настроения» из геометрических фигур, изученных в этой теме.

Предметные: разбор домашнего задания

Познавательные:рефлексия способов и условий действий, контроль и оценка процесса и результатов действий

Источник

Конспект урока тип хордовые

Ищем педагогов в команду «Инфоурок»

Конспект урока биологии в 7 классе «Тип Хордовые. Подтип Бесчерепные и Черепные, или Позвоночные»

Тема Тип Хордовые. Подтип Бесчерепные и Черепные или Позвоночные

Цели урока: сформировать представление о типе Хордовые. Дать определение понятий хорда, череп, позвоночник, бесчерепные, ланцетники, черепные. Выделить существенные признаки особенности строения хордовых животных. Научиться классифицировать и различать животных подтипов Бесчерепные и Черепные.

Познавательные : выделять объекты и процессфы с точки зрения целого и частей; строить рассуждения, включающие установление причинно-следственных связей.

Регулятивные : определять цель урока и ставить задачи, необходимые для ее достижения; планировать свою деятельность и делать выводы по результатам работы.

Коммуникативные : работая в составе творческих групп, аргументировать свою точку зрения.

Тип урока: урок открытия нового знания.

V. Организация начала занятий. Приветствие, фиксация отсутствующих; проверка подготовленности классного помещения; организация внимания школьников; раскрытие общей цели урока и плана его проведения.

VI. Этап проверки выполнения домашнего задания. 1. Проверить заполнение таблицы.

2. Фронтальный опрос :

Какие особенности жизни перепончатокрылых не свойственны другим отрядам?

Каково значение пчел в природе и жизни человека?

Как пчелы узнают дорогу к местам с обилием цветущих растений медоносов?

Муравьи. Чем они интересны?

VII. Подготовка к основному этапу занятия. Формулировка целей урока вместе с учащимися

V. Первичное понимание усвоение материала.

— Почему ланцетник – это низшее хордовое животное?

— Почему ланцетник относится к подтипу Бесчерепные?

— Как приспособлен ланцетник к подземно –донному образу жизни?

— Какое значение имеет ланцетник в природе и жизни человека?

— Какие ещё животные относятся к низшим хордовым

VI. Закрепление знаний и способов действий.

№ 1 Что общего в значении хорды у хордовых животных и хитинового панциря у членистоногих?

(выполняют роль скелета)

№ 2 В чём отличие скелета высших и низших хордовых?

(в отличие от низших, у высших хордовых хорда есть только на зародышевой стадии, а затем она заменяется хрящевым или костным позвоночником)

№ 3 Каково происхождение головного мозга у высших хордовых?

(нервная трубка в передней части расширяется и превращается в головной мозг)

№ 4 Можно ли встретить ланцетника в Балтийском море?

(нет, так как они обитают в тёплых морях)

№ 5 Докажите верность утверждения : «Круглоротые – связующее эволюционное звено между бесчерепными и рыбами, которое природа сохранила до наших дней».

(как и ланцетник круглоротые имеют хорду в течении всей жизни, но по общему строению они ближе к рыбам, так как имеют череп, головной мозг, сердце, жабры)

VII. Этап рефлексии учебной деятельности. Слайд 11 Составление синквейна (коллективная работа)

Укрепляет, поддерживает, защищает

В процессе эволюции превращается в позвоночник

VIII. Информация о дом задании. Слайд 12 параграф 20 читать, пересказывать, знать определения. Стр 96 №4 устно. Зарисовать внутреннее строение ланцетника, подписать органы, пример в интернете.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

Курс профессиональной переподготовки

Биология: теория и методика преподавания в образовательной организации

Конспект урока биологии в 7 классе «Тип Хордовые. Подтип Бесчерепные и Черепные, или Позвоночные»

Тема Тип Хордовые. Подтип Бесчерепные и Черепные или Позвоночные

Цели урока: сформировать представление о типе Хордовые. Дать определение понятий хорда, череп, позвоночник, бесчерепные, ланцетники, черепные. Выделить существенные признаки особенности строения хордовых животных. Научиться классифицировать и различать животных подтипов Бесчерепные и Черепные.

Познавательные: выделять объекты и процессфы с точки зрения целого и частей; строить рассуждения, включающие установление причинно-следственных связей.

Регулятивные: определять цель урока и ставить задачи, необходимые для ее достижения; планировать свою деятельность и делать выводы по результатам работы.

Коммуникативные: работая в составе творческих групп, аргументировать свою точку зрения.

Тип урока: урок открытия нового знания.

Оборудование: таблицы «Ланцетник», «Миноги». Презентация «Тип Хордовые»

Этапы урока:

V. Организация начала занятий. Приветствие, фиксация отсутствующих; проверка подготовленности классного помещения; организация внимания школьников; раскрытие общей цели урока и плана его проведения.

VI. Этап проверки выполнения домашнего задания. 1. Проверить заполнение таблицы.

2. Фронтальный опрос:

Какие особенности жизни перепончатокрылых не свойственны другим отрядам?

Каково значение пчел в природе и жизни человека?

Как пчелы узнают дорогу к местам с обилием цветущих растений медоносов?

Муравьи. Чем они интересны?

VII. Подготовка к основному этапу занятия. Формулировка целей урока вместе с учащимися

V. Первичное понимание усвоение материала.

— Почему ланцетник – это низшее хордовое животное?

— Почему ланцетник относится к подтипу Бесчерепные?

— Как приспособлен ланцетник к подземно –донному образу жизни?

— Какое значение имеет ланцетник в природе и жизни человека?

— Какие ещё животные относятся к низшим хордовым

VI. Закрепление знаний и способов действий.

№1 Что общего в значении хорды у хордовых животных и хитинового панциря у членистоногих?

(выполняют роль скелета)

№2 В чём отличие скелета высших и низших хордовых?

(в отличие от низших, у высших хордовых хорда есть только на зародышевой стадии, а затем она заменяется хрящевым или костным позвоночником)

№3 Каково происхождение головного мозга у высших хордовых?

(нервная трубка в передней части расширяется и превращается в головной мозг)

№4 Можно ли встретить ланцетника в Балтийском море?

(нет, так как они обитают в тёплых морях)

№ 5 Докажите верность утверждения: «Круглоротые – связующее эволюционное звено между бесчерепными и рыбами, которое природа сохранила до наших дней».

(как и ланцетник круглоротые имеют хорду в течении всей жизни, но по общему строению они ближе к рыбам, так как имеют череп, головной мозг, сердце, жабры)

VII. Этап рефлексии учебной деятельности. Слайд 11 Составление синквейна (коллективная работа)

Хорда

Укрепляет, поддерживает, защищает

В процессе эволюции превращается в позвоночник

VIII. Информация о дом задании. Слайд 12 параграф 20 читать, пересказывать, знать определения. Стр 96 №4 устно. Зарисовать внутреннее строение ланцетника, подписать органы, пример в интернете.

Источник

Геометрия. 8 класс

Отрезок, соединяющий две точки окружности, называется ее хордой.
Свойства хорд окружности
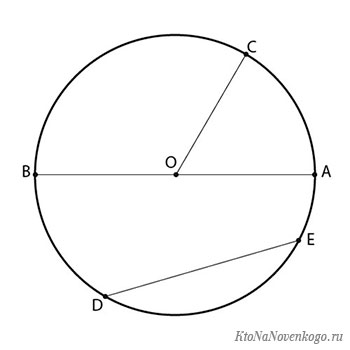
Теорема: Радиус, перпендикулярный к хорде, делит эту хорду пополам.

Дано: окружность с центром O, AB – хорда, OC ⊥ AB
Доказать: AM = MB
Доказательство:
Проведём радиусы OA и OВ.

Дано: окружность с центром O, AB – хорда, AM = MB
Доказать: OC ⊥ AB
Докажите самостоятельно.
Докажем еще одно свойство хорд окружности: Дуги, заключенные между равными хордами, равны.

Дано: окружность с центром O, AB и CD – хорды, AB = CD
Доказать: ∪AB = ∪CD
Доказательство:
Проведём радиусы ОА, ОВ, ОС и ОD
∆ AOB = ∆ COD (по трём сторонам: два радиуса и равные хорды), следовательно ∠COD = ∠BOA. Они являются центральными углами окружности. Значит, равны дуги, на которые они опираются, т.е. ∪AB = ∪CD
Самостоятельно докажите утверждение: Дуги, заключённые между параллельными хордами, равны.
Дано: окружность с центром O, AB и CD – хорды, AB || CD
Доказать: ∪AC = ∪DB

Теорема об отрезках пересекающихся дуг
Теорема: Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой.
Дано: окружность c центром O, AB и CD – хорды, M – точка пересечения хорд

Доказать: AM ∙ MB = CM ∙ MD.
Доказательство:
Рассмотрим треугольники ADM и BDM.

В этих треугольниках ∠ACM = ∠DBM как вписанные опирающиеся на одну и ту же дугу AD.
∠CMB = ∠DMA (вертикальные)
По первому признаку подобия треугольников
∆ ACM

∆ DBM, отсюда следует равенство отношений
AM/DM = CM/BM, следовательно
AM ∙ MB = CM ∙ MD
Утверждение доказано.
Найдите в справочниках другие свойства хорд, докажите их самостоятельно.
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.

Источник

В каком классе изучают хорды

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.

Часть плоскости, ограниченная окружностью называется кругом.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Хорда

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Теорема о касательной и секущей

Углы в окружности

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.

Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Свойства углов, связанных с окружностью

C = 2 R.

L = R .

S = R 2 .

Вписанные и описанные окружности

Окружность и треугольник

где S — площадь треугольника, а — полупериметр;

R = ,

R = ;

здесь a, b, c — стороны треугольника, — угол, лежащий против стороны a, S — площадь треугольника;

Окружность и четырехугольники

+ = + = 180°;

a + c = b + d ;

Касательная к окружности

1. Угол ACO равен 28°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол САО — прямой. Из треугольника АСО получим, что угол АОС равен 62 градуса. Величина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги АВ — тоже 62 градуса.

2. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.

3. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Проведем радиус ОВ в точку касания, а также радиус ОА. Угол ОВС равен 90°. Треугольник ВОА — равнобедренный. Нетрудно найти, что угол ОВА равен 44 градуса, и тогда угол СВА равен 46 градусов, то есть половине угловой величины дуги АВ.

Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

4. Через концы A, B дуги окружности в 62° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

Рассмотрите четырехугольник ОВСА. Сумма углов любого выпуклого четырехугольника равна 360°. Углы ОВА и ОВС и ОАС — прямые, угол ВОА равен 62°, значит, угол АСВ равен 28 градусов.

5. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.

Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника АВС складывается из периметров отсеченных треугольников.

Все эти задачи встречаются в Банке заданий ФИПИ под номером В6. А вот одна из сложных задач В3:

6. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.

Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку О — и проведите перпендикулярные сторонам радиусы в точки касания.

Соедините точку О с вершинами А, В, С, D, E. Получились треугольники АОВ, ВОС, СОD, DOE и ЕОА.
Очевидно, что площадь многоугольника S = S_АОВ + S_ВОС + S_СОD + S_DOE + S_ЕОА.
Как вы думаете, чему равны высоты всех этих треугольников и как, пользуясь этим, найти радиус окружности?

Источник