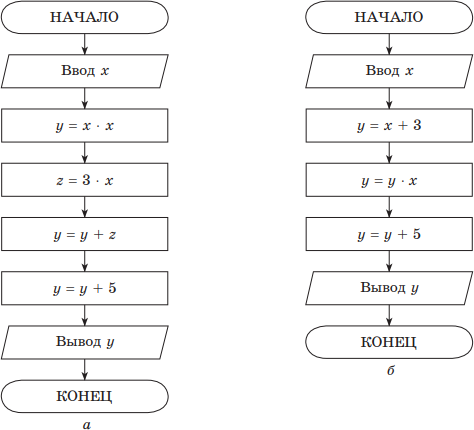
в каком алгоритме действие ведется последовательно
Тест по информатике Линейные алгоритмы. Алгоритмы с ветвлениями. Алгоритмы с повторениями для 6 класса
Тест по информатике Линейные алгоритмы. Алгоритмы с ветвлениями. Алгоритмы с повторениями для 6 класса с ответами. Тест включает в себя 2 варианта, в каждом варианте 10 заданий с выбором ответа.
1 вариант
1. Как называется алгоритм, в котором команды выполняются последовательно друг за другом?
1) линейный
2) с ветвлениями
3) с повторениями
4) все утверждения верны
2. Какой геометрической фигуры нет в блок-схеме линейного алгоритма?
1) овал
2) параллелограмм
3) ромб
4) прямоугольник
3. Какая фигура блок-схемы имеет два выхода?
1) овал
2) параллелограмм
3) ромб
4) прямоугольник
4. При выполнении линейного алгоритма каждый ли блок выполняется?
5. При выполнении алгоритма с ветвлением как выполняются действия? Выберите верное утверждение.
1) каждый блок выполняется один раз
2) не все блоки выполняются
3) некоторые блоки выполняются несколько раз
6. В каком типе алгоритма у блока есть два входа?
1) в линейном
2) с ветвлением
3) в циклическом
4) нет такого вида алгоритма
7. Что называется зацикливанием?
1) повторение последовательности действий несколько раз
2) организация цикла в алгоритме
3) отсутствие условия завершения цикла
4) все утверждения верны
8. Отличаются ли алгоритмы с повторениями от циклических?
9. Бывают ли циклические алгоритмы без ветвления?
10. Сколько фигур овал присутствуют в алгоритме?
1) 1
2) 2
3) 3
4) произвольное число раз
2 вариант
1. Как выполняются команды в линейном алгоритме?
1) последовательно друг за другом
2) в зависимости от выполнения условия одна группа команд или другая
3) группа команд повторяется несколько раз
4) все утверждения верны
2. Какая геометрическая фигура характеризует блок-схему алгоритма с ветвлением?
1) овал
2) параллелограмм
3) ромб
4) прямоугольник
3. Сколько выходов имеет фигура овал?
1) 1 или 2
2) всегда 1
3) 1 или 0
4) все утверждения не верны
4. Выберите верное утверждение. При выполнении линейного алгоритма как выполняются действия?
1) все блоки выполняются один раз
2) некоторая группа блоков не выполняется
3) некоторые блоки выполняются несколько раз
5. При выполнении алгоритма с ветвлением каждый ли блок выполняется?
6. В каком типе алгоритма часть действий повторяется определённое количество раз?
1) линейный
2) с ветвлением
3) циклический
4) все утверждения верны
7. Какой ситуации нельзя допустить в циклическом алгоритме?
1) повторения последовательности действий несколько раз
2) организации цикла в алгоритме
3) зацикливания
4) все утверждения верны
8. Может ли быть в одном алгоритме несколько ветвлений?
9. Какая роль ветвления в циклическом алгоритме?
1) ветвление не связано с циклом
2) проверяет условие повторения или выхода из цикла
10. Какой алгоритм имеет блок с двумя входами?
1) линейный
2) с ветвлением
3) циклический
4) все утверждения верны
Ответы на тест по информатике Линейные алгоритмы. Алгоритмы с ветвлениями. Алгоритмы с повторениями для 6 класса
1 вариант
1-1
2-3
3-3
4-1
5-2
6-3
7-3
8-2
9-2
10-2
2 вариант
1-1
2-3
3-3
4-1
5-2
6-3
7-3
8-1
9-2
10-3
Виды алгоритмов и типы их схем
В этой статье будут рассмотрены основные виды алгоритмов, а также схематические блоки, которые используются при их описании. Кроме получения информации о видах блоков алгоритмов, читатель узнает о наиболее популярных методах описания алгоритмических последовательностей. Будут приведены соответствующие примеры с пояснениями.
Блок-схема
Алгоритмы бывают разные, но прежде чем приступить к рассмотрению их видов, следует рассказать об основном способе визуализации алгоритмической последовательности — созданию блок-схемы. Такие схемы состоят из соответствующих функциональных блоков, которые связаны между собой. Каждый блок отвечает за выполнение какого-нибудь действия. Для каждого типа действия определён конкретный блок, представляющий собой геометрическую фигуру.
Существует и очередность выполнения действий — она определяется линиями, которые соединяют блоки. По умолчанию используемые в схеме блоки соединяются слева направо и сверху вниз. В случае другой последовательности выполнения, блоки соединяются направленными линиями (речь идёт о линиях, оснащённых стрелками).
Типы и назначение блоков алгоритма можно посмотреть в таблице ниже:
Теперь рассматривать виды алгоритмов будет гораздо понятнее.
Виды алгоритмов
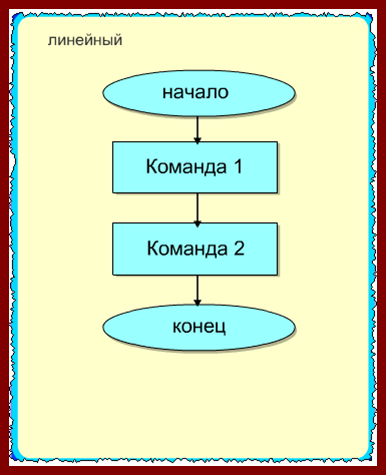
Алгоритмы бывают: — линейные – подразумевается последовательное выполнения операций (команд, указаний), то есть выполнение действий происходит друг за другом. Вот, как это выглядит на схеме с блоками:
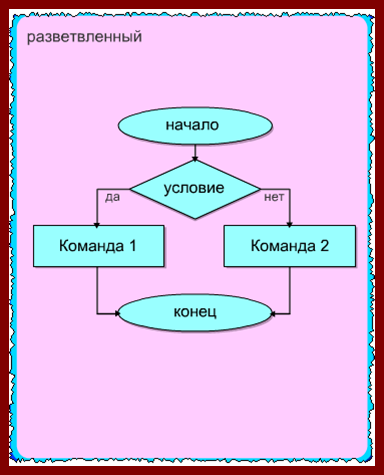
— разветвляющиеся – характеризуются выполнением хотя бы одной операции по проверке условия, в результате чего осуществляется переход действия на какой-нибудь другой из возможных вариантов решения. Смотрим схему:
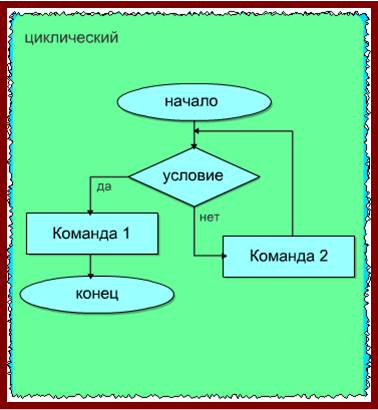
— циклические – данным алгоритмом предусмотрено многократное повторение определенной последовательности действий (речь идёт об одинаковых операциях). Здесь число повторений будет обусловлено либо условием задачи, либо исходными данными.
Также стоит добавить, что любая алгоритмическая конструкция способна включать в себя какую-нибудь другую конструкцию того либо иного вида, то есть алгоритмы бывают вложенными.
Способы описания алгоритмов
О блок-схеме, как об основном способе представления алгоритмов, мы уже поговорили. Но кроме блоков, есть и другие методы:
Алгоритм, содержащий цикл и ветвление
Теория к заданию 20 из ЕГЭ по информатике
Алгоритмизация и программирование
Алгоритмы, виды алгоритмов, описание алгоритмов. Формальное исполнение алгоритмов
Термин «алгоритм», впервые употребленный в современном значении. Лейбницем (1646–1716), является латинизированной формой имени великого персидского математика Мухаммеда бен Муссы аль-Хорезми (ок. 783 – ок. 850). Его книга «Об индийском счете» в XII в. была переведена на латинский язык и пользовалась широкой популярностью не одно столетие. Имя автора европейцы произносили как Алгоритми (Algorithmi), и со временем так стали называть в Европе всю систему десятичной арифметики.
Научное определение алгоритма дал А. Чёрч в 1930 году. В наше время понятие алгоритма является одним из основополагающих понятий вычислительной математики и информатики.
Алгоритм — это точное и полное описание последовательности действий над заданными объектами, позволяющее получить конечный результат.
Можно сказать, что алгоритм решения какой-либо задачи — это последовательность шагов реализации (или нахождения) этого решения, а процесс построения алгоритма (алгоритмизация) — разложение задачи на элементарные действия или операции.
Область математики, известная как теория алгоритмов, посвящена исследованию свойств, способов записи, области применения различных алгоритмов, а также созданию новых алгоритмов. Теория алгоритмов находит широкое применение в различных областях деятельности человека — в технике, производстве, медицине, образовании и т. д. Появление компьютера позволило решать чрезвычайно сложные, трудоемкие задачи.
Определение алгоритма для применения в области информатики нуждается в некотором уточнении. Во-первых, решение задач в информатике всегда связано с преобразованием информации, а значит, исходными данными и результатом работы алгоритма должна быть информация. Это может быть представлено в виде схемы.
Во-вторых, алгоритмы в информатике предназначены для реализации в виде компьютерных программ или для создания некоторой компьютерной технологии. Для выполнения алгоритма требуется конечный объем оперативной памяти и конечное время.
Основные требования, предъявляемые к алгоритмам:
Дискретность (прерывность): алгоритм должен представлять решение задачи в виде последовательности простых (или ранее определенных) этапов (шагов). Каждый шаг алгоритма формулируется в виде инструкций (команд).
Определенность (детерминированность; лат. determinate — определенность, точность): шаги (операции) алгоритма должны допускать однозначную трактовку и быть понятными для исполнителя алгоритма. Это свойство указывает на то, что любое действие в алгоритме должно быть строго определено и описано для каждого случая.
Массовость: алгоритм должен давать решение не только для конкретного набора значений, а для целого класса задач, который определяется диапазоном возможных исходных данных (область применимости алгоритма). Свойство массовости подразумевает использование переменных в качестве исходных данных алгоритма.
Результативность: алгоритм должен давать конкретный результат, т. е. должны быть рассмотрены все возможные ситуации и для каждой из них получен результат. Под результатом может пониматься и сообщение о том, что задача решения не имеет.
Конечность: количество шагов алгоритма должно быть конечным.
Эффективность: количество шагов и сами шаги алгоритма должны быть такими, чтобы решение могло быть найдено за конечное и, более того, приемлемое время.
Для оценки и сравнения алгоритмов существует много критериев. Чаще всего анализ алгоритма (или, как говорят, анализ сложности алгоритма) состоит в оценке временных затрат на решение задачи в зависимости от объема исходных данных. Используются также термины «временная сложность», «трудоемкость» алгоритма. Фактически эта оценка сводится к подсчету количества основных операций в алгоритме, поскольку каждая из них выполняется за заранее известное конечное время. Кроме временной сложности, должна оцениваться также емкостная сложность, т. е. увеличение затрат памяти в зависимости от размера исходных данных. Оценка сложности дает количественный критерий для сравнения алгоритмов, предназначенных для решения одной и той же задачи. Оптимальным (наилучшим) считается алгоритм, который невозможно значительно улучшить в плане временных и емкостных затрат.
Анализом сложности алгоритмов, исследованием классов задач, решаемых с помощью алгоритмов той или иной сложности, и многими другими теоретическими вопросами занимается специальная область информатики.
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов.
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур:
Для описания алгоритмов наиболее распространены следующие методы (языки):
Обычный язык. Изложение алгоритма ведется на обычном языке с разделением на последовательные шаги.
Блок-схемы. Графическое изображение алгоритма с помощью специальных значков-блоков.
Формальные алгоритмические языки (языки программирования). При записи алгоритмов используют строго определенный набор символов и составленных из них специальных зарезервированных слов. Имеют строгие правила построения языковых конструкций.
Псевдокод. Синтез алгоритмического и обычного языков. Элементы некоторого базового алгоритмического языка используются для строгой записи базовых структур алгоритма.
Словесный способ (запись на обычном языке) не имеет широкого распространения, т. к. таких описаний есть ряд недостатков:
Графический способ представления информации является более наглядным и компактным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление алгоритма называется блок-схемой. Определенному типу действия (ввод/вывод данных, проверка условия, вычисление выражения, начало и конец алгоритма и т. п.) соответствует определенная геометрическая фигура — блочный символ. Блоки соединяются между собой линиями переходов, которые определяют очередность выполнения действий.
| Название символа | Графическое изображение | Комментарии |
| Пуск/Останов (блоки начала и конца алгоритма) |  | Указание на начало или конец алгоритма |
| Ввод/Вывод данных (блоки ввода, вывода |  | Организация ввода/вывода в общем виде |
| Процесс (операторные блоки) |  | Выполнение вычислительного действия или последовательности действий (можно объединять в один блок), которые изменяют значение, форму представления или размещение данных |
| Условие (условный блок) | 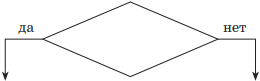 | Выбор направления выполнения алгоритма. Если условие, записанное внутри ромба, выполняется, то управление передается по стрелке «да», в противном случае — по стрелке «нет». Таким образом, реализуется процесс изменения последовательности вычислений в зависимости от выполнения условия |
| Начало цикла с параметром |  | Используется для организации циклических конструкций с известным количеством итераций (повторений) и известным шагом изменения параметра цикла. Внутри блока для параметра цикла указываются через запятую его начальное значение, конечное значение и шаг изменения. Цикл, для которого неизвестно количество повторений, записывается с помощью условного и операторных блоков |
| Предопределенный процесс |  | Используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращения к библиотечным подпрограммам |
| Печать сообщений (документ) |  | Вывод результатов на печать |
При составлении блок-схемы необходимо проверять выполнение следующих условий:
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. В псевдокоде не приняты строгие синтаксические правила для записи команд, что отличает формальные языки программирования. Однако в псевдокоде есть некоторые конструкции, которые присущи формальным языкам, что облегчает переход от записи алгоритма на псевдокоде к записи алгоритма на языке программирования. Псевдокоды бывают разные. Рассмотрим учебный (школьный) алгоритмический язык АЯ.
Алфавит учебного алгоритмического языка является открытым. В него могут быть введены любые понятные всем символы: русские и латинские буквы, знаки математических операций, знаки отношений, специальные знаки и т. д. Кроме алфавита, в алгоритмической нотации определяются служебные слова, которые являются неделимыми. Служебные слова обычно выделяются жирным шрифтом или подчеркиванием. К служебным словам относятся:
| алг — заголовок алгоритма | нц — начало цикла | знач |
| нач — начало алгоритма | кц — конец цикла | и |
| кон — конец алгоритма | дано | или |
| арг — аргумент | надо | не |
| рез — результат | если | да |
| цел — целый | то | нет |
| сим — символьный | иначе | при |
| лит — литерный | всё | выбор |
| лог — логический | пока | утв |
| вещ — вещественный | для | ввод |
| таб — таблица | от | вывод |
| длин — длина | до |
Общий вид записи алгоритма на псевдокоде:
алг — название алгоритма (аргументы и результаты)
дано — условие применимости алгоритма
надо — цель выполнения алгоритма
нач — описание промежуточных величин
последовательность команд (тело алгоритма)
Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон, — телом алгоритма (исполняемой частью алгоритма).
В предложении алг после названия алгоритма в круглых скобках указываются характеристики (арг, рез) и тип значения (цел, вещ, сим, лит или лог) всех входных (аргументы) и выходных (результаты) переменных. При описании массивов (таблиц) используется служебное слово таб, дополненное именем массива и граничными парами по каждому индексу элементов массива.
Команды учебного языка:
1. Оператор присваивания, который обозначается «:=» и служит для вычисления выражений, стоящих справа, и присваивания их значений переменным, указанным в левой части. Например, если переменная а имела значение 5, то после выполнения оператора присваивания а := а + 1, значение переменной а изменится на 6.
2. Операторы ввода/вывода:
ввод (список имен переменных)
вывод (список вывода)
Список вывода может содержать комментарии, которые заключаются в кавычки.
3. Оператор ветвления (с использованием команды если. то… иначе…всё; выбор);
4. Операторы цикла (с использованием команд для, пока, до).
Запись алгоритма на псевдокоде:
Здесь в предложениях дано и надо после знака «|» записаны комментарии. Комментарии можно помещать в конце любой строки, они существенно облегчают понимание алгоритма.
При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается произвольное изображение команд. Вместе с тем такая запись позволяет понять человеку суть дела и исполнить алгоритм. Однако алгоритм, предназначенный для исполнения на компьютере, должен быть записан на строго формализованном языке. Такой язык называется языком программирования, а запись алгоритма на этом языке — компьютерной программой.
Для решения одной и той же задачи можно предложить несколько алгоритмов. Алгоритмы составляются с ориентацией на определенного исполнителя алгоритма. У каждого исполнителя имеется свой конечный набор команд, которые для него понятны и исполняемы. Этот набор называется системой команд исполнителя. Пользуясь системой команд, исполнитель может выполнить алгоритм формально, не вникая в содержание поставленной задачи. От исполнителя требуется только строгое выполнение последовательности действий, предусмотренной алгоритмом. Таким образом, в общем случае алгоритм претерпевает изменения по стадиям:
Примеры решения задач
Пример 1. Исполнитель Утроитель может выполнить только две команды, которым присвоены номера:
Первая команда уменьшает число на 1, вторая — увеличивает его втрое.
Написать набор команд (не более пяти) получения из числа 3 числа 16. В ответе указать только номера команд.
Пример 2. Имеется Исполнитель алгоритма, который может передвигаться по числовой оси.
Система команд Исполнителя алгоритма:
1. «Вперед N» (Исполнитель алгоритма делает шаг вперед на N единиц).
2. «Назад M» (Исполнитель алгоритма делает шаг назад на M единиц).
Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было. Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?
1. Найдем, сколько было команд «Вперед», а сколько «Назад». Учитывая, что общее количество команд равно 50 и что команд «Назад» на 12 больше, чем команд «Вперед». Получим уравнение: x + (x + 12) = 50, где x — количество команд «Вперед». Тогда общее количество команд «Вперед»: x = 19, а количество команд «Назад»: 19 + 12 = 31.
2. Будем вести отсчет от начала числовой оси. Выполнив 19 раз команду «Вперед 3», Исполнитель алгоритма оказался бы на отметке числовой оси 57 (19 * 3 = 57). После выполнения 31 раз команды «Назад 2» (31 * 2 = 62) он оказался бы на отметке –5 (57 – 62 = –5).
3. Все эти команды можно заменить одной — «Назад 5».
Ответ: команда«Назад 5».
Пример 3. Черепашка является исполнителем для создания графических объектов на рабочем поле. При движении Черепашка оставляет след в виде линии. Черепашка может исполнять следующие команды:
| Название команды | Параметр | Действия исполнителя |
| вп | Число шагов | Продвигается в направлении головы на указанное число шагов |
| нд | Число шагов | Продвигается в направлении, противоположном направлению головы на указанное число шагов |
| пр | Число градусов | Поворачивается направо относительно направления, заданного головой черепашки |
| лв | Число градусов | Поворачивается налево относительно направления, заданного головой черепашки |
Для записи повторяющихся действий (цикла) используется команда Повтори. В этой команде два параметра: первый задает количество повторений (итераций), а второй — список команд которые должны повторяться (тело цикла); список заключается в квадратные скобки.
Записать для исполнителя Черепашка алгоритмы:
а) построения квадрата со стороной 100;
б) построения правильного шестиугольника со стороной 50.
в) построения изображения цифры 4, если голова Черепашки смотрит на север.
Ответ: а) Повтори 4 [вп 100 пр 90]; б) Повтори 6 [вп 50 пр 360/6]; в) вп 100; повтори [лв 135 вп 50].
Пример 4. Два игрока играют в следующую игру (это вариант восточной игры). Перед ними лежат три кучки камней, в первой из которых 2, во второй — 3, в третьей — 4 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в одной из кучек, или добавляет по два камня в каждую из них. Выигрывает игрок, после хода которого либо в одной из кучек становится не менее 15 камней, либо общее число камней в трех кучках становится не менее 25. Кто выиграет при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ следует обосновать.
Решение. Удобнее всего составить таблицу возможных ходов обоих игроков. Заметим, что в каждом случае возможны всего четыре варианта хода. В таблице курсивом выделены случаи, которые сразу же приносят поражение игроку, делающему этот ход (например, когда камней в какой-либо кучке становится больше или равно 8, другой игрок непременно выигрывает следующим ходом, удваивая количество камней в этой кучке). Из таблицы видно, что при безошибочной игре обоих игроков первый всегда выиграет, если первым ходом сделает 4, 5, 6. У второго игрока в этом случае все ходы проигрышные.
| 1-й ход | 2-й ход | |||
| Начало | 1-й игрок | 2-й игрок | 1-й игрок | 2-й игрок |
| 2,3,4 | 4,3,4 | 8,3,4 | выигрыш | |
| 4,6,4 | 8,6,4 | выигрыш | ||
| 4,12,4 | выигрыш | |||
| 4,6,8 | выигрыш | |||
| 6,8,6 | выигрыш | |||
| 4,3,8 | выигрыш | |||
| 6,5,6 | 12,5,6 | выигрыш | ||
| 6,10,6 | выигрыш | |||
| 6,5,12 | выигрыш | |||
| 8,7,8 | выигрыш | |||
| 2,6,4 | 4,6,4 | 8,6,4 | выигрыш | |
| 4,12,4 | выигрыш | |||
| 4,6,8 | выигрыш | |||
| 6,8,6 | выигрыш | |||
| 2,12,4 | выигрыш | |||
| 2,6,8 | выигрыш | |||
| 4,8,6 | выигрыш | |||
| 2,3,8 | выигрыш | |||
| 4,5,6 | 8,5,6 | выигрыш | ||
| 4,10,6 | выигрыш | |||
| 4,5,12 | выигрыш | |||
| 6,7,8 | выигрыш | |||
Пример 5. Записано 7 строк, каждая из которых имеет свой номер. В нулевой строке после номера записана цифра 001. Каждая последующая строка содержит два повторения предыдущей строки и добавленной в конец большой буквы латинского алфавита (первая строка — A, вторая строка — B и т. д.). Ниже приведены первые три строкиєтой записи (в скобках указан номер строки):
Какой символ находится в последней строке на 250-м месте (считая слева направо)?
Примечание. Первые семь букв латинского алфавита: A, B, C, D, E, F, G.
Решение. Найдем длину каждой строки. Длина каждой следующей строки в два раза больше длины предыдущей плюс один символ, длина строк составит:
(6) 127*2+1=255 символов.
Так как задано 7 строк, а нумерация начинается с нулевой строки, последняя строка имеет номер 6 и содержит 255 символов. Последний символ в строке — F. Предпоследний элемент — E, далее идут символы D, C, B, A, 1 (по правилу формирования строк). Таким образом, 250-й символ — это 1.
Пример 6. Имеется фрагмент алгоритма, записанный на учебном алгоритмическом языке:
нц для i от 7 до n – 1
Здесь переменные а, b, с — строкового типа; переменные n, i — целые.
В алгоритме используются следующие функции:
Длина(х) — возвращает количество символов в строке х. Имеет тип «целое».
Извлечь(х, i) — возвращает i-й символ слева в строке х. Имеет строковый тип.
Склеить(х, у) — возвращает строку, в которой находятся все символы строки х, а затем все символы строки у. Имеет строковый тип.
Какое значение примет переменная b после выполнения этого фрагмента алгоритма, если переменная а имела значение «ВОСКРЕСЕНЬЕ»?
Решение. Находим общее число символов в строке а, получим, что n = 11.
Выполняя команду b := Извлечь(а, k) при k = 2, получим, что b примет значение «О«.
В цикле последовательно, начиная с 7-го символа строки а и заканчивая предпоследним (n – 1), извлекаем символ из строки а и присоединяем к строке b.
В результате получим слово «ОСЕНЬ» (символы с номерами 2 + 7 + 8 + 9 + 10).
Пример 7. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который называется его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака», написанной в 1202 году. Он выглядит так:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.
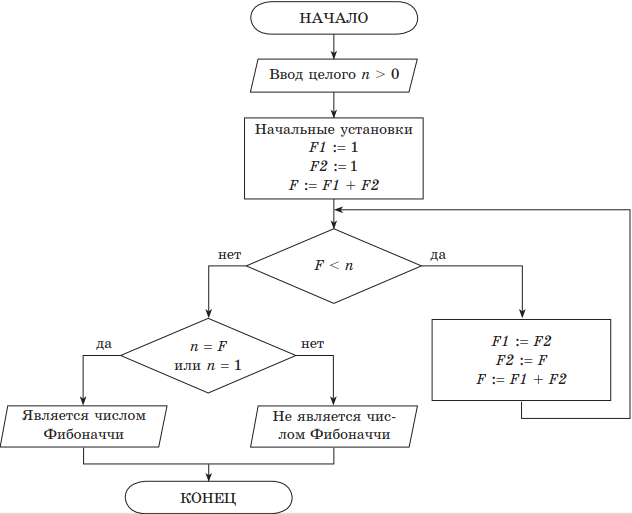
В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих. Составить словесный алгоритм и блок-схему проверки принадлежности введенного числа n ряду Фибоначчи.
Решение. Словесный алгоритм:
Приведенный словесный алгоритм в пункте 1, 2 содержит начальные установки, в пункте 3 — цикл с условием, а пункт 4 — это вывод результата работы алгоритма.
F — текущее число ряда Фибоначчи;
F1 и F2 — два предыдущих числа ряда Фибоначчи для числа F;
n — число, для которого требуется определить, является ли оно числом из ряда Фибоначчи.
Использование основных алгоритмических конструкций: следование, ветвление, цикл
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.
Базовая структура СЛЕДОВАНИЕ указывает на то, что управление передается последовательно от одного действия к другому.
| Учебный алгоритмический язык | Язык блок-схем |
| действие 1 действие 2 … действие n | 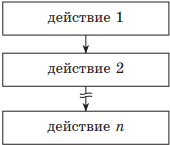 |
Использование исключительно этой структуры возможно лишь для достаточно простых задач, ход решения которых не меняется в зависимости от конкретных исходных данных и состоит в последовательном выполнении определенных операций.
В качестве примера рассмотрим решение простой задачи.
Пример. Найти y(x) = x2 + 3x + 5, используя только операции умножения и сложения.
Решение. На рис. приводятся два алгоритма, реализующие решение поставленной задачи.
Порядок вычисления y(x) в первом случае — обычный, а во втором — (x + 3) x + 5. Обе формулы эквивалентны, но в первом случае для вычисления необходимо 2 умножения, 2 сложения и 3 переменных (x, y, z), а во втором используются 1 умножение, 2 сложения и 2 переменные (x, y).
Приведенный пример показывает, что даже простые задачи могут решаться с помощью различных вариантов алгоритмов.
Обратите внимание, как в блоке следования используется оператор присваивания.
Операция присваивания — важнейшая операция во всех языках программирования. С помощью присваивания переменные получают новые значения: в левой части инструкции ставится идентификатор величины, а в правой части — выражение, значение которого можно определить.
В операторах присваивания используется либо привычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных правой части уже определены.
Базовая структура ВЕТВЛЕНИЕ (РАЗВИЛКА) используется в случае, когда выполнение программы может измениться в зависимости от результата проверки условия и пойти двумя разными (альтернативными) путями. Другими словами, условие является некоторым высказыванием (предикатом) и может быть истинным или ложным (принимать значение TRUE или FALSE). Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.
Различают две структуры этого типа — полную и неполную. В случае полной структуры, если условие выполняется (является истинным), вслед за ним выполняется действие 1, иначе — действие 2. В случае неполной структуры, если условие выполняется (является истинным), то вслед за ним выполняется действие 1, иначе ничего не происходит.
Важную роль в операторах ветвления играют содержащиеся в них условия. В простейшем случае условиями служат отношения между величинами. Условия с одним отношением называют простыми условными выражениями, или простыми условиями. В некоторых задачах необходимы более сложные условия, состоящие из нескольких простых, например условие А C) (возможна запись (Х C)). Объединение нескольких простых условий в одно образует составное условное выражение, или составное условие. Составные условия образуются с помощью логических операторов not (отрицание), and (логическое И), or (логическое ИЛИ), хоr (исключающее ИЛИ).
Структура ВЕТВЛЕНИЕ существует в четырех основных вариантах:
если — то (неполная структура);
если — то — иначе (полная структура);