что такое вектор в жизни

Векторная психология. За и против

Сегодня я хотел бы написать о таком явлении, как векторная психология. Те, кто с ним знаком, думаю искали разного рода информацию и знают, что выдает поиск при соответствующем запросе и кого именно он чаще всего выдает. Мнения обычно противоположные и сейчас я бы хотел высказать свое относительно данной темы.

Сравнительно недавно я познакомился с таким понятием, как векторная психология. И в свойственной для себя манере тут же окунулся в это по самые ушки, просмотрев порядка 50 часов видео, прочитав несколько книг и энное количество статей, а так же подписавшись на телеграмм-канал одного из тех, кто продвигает данное направление в массы. За что ему в принципе спасибо. И так, что же такое вектор, зачем он нужен и почему вдруг появились люди, которые активно толкают все это на просторах интернета.

В 1908 году ни кто-нибудь, а сам Зигмунд Фрейд опубликовал статью «Характер и анальная эротика», ставшую началом психоаналитического учения о характерах. Кратко описав в этой статье психологические особенности людей с высокой чувствительностью ануса, Фрейд поставил задачу своим последователям:

«Следовало бы обратить внимание и на другие черты характера и выяснить, нет ли и в иных случаях связи с определёнными эрогенными зонами»

Не заставив себя долга ждать, вскоре появляются следующие работы: Эрнест Джонс: «Об анально-эротических чертах характера», Ганс фон Халлинберг: «Анальная эротика, любовь к страху и упрямство» и Исидор Задгер: «Уретральная эротика» и «Эротика кожи и мышечной системы».

В конце же XX века психолог В. Толкачев по стопам исследований своего учителя, академика В. Ганзена создал и описал целостную систему из 8 векторов. В чем же ее суть?

А сейчас объясню, с чем я не согласен. Какими бы характеристиками мы не обладали с самого рождения, все таки у нас есть душа, родители, окружение, какие-то случаи и происшествия в жизни, дополнительные особенности и предрасположенности (а упор только лишь в векторную психологию ограничивает нас, как существ развитых, подгоняя всех под одну гребенку). Все вместе они и формируют в нас будущего взрослого. Нынешние же продвиженцы темы векторов основываются на следующем: воспитание порождает в нас детскую обиду на родителей и сбивает с курса заложенной векторной настройки (от незнания последними, что мы вообще-то все разные). Как итог-через эту самую обиду мы в конечном счете и видим весь мир. И контактируем с ним через нее же. Осознав и прожив эту обиду, а в дальнейшем наполнив свои доминирующие вектора (про которые мы естественно узнаем на тренинге) тем, что является их сильными составляющими, мы наконец обретем счастье, здоровье и материальное благополучие. В чем, собственно, подвох? 1. Ни один тренинг, будь он хоть двухнедельный, не в состоянии изменить устоявшуюся психику взрослого человека за столь короткое время. Это просто невозможно! А вот навредить может 2. Их теории ставят в один ряд тех, кого один раз последним забрали из сада, в следствии чего он решил, что его видимо не любят (это его обида) и тех, кого подвергали с раннего детства сексуальному насилию в секте. Методы вывода человека на новый уровень одинаковые (ну это же тренинг). На кого рассчитаны подобные методы? Правильно! На инфантильных личностей, живущих в поисках волшебной таблетки. Для чего они разрабатывают эти методы, если они не работают? Правильно! Тренинги стоят от четырехзначных до шестизначных сумм! Именно поэтому всем известная (известная тем, кто вникал в тему векторов) СВП Бурлана распиарина лучше, чем Оля Бузова, а мнения о ней всего два: не работает (те, кто видимо потратился) и, цитирую, «Есть только одна действующая векторная психология. И это СВП Юрия Бурлана!». Звучит как призыв сектанта (надеюсь авторам таких сообщений хотя бы платят). Поверьте, даже тренинги Тони Роббинса не имеют продолжительного эффекта и положительно работают только с уже подготовленной психикой. А это, на секундочку, лучший коуч в мире! 3. Люди, которые придумывают эти тренинги, не имеют никакого понятия о психике человека, у них нет соответствующего образования. Им неведомы механизмы работы в тех или иных случаях. Для них все люди-одинаковые. А уверенность в том, что то, что они придумали и проверили на себе, сработает на других, держится лишь на том, что оно и правда на них сработало. Несколько раз. Вот только создавали они это исходя из своих взглядов и ценностей. И со своим ярым желанием создать что-то работающее и приносящее прибыль.

Вывод: изучить вектора полезно, может даже нужно, но для того лишь, чтобы понять, что мы такие, какие есть. И другими нам не стать. Все. Отдавать по 100000 рубликов за тренинг, который полностью изменит Вашу жизнь? Ну конечно нет. Потому что тренинги на неподготовленную психику никакого, кроме кратковременного, влияния не окажут. Берегите свое время и деньги.

Источник

Обычно потому, что плохо осознаем свои истинные желания, руководствуясь при выборе дела своей жизни влиянием извне: модой, советами родителей и друзей или просто собственными иллюзиями.

Хорошо, если это произойдет как можно раньше, в детском возрасте. Сам ребенок, конечно же, не в состоянии определиться со своими желаниями, но помочь ему в этом могут родители. Имея знания по системно векторной психологии, уже с самого раннего возраста они увидят в нем проявление тех или иных векторов, то есть природно заданных способностей, которые впоследствии реализуются их видовой ролью в обществе.

Доминантные вектора

Верхние и нижние вектора

Что такое реализация?

Теперь, определившись со своими природными желаниями и выбрав стержень, стоит задуматься о том, что такое реализация. Чем мы руководствуемся при выборе работы? В настоящее время все чаще можно слышать такие варианты: величиной заработной платы, наличием социального пакета, удобством местоположения. А в целом, это можно выразить так: хочу взять от работы как можно больше, а отдать как можно меньше. И уже практически нигде не услышишь: хочу максимально реализовать свой потенциал на благо общества, хочу работать для людей. То есть при поиске работы мы изначально руководствуемся неправильным намерением. Вопрос должен ставиться так: «Что я могу дать обществу?»

— определиться со своим векторным набором;

— найти стержень в виде доминантного вектора, доминантного желания;

— найти правильное намерение в реализации на отдачу.

Источник

Применение векторов в повседневной жизни

С понятием вектора мы встречаемся чаще,чем сами подозреваем. В данной работе я постаралась максимально изучить, в каких же сферах мы взаимодействуем с ним.

Просмотр содержимого документа
«Применение векторов в повседневной жизни»

С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор. Далее, в процессе работы над данным проектом, я приведу ещё множество не менее интересных примеров векторов.

Вообще, я считаю, что математика – это интереснейшая наука, в познании которой нет границ. Я выбрала тему о векторах не случайно, меня очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, я думаю, что эта тема весьма актуальна. В психологии, биологии, экономике и многих других науках употребляют понятие «вектор». Подробнее об этом я расскажу позже.

Целями данного проекта являются приобретение навыков работы с векторами, умение видеть необычное в обычном, выработка внимательного отношения к окружающему миру.

История возникновения понятия вектор

Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.

Вектор относительно новое математическое понятие. Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат и термин «скаляр», «скалярное произведение», «векторное произведение». Почти одновременно с ним исследования в том же направлении, но с другой точки зрения вёл немецкий математик Герман Грассман (1809 – 1877). Англичанин Уильям Клиффорд (1845 – 1879) сумел объединить два подхода в рамках общей теории, включающий в себя и обычное векторное исчисление. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу.

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.

Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками. В соответствии с требованиями новой программы по математике и физике понятие вектора стало одним из ведущих понятий школьного курса математики.[2]

Векторы в математике

Вектором называется направленный отрезок, который имеет начало и конец.[1]

Вектор с началом в точке А и концом в точке В принято обозначать как АВ. Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними, например .

Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector, несущий). Действительно, каждый направленный отрезок однозначно определяет собой какой-то параллельный перенос плоскости или пространства: скажем, вектор АВ естественно определяет перенос, при котором точка А перейдет в точку В, также и обратно, параллельный перенос, при котором А переходит в В, определяет собой единственный направленный отрезок АВ.

Длиной вектора АВ называется длина отрезка АВ, её обычно обозначают АВ. Роль нуля среди векторов играет нулевой вектор, у которого начало и конец совпадают; ему, в отличие от других векторов, не приписывается никакого направления.

Два вектора называются коллинеарными, если они лежат на параллельных прямых, либо на одной прямой. Два вектора называются сонаправленными, если они коллинеарны и направлены в одну сторону, противоположно направленными, если коллинеарны и направлены в разные стороны.

Операции над векторами

Модулем вектора АВ называется число, равное длине отрезка АВ. Обозначается, как АВ. Через координаты вычисляется, как:

=+ +

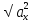
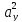
В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

)<\displaystyle <\vec >+<\vec >=(a_+b_,a_+b_,a_+b_)>

Для геометрического построения вектора суммы <\displaystyle <\vec >=<\vec >+<\vec >>c = используют различные правила (методы), однако они все дают одинаковый результат. Использование того или иного правила обосновывается решаемой задачей.

Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов <\displaystyle <\vec >> и <\displaystyle <\vec >> некоторой точки будет тем же, что применение сразу одного переноса <\displaystyle <\vec >+<\vec >>, соответствующего этому правилу. Для сложения двух векторов<\displaystyle <\vec >> и <\displaystyle <\vec >> по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

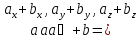
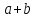
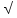
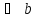
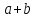
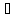
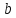
Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:

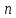
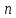
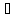
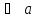
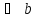
Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же <\displaystyle n>векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом <\displaystyle n>— го (то есть изображается направленным отрезком, замыкающим ломаную). Так же называется правилом ломаной.

Для сложения двух векторов <\displaystyle <\vec >> и <\displaystyle <\vec >> по правилу параллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.

Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:

‚ <\displaystyle <\vec >—<\vec >=(a_-b_,a_-b_,a_-b_)>

Для получения вектора разности <\displaystyle <\vec >=<\vec >—<\vec >> начала векторов соединяются и началом вектора <\displaystyle <\vec >> будет конец <\displaystyle <\vec >>, а концом — конец <\displaystyle <\vec >>. Если записать, используя точки векторов, то AC-AB=BC<\displaystyle <\overrightarrow >-<\overrightarrow >=<\overrightarrow >>.

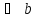
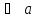
Умножение вектора на число

Скалярное произведение векторовСкалярное

Скалярным произведением называют число, которое получается при умножении вектора на вектор. Находится по формуле:

Скалярное произведение можно найти ещё через длину векторов и угол между ними.

Применение векторов в смежных науках Векторы в физике Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Векторы в литературе Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу сил равна нулю. А сила, как известно, векторная величина. Векторы в химии

Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца.

Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».

Все прямые химических реакций проходят через начало координат. Любую прямую в пространстве нетрудно выразить векторами, но поскольку прямая химической реакции проходит через начало системы координат, то можно принять, что вектор прямой химической реакции находится на самой прямой и называется радиус-вектором. Начало этого вектора совпадает с началом системы координат. Таким образом, можно сделать вывод: любая химическая реакция характеризуется положением ее вектора в пространстве. Векторы в биологии

Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы.

Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.

Векторы в экономике

Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора.

Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.

Векторы в психологии

На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов.

Векторы в повседневной жизни

Я обратила внимание, что векторы, помимо точных наук, встречаются мне каждый день. Так, например, во время прогулки в парке, я заметила, что ель, оказывается, можно рассматривать как пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора. А вывески с изображением вектора при посещении больших магазинов помогают нам быстро найти тот или иной отдел и сэкономить время.

Векторы в знаках дорожного движения

Каждый день, выходя из дома, мы становимся участниками дорожного движения в роли пешехода либо в роли водителя. В наше время практически каждая семья имеет машину, что, разумеется, не может не отразиться на безопасности всех участников дорожного движения. И, чтобы избежать казусов на дороге, стоит соблюдать все правила дорожного движения. Но не стоит забывать того, что в жизни всё взаимосвязано и, даже в простейших предписывающих знаках дорожного движения, мы видим указательные стрелки движения, в математике называемые – векторами. Эти стрелки (векторы) указывают нам направления движения, стороны движения, стороны объезда, и ещё многое другое. Всю эту информацию можно прочитать на знаках дорожного движения на обочинах дорог.

Базовое понятие «вектор», рассмотренное нами ещё на уроках математики в школе, является основой для изучения в разделах общей химии, общей биологии, физики и других наук. Я наблюдаю необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию в знаках дорожного движения.

Каждый человек постоянно сталкивается с векторами в повседневной жизни.

Векторы необходимы нам для изучения не только математики, но и других наук.

Источник