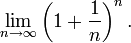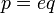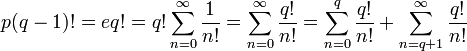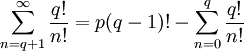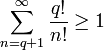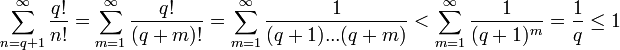что такое в математике inv

Решение систем линейных уравнений с помощью Python’s Numpy

Два или более линейных уравнения с одинаковым набором переменных называются системой линейных уравнений. Мы можем решить эти переменные в Python с помощью Numpy.

Библиотека Numpy может использоваться для выполнения различных математических/научных операций, таких как матричные кросс-и точечные произведения, поиск значений синуса и косинуса, преобразование Фурье и манипулирование формой и т. Д. Слово Numpy-это сокращенное обозначение “Числового питона”.

В этой статье вы увидите, как решить систему линейных уравнений с помощью библиотеки Numpy Python.

Что такое Система линейных уравнений?

В математике система линейных уравнений (или линейная система) представляет собой совокупность двух или более линейных уравнений, включающих один и тот же набор переменных.

Конечная цель решения системы линейных уравнений – найти значения неизвестных переменных. Вот пример системы линейных уравнений с двумя неизвестными переменными, x и y :

Решение системы линейных уравнений с Numpy

Из предыдущего раздела мы знаем, что для решения системы линейных уравнений необходимо выполнить две операции: инверсию матрицы и матричное точечное произведение. Библиотека Numpy из Python поддерживает обе эти операции. Если вы еще не установили библиотеку Numpy, вы можете сделать это с помощью следующей команды pip :

Теперь давайте посмотрим, как решить систему линейных уравнений с помощью библиотеки Numpy.

Использование методов inv() и dot()

Давайте сначала создадим матрицу A в Python. Для создания матрицы можно использовать метод array модуля Numpy. Матрицу можно рассматривать как список списков, где каждый список представляет собой строку.

Чтобы найти обратную матрицу, матрица передается в метод linalg.inv() модуля Numpy:

Давайте теперь решим систему из трех линейных уравнений, как показано ниже:

Приведенное выше уравнение можно решить с помощью библиотеки Numpy следующим образом:

В приведенном выше скрипте методы linalg.inv() и linalg.dot() соединены вместе. Переменная X содержит решение для уравнения 2 и печатается следующим образом:

Использование метода solve()

Вы можете видеть, что выход такой же, как и раньше.

Реальный Пример

Давайте посмотрим, как система линейных уравнений может быть использована для решения реальных задач.

Предположим, продавец фруктов продал 20 манго и 10 апельсинов за один день на общую сумму 350 долларов. На следующий день он продал 17 манго и 22 апельсина за 500 долларов. Если цены на фрукты оставались неизменными в оба дня, то какова была цена одного манго и одного апельсина?

Эта задача легко решается с помощью системы двух линейных уравнений.

Решение приведенной выше системы уравнений показано здесь:

Результат показывает, что цена одного манго составляет 10 долларов, а цена одного апельсина-15 долларов.

Источник

Инволюта угла

Вычисление инволюты угла и нахождение угла по заданной инволюте.

Поступила вот просьба сделать калькулятор для расчета цилиндрических шестерён — Техника,машиностроение.
Погружаясь в тему шестерён и их расчетов, встретил понятие инволюта, а потом — эвольвента. Показалось занятным и заслуживающим отдельных калькуляторов. Калькуляторы смотри ниже — первый рассчитывает инволюту, два следующих по заданной инволюте находят угол. Интересующимся — текст про инволюту после калькуляторов.

Инволюта угла

Нахождение угла по инволюте методом Ласкина

Нахождение угла по инволюте методом Ченга

Так вот, в дифференциальной геометрии кривых эвольвента — это кривая, нормаль в каждой точке которой является касательной к исходной кривой (см. Эвольвента в Википедии).

Поскольку сразу осознать сказанное выше сложно, перескажу своими словами более образное определение, данное в английской версии статьи (см. Involute on Wikipedia).

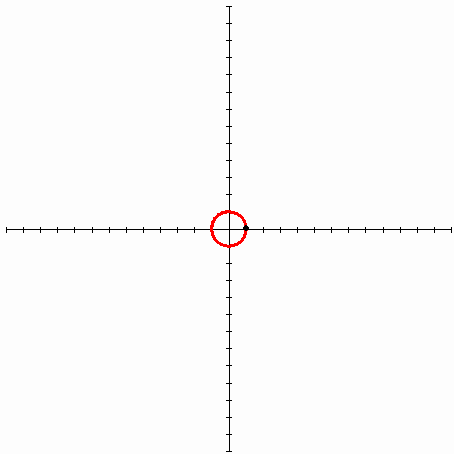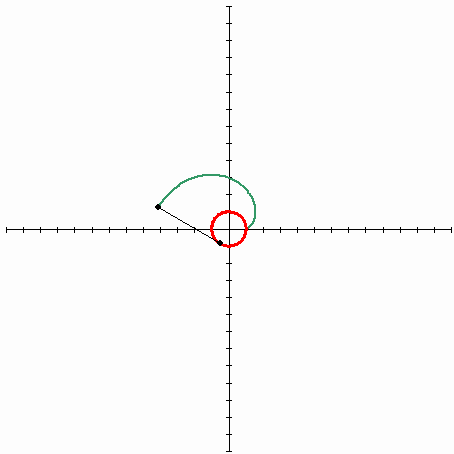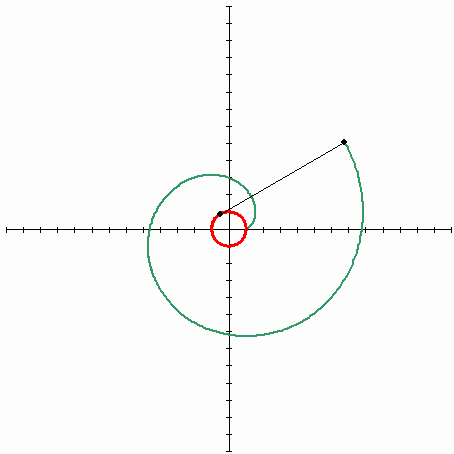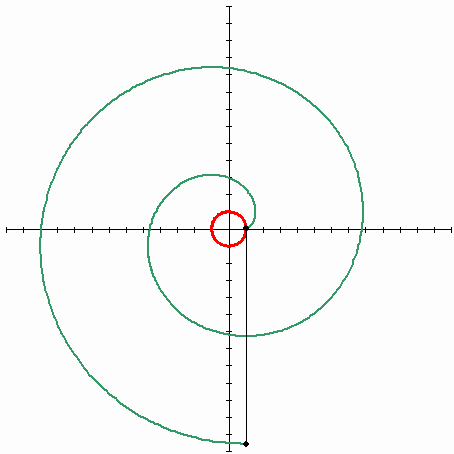
Итак, представим себе катушку ниток, где свободный край нити лежит на катушке. Если взять этот край и начать разматывать нить, все время держа ее натянутой, край нити опишет некую кривую, которая и будет эвольвентой, причем эвольвентой окружности (катушка суть исходная кривая, представляющая собой окружность).

Рисунок ниже изображает эвольвенту окружности (Источник — Википедия). Красная линия — исходная кривая (окружность), черная — натянутая нить, зеленая — траектория конца нити, кривая, называемая эвольвентой окружности.

Думаю, что такое эвольвента, стало более менее ясно после картинки сверху. Теперь разберемся, что это за функция такая.
В этом нам поможет рисунок, который я нарисовал

На рисунке отрезок равен дуге (потому что эта наша «нить»). Угол «фи», соответствующий дуге называется углом развернутости эвольвенты, и состоит суммы угла «тета» (эвольвентного угла) и угла «альфа» (угла давления). Длина дуги

Поскольку — прямоугольный треугольник, то

Вот эта-то функция — и называется инволютой, или эвольвентной функцией.

Уравнения эвольвентной кривой в полярных координатах выглядят так

По построению видно, что угол «альфа» может меняться от 0 до 90, не включая 90, так как в таком случае прямая KK будет параллельна MxN.

Зачем это все? Эвольвента окружности используется в эвольвентном зацеплении — зубчатом зацеплении, в котором профили зубьев очерчены по эвольвенте окружности. При эвольвентном зацеплении общая нормаль к соприкасающимся профилям зубьев всегда совпадает с общей касательной к основным окружностям. Эта касательная называется линией зацепления, так как по ней перемещается точка касания зубьев при движении колёс (картинка). Это наиболее распространенный вид зубчатого зацепления.

А инволюта используется в расчетах, связанных с эвольвентным зацеплением. Причем возникает задача как расчета самой инволюты (что просто), так и обратная задача — нахождение угла давления по его инволюте. Вот обратная задача является не такой простой, ибо уравнение является трансцендентным уравнением, и решить его можно только численными методами.

В завершение рассмотрим численные методы, использованные в калькуляторах выше — метод Ласкина и метод Ченга (подробнее — здесь)

Метод Ласкина (Laskin)
Основан на методе Ньютона, заключающемся в итерационной процедуре вычисления

Ноу-хау, как я понимаю, здесь в выборе начального значения, которое по методу Ласкина вычисляется как
, где I — заданное значение инволюты.

Для вычисления следующих приближений после раскрытия производной получается выражение

В калькуляторе используется пять итераций, но уже четыре должны давать точность до шести знаков после запятой. Метод работает для значений инволюты в диапазоне от 0 до 1, то есть можно находить углы от 0 до 64.87 градусов. На практике этого хватает. Для нахождения инволюты выпускаются таблицы, подобные таблицам тригонометрических функций, так вот там приводимый диапазон углов от 0 до 60.

Метод Ченга (Cheng)
Основан на нахождении приближенного значения с помощью асимптотических кривых. Ченг вывел следующую формулу:

Метод работает для значения инволюты строго меньших 1.8, то есть может находить углы примерно до 71.87 градуса. А дальше оно и не надо — при приближении к 90 тангенс стремится к бесконечности, со всеми вытекающими отсюда последствиями, и, в общем, ну не бывает зубчатых передач с такими большими углами.

Источник

Инвариантность (в математике)

Полезное

Смотреть что такое «Инвариантность (в математике)» в других словарях:

Инвариантность — Инвариант термин, используемый в математике и физике, а также в программировании, обозначает нечто неизменяемое. Кроме того, инварианты используются в олимпиадных задачах по математике для школьников. Абстрактная структурная единица языка фонема … Википедия

Инвариантность — I ж. 1. отвлеч. сущ. по прил. инвариантный I 2. Свойство сохраняться неизменным при определённых преобразованиях переменных (в математике). II ж. 1. отвлеч. сущ. по прил. инвариантный II 2. Отвлеченность от конкретных реализаций (в лингвистике).… … Современный толковый словарь русского языка Ефремовой

ИНВАРИАНТНОСТЬ — [от лат. invarians (invariantis) неизменяющийся] 1) И. в математике св во неизменности по отношению к к. л. преобразованию (условию) или совокупности преобразований. 2) И. в автоматике независимость одной или неск. регулируемых величин в системах … Большой энциклопедический политехнический словарь

Инвариантность — (см. Инвариант) 1) неизменность, независимость от чего либо; 2) (в физике) неизменность какой либо величины при изменении физических условий или (в математике) по отношению к некоторым преобразованиям (к преобразованиям Галилея, Лоренца и т. д.) … Начала современного естествознания

Масштабная инвариантность — или скейлинг свойство уравнений физики, сохранять свой вид при изменении всех расстояний и промежутков времени в одинаковое число раз, то есть Причём здесь подразумевается лишь изменение единиц измерения, само пространство время остаётся… … Википедия

Симметрия (в математике) — Симметрия (от греч. symmetria ‒ соразмерность) в математике, 1) симметрия (в узком смысле), или отражение (зеркальное) относительно плоскости a в пространстве (относительно прямой а на плоскости), ‒ преобразование пространства (плоскости), при… … Большая советская энциклопедия

Симметрия — У этого термина существуют и другие значения, см. Симметрия (значения). «Витрувианский человек» … Википедия

Симметрия — I Симметрия (от греч. symmetria соразмерность) в математике, 1) симметрия (в узком смысле), или отражение (зеркальное) относительно плоскости α в пространстве (относительно прямой а на плоскости), преобразование пространства… … Большая советская энциклопедия

Инварианты — Инвариант термин, используемый в математике и физике, а также в программировании, обозначает нечто неизменяемое. Кроме того, инварианты используются в олимпиадных задачах по математике для школьников. Абстрактная структурная единица языка фонема … Википедия

СИММЕТРИЯ — (от греч. соразмерность), понятие, характеризующее переход объектов в самих себя или друг в друга при осуществлении над ними оп редел. преобразований (преобразований С.); в широком смысле свойство неизменности (инвариантности) некоторых… … Философская энциклопедия

Источник

Три самые известные математические константы: как они появились и зачем нужны

В основе нашей Вселенной стоят числа, также известные как фундаментальные константы. Они показывают, как движутся галактики, как расширяется Вселенная, как вообще работает пространство и время. Рассказываем, кто их открыл и за что отвечает каждое число.

Читайте «Хайтек» в

Что такое математическая константа?

В противоположность переменным величинам существуют математические постоянные. Математическая постоянная, или константа — это величина, значение которой неизменно. Главной отличительной чертой математических констант является их независимость от физических измерений. Все математические константы имеют буквенный символ.

Число Пи

Число Пи (π) — это математическая константа, равная отношению длины окружности к ее диаметру. Десятичное представление числа никогда не заканчивается и является эталоном для высокопроизводительных вычислений.

Чему равно: 3,1415926535…

На сегодняшний день число Пи рассчитали с точностью до 62,8 трлн знаков после запятой — с помощью 32-ядерных процессоров AMD.

Если измерить веревкой длину окружности, получится, что она равна приблизительно трем ее диаметрам. Человечество выяснило это еще в древности. Кстати, это соотношение подходит для любой окружности — неважно, речь о часах или колесе обозрения. Иными словами, все окружности в мире связаны этой математической константой. Еще до нашей эры люди знали, что это число чуть больше трех. Вопрос в том, насколько. Столетия эта загадка не давала покоя мыслителям, поскольку имела большое значение и была почти высчитана. Но это «почти» растянулось на несколько тысяч лет.

Точное авторство числа Пи неизвестно. Вообще, открытие приписывается древним индийцам, грекам, китайцам и прочим хорошим людям. Впервые обозначил его греческой буквой π в начале XVIII века английский математик Уильям Джонс.

Числу π столько же лет, сколько всей математике: около 4 тыс. Старейшие шумерские таблички приводят для него цифру 25/8, или 3,125. Ошибка — меньше процента. Вавилоняне абстрактной математикой особо не увлекались, так что π вывели опытным путем, просто измеряя длину окружностей. Кстати, это первый эксперимент по численному моделированию мира.

Число Бога

Число Фи (φ) — число Бога, Золотое Сечение, Золотая Пропорция — у него много названий. Сам по себе это отношение одной части чего-либо к другой с коэффициентом 1,618 (это 61,8%), или 62% на 38%.

Чему равно: 1,6180339887…

Классическое определение Золотой Пропорции: меньшее относится к большему так, как большее относится к целому, с коэффициентом 1,618.

Принято считать, что впервые закономерности соотношения размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 году немецкий исследователь Цейзинг в своем научном труде «Эстетические исследования». За основу своей теории он взял учение о Золотом Сечении.

Еще в VI веке до н. э. древнегреческий философ и математик Пифагор ввел в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.

История Золотого Сечения связана еще с одним известным итальянским математиком Фибоначчи. До наших времен дошел ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д., известный как ряд Фибоначчи.

Особенность последовательности данных чисел заключается в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению Золотого Сечения (21:34=0,617, а 34:55=0,618). Впоследствии все исследователи Золотого Сечения в растительном и животном мире, искусстве и анатомии приходили к этому ряду как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибоначчи вывел, подсчитывая количество рожденных кроликов от пары кроликов за год.

Число Непера

Число е — своего рода двойник π. Если π отвечает за пространство, то е — за время, и тоже проявляет себя почти всюду. Скажем, радиоактивность полония-210 уменьшается в е раз за средний срок жизни одного атома, а раковина моллюска Nautilus — это график степеней е, обернутый вокруг оси.

Чему равно: 2,718281828…

е — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Приблизительно равно 2,71828. Иногда его называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».

Иными словами, число е является базовым соотношением роста для всех непрерывно растущих процессов. Оно участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов и других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е — это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.

Число открыл Джон Непер, шотландский математик, в 1618 году. Самого числа он не упоминал, зато выстроил на его основе свои таблицы логарифмов. Одновременно кандидатами в авторы константы считаются Якоб Бернулли, Лейбниц, Гюйгенс и Эйлер. Достоверно известно только то, что символ е взялся из фамилии последнего.

Как и π, е — трансцендентное число. Говоря проще, его нельзя выразить через дроби и корни. Есть гипотеза, что у таких чисел в бесконечном «хвосте» после запятой встречаются все комбинации цифр, какие только возможны.

Источник

E (математическая константа)

Играет важную роль в дифференциальном и интегральном исчислении, а также многих других разделах математики.

2,718 281 828 459 045 235 360 287 471 352 662 497 757… [1]

Содержание

Способы определения

Число e может быть определено несколькими способами.

Свойства

История

Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен .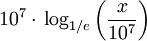

Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует (см.: Непер).

Предполагается, что автором таблицы был английский математик Отред.

Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:

Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.

Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.

Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler ).

Способы запоминания

Доказательство иррациональности

Пускай рационально. Тогда , где и целые положительные, откуда

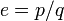
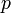
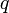
Умножая обе части уравнения на 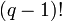, получаем

Переносим 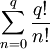в левую часть:

Все слагаемые правой части целые, следовательно:

— целое

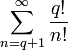
Но с другой стороны

Интересные факты

Источник