Что такое унимодальная функция

Что такое унимодальная функция

Давайте дадим определение унимодальных и бимодальных функций. Значение их очень велико, т.к. нередко сложные задачи разбиваются на простые, а в них требуется искать экстремумы унимодальных функций.

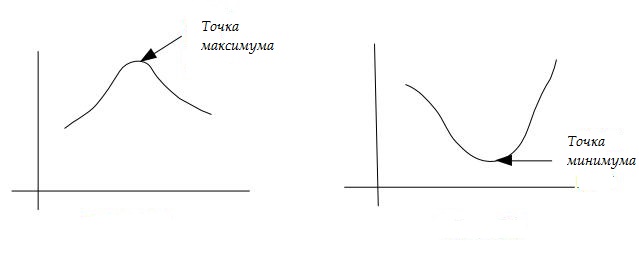
Функция f(x) называется унимодальной функцией, если для некоторого значения m она монотонно увеличивается при x≤m и монотонно уменьшается при x≥m. для функции f(x) максимальное значение равно f (m), и другого локального максимума нет.

На рисунке слева график имеет только одну максимальную точку, а остальная часть графика идет вниз оттуда, а на рисунке справа график имеет только одну минимальную точку, а остальная часть графика идет вверх оттуда. Таким образом, можно сказать, что если функция имеет глобальный максимум или глобальный минимум, то она рассматривается как унимодальная функция.

Рассмотрим функцию f (x) в интервале [a, b], и мы должны определить значение x, для которого функция максимизируется. Функция строго увеличивается в интервале [a, x] и строго уменьшается в интервале [x, b]. Для этого мы можем использовать модифицированный двоичный поиск, чтобы определить максимум или значение этой функции.

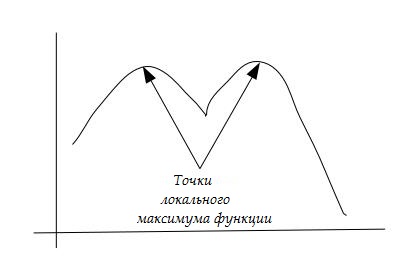
Функция называется бимодальной функцией, если она имеет два локальных минимума или максимума. Обычно бимодальная функция указывает на две различные группы. Например, в классе есть много студентов, получающих оценку A и много получающих оценку D. Это говорит нам, что в классе есть две разные группы студентов, одна группа недостаточно подготовлена, а другая группа чрезмерно подготовлена. Смотрите этот рисунок для лучшего понимания:

С бимодальной функцией и выше мы не знаем, является ли экстремум локальным или глобальным, если мы не знаем весь график. С унимодальной функцией любой экстремум, который мы находим, гарантированно является глобальным экстремумом.

заметки, математика

Источник

Понятие унимодальности функций

Функция называется унимодальной, если она имеет единственный локальный минимум (максимум) на всей допустимой области. Для унимодальной функции локальный минимум (максимум) является также и глобальным.

Функция на этом рисунке не является унимодальной, ни в случае поиска минимума, ни в случае поиска максимума функции f(x).
Интервал унимодальности – область, внутри допустимой, в которой функция является унимодальной. Понятие унимодальности связано с направлением оптимизации.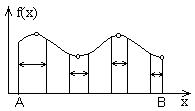

3.7. Градиент и линии уровня

Для геометрической интерпретации данной (двумерной) задачи необходимо на плоскости показать область допустимых значений переменных и и привести несколько характерных линий уровня.

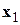
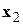
Градиент функции – вектор, показывающий направление наибольшего возрастания функции в заданной точке.

Антиградиент – вектор, показывающий направления наибольшего убывания функции в заданной точке.

– вектор частных производных.

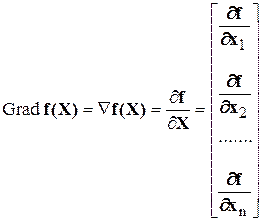
Вектор антиградиента равняется –Grad. Вектор Grad перпендикулярен касательной к линии уровня, проходящий через данную точку.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Двумерные тестовые функции для оптимизации

Оптимизация функций — это область исследований, где поставлена задача найти некое входное значение [аргумент функции], результат которого — максимум или минимум данной функции. Алгоритмов оптимизации много, поэтому важно развивать алгоритмическое чутьё и исследовать алгоритмы на простых и легко визуализируемых тестовых функциях.

Двумерные функции принимают два входных значения (x и y) и выводят единожды вычисленное на основе входа значение. Эти функции — одни из самых простых для изучения оптимизации. Их преимущество в том, что они могут визуализироваться в виде контурного графика или графика поверхности, показывающего топографию проблемной области с оптимумом и уникальными элементами, которые отмечены точками. В этом туториале вы ознакомитесь со стандартными двумерными тестовыми функциями, которые можно использовать при изучении оптимизации функций. Давайте начнём.

Обзор туториала

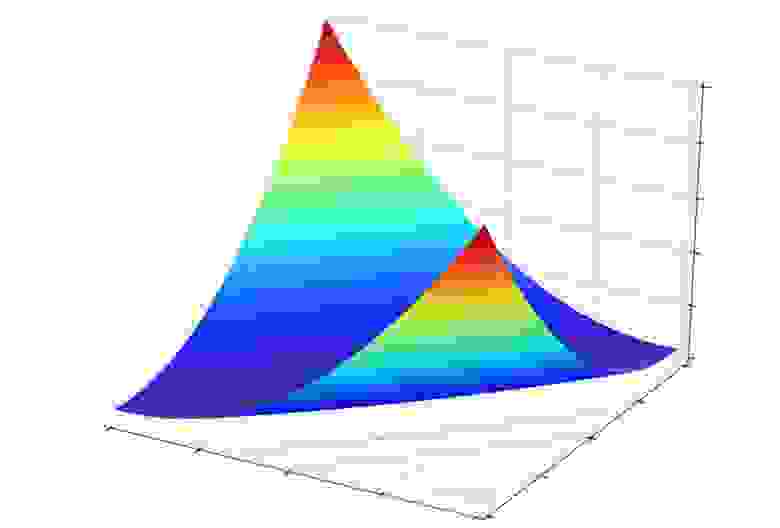
Двумерная функция — это функция, которая принимает две входные переменные и вычисляет целевое значение. Можно представить две входные переменные как две оси на графике, x и y. Каждый вход в функцию является единственной точкой на графике, а результат вычисления функции — некоторая высота на графике.

Такая визуализация позволяет концептуализировать функцию в виде поверхности, так мы сможем охарактеризовать функцию по структуре поверхности. Например, возвышенности указывают на большие значения целевой функции, а провалы — на небольшие.

Поверхность может иметь один основной оптимум или же много точек для оптимизации, в которых можно, говоря образно, застрять. Также она может быть гладкой, шумной, выпуклой, может иметь иные всевозможные свойства, которые важны в смысле алгоритмов оптимизации. Мы могли бы использовать множество других типов двумерных функций.

Вместе с тем, есть много стандартных тестовых функций, применяемых в области оптимизации, а также тестовые функции со специфическими свойствами, которые мы можем применять, когда тестируем различные алгоритмы. Рассмотрим несколько простых двумерных тестовых функций, разделив их на две группы согласно свойствам:

Унимодальные функции.

Унимодальная функция 1.

Унимодальная функция 2.

Унимодальная функция 3.

Мультимодальные функции.

Мультимодальная функция 1.

Мультимодальная функция 2.

Мультимодальная функция 3.

Реализация каждой целевой функции будет представлена на Python в выведена в виде поверхности.

Все целевые функции являются функциями минимизации, то есть задача — найти аргументы, при которых значение функции минимально. Любая максимизирующая функция может быть заменена функцией минимизации путем добавления минуса ко всем её значениям. Аналогичным образом минимизирующая функция заменяется максимизирующей. Кроме того, все функции взяты из литературы, их придумал не я. Ссылки смотрите в разделе «Дальнейшее чтение».

Вы можете выбрать, скопировать и вставить в код одну или несколько функций, чтобы использовать их в вашем собственном проекте, посвящённом изучению или сравнению поведения алгоритмов оптимизации.

Унимодальные функции

Унимодальность означает, что функция имеет единственный глобальный оптимум.

Унимодальная функция может быть выпуклой и невыпуклой. Выпуклая функция — это функция, на графике которой между двумя любыми точками можно провести линию и эта линия останется в домене. В случае двумерной функции это означает, что поверхность имеет форму чаши, а линии между двумя точками проходят по чаше или внутри неё. Давайте рассмотрим несколько примеров унимодальных функций.

Унимодальная функция 1

Код создаёт поверхность согласно графику функции.

График поверхности на основе унимодальной функции оптимизации 1

Унимодальная функция 2

Код создаёт поверхность согласно графику функции.

График унимодальной функции оптимизации 2

Унимодальная функция 3

Код создаёт поверхность согласно графику функции.

График унимодальной функции оптимизации 3

Мультимодальные функции

Мультимодальная функция — это функция с более чем одной “модой” или оптимумом (например долиной на графике).

Мультимодальные функции являются невыпуклыми. Могут иметь место один или несколько ложных оптимумов. С другой стороны, может существовать и несколько глобальных оптимумов, например несколько различных значений аргументов функции, при которых она достигает минимума.

Вот несколько примеров мультимодальных функций.

Мультимодальная функция 1

Код создаёт поверхность согласно графику функции.

Мультимодальная функция оптимизации 1

Мультимодальная функция 2

Код создаёт поверхность согласно графику функции.

Мультимодальная функция оптимизации 2

Мультимодальная функция 3

Код создаёт поверхность согласно графику функции.

График мультимодальной функции оптимизации 3

Резюме

Если вы хотите глубже погрузиться в тему — обратите внимание на сопутствующие материалы ниже.

Узнайте, как прокачаться в других специальностях или освоить их с нуля:

Источник

Унимодальность

СОДЕРЖАНИЕ

Унимодальное распределение вероятностей [ править ]

Рисунки 2 и 3 иллюстрируют бимодальные распределения.

Другие определения [ править ]

Существуют и другие определения унимодальности в функциях распределения.

Использование и результаты [ править ]

Неравенства [ править ]

Неравенство Гаусса [ править ]

Неравенство Высочанского – Петунина [ править ]

Режим, медиана и среднее значение [ править ]

Гаусс также показал в 1823 г., что для унимодального распределения [10]

Для унимодального распределения можно показать, что медиана ν и среднее значение μ лежат в пределах (3/5) 1/2 ≈ 0,7746 стандартных отклонений друг от друга. [11] В символах,

В 2020 году Бернард, Каззи и Вандуффель обобщили предыдущее неравенство, получив максимальное расстояние между симметричным средним квантилем и средним значением, [12] q α + q ( 1 − α ) 2 <\displaystyle <\frac +q_<(1-\alpha )>><2>>>

Аналогичное соотношение имеет место между медианой и модой θ : они лежат в пределах 3 1/2 ≈ 1,732 стандартных отклонений друг от друга:

Также можно показать, что среднее значение и мода лежат в пределах 3 1/2 друг от друга.

Асимметрия и эксцесс [ править ]

Рохатги и Секели показали, что асимметрия и эксцесс унимодального распределения связаны неравенством: [13]

Клаассен, Моквельд и ван Эс вывели неравенство, немного отличающееся от неравенства, полученного Рохатги и Секели (показано выше), которое имеет тенденцию быть более всеобъемлющим (т. Е. Давать больше положительных результатов) в тестах на унимодальность: [14]

Унимодальная функция [ править ]

Доказать унимодальность зачастую сложно. Один из способов состоит в использовании определения этого свойства, но оказывается, что он подходит только для простых функций. Существует общий метод, основанный на производных [15], но он не дает успеха для каждой функции, несмотря на свою простоту.

Примеры унимодальных функций включают квадратичные полиномиальные функции с отрицательным квадратичным коэффициентом, функции отображения палатки и многое другое.

Другие расширения [ править ]

В вычислительной геометрии, если функция является унимодальной, это позволяет разработать эффективные алгоритмы для поиска экстремумов функции. [18]

Более общее определение, применимое к функции f (X) векторной переменной X, состоит в том, что f является унимодальным, если существует взаимно однозначное дифференцируемое отображение X = G ( Z ) такое, что f ( G ( Z )) является выпуклый. Обычно требуется, чтобы G ( Z ) была непрерывно дифференцируемой с невырожденной матрицей Якоби.

Источник

Определение и свойства унимодальных и многомодальных функций

Метод многомерного поиска первого порядка – наискорейшего спуска

На каждой итерации задача одномерной оптимизации решается точно.

При использовании метода наискорейшего спуска на каждой итерации величина шага λ k выбирается из условия минимума функции f(x) в направлении спуска.

Прямой метод Хука-Дживса для решения задач многомерного поиска

Метод нелинейной оптимизации нулевого порядка – не использующий значения производных функций, применяется в том случае, если значения производных сложно получить в виде аналитических функций или процесс вычисления производных довольно трудоемкий.

Метод Хука-Дживса для поиска безусловного локального экстремума функции. Алгоритм делится на две фазы: исследующий поиск и поиск по направлению.

Прямой метод Гаусса для решения задач многомерного поиска

Одномерный поиск на унимодальных функциях: метод Фибоначчи

Одномерный поиск на унимодальных функциях: метод золотого сечения

Одномерный поиск на унимодальных функциях: метод дихотомии

Классификация численных методов решения задач нелинейного программирования

Численные методы – в которых решение задачи НП ищется эвристическим подбором значений неизвестных, доставляющих экстремум min или max целевой функции.

( набор расчетных точек фиксировано (значение очередной расчетной точки

и определено априорно) определяется по рез-ту предыд. итерации)

Пассивный (выбор стартовой точки) => переход к последовательному.

d 2 f / d x 2 2 f / d x 2 > 0 – второго порядка

Численные методы многомерных задач сводится к комбинации одномерных.

Метод неопределенных множителей Лагранжа для решения задач нелинейного программирования

Определение и свойства унимодальных и многомодальных функций

Унимодальная функция – на интервале от а до b, если внутри этого интервала существует точка, слева от которой функция только возрастает, справа – убывает.

Основное свойство унимодальных функций, используемое при поиске точек минимума, состоит в том, что вычисление любых двух значений f(x₁), f(x₂), x₁ ¹ x₂, x₁,x₂ Î [a,b] позволяет уменьшить интервал поиска точки минимума. Для решения задачи одномерной оптимизации с унимодальной целевой функцией применяется метод золотого сечения и метод чисел Фибоначчи.

Многомодальная функция – содержит внутри интервала [a, b] несколько точек аналогичных свойству унимодальной.

Задачи нелинейного программирования решаются так: дифференциал означает, что функция определена в сколь угодно малой окрестности возле точки вычисления производно.

grad [f(x)] = 0 – вектор, указывающий направление возрастающей функции.

1) На области допустимых значений находятся все точки (grad = 0 или производная = 0).

2) С помощью специальных методов находятся все значения целевой функции на границах допустимых значений.

3) Простым переборным сравнением среди стац. и граничных точек, выбирается точка, соотв. наибольшим или наименьшим значением целевой функции.

Источник