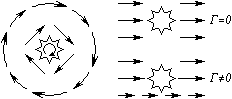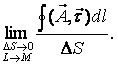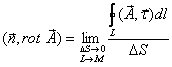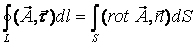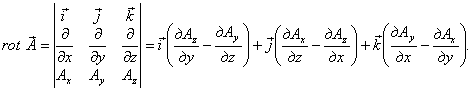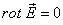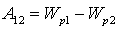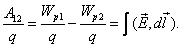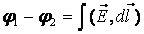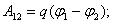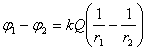Что такое циркуляция векторного поля
Циркуляция векторного поля. Ротор вектора. Теорема Стокса
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Пусть в некоторой области G задано непрерывное векторное поле а ) к и замкнутый ориентированный контур L. Определение 1. Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от оектора а по контуру L Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, оп- Рис. 31 ределяемымориентацией контура (рис. 31); символ f означает, что интеграл берется по зам1«угому контуру L. ь
Ротор (вихрь) векторного поля Рассмотрим поле вектора Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам. Огределенив 2. Ротором вектора »(М) называется вектор, обозначаемый символом rot а и определяемый равенством или, в символической, удобной для запоминания форме, Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,
Определение 3. Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называете я безвихревым. Пример 2. Найти ротор вектора 4 Согласно формуле (3) имеем Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим Таким образом, поле вектора rot а соленоида л ьно.
Теорема 7 (Стокса). Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L, При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Е, и что ориентация орта нормали п° к поверхности ЕС G согласована с ориентацией контура L так, что из конца нормши обход контура в заданном направлении виден совершающимся против часовой стрелки.
Возможно вам будут полезны данные страницы:
Пусть — уравнение поверхности Е и функция ф(х>у) непрерывна и имеет непрерывные частные производные gf и ^ в замкнутой области D.
Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора Складывая равенства почленно, получим формулу Стокса (5), или, короче, Замечание 1. Мы показали, что поле вектора rote — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Е, натянутой на контур L. Замечание 2. Формула (4) выведена в предположении, что поверхность £ однозначно проектируется на все три координатные плоскости. Бели это условие не выполнено, то разбиваем £ на частя так, чтобы каждая часть указанному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.
Пример 3:
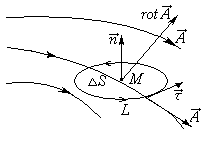
Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению, Здесь (Е) — плоская площадка, перпендикулярная вектору л; 5 — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; (Е) М означает, что площадка (Е) стягивается к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33). 4
Применим сначала к циркуляции (a,dr) вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении: откуда (скалярное произведение берется в некоторой средней точке Мф площадки (Е)). Пристягивании площадки (Е) кточке М средняяточка Л/ср тоже стремится кточ-ке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем Поскольку проекция вектора rot а на произвольное направление не зависитотвы-бора системы координат,то и сам вектор rota инвариантен относительно этого выбора.
Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rota согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта. 8.3.
| Физический смысл ротора поля Пустьтвердое |
тело вращается вокруг неподвижной оси I с угловой скоростью и. Не нарушая общности, можно считать, что ось I совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где Вектор угловой скорости в нашем случае равен из = wk, вычислим вектор v линейной скорости точки М, Отсюда Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля.
Правила вычисления ротора
Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения. 8.4. Правила вычисления ротора 1. Ротор постоянного вектора с равен нулевому вектору, 2. Ротор обладает свойством линейности постоянные числа. 3. Ротор произведения скалярной функции и<М) на векторную а(М) вычисляется по формуле
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Циркуляция векторного поля и её вычисление
Определение 5.3. Циркуляцией Ц векторного поля а = а(М) называется линейный интеграл, взятый вдоль замкнутой ориентированной кривой L. Таким образом, по определению
где символ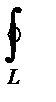 
означает интеграл по замкнутой кривой L.
Если векторное поле а = а(М) задано в координатой форме
то циркуляция векторного поля будет равна
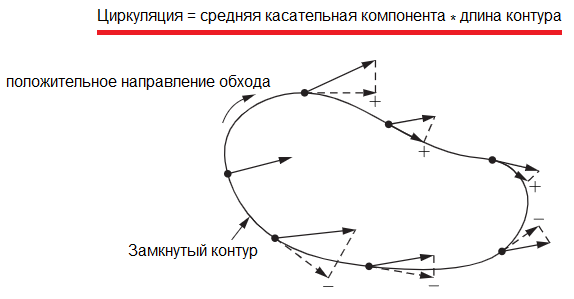
За положительное направление обхода замкнутой кривой L будем считать направление, при котором область, ограниченная этой кривой, будет оставаться слева.
Пример 5.5. Вычислить циркуляцию векторного поля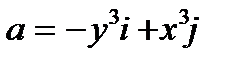 
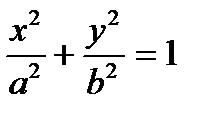
вдоль эллипса L: 
.
Решение. По определению циркуляции имеем
(5.4)
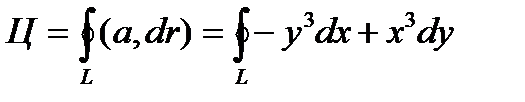
Параметрические уравнения данного эллипса имеют вид (рис. 5.3)
(5.5)
(5.6)
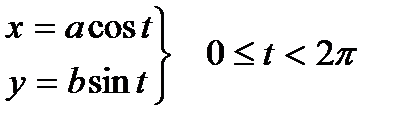
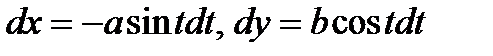
Подставляя (5.5) и (5.6) в (5.4), получим
аналогично находим, что
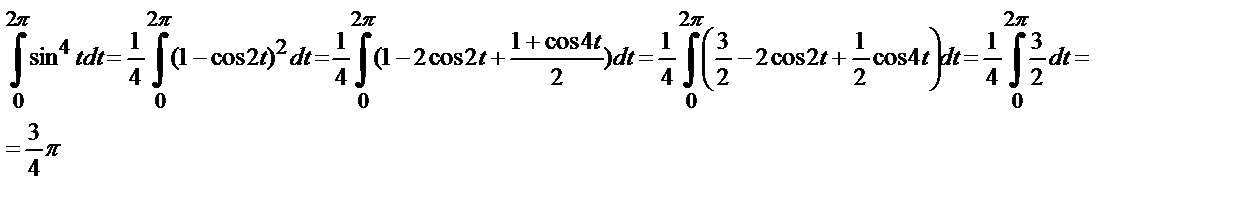
Пример 5.6. Вычислить циркуляцию векторного поля
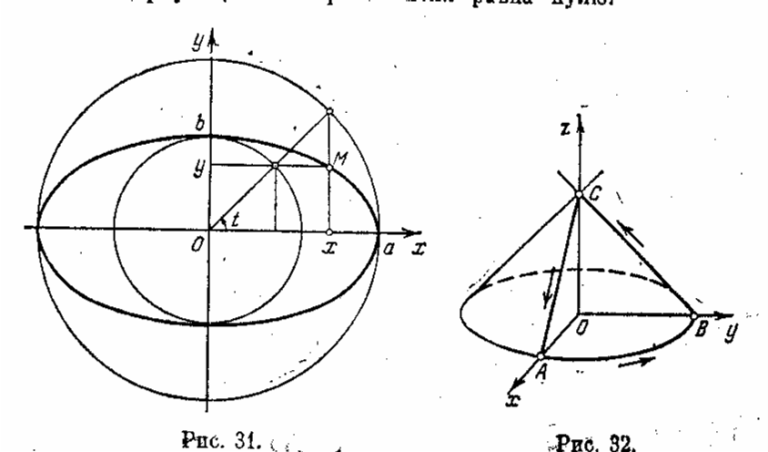
вдоль линии L, получаемой пересечением конуса x 2 + y 2 = (z-1) 2 с координатными плоскостями (р 11.4)
Решение. Линия L состоит из двух отрезков ВС и СА, расположенных на координатных плоскостях YOZ и XOZ соответственно и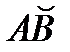 
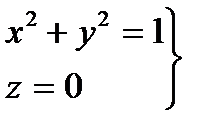
окружности 
. Поэтому циркуляция данного векторного поля будет равна
1. На отрезке ВС имеем
2. на отрезке СА имеем
3. На дуге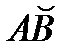 
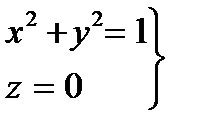
окружности 
имеем z = 0, dz = 0, и значит
Искомая циркуляция векторного поля равна нулю.
Пример 5.7. Вычислить циркуляцию векторного поля a = xyi + yzj + xzk, если
Решение. Имеем 
Линия L есть эллипс, получающийся в результате сечения цилиндра x 2 + y 2 = 1 плоскостью x + y + z = 1. Найдем параметрические уравнения этой линии. Проекция любой точки линии на плоскость ХОУ находится на окружности x 2 + y 2 = 1. Отсюда получаем x = cost, y = sint. Но
Рис. 5.3 Рис. 5.4
Поток и циркуляция векторного поля
П о материалам лекции Ричарда Фейнмана
При описании законов электричества с точки зрения векторных полей, перед нами открываются две математически важные характеристики векторного поля: поток и циркуляция. Хорошо бы разобраться, что это за математические понятия и в чем заключается их практический смысл.
На вторую часть вопроса легко ответить сразу, ведь понятия потока и циркуляции лежат в основе уравнений Максвелла, на которых, по сути, и держится вся современная электродинамика.
Так, например, закон электромагнитной индукции может быть сформулирован следующим образом: циркуляция напряженности электрического поля E по замкнутому контуру C равна скорости изменения потока магнитного поля B через площадь поверхности S, ограниченной данным контуром С.
Далее мы достаточно просто, на понятных примерах с жидкостью, опишем то, как математически определяются, из чего берутся и получаются данные характеристики поля.
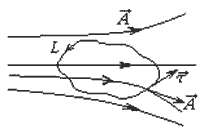
Поток векторного поля
Для начала давайте изобразим вокруг исследуемой области пространства некую замкнутую поверхность совершенно произвольной формы. После того как мы эту поверхность изобразим, зададимся вопросом, вытекает ли через данную замкнутую поверхность исследуемый объект, который мы именуем полем? Чтобы понять о чем здесь идет речь, рассмотрим простой пример с жидкостью.
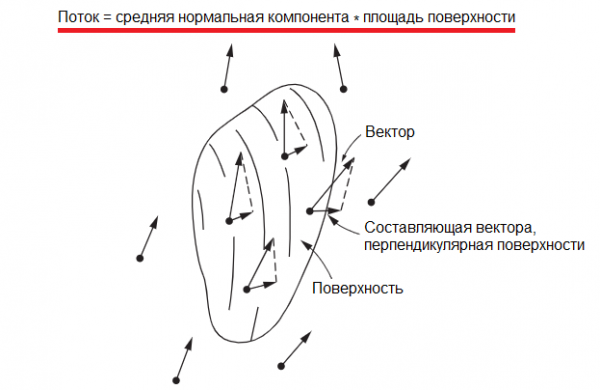
Словосочетанием «поток векторного поля» (а для нашего примера более точным будет выражение «поток скорости жидкости») договоримся именовать общее количество воображаемой жидкости, которая именно вытекает наружу через поверхность из рассматриваемого объема, ограниченного данной замкнутой поверхностью (для потока скорости жидкости — сколько жидкости вытекает из объема за единицу времени).
В результате, поток через элемент поверхности окажется равен произведению площади элемента поверхности на перпендикулярную составляющую скорости. Тогда общий (суммарный) поток через всю поверхность будет равен произведению средней нормальной составляющей скорости, которую будем отсчитывать изнутри наружу, на общую площадь поверхности.
Теперь вернемся к электрическому полю. Электрическое поле, конечно, нельзя считать скоростью течения какой-то жидкости, однако мы имеем право ввести математическое понятие потока, похожее на то, что мы описали выше как поток скорости жидкости.
Только в случае с электрическим полем, его поток может быть определен через среднюю нормальную компоненту напряженности электрического поля Е. Кроме того, поток электрического поля можно определить не обязательно через замкнутую поверхность, а через любую ограниченную поверхность, обладающую не равной нулю площадью S.
Циркуляция векторного поля
Всем хорошо известно, что поля можно для наглядности изображать в виде так называемых силовых линий, в каждой точке которых направление касательной совпадает с направлением напряженности поля.
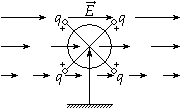
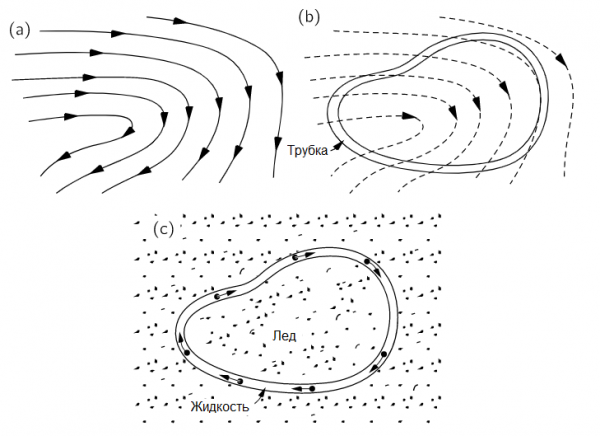
Опять вернемся к аналогии с жидкостью и представим себе поле скоростей жидкости. Зададимся вопросом: циркулирует ли жидкость? То есть движется ли она преимущественно по направлению какого-то воображаемого замкнутого контура?
Для наглядности представим, что жидкость в неком большом сосуде как-то движется (рис a), и мы резко заморозили почти весь ее объем, но умудрились оставить не замороженным объем в форме ровной замкнутой трубки, в которой трение жидкости о стенки отсутствует (рис b).
За пределами этой трубки жидкость превратилась в лед, и поэтому больше не может двигаться, однако внутри трубки жидкость способна продолжить свое движение при условии что имеется преобладающий импульс, который гонит ее, например по часовой стрелке (рис c). Тогда произведение скорости жидкости в трубке на длину трубки мы и назовем циркуляцией скорости жидкости.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Лекция 5
1.Работа электрического поля
Из механики известно определение элементарной работы силы
Пусть в электрическом поле существует точечный заряд, который под действием поля перемещается из точки 1 в точку 2.
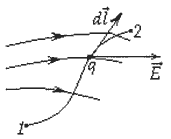
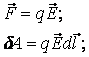
Считается, что заряд постоянный. Таким образом, работа равна криволинейному интегралу от напряженности, вычисленному вдоль траектории.
2.Работа в поле точечного заряда
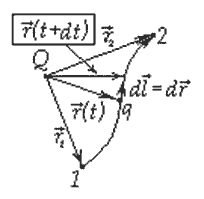
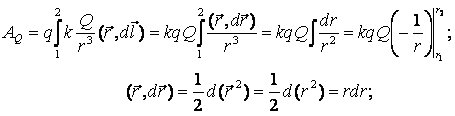
Очевидно, что данная работа не зависит от формы траектории, а зависит только от начального и конечного положения заряда. Можно сделать вывод о том, что если заряд перемещается по замкнутой траектории, то работа поля равна нулю. Таким образом, можно записать
3.Теорема о циркуляции
Пусть поле создано системой точечных зарядов. Вычислим интеграл от напряженности по замкнутой траектории.
Данное утверждение и составляет суть теоремы о циркуляции. В математике подобный интеграл называют циркуляцией.
.
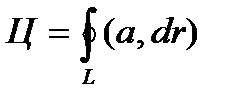
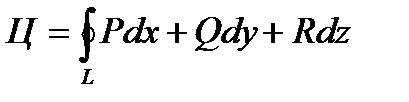
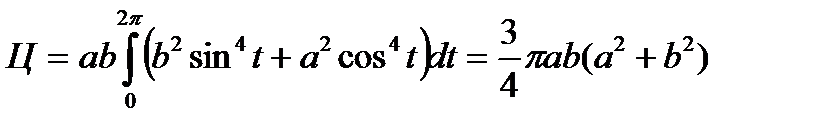
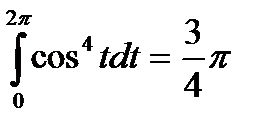
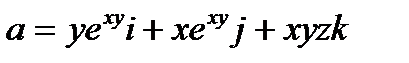
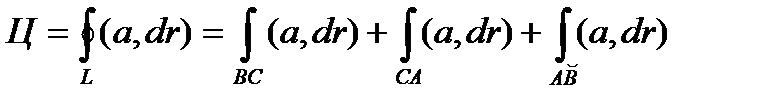
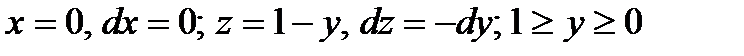
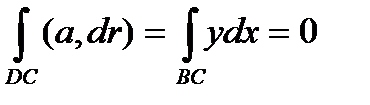
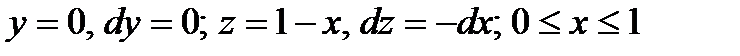
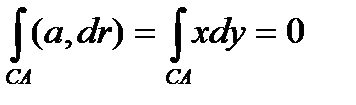
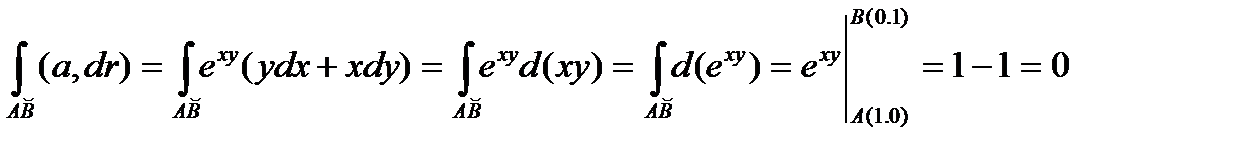
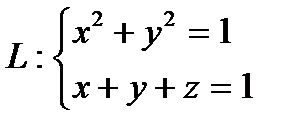
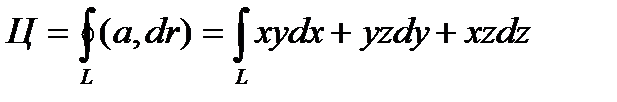
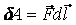
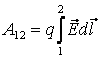
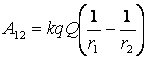
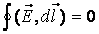
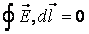
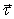— единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.
