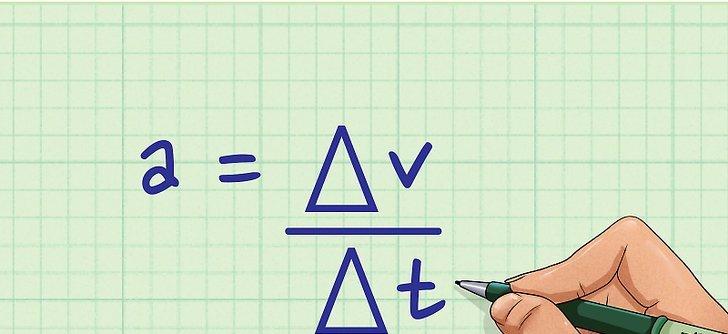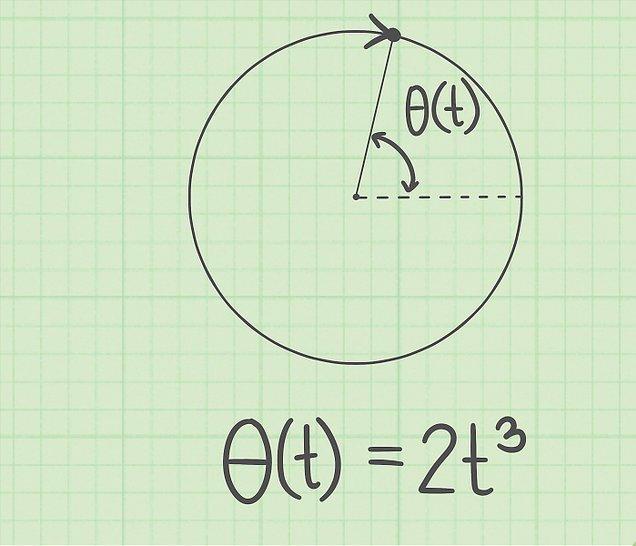что такое скорость ускорение
Формулы вычисления ускорения через скорость. Пример задачи
Каждый школьник сможет дать ответ на вопрос, что такое скорость. Под ней понимают физическую величину, которая определяет быстроту прохождения телом расстояний, что математически выражается через производную пути l по времени t:
В системе СИ скорость принято измерять в метрах в секунду (м/с).
Если взять теперь производную по времени t от скорости v, то мы получим ускорение a:
Заметим, что ускорение может быть также рассчитано, как вторая производная по времени от пути. Величина a показывает быстроту, с которой изменяется величина v. Как правило, ускорение определяют в метрах в секунду в квадрате (м/с2).
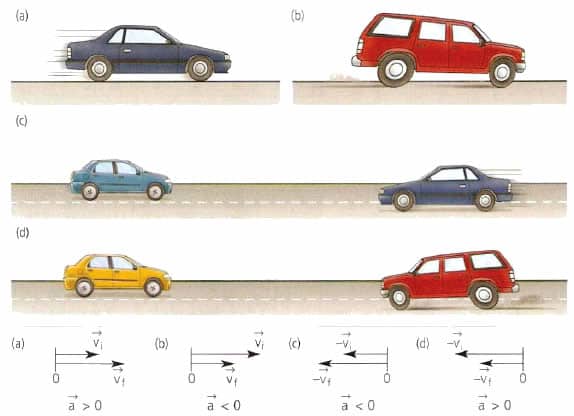
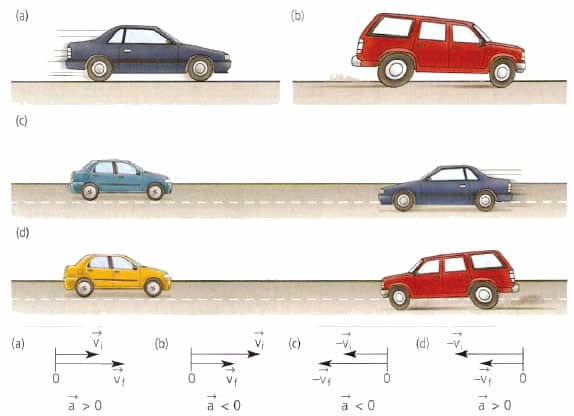
Величины a и v являются векторными. Скорость направлена по касательной к траектории, а ускорение совпадает с вектором изменения скорости.
Равноускоренное (равнозамедленное) движение по прямой
Когда тело движется вдоль прямой линии с постоянным ускорением, то есть a=const, то существует всего три формулы определения ускорения через скорость и время:
Первое выражение позволяет определить ускорение, если тело начало ускоренное движение из состояния покоя. Оно отличается от математического определения ускорения тем, что в данном случае определяется средняя величина a за время движения t. Второе выражение также справедливо для ускоренного движения, только в этом случае до возникновения ускорения тело уже имело скорость v0. Наконец, третья формула применяется тогда, когда тело замедляет свое движение (тормозит) с постоянным ускорением.
Отметим, что все три равенства предполагают линейную зависимость между величинами a и v.
Пример решения задачи
Автомобиль двигался по трассе со скоростью 80 км/ч. Затем он начал тормозить и остановился ровно через 1 минуту. Необходимо определить его среднее ускорение торможения.
Прежде чем пользоваться записанной в предыдущем пункте формулой ускорения через скорость, переведем известные из условия задачи величины в единицы СИ:
v0 = 80 км/ч = 22,22 м/с;
Поскольку автомобиль в итоге остановился, то v = 0. Подставим все известные значения в соответствующую формулу, получим:
a = (v0-v)/t = 22,22/60 = 0,37 м/с2.
Рассчитанная величина не является слишком большой по сравнению с ускорением, которое наша планета сообщает всем телам (9,81 м/с2).
Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений
Как известно, любая физическая величина относится к одному из двух типов, она является либо скалярной, либо векторной. В данной статье рассмотрим такие кинематические характеристики как скорость и ускорение, а также покажем, куда направлены векторы ускорения и скорости.
Что такое скорость и ускорение?
Обе величины, названные в этом пункте, являются важными характеристиками любого вида движения, будь то перемещение тела по прямой линии или по криволинейной траектории.

Скоростью называется быстрота изменения координат во времени. Математически эта величина равна производной по времени пройденного пути, то есть:
Здесь вектор l¯ направлен от начальной точки пути к конечной.
В свою очередь ускорение – это скорость, с которой изменяется во времени сама скорость. В виде формулы оно может быть записано так:
Очевидно, что взяв вторую производную от вектора перемещения l¯ по времени, мы также получим значение ускорения.
Поскольку скорость измеряется в метрах в секунду, то ускорение, согласно записанному выражению, измеряется в метрах в секунду в квадрате.
Куда направлены векторы ускорения и скорости?
Вектор скорости тела направлен в сторону движения всегда, независимо от того, замедляется или ускоряется тело, движется оно по прямой или по кривой. Если говорить геометрическими терминами, то вектор скорости направлен по касательной к точке траектории, в которой в данный момент находится тело.
Вектор ускорения точки материальной или тела не имеет ничего общего со скоростью. Этот вектор направлен в сторону изменения скорости. Например, для прямолинейного движения величина a¯ может как совпадать по направлению с v¯, так и быть противоположной v¯.
Действующая на тело сила и ускорение
Мы выяснили, что вектор ускорения тела направлен в сторону изменения вектора скорости. Тем не менее не всегда можно легко определить, как меняется скорость в данной точке траектории. Более того, для определения изменения скорости необходимо выполнить операцию разности векторов. Чтобы избежать этих трудностей в определении направления вектора a¯, существует еще один способ быстро его узнать.
Ниже записан знаменитый и хорошо известный каждому школьнику закон Ньютона:
Формула показывает, что причиной возникновения ускорения у тел является действующая на них сила. Поскольку масса m является скаляром, то вектор силы F¯ и вектор ускорения a¯ направлены одинаково. Этот факт следует запомнить и применять на практике всегда, когда возникает необходимость в определении направления величины a¯.
Если на тело действуют несколько разных сил, тогда направление вектора ускорения будет равно результирующему вектору всех сил.
Движение по окружности и ускорение
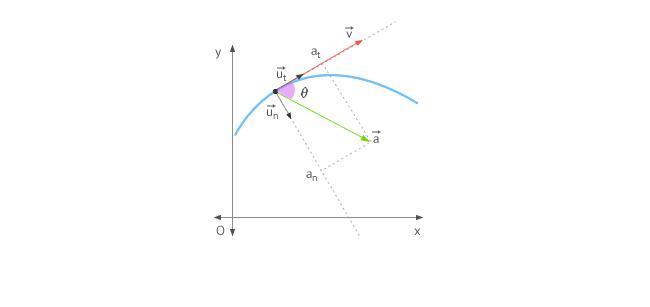
Когда тело перемещается по прямой линии, то ускорение направлено либо вперед, либо назад. В случае же движения по окружности ситуация усложняется тем, что вектор скорости постоянно меняет свое направление. В виду сказанного, полное ускорение определяется двумя его составляющими: тангенциальным и нормальным ускорениями.
Тангенциальное ускорение направлено точно так же, как вектор скорости, или против него. Иными словами, эта компонента ускорения направлена вдоль касательной к траектории. Ускорение тангенциальное описывает изменение модуля самой скорости.
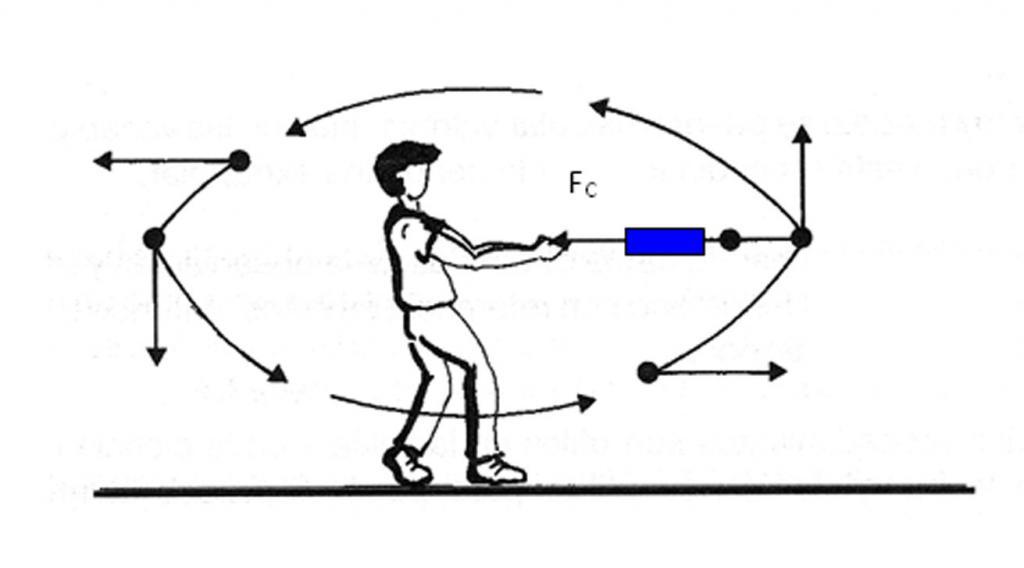
Ускорение нормальное направлено вдоль нормали к данной точке траектории с учетом ее кривизны. В случае движения по окружности вектор этой компоненты указывает на центр, то есть нормальное ускорение направлено вдоль радиуса вращения. Эту компоненту часто называют центростремительной.
Полное ускорение представляет собой сумму названных компонент, поэтому его вектор может быть направлен произвольным образом по отношению к линии окружности.
Если тело совершает вращение без изменения линейной скорости, то существует отличная от нуля только нормальная компонента, поэтому вектор полного ускорения направлен к центру окружности. Заметим, что к этому центру также действует сила, удерживающая тело на его траектории. Например, сила гравитации Солнца удерживает нашу Землю и другие планеты на своих орбитах.
Среднее и мгновенное ускорение и скорость. Формулы. Пример задачи
В физике рассмотрением особенностей движения макроскопических твердых тел занимается кинематика. Этот раздел механики оперирует такими понятиями, как скорость, ускорение и путь. В данной статье мы сосредоточим свое внимание на вопросах, что такое мгновенное ускорение и скорость. Также рассмотрим, какими формулами можно определить эти величины.
Нахождение скорости
Об этом понятии известно каждому школьнику, начиная уже с младших классов. Все ученики знакомы с приведенной ниже формулой:
В старших классах школ скорость, как физическая величина, рассматривается в новом свете. Ученикам предлагают следующее ее определение:
Ускорение
Благодаря этому равенству можно определить изменение величины v в любой точке траектории.
По аналогии со скоростью, среднее ускорение вычисляется по такой формуле:
Движение с постоянным ускорением
Отличительной особенностью этого типа перемещения тел в пространстве является постоянство величины а, то есть a=const.
Это движение также называют равноускоренным или равнозамедленным в зависимости от взаимного направления векторов скорости и ускорения. Ниже такое перемещение рассмотрим на примере двух наиболее распространенных траекторий: прямой линии и окружности.
При перемещении по прямой линии во время равноускоренного движения мгновенная скорость и ускорение, а также величина пройденного пути, связаны следующими равенствами:
Что касается скорости, то первое выражение позволяет определить ее в любой момент времени. То есть это будет мгновенный показатель. Для расчета средней скорости необходимо воспользоваться представленным выше выражением, то есть:
v = S/t = v0 ± a*(t1 + t2)/2.
При изучении движения по окружности с постоянным ускорением в физике используют угловые характеристики, которые аналогичны соответствующим линейным. К ним относится угол поворота θ, угловая скорость и ускорение (ω и α). Эти величины связаны в равенства, аналогичные выражениям равноускоренного движения по прямой линии, которые приводятся ниже:
При этом угловые характеристики связаны с линейными следующим образом:
Задача на определение среднего и мгновенного ускорения
Известно, что тело движется по сложной траектории. Его мгновенная скорость меняется по времени следующим образом:
Чему равно мгновенное ускорение тела в момент t=3 (секунды)? Найти среднее ускорение за промежуток времени от двух до четырех секунд.
На первый вопрос задачи ответить несложно, если вычислить производную от функции v(t). Получаем:
Для определения среднего ускорения, следует воспользоваться таким выражением:
Из расчетов следует, что среднее ускорение немного превышает мгновенное в середине рассмотренного временного промежутка.
Кинематика
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
2. по виду траектории
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где \( S \) — перемещение тела относительно неподвижной системы отсчета;
\( S_1 \) — перемещение тела относительно подвижной системы отсчета;
\( S_2 \) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где \( v \) — скорость тела относительно неподвижной системы отсчета;
\( v_1 \) — скорость тела относительно подвижной системы отсчета;
\( v_2 \) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_ <12>\) :
Определим скорость второго тела относительно первого \( v_ <21>\) :
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом \( \alpha \) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — \( v \) , единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
где \( v \) – конечная скорость; \( v_0 \) – начальная скорость;
\( t \) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где \( a_n \) – нормальное ускорение, \( a_ <\tau>\) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если \( a_ <\tau>\) ≠ 0, \( a_n \) = 0, то тело движется по прямой;
если \( a_ <\tau>\) = 0, \( a_n \) = 0, \( v \) ≠ 0, то тело движется равномерно по прямой;
если \( a_ <\tau>\) = 0, \( a_n \) ≠ 0, тело движется равномерно по кривой;
если \( a_ <\tau>\) = 0, \( a_n \) = const, то тело движется равномерно по окружности;
если \( a_ <\tau>\) ≠ 0, \( a_n \) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью \( t \) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \) , тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: \( x=x(t) \) .
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, \( a_x \) > 0.
График 2 лежит под осью t, тело тормозит, \( a_x \) \( v_ <0x>\) > 0, \( a_x \) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, \( v_ <0x>\) > 0, \( a_x \) \( v_ <0x>\) \( a_x \) \( t_2-t_1 \) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в \( n \) -ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то \( v_0 \) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то \( v \) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость \( v_0 \) , с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол \( \alpha \) , под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – \( T \) , единицы измерения – с.
где \( N \) – количество оборотов, \( t \) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – \( \nu \) , единицы измерения – с –1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – \( v \) , единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Мгновенная скорость нижней точки \( (m) \) равна нулю, мгновенная скорость в верхней точке \( (n) \) равна удвоенной скорости \( v_1 \) , мгновенная скорость точки \( (p) \) , лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке \( (c) \) – по теореме косинусов.