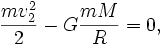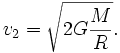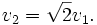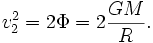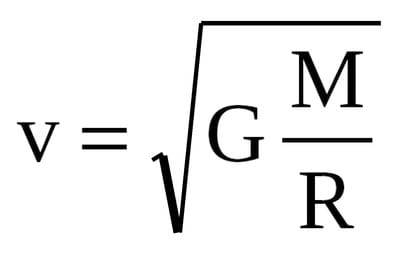что такое скорость убегания
Убегания скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела. Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
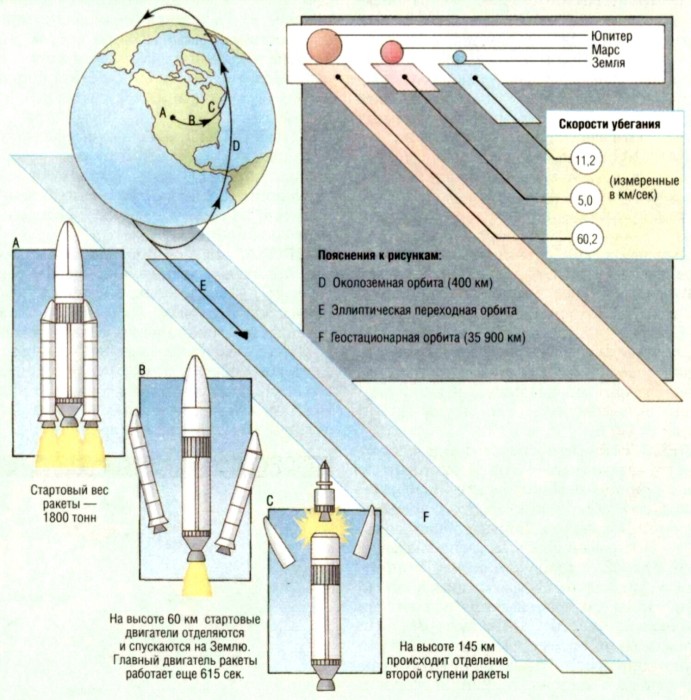
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.
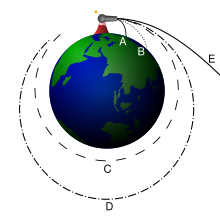
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Вывод формулы
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная, v2 — вторая космическая скорость.
Разрешая относительно v2, получим
Между первой и второй космическими скоростями существует простое соотношение:
Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности планеты):
См. также
Полезное
Смотреть что такое «Убегания скорость» в других словарях:
Убегания скорость — ускользания скорость, то же, что Вторая космическая скорость. Термин «У. с.» обычно применяется в астрофизике при описании явлений, связанных с движением молекул, составляющих атмосферы планет, звёзд и др. небесных тел … Большая советская энциклопедия
СКОРОСТЬ УБЕГАНИЯ — (вторая космическая скорость), минимальная скорость, необходимая для того, чтобы тело преодолело силу притяжения небесного тела или звездной системы. Скорость убегания для Земли равна 11,2 км/сек, для Луны 2,4 км/сек. Эту скорость можно вычислить … Научно-технический энциклопедический словарь
Скорость убегания — … Википедия
Ускользания скорость — в астрономии, см. Убегания скорость … Большая советская энциклопедия
Космическая скорость — (первая v1, вторая v2, третья v3 и четвёртая v4) это мин … Википедия
Космические скорости — первая, вторая, третья критические значения скорости летательного аппарта в момент его выхода на орбиту, определяющие форму траектории его движения в космическом пространстве. К. с. могут быть вычислены для любого расстояния r от центра Земли,… … Энциклопедия техники
космические скорости — первая, вторая, третья критические значения скорости летательного аппарта в момент его выхода на орбиту, определяющие форму траектории его движения в космическом пространстве. К. с. могут быть вычислены для любого расстояния r от центра… … Энциклопедия «Авиация»
космические скорости — первая, вторая, третья критические значения скорости летательного аппарта в момент его выхода на орбиту, определяющие форму траектории его движения в космическом пространстве. К. с. могут быть вычислены для любого расстояния r от центра… … Энциклопедия «Авиация»
СКОРОСТЬ УБЕГАНИЯ
Смотреть что такое «СКОРОСТЬ УБЕГАНИЯ» в других словарях:
Скорость убегания — … Википедия
Убегания скорость — ускользания скорость, то же, что Вторая космическая скорость. Термин «У. с.» обычно применяется в астрофизике при описании явлений, связанных с движением молекул, составляющих атмосферы планет, звёзд и др. небесных тел … Большая советская энциклопедия
Космическая скорость — (первая v1, вторая v2, третья v3 и четвёртая v4) это мин … Википедия
Ускользания скорость — в астрономии, см. Убегания скорость … Большая советская энциклопедия
ОРБИТА — в астрономии, путь небесного тела в пространстве. Хотя орбитой можно называть траекторию любого тела, обычно имеют в виду относительное движение взаимодействующих между собой тел: например, орбиты планет вокруг Солнца, спутников вокруг планеты… … Энциклопедия Кольера
Планеты — (позднелат., единственное число planeta, от греч. astèr planétes блуждающая звезда) большие небесные тела, движущиеся вокруг Солнца и светящиеся отраженным солнечным светом; размеры и массы П. на несколько порядков меньше, чем у Солнца.… … Большая советская энциклопедия
Эффект Оберта — Эффект Оберта в космонавтике эффект, проявляющийся в том, что ракетный двигатель, движущийся с высокой скоростью, создает больше полезной энергии, чем такой же двигатель, движущийся медленно. Эффект Оберта вызывается тем, что при… … Википедия
Космические скорости: насколько быстро нужно лететь, чтобы покинуть Землю, планетную систему и галактику?
Несмотря на то, что отечественная космонавтика переживает не лучшие, мягко говоря, времена, космосом на сегодняшний день интересуется все больше людей разного возраста и уровня образования. Усилиями частных инвесторов и популяризаторов науки пространство за пределами нашей планеты становится все более интересным, доступным и понятным, привлекая любознательных граждан к получению новых знаний.
В этом материале мы кратко, избегая сложных пояснений и формулировок, расскажем о космических скоростях, которые необходимы для преодоления гравитационных полей астрономических объектов. В новостных сюжетах мы часто слышим такое словосочетание, как «первая (вторая, третья, четвертая) космическая скорость», однако далеко не каждый обыватель понимает о каких скоростях идет речь и как их определяют.
Что такое космическая скорость
Космическими скоростями в космонавтике (речь идет не только о пилотируемых полетах, но для удобства мы будем называть все запуски искусственных космических аппаратов космонавтикой) пользуются для расчета минимально необходимой скорости для:
1. Выхода космических аппаратов на орбиту Земли;
2. Выхода космических аппаратов за пределы гравитационного поля Земли;
3. Выхода космических аппаратов за пределы Солнечной системы;
4. Выхода космических аппаратов за пределы галактики Млечный Путь.
Естественно, формулы расчета космических скоростей применимы не только к нашей планете, но и к любому другому объекту Вселенной, однако мы рассмотрим лишь актуальные для земных космических аппаратов значения.
Первая космическая скорость — 7,9 км/сек
Чтобы вращаться на орбите Земли, спутнику необходимо иметь первую космическую или круговую скорость, которая для нашей планеты равна примерно 7,9 км/сек. В этом случае объект на орбите будет удерживать сила, называемая в народе центробежной, а движение Земли и сила притяжения не позволят спутнику покинуть гравитационное поле планеты.
Отсюда следует довольно интересное и простое умозаключение: что будет если в формуле расчета первой космической скорости (V1 = (GM/R) в степени 1/2, где M — масса объекта, R — радиус, а G — гравитационная постоянная) поиграть с цифрами и подставить данные, которые определят первую космическую скорость для выдуманного нами объекта, как равную скорости света (чуть менее 300 000 км/сек)?
Мы получим объект огромной массы и малого радиуса, на который свет может падать, но покинуть его гравитационное поле фотоны уже не в состоянии, ведь для этого нужна вторая космическая скорость, которая в данном случае будет превышать скорость света, что невозможно в известной нам Вселенной. Это есть объект, о котором слышал каждый и который астрофизики называют «черной дырой».
Вторая космическая скорость — 11,2 км/сек
В 1959 году в СССР состоялся запуск автоматической межпланетной станции Луна-1 — первого искусственного объекта, покинувшего гравитационное поле Земли и ставшего спутником Солнца. Для этого аппарату пришлось разогнаться до второй космической скорости (она же скорость убегания), которая для Земли составляет порядка 11,2 км/сек. Покинув Землю на такой скорости, объект выходит на параболическую орбиту, которая при условии отсутствия других тел во Вселенной позволила бы ему бесконечно далеко удалиться от планеты.
Третья космическая скорость — 16,6 км/сек
Определить точное значение третьей космической скорости невозможно, так оно может колебаться в довольно широком диапазоне. Имеет значение угол направления запуска к траектории движения Земли по орбите и контакт с гравитационными полями других планет, которые могут как ускорять, так и притормаживать КА. Минимальное значение третьей космической скорости оценивается как 16,6 км/сек.
Четвертая космическая скорость — 400-600 км/сек
Редко употребляемый термин ввиду недосягаемости определяемых им величин для нашей космонавтики в обозримом будущем. Четвертая космическая скорость подразумевает вылет КА за пределы галактики, что в принципе невозможно при текущем и ожидаемом уровне развития технологий. Учитывая, что наша Солнечная система вращается вокруг галактического центра со скоростью около 220 км/сек, примерную расчетную скорость искусственного аппарата для вылета за пределы Млечного Пути можно определить как 400-600 км/сек.
Пожалуйста, оцените статью
Средняя оценка / 5. Количество оценок:
Оценок пока нет. Поставьте оценку первым.
Интересно, спасибо за статью)
А что же тогда, говорят, что Вояджер — первый, что покинуло СС
вообще-то размер СС составляет около 0,0015 световых лет.
Солнечная система не ограничена орбитами планет.
Вояджер разогнали до 42 км в сек. Для этого использовали удачное расположение тяжелых планет Юпитер, Сатурн, Нептун.
Вояджер уже был хорошо разогнан до Юпитера. И + притяжение Юпитера добавило скорости. Пролетаю около Юпитера по кривой, Вояджер был подхвачен Ураном или Сатурном. Точно не помню.
Говорят что кур доят, Вояджер всего лишь покинул сферу солнечного ветра
Сфера солнечного ветра — Нобелевскую премию за это определение, мужики-то не знали)))
Покинуть можно с любой скоростью, если будет постоянно работать двигатель.Это всё скорости свободного полёта, когда отключены двигатели.
А это вообще двоечник написал «В 2013 году Вояджер-1, преодолев более 18 млрд километров и набрав скорость около 17 км/сек»
не набрав 17 км/с, а потеряв до 17 км/с. Потому что в 1990 году Вояджер чесал больше 25 км/с, но постепенно замедляется притяжением Солнца.
То есть есть шанс что вояджеры вообще никуда не улетят и солнце замедлит их скорость удаления до нуля и притянет обратно?
Ракета, непрерывно ускоряемая за счет своего выхлопа, может улететь, никогда не достигнув космической скорости, поскольку она продолжает добавлять кинетическую энергию от своих двигателей. Он может совершить побег на любой скорости при наличии достаточного количества топлива, чтобы обеспечить новое ускорение ракете, противодействовать замедлению силы тяжести и, таким образом, сохранить ее скорость.
Для сферически-симметричного массивного тела, такого как звезда или планета, космическая скорость этого тела на заданном расстоянии рассчитывается по формуле
В этих уравнениях не учитывается атмосферное трение ( сопротивление воздуха ).
СОДЕРЖАНИЕ
Обзор
Существование космической скорости является следствием сохранения энергии и энергетического поля конечной глубины. Для объекта с заданной полной энергией, который движется под действием консервативных сил (таких как статическое гравитационное поле), объект может достигать только комбинаций местоположений и скоростей, которые имеют эту полную энергию; а места с более высокой потенциальной энергией, чем эта, вообще не могут быть достигнуты. Добавляя скорость (кинетическую энергию) к объекту, он расширяет возможные местоположения, которые могут быть достигнуты, до тех пор, пока при достаточной энергии они не станут бесконечными.
( K + U грамм ) я п я т я а л знак равно ( K + U грамм ) ж я п а л <\ Displaystyle (К + U_
Мы можем установить K ƒinal = 0, потому что конечная скорость произвольно мала, и U gƒinal = 0, потому что конечное расстояние равно бесконечности, поэтому
Сценарии
С поверхности тела
Альтернативное выражение для скорости убегания, особенно полезное на поверхности тела: v е <\ displaystyle v_
Для тела со сферически-симметричным распределением массы скорость убегания с поверхности пропорциональна радиусу, предполагающему постоянную плотность, и пропорциональна квадратному корню из средней плотности ρ. v е <\ displaystyle v_
Обратите внимание, что эта космическая скорость относится к невращающейся системе отсчета, а не к движущейся поверхности планеты или луны, как мы сейчас объясняем.
Из вращающегося тела
Практические соображения
Из орбитального тела
Барицентрическая убегающая скорость
Технически космическая скорость может быть измерена либо относительно другого, центрального тела, либо относительно центра масс или центра масс системы тел. Таким образом, для систем из двух тел термин « космическая скорость» может быть неоднозначным, но обычно он означает барицентрическую космическую скорость менее массивного тела. В гравитационных полях скорость убегания относится к скорости убегания пробных частиц с нулевой массой относительно центра масс, генерирующих поле. В большинстве ситуаций, связанных с космическими кораблями, разница незначительна. Для массы, равной ракете Сатурн V, космическая скорость относительно стартовой площадки на 253,5 ам / с (8 нанометров в год) больше, чем космическая скорость относительно взаимного центра масс.
Высота низкоскоростных траекторий
что, решение для h приводит к
В отличие от скорости убегания, направление (вертикально вверх) важно для достижения максимальной высоты.
Траектория
Если тело имеет скорость, превышающую скорость убегания, то его путь будет формировать гиперболическую траекторию, и у него будет избыточная гиперболическая скорость, эквивалентная дополнительной энергии, имеющейся у тела. Относительно небольшая дополнительная дельта- v выше, необходимая для ускорения до аварийной скорости, может привести к относительно большой скорости на бесконечности. Некоторые орбитальные маневры используют этот факт. Например, в месте, где скорость эвакуации составляет 11,2 км / с, прибавление 0,4 км / с дает гиперболическую избыточную скорость 3,02 км / с:
Если тело на круговой орбите (или в перицентре эллиптической орбиты) ускоряется в направлении своего движения до скорости убегания, точка ускорения будет формировать перицентр траектории ухода. Возможное направление движения будет под углом 90 градусов к направлению точки ускорения. Если тело разгоняется до скорости, превышающей скорость убегания, конечное направление движения будет под меньшим углом и обозначено одной из асимптот гиперболической траектории, которую оно сейчас принимает. Это означает, что время ускорения имеет решающее значение, если намерение состоит в том, чтобы уйти в определенном направлении.
Скорость будет асимптотически приближаться
Список скоростей убегания
| Место нахождения | Относительно | V e (км / с) | Место нахождения | Относительно | V e (км / с) | Система эвакуации, V te (км / с) |
|---|---|---|---|---|---|---|
| На солнце | Гравитация Солнца | 617,5 | ||||
| На Меркурии | Гравитация Меркурия | 4,25 | На Меркурии | Гравитация Солнца | ||
| На Венере | Гравитация Венеры | 10,36 | На Венере | Гравитация Солнца | 49,5 | 17,8 |
| На Земле | Земное притяжение | 11,186 | На Земле | Гравитация Солнца | 42,1 | 16,6 |
| На Луне | Гравитация Луны | 2.38 | На Луне | Гравитация Земли | 1.4 | 2,42 |
| На марсе | Гравитация Марса | 5,03 | На Марсе | Гравитация Солнца | 34,1 | 11.2 |
| На Церере | Гравитация Цереры | 0,51 | На Церере | Гравитация Солнца | 25,3 | 7,4 |
| На Юпитере | Гравитация Юпитера | 60,20 | На Юпитере | Гравитация Солнца | 18,5 | 60,4 |
| На Ио | Гравитация Ио | 2,558 | На Ио | Гравитация Юпитера | 24,5 | 7,6 |
| На европе | Гравитация Европы | 2,025 | В Европе | Гравитация Юпитера | 19,4 | 6.0 |
| На Ганимеде | Гравитация Ганимеда | 2,741 | На Ганимеде | Гравитация Юпитера | 15.4 | 5,3 |
| О Каллисто | Гравитация Каллисто | 2,440 | В Каллисто | Гравитация Юпитера | 11,6 | 4.2 |
| На Сатурне | Гравитация Сатурна | 36,09 | На Сатурне | Гравитация Солнца | 13,6 | 36,3 |
| На Титане | Гравитация Титана | 2,639 | На Титане | Гравитация Сатурна | 7,8 | 3.5 |
| На Уране | Гравитация Урана | 21,38 | На Уране | Гравитация Солнца | 9,6 | 21,5 |
| На нептуне | Гравитация Нептуна | 23,56 | На Нептуне | Гравитация Солнца | 7,7 | 23,7 |
| На Тритоне | Гравитация Тритона | 1,455 | В Тритоне | Гравитация Нептуна | 6.2 | 2.33 |
| На Плутоне | Гравитация Плутона | 1,23 | На Плутоне | Гравитация Солнца | ||
| В галактическом радиусе Солнечной системы | Млечный Путь гравитация s | 492–594 | ||||
| На горизонте событий | А черная дыра «гравитационное | 299 792,458 ( скорость света ) |
Последние два столбца будут точно зависеть от того, где на орбите достигается космическая скорость, поскольку орбиты не совсем круговые (особенно Меркурий и Плутон).
Получение скорости убегания с помощью исчисления
Поэтому работа, необходимая для перемещения тела на небольшое расстояние dr против этой силы, определяется выражением
Тогда общая работа, необходимая для перемещения тела с поверхности r 0 гравитирующего тела на бесконечность, равна
Чтобы выполнить эту работу, чтобы достичь бесконечности, минимальная кинетическая энергия тела при вылете должна соответствовать этой работе, поэтому скорость убегания v 0 удовлетворяет
Параболическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела. Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Вывод формулы
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная, v2 — вторая космическая скорость.
Разрешая относительно v2, получим
Между первой и второй космическими скоростями существует простое соотношение:
Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности планеты):
См. также
Полезное
Смотреть что такое «Параболическая скорость» в других словарях:
ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ — минимальная скорость, которую нужно сообщить телу массой m (напр., космическому аппарату), чтобы оно могло преодолеть гравитационное притяжение другого тела массой М m (напр., Земли) и, двигаясь по параболической траектории, навсегда покинуть… … Большой Энциклопедический словарь
ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ — см. Космическиескорости. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия
параболическая скорость — минимальная скорость, которую нужно сообщить телу массой т (например, космическому аппарату), чтобы оно могло преодолеть гравитационное притяжение другого тела массой М>>т (например, Земли) и, двигаясь по параболической траектории, навсегда… … Энциклопедический словарь
параболическая скорость — parabolinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Paraboline trajektorija judančio taško ar kūno greitis. atitikmenys: angl. parabolic velocity vok. parabolische Geschwindigkeit, f rus. параболическая скорость, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
параболическая скорость — parabolinis greitis statusas T sritis fizika atitikmenys: angl. parabolic velocity vok. parabolische Geschwindigkeit, f rus. параболическая скорость, f pranc. vitesse parabolique, f … Fizikos terminų žodynas
Параболическая скорость — скорость, которую нужно сообщить тому или иному телу (космическому зонду, частице атмосферы и т.п.), чтобы оно, преодолев притяжение Земли (Луны, планеты и др.), удалилось от неё по параболической орбите. П. с. уменьшается с расстоянием… … Большая советская энциклопедия
Параболическая скорость — тело, движущееся по параболе, в каждой точке своей орбиты имеет скорость, квадрат которой в два раза больше квадрата скорости тела движущегося по кругу, около того же центра притяжения, проходящего через эту точку. Это следует из так наз. закона… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ — миним. скорость, к рую нужно сообщить телу мяссой т (напр., космич. аппарату), чтобы оно могло преодолеть гравитац. притяжение др. тела массой Мт>> (напр., Земли) и, двигаясь по параболич. траектории, навсегда покинуть сферу его гравитац.… … Естествознание. Энциклопедический словарь
ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ — см. Космические скорости … Большой энциклопедический политехнический словарь
Орбитальная скорость — … Википедия