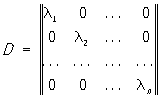что такое симметричная матрица

16.12.202327.09.2023 admin 0 Comments

Симметричная матрица

Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали. Более формально, симметричной называют такую матрицу , что .

Это означает, что она равна её транспонированной матрице:

Примеры

Свойства

Симметричная матрица всегда квадратная.

Для любой симметричной матрицы A с вещественными элементами справедливо следующее:

Полезное

Смотреть что такое «Симметричная матрица» в других словарях:

Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия

Матрица моментов плана — 47. Матрица моментов плана Квадратичная симметричная матрица, элементы которой есть скалярные произведения соответствующих векторов столбцов матрицы базисных функций Источник: ГОСТ 24026 80: Исследовательские испытания. Планирование эксперимента … Словарь-справочник терминов нормативно-технической документации

МАТРИЦА — прямоугольная таблица состоящая из т строк и n столбцов; её паз. M. размера Элементами(первый индекс указывает номер строки, второй номер столбца) M. могут быть числа, ф ции пли др. величины, над к рыми можно производить алгебраич. операции. M.… … Физическая энциклопедия

Матрица (в математике) — Матрица в математике, система элементов aij (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы. Если схема имеет m строк и n столбцов, то говорят о (m n) матрице.… … Большая советская энциклопедия

Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия

Матрица — I Матрица (нем. Matrize, от латинского matrix матка, источник, начало) в полиграфии, 1) сменный элемент литейной формы с углублённым (иногда фотографическим) изображением буквы или знака, используемый при отливке типографских… … Большая советская энциклопедия

матрица пучка Р — 3.8 матрица пучка Р: Симметричная, положительно определенная 4×4 матрица, содержащая все десять моментов второго порядка вигнеровского распределения и его элементов; записывается следующим образом: (7)… … Словарь-справочник терминов нормативно-технической документации

Квадратная матрица — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия

Обратная матрица — Обратная матрица такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для… … Википедия

Источник

В линейная алгебра, а симметричная матрица это квадратная матрица что равно его транспонировать. Формально,

Поскольку одинаковые матрицы имеют одинаковые размеры, симметричными могут быть только квадратные матрицы.

Каждый квадрат диагональная матрица симметрично, так как все недиагональные элементы равны нулю. Аналогично в характеристика отличается от 2, каждый диагональный элемент кососимметричная матрица должен быть равен нулю, так как каждое из них является отрицательным.

Содержание

пример

Свойства

Основные свойства

Разложение на симметричные и кососимметричные

Матрица, конгруэнтная симметричной матрице

Симметрия подразумевает нормальность

(Действительная) симметричная матрица обязательно является нормальная матрица.

Действительные симметричные матрицы

Комплексные симметричные матрицы

Разложение

С использованием Нормальная форма Джордана, можно доказать, что каждая квадратная вещественная матрица может быть записана как произведение двух действительных симметричных матриц, а каждая квадратная комплексная матрица может быть записана как произведение двух комплексных симметричных матриц. [4]

Каждый настоящий невырожденная матрица можно однозначно рассматривать как результат ортогональная матрица и симметричный положительно определенная матрица, который называется полярное разложение. Сингулярные матрицы также можно разложить на множители, но не однозначно.

Сложная симметричная матрица не может быть диагонализована по подобию; каждая вещественная симметричная матрица диагонализуема действительным ортогональным подобием.

Гессен

с реальными числами λ я < displaystyle lambda _ > . Это значительно упрощает изучение квадратичных форм, а также изучение множеств уровней. < Икс : q ( Икс ) = 1 >< displaystyle left < mathbf : q ( mathbf ) = 1 right >> которые являются обобщениями конические секции.

Это важно отчасти потому, что поведение второго порядка каждой гладкой функции с несколькими переменными описывается квадратичной формой, принадлежащей гессиану функции; это следствие Теорема Тейлора.

Симметризуемая матрица

Смотрите также

Другие виды симметрия или узоры в квадратных матрицах имеют специальные названия; см. например:

Источник

Симметрическая матрица

Смотреть что такое «Симметрическая матрица» в других словарях:

СИММЕТРИЧЕСКАЯ МАТРИЦА — квадратная матрица … Большой Энциклопедический словарь

симметрическая матрица — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN symmetric matrix … Справочник технического переводчика

симметрическая матрица — квадратная матрица aik, в которой любые два элемента, симметрично расположенные относительно главной диагонали, равны между собой: aik=aki. * * * СИММЕТРИЧЕСКАЯ МАТРИЦА СИММЕТРИЧЕСКАЯ МАТРИЦА, квадратная матрица ||aik||, в которой любые два… … Энциклопедический словарь

симметрическая матрица — simetrinė matrica statusas T sritis fizika atitikmenys: angl. symmetric matrix; symmetrical matrix vok. symmetrische Matrix, f rus. симметрическая матрица, f pranc. matrice symétrique, f … Fizikos terminų žodynas

СИММЕТРИЧЕСКАЯ МАТРИЦА — квадратная матрица од, в к рой любые два элемента, симметрично расположенные относительно главной диагонали, равны между собой: аik = аki … Естествознание. Энциклопедический словарь

Матрица Гессе — Гессиан функции симметрическая квадратичная форма описывающая поведение функции во втором порядке. Для функции f дважды дифференцируемой в точке или где (или … Википедия

Самосопряжённая матрица — (математическая) Матрица, совпадающая со своей сопряжённой, т. е. такая, что aik = где число, комплексно сопряжённое с а. Если элементы С. м. действительны, то она симметрическая (см. Симметрическая матрица). С. м. имеет действительные… … Большая советская энциклопедия

Ковариационная матрица — (или матрица ковариаций) в теории вероятностей это матрица, составленная из попарных ковариаций элементов одного или двух случайных векторов. Ковариационная матрица случайного вектора квадратная симметрическая матрица, на диагонали… … Википедия

Источник

Инструменты сайта

Основное

Информация

Действия

Содержание

Матрица

Определение, обозначения

(количество строк, количество столбцов)

Пример.

Элементарные операции

умножение на число

сложение

транспонирование

Показать справедливость следующих свойств операции транспонирования:

при условии, что все операции в левых частях равенств определены (операция умножения матриц определяется ☟ НИЖЕ ).

конкатенация

векторизация

перезагрузка

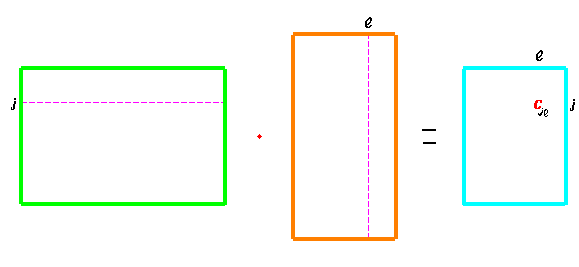
Умножение матриц

В схематичном виде:

Пример.

Доказательство ☞ ЗДЕСЬ.

Что послужило причиной введения такой операции умножения?

Ответ и дальнейшие свойства операции умножения ☞ ЗДЕСЬ.

Квадратные матрицы

Пример.

симметричная

Подробнее о симметричной матрице ☞ ЗДЕСЬ.

единичная

кососимметричная

Указать все элементы кососимметричной матрицы

Свойства кососимметричной матрицы ☞ ЗДЕСЬ

обратно симметричная матрица

Пример.

треугольная

Хессенберга

Следующий класс матриц не относится ко множеству ортогональных, но близок к нему по смыслу.

Пример. Матрицы

Применение матрицы Адамара :

ганкелева

Подробнее о ганкелевой матрице ☞ ЗДЕСЬ.

тёплицева

Подробнее о циклической матрице ☞ ЗДЕСЬ

положительная

стохастическая

Пример.

Используется в теории вероятностей (цепи Маркова).

элементарных преобразований

Матрицы элементарных преобразований используются при анализе метода Гаусса решения систем линейных уравнений.

ленточная

Ленточные матрицы возникают в численных методах решения граничных задач для обыкновенных дифференциальных уравнений; см. ☞ МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ.

Часто встречающиеся («именные») матрицы

Вандермонда

$$ \mathbf V(x_1,\dots,x_n)= \left[ x_j^ \right]_^= \left(\begin 1 &x_1&x_1^2&\ldots&x_1^\\ 1 &x_2&x_2^2&\ldots&x_2^\\ \vdots& &&& \vdots\\ 1 &x_n&x_n^2&\ldots&x_n^ \end\right)_ $$ или ей транспонированная. Иногда рассматривают неквадратные матрицы Вандермонда.

Подробнее о матрице Вандермонда ☞ ЗДЕСЬ.

Свойства матрицы дискретного преобразования Фурье ☞ ЗДЕСЬ; ее применение ☞ ТРИГОНОМЕТРИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ.

Гессе

Подробнее о применениях матрицы Гессе к задачам исследования стационарных точек функции на экстремум, а также самой функции на выпуклость ☞ ЗДЕСЬ.

Грама

Подробнее о свойствах матрицы Грама и ее применении к задачам вычисления расстояний ☞ ЗДЕСЬ.

Фробениуса

Якоби

Применение матрицы Якоби ☞ ЗДЕСЬ

Функции от матрицы

определитель

Определение, свойства и применения определителя ☞ ЗДЕСЬ

характеристический полином

Структура, свойства и методы вычисления характеристического полинома ☞ ЗДЕСЬ

Методы вычисления, свойства и применения ранга матрицы ☞ ЗДЕСЬ

норма

Норма вводится не только для квадратных матриц. Подробнее ☞ ЗДЕСЬ.

Обращение матрицы

Показать справедливость следующих свойств операции обращения :

Предполагается, что в левой части каждого равенства операции определены.

Методы вычисления, свойства и применения обратной матрицы ☞ ЗДЕСЬ

Полином от матрицы и матричный полином

Проверить, что для матрицы из предыдущего примера, любая ее степень

Пример.

Матричные уравнения

Уравнение Ляпунова

Имеет важное значение в теории управления.

Далее идет сложный для понимания материал!

Квадратные уравнения

Матрица квадратичной формы

Матрица преобразования координат

Матрица линейного отображения

Источник

Поскольку одинаковые матрицы имеют одинаковые размеры, симметричными могут быть только квадратные матрицы.

Содержание

пример