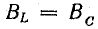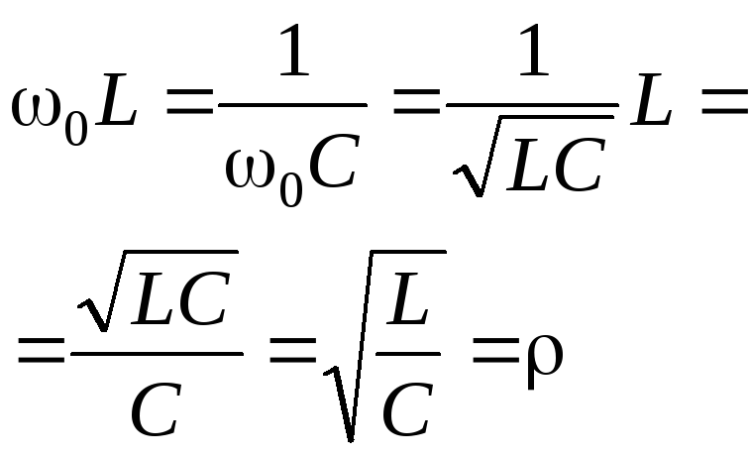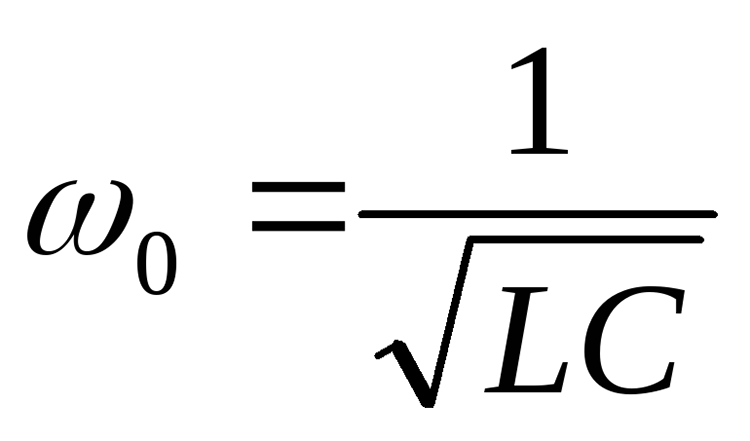что такое резонанс колебательного контура

Что такое резонанс колебательного контура

Свободные (или собственные) колебания — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие).

,

Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора EC = 0. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна

,

где L — индуктивность катушки, I0 — максимальное значение тока.

В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.

Рис 1. Пример: Осциллограмма LC контура во время замыкания заряженного конденсатора на катушку индуктивности.
С = 240нФ(заряженный), L = 360нГн, F0 ≈ 542кГц.

1.4.2. Вынужденные колебания в контуре.

Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:

.

Консервативный гармонический осциллятор

Второй закон Ньютона для такого осциллятора запишется в виде:

.

Если ввести обозначения:

,

и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:

,

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:

,

Найдём частное решение. Для этого подставим в уравнение решение вида:

,

и получим значение для константы:

,

Тогда окончательное решение запишется в виде:

.

1.4.3. Резонанс в колебательном контуре.

Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы.

В результате резонанса при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

При достижении резонанса, импеданс (комплексное сопротивление двухполюсника (электрической цепи, содержащей две точки для соединения с другими цепями) для гармонического сигнала) последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

,

f — резонансная частота в герцах;

L — индуктивность в генри;

C — ёмкость в фарадах.

Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы (параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.).

Рис 2. Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания.

1.4.4. Связанные цепи.

Если изменение тока в одном из элементов цепи приводит к появлению э.д.с. в другом элементе, то эти два элемента индуктивно связаны, а возникающая э.д.с. называется э.д.с. взаимной индукции.

Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи

,

где М – взаимная индуктивность элементов цепи,

При расчете цепей с взаимной индуктивностью следует на схеме отметить стрелками выбираемые положительные направления токов в ветвях (или контурных токов). Кроме того, одинаковыми условными значками (звездочками, точками, буквами и т.п.) обозначить одноименные зажимы каждой пары индуктивно связанных катушек.

Одноименными называются такие зажимы, при одинаковом положительном направлении токов относительно которых, магнитные потоки самоиндукции и взаимной индукции складываются.

1.4.5. Кварцевый резонатор.

Кварцевый резонатор — прибор, в котором пьезоэлектрический эффект и явление механического резонанса используются для построения высокодобротного резонансного элемента электронной схемы.

На пластинку, кольцо или брусок, вырезанные из кристалла кварца определённым образом, нанесены 2 и более электродов — проводящие полоски.

Пластинка закреплена и имеет собственную резонансную частоту механических колебаний.

При подаче напряжения на электроды благодаря пьезоэлектрическому эффекту происходит изгибание, сжатие или сдвиг в зависимости от того, каким образом вырезан кусок кристалла.

Однако колеблющаяся пластинка в результате того же пьезоэлектрического эффекта создаёт во внешней цепи противо-ЭДС, что можно рассматривать как явление, эквивалентное работе катушки индуктивности в колебательном контуре.

Если частота подаваемого напряжения равна или близка к частоте собственных механических колебаний пластинки, затраты энергии на поддержание колебаний пластинки оказываются намного ниже, нежели при большом отличии частоты. Это тоже соответствует поведению колебательного контура.

Рис 3. Эквивалентная схема.

Условное обозначение кварцевого резонатора (сверху) и его эквивалентная схема (снизу)

C0 — собственная ёмкость кристалла, образуемая кристаллодержателем и/или обкладками резонатора.

C1, L1 — эквивалентная ёмкость и индуктивность механической колебательной системы резонатора.

R1 — эквивалентное сопротивление потерь механической колебательной системы.

Источник

Резонанс напряжений в последовательном колебательном контуре

В радиотехнике широкое применение имеют электрические цепи, составленные из катушки индуктивности и конденсатора. Такие цепи в радиотехнике называются колебательными контурами. Источник переменного тока к колебательному контуру может быть присоединен двумя способами: последовательно (рисунок 1а) и параллельно (рисунок 1б).

Рисунок 1. Схемотическое обозначение колебательного контура. а) последовательный колебательный контур; б) параллельный колебательный контур.

Рассмотрим поведение колебательного контура в цепи переменного тока при последовательном соединении контура и источника тока (рис 1а).

Мы знаем, что такая цепь оказывает переменному току реактивное сопротивление, равное:

где R_L— активное сопротивление катушки индуктивности в ом;

ωL,-индуктивное сопротивление катушки индуктивности в ом;

1/ωC-емкостное сопротивление конденсатора в ом.

Активное сопротивление катушки R_L практически очень мало изменяется при изменении частоты (если пренебречь поверхностным эффектом). Индуктивное и емкостное сопротивления в очень сильной степени зависят от частоты, а именно: индуктивное сопротивление ωL увеличивается прямо пропорционально частоте тока, а емкостное сопротивление 1/ωC уменьшается при повышении частоты тока, т. е. оно связано с частотой тока обратно пропорциональной зависимостью.

Отсюда непосредственно следует, что реактивное сопротивление последовательного колебательного контура также зависит от частоты, и колебательный контур будет оказывать токам разных частот неодинаковое сопротивление.

Если мы будем измерять реактивное сопротивление колебательного контура при различных частотах, то обнаружим, что в области низких частот сопротивление последовательного контура очень велико; при увеличении частоты оно уменьшается до некоторого предела, а затем начинает снова возрастать.

Объясняется это тем, что в области низких частот ток испытывает большое сопротивление со стороны конденсатора, при увеличении же частоты начинает действовать индуктивное сопротивление, компенсирующее действие емкостного сопротивления.

При некоторой частоте индуктивное сопротивление становится равным емкостному, т. е.

Они будут взаимно компенсировать друг друга и общее реактивное сопротивление контура станет равным нулю:

При этом реактивное сопротивление последовательного колебательного контура будет равно только его активному сопротивлению, так как

При дальнейшем повышении частоты ток будет испытывать все большее и большее сопротивление со стороны индуктивности катушки, при одновременном уменьшении компенсирующего действия емкостного сопротивления. Поэтому реактивное сопротивление контура начнет снова возрастать.

На рисунке 2а приведена кривая, показывающая изменение реактивного сопротивления последовательного колебательного контура при изменении частоты тока.

Рисунок 2. Резонанс напряжений. а) зависимость изменения полного сопротивления от частоты; б) зависимость реактивного сопротивления от активного сопротивления контура; в) кривые резонанаса.

Частота тока, при которой сопротивление колебательного контура делается наименьшим, называется частотой резонанса или резонансной частотой колебательного контура.

При резонансной частоте имеет место равенство:

пользуясь которым, нетрудно определить частоту резонанса:

(1)

Единицами в этих формулах служат герцы, генри и фарады.

Из формулы (1) видно, что чем меньше величины емкости и самоиндукции колебательного контура, тем больше будет его резонансная частота.

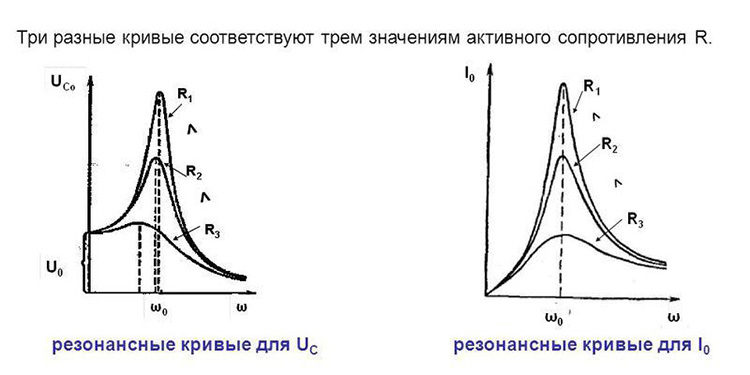
Величина активного сопротивления R_L не влияет на резонансную частоту, однако от нее зависит характер изменения Z. На рисунке 2б приведен ряд графиков изменения реактивного сопротивления колебательного контура при одних и тех же величинах L и С, но при разных R_L. Из этого рисунка видно, что чем больше активное сопротивление последовательного колебательного контура, тем тупее становится кривая изменения реактивного сопротивления.

Теперь рассмотрим, как будет изменяться сила тока в колебательном контуре, если мы будем изменять частоту тока. При этом мы будем считать, что напряжение, развиваемое источником переменного тока, остается все время одним и тем же.

Так как источник тока включен последовательно с L и С контура, то сила тока, протекающего через катушку и конденсатор, будет тем больше, чем меньше реактивное сопротивление колебательного контура в целом, так как

Отсюда непосредственно следует, что при резонансе сила тока в колебательном контуре будет наибольшей. Величина тока при резонансе будет зависеть от напряжения источника переменного тока и от активного сопротивления контура:

На рисунке 2г изображен ряд графиков изменения силы тока в последовательном колебательном контуре при изменении частоты тока так называемых кривых резонанса. Из этого рисунка видно, что чем больше активное сопротивление контура, тем тупее кривая резонанса.

При резонансе сила тока может достигать огромных значений при сравнительно малой внешней ЭДС. Поэтому падения напряжения на индуктивном и емкостном сопротивлениях контура, т. е. на катушке и на конденсаторе, могут достигать очень больших величии и далеко превосходить величину внешнего напряжения.

Последнее утверждение на первый взгляд может показаться несколько странным, однако нужно помнить, что фазы напряжений на емкостном и индуктивном сопротивлениях сдвинуты друг относительно друга на 180°, т. е. мгновенные значения напряжений на катушке и конденсаторе направлены всегда в противоположные стороны. Вследствие этого большие напряжения, существующие при резонансе внутри контура на его катушке и конденсаторе, ничем не обнаруживают себя вне контура, взаимно компенсируя друг друга.

Разобранный нами случай последовательного резонанса называется резонансом напряжений, так как в этом случае в момент резонанса имеет место резкое увеличение напряжения на L и С колебательного контура.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник

Колебательный контур: принцип работы, виды контуров, параметры и характеристики

Частота собственных колебаний контура (ее еще называют резонансной частотой fp ) зависит от индуктивности катушки и емкости конденсатора и вычисляется по формуле Томсона из которой видно, что чем меньше значения емкости и индуктивности, тем выше собственная частота контура:

Можно определить индуктивность или емкость контура по известной частоте fp:

L=253•10 2 /f 2 p•C; C=253•10 2 /f 2 p•L.

Последовательный колебательный контур

Так как в катушке и конденсаторе напряжения сдвинуты относительно тока на разные фазовые углы, то более наглядно их можно показать на векторных диаграммах ( рис.4 )

Как видно из диаграммы рис.4а при UL > Uc напряжение внешнего источника опережает ток в колебательном контуре на угол φ и находится выше оси абcцисс в зоне напряжений индуктивности. Значит в данном случае контур имеет сопротивление индуктивного характера.
При UL ( рис.4b ) вектор источника уже будет отставать от вектора тока на угол φ и контур будет иметь емкостное сопротивление.

Полное сопротивление контура Z будет равно:

Амплитудное значение тока Im определяется по формуле:

При выполнении равенства:

На рис.5 показан график характеристик зависимости тока Iк и полного сопротивления Z последовательного контура от частоты.

При резонансе амплитуда тока в контуре равна:

При резонансе отношение между напряжением на индуктивном сопротивлении и напряжением источника будет равно добротности Q катушки:
А добротность контуров, применяемых в радиотехнике, большая. Поэтому напряжение на катушке может превышать в сотни раз напряжение источника.
Но так как при резонансе напряжение на катушке равно напряжению на конденсаторе, значит отношение напряжения на конденсаторе к напряжению источника тоже будет равно добротности:

Для примера на рис.8 показана схема последовательного контура с реальными значениями элементов схемы и параметров, а так же полученные величины напряжений на этих элементах. Отсюда видно, что напряжение на катушке и конденсатотре при резонансе будет больше напряжения источника в Q раз.

Резонанс в последовательном колебательном контуром называют резонансом напряжения, т.к. напряжение на реактивных элементах при резонансе становится больше напряжения внешнего источника.

Полосой пропускания контура называют полосу частот, в пределах которой ток в контуре уменьшается не более, чем в заданное число раз по сравнению с током при резонансе ( рис.10 ):

Параллельный колебательный контур

В параллельном колебательном контуре источник сигнала соединен с катушкой индуктивности и конденсатором параллельно (рис.11).
При подаче переменного напряжения на контур происходит обмен энергиями между конденсатором и катушкой, но только в цепи внутри контура.

Для возникновения резонанса в нем, как и в последовательном контуре, необходимыми условиями являются равенство емкостного Хс и индуктивного ХL сопротивлений, а так же равенство частоты собственных колебаний контура и частоты колебаний источника тока.
Только резонанс в параллельном колебательном контуром, в отличии от резонанса в последовательном контуре, называют резонансом тока.

На рис.15 показан график характеристик зависимости тока Iк и полного сопротивления Z параллельного контура от частоты.

но он потребляет малый ток от источника, который необходим лишь для компенсации потерь в контуре:

Добротность Q параллельного контура, в отличии от последовательного контура, показывает во сколько раз ток в элементах контура больше потребления тока источника:

На рис.16 дан конкретный пример параллельного колебательного контура, где видно, что ток контура больше тока источника в Q раз.

В радиоприемниках так же применяется непосредственная связь колебательного контура с антенной, т.е. контур включен параллельно источнику сигнала ( рис.17 ).
Переменным конденсатором настраиваем контур на частоту сигнала нужной радиостанции. При резонансе контурный ток, вызванный нужной радиостанцией, становится относительно большим, а сопротивление контура тоже большим.Поэтому между точками а и b получается значительное напряжение.
Для других станций контур представляет малое сопротивление и сигнал радиостанции уходит в «землю».

Источник

Особенности резонанса токов

Что это такое

Резонанс токов — разновидность состояния электрической цепи, когда общий вид токовых показателей совпадает по фазам уровню напряжения, а мощность реактивного вида равна нулю или же она представлена в активном виде.

. Резонанс токов

Этот вариант развития событий характерен для переменного тока и имеет не только положительные свойства, но и некоторые нежелательные последствия. Так, благодаря резонансу работает радиотехника, автоматика и проволочная телефония, но в то же время возникают перенапряжения и сбои в работе электрической системы.

Определение из учебного пособия

При каких условиях возникает

Условием того, чтобы возникло это явление, является равные показатели проводниковой частоты, где BL=BC. То есть емкостная с индуктивной проводимостью должна быть равна. Только тогда подобное явление резонанса токов наблюдается в электрической цепи. Он при этом может быть как положительным, так и отрицательным. В любом радиоприемнике есть колебательный контур, который из-за индуктивного или емкостного изменения, настраивается на нужный сигнал радиоволны. В другом случае, это ведет к тому, что появляются скачки напряжения или ток в цепи и появляется аварийная ситуация.

В условиях лаборатории, он возникает во время, когда изменяется емкость и не изменяется индуктивность катушки L. В таком случае формула выглядит как Bc=C

При каких условиях возникает

Что такое резонанс?

Определение явления по ТОЭ: электрический резонанс происходит в электрической цепи при определенной резонансной частоте, когда некоторые части сопротивлений или проводимостей элементов схемы компенсируют друг друга. В некоторых схемах это происходит, когда импеданс между входом и выходом схемы почти равен нулю, и функция передачи сигнала близка к единице. При этом очень важна добротность данного контура.

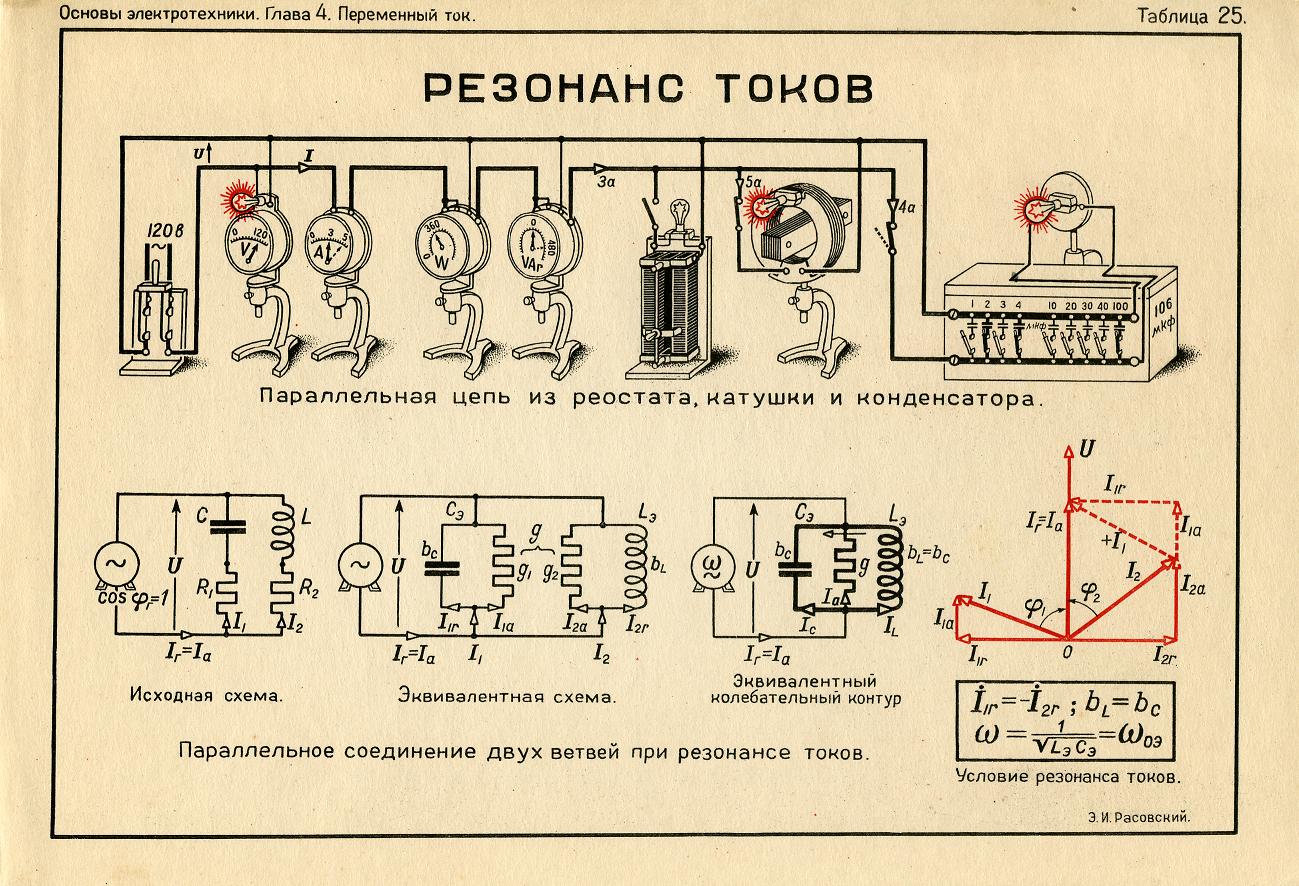
Соединение двух ветвей при резонансе

Иными словами, резонанс в цепи переменного тока подразумевает специальную частоту, и определяется значениями сопротивления, емкости и индуктивности. Существует два типа резонанса токов:

Для последовательного резонанса условие является простым и характеризуется минимальным сопротивлением и нулевой фазе, он используется в реактивных схемах, также его применяет разветвленная цепь. Параллельный резонанс или понятие RLC-контура происходит, когда индуктивные и емкостные данные равны по величине, но компенсируют друг друга, так как они находятся под углом 180 градусов друг от друга. Это соединение должно быть постоянно равным указанной величине. Он получил более широкое практическое применение. Резкий минимум импеданса, который ему свойствен, является полезным для многих электрических бытовых приборов. Резкость минимума зависит от величины сопротивления.

Схема RLC (или контур) является электрической схемой, которая состоит из резистора, катушки индуктивности, и конденсатора, соединенных последовательно или параллельно. Параллельный колебательный контур RLC получил свое название из-за аббревиатуры физических величин, представляющих собой соответственно сопротивление, индуктивность и емкость. Схема образует гармонический осциллятор для тока. Любое колебание индуцированного в цепи тока, затухает с течением времени, если движение направленных частиц, прекращается источником. Этот эффект резистора называется затуханием. Наличие сопротивления также уменьшает пиковую резонансную частоту. Некоторые сопротивление являются неизбежными в реальных схемах, даже если резистор не включен в схему.

Применение

Практически вся силовая электротехника использует именно такой колебательный контур, скажем, силовой трансформатор. Также схема необходима для настройки работы телевизора, емкостного генератора, сварочного аппарата, радиоприемника, её применяет технология «согласование» антенн телевещания, где нужно выбрать узкий диапазон частот некоторых используемых волн. Схема RLC может быть использована в качестве полосового, режекторного фильтра, для датчиков для распределения нижних или верхних частот.

Резонанс даже использует эстетическая медицина (микротоковая терапия), и биорезонансная диагностика.

Принцип резонанса токов

Мы можем сделать резонансную или колебательную схему в собственной частоте, скажем, для питания конденсатора, как демонстрирует следующая диаграмма:

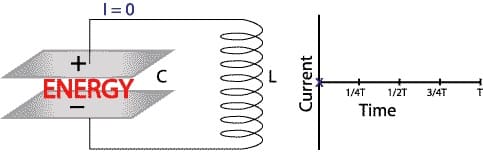
Схема для питания конденсатора

Переключатель будет отвечать за направление колебаний.

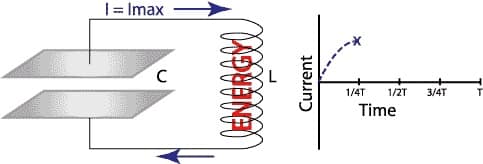
Схема: переключатель резонансной схемы

Конденсатор сохраняет весь ток в тот момент, когда время = 0. Колебания в цепи измеряются при помощи амперметров.

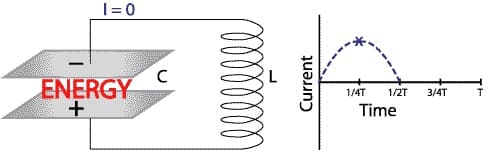
Схема: ток в резонансной схеме равен нулю

Направленные частицы перемещаются в правую сторону. Катушка индуктивности принимает ток из конденсатора.

Когда полярность схемы приобретает первоначальный вид, ток снова возвращается в теплообменный аппарат.

Теперь направленная энергия снова переходит в конденсатор, и круг повторяется опять.

В реальных схемах смешанной цепи всегда есть некоторое сопротивление, которое заставляет амплитуду направленных частиц расти меньше с каждым кругом. После нескольких смен полярности пластин, ток снижается до 0. Данный процесс называется синусоидальным затухающим волновым сигналом. Как быстро происходит этот процесс, зависит от сопротивления в цепи. Но при этом сопротивление не изменяет частоту синусоидальной волны. Если сопротивление достаточно высокой, ток не будет колебаться вообще.

Обозначение переменного тока означает, что выходя из блока питания, энергия колеблется с определенной частотой. Увеличение сопротивления способствует к снижению максимального размера текущей амплитуды, но это не приводит к изменению частоты резонанса (резонансной). Зато может образоваться вихретоковый процесс. После его возникновения в сетях возможны перебои.

Условия возникновения резонанса

Так же как и резонанс напряжений, резонанс токов возникает, когда частота источника энергии равна резонансной частоте ωр, а

Режим электрической цепи при параллельном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивной и емкостной проводимостей, называют резонансом токов.

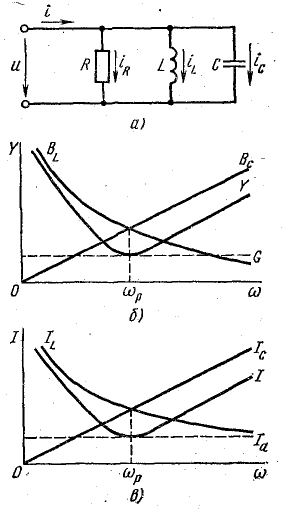
Сначала рассмотрим этот режим для схемы идеализированной цепи В этой схеме параллельно резистору R включены идеальные катушки L и конденсатор С, потери энергии в которых не учитываются.

К вопросу о резонансе токов

Реактивные проводимости зависят от частоты вынужденных колебаний. Для рассматриваемой схемы:
активная проводимость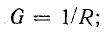

реактивные проводимости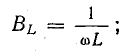


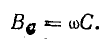
При резонансе токов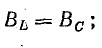



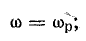
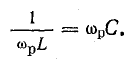
Отсюда определяют резонансную частоту: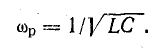

Выражение для резонансной частоты в данном случае такое же, какое было получено при рассмотрении резонанса напряжений и для частоты собственных колебаний в контуре без потерь.
Резонанс токов, так же как и резонанс напряжений, можно получить изменением параметров L и С или изменением частоты источника энергии.

Резонанс токов в цепи с переменным током

Протекание тока внутри электрической цепи с последовательным, параллельным или смешанным типом соединения элементов, вызывает получение различных режимов функционирования.

Таким образом, резонанс электрической цепи является режимом участка, который содержит элементы индуктивного и емкостного типа, а угол фазового сдвига между токовыми величинами и показателями напряжения нулевые.

В соединяемых параллельным способом конденсаторе и катушечной части наблюдается равное реактивное сопротивление, чем обусловлен резонанс.

Также должен учитываться тот факт, что для катушечной части и конденсатора характерно полное отсутствие активного сопротивления, а равенство реактивного сопротивления делает нулевыми общие токовые показатели внутри неразветвленной части электрической цепи и большие величины тока в ветвях.

В условиях параллельного соединения индуктивной катушки и конденсатора получается колебательный контур, который отличается наличием создающего колебания генератора, не подключенного в контур, что делает систему замкнутой.

Явление, сопровождающееся резким уменьшением амплитуды силы токовых величин внешней цепи, которая используется для питания параллельно включенного конденсатора и обычной индуктивной катушки в условиях приближения частоты приложенного напряжения к частоте резонанса, носит название токового или параллельного резонанса.

Расчет резонансного контура

Необходимо помнить, что явление, представленное токовым резонансом, нуждается в очень грамотном и тщательном расчете резонансного контура. Особенно важно выполнить правильный и точный расчет при наличии параллельного соединения, что позволит предотвратить развитие помех внутри системы. Чтобы расчет был правильным, требуется определиться с показателями мощности электрической сети. Среднюю стандартную мощность, которая рассеивается в условиях резонансного контура, можно выразить среднеквадратичными показателями тока и напряжения.

В условиях резонанса стандартный коэффициент мощности составляет единицу, а формула расчета имеет вид:

С целью правильного определения нулевого импеданса в условиях резонанса потребуется использовать стандартную формулу:

Резонанс колебательной частоты аппроксимируется по следующей формуле:

Резонанс колебательного контура

Чтобы получить максимально точные данныепо формулам, все получаемые в процессе расчетов значения рекомендуется не подвергать округлению. Некоторыми физиками расчеты значений резонансного контура осуществляются в соответствии с методом векторной диаграммы активных токовых величин. В таком случае грамотный расчет и правильная настройка приборов гарантирует достойную экономию при условии переменного тока.

Резонансные цепи применяются преимущественно для выделения сигнала на нужных частотах в результате фильтрования других сигналов, поэтому самостоятельные расчеты контура должны быть предельно точными.

Реактивные сопротивления индуктивности и емкости

Индуктивностью называется способность тела накапливать энергию в магнитном поле. Для нее характерно отставание тока от напряжения по фазе. Характерные индуктивные элементы — дросселя, катушки, трансформаторы, электродвигатели.

Емкостью называются элементы, которые накапливают энергию с помощью электрического поля. Для емкостных элементов характерно отставание по фазе напряжения от тока. Емкостные элементы: конденсаторы, варикапы.

Приведены их основные свойства, нюансы в пределах этой статьи во внимание не берутся.

Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине.

Принцип действия резонансных токов

Наглядное представление о резонансе токов дает колебательный контур, применяемый в электронных схемах. В его состав входит конденсатор с емкостью С и катушка с индуктивностью L, включенные параллельно. В процессе передачи энергии из электрического поля емкости в магнитное поле индуктивности возникают самозатухающие колебания с определенной частотой. Возникновение колебаний происходит благодаря активному сопротивлению R, препятствующему свободному прохождению тока.

Явление резонанса токов появляется в цепи, куда параллельно включены конденсатор и катушка. Их номиналы подобраны с таким расчетом, чтобы токи, протекающие по С и L, были равны. Поэтому в контуре С-L ток будет выше, чем его значение на остальных участках цепи.

Принцип работы такого контура заключается в следующем. При подаче питания конденсатор накапливает определенную величину заряда, равную номинальному напряжению источника тока. После этого источник отключается, а конденсатор замыкается в цепь контура, чтобы на катушку пошел разряд. Ток проходит по ней, тем самым вызывает генерацию магнитного поля. В результате создается электродвижущая сила самоиндукции, направленная навстречу току.

Максимальное значение магнитного поля достигается при полном разряде конденсатора. Таким образом, вся энергия, накопленная конденсатором, преображается в магнитное поле индуктивности. Заряженные частицы продолжают двигаться, благодаря самоиндукции катушки.

Поскольку противоток от разряженного конденсатора уже отсутствует, он подвергается повторной зарядке, но уже с изменившейся полярностью. Это приводит к преобразованию поля катушки в заряд конденсатора и повторению всего процесса. Активная составляющая R приводит к постепенному угасанию колебаний. В этом и заключается основная суть резонанса.

Понятие о резонанс токов. Условия его возникновения и способы осуществления

Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.

В1 – реактивная проводимость первой ветви,

В2 – реактивная проводимость второй ветви.

Способ возбуждения колебаний в электрическом контуре, заключающийся в генерации колебаний, за счет регулирования сигнала, управляющего возбуждением колебаний.

Резонанс токов и его признаки

Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.

Признаки резонанса токов:

Реактивные составляющие токов ветвей равны IPC = IPL и находятся в противофазе в случае, когда напряжение на входе чисто активное;

Токи ветвей превышают общий ток цепи, который имеет минимальное значение и совпадают по фазе.

Читайте также: Векторные диаграммы. Построение векторных диаграмм

Мгновенная мощь цепи синусоидального тока

Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.

Пусть мгновенные напряжение и ток определяются по формулам:

Среднее значение мгновенной мощности за период

Получим еще одну формулу:

Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P.

Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.

Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.

Преобразуем выражение (6.23):

где — мгновенная мощность в активном сопротивлении;

— мгновенная мощность в реактивном элементе (в индуктивности или в емкости).

Максимальное или амплитудное значение мощности p2 называется реактивной мощностью

Читайте также: Безопасное расстояние от ЛЭП до жилого дома: минимальные допустимые нормы

где x — реактивное сопротивление (индуктивное или емкостное).

Реактивная мощность, измеряемая в вольтамперах реактивных, расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.

Применение на практике

Рассмотрим, какая польза и вред резонанса токов и напряжений. Наибольшую пользу явления резонанса принесли в радиопередающей аппаратуре. Простыми словами, а схеме приемника установлены катушка и конденсатор, подключенные к антенне. С помощью изменения индуктивности (например, перемещая сердечник) или величины емкости (например, воздушным переменным конденсатором) вы настраиваете резонансную частоту. В результате чего напряжение на катушке повышается и приемник ловит определенную радиоволну.

Вред эти явления могут на нести в электротехнике, например, на кабельных линиях. Кабель представляет собой распределенную по длине индуктивность и емкость, если на длинную линию подать напряжение в режиме холостого хода (когда на противоположном от источника питания конце кабеля нагрузка не подключена). Поэтому есть опасность того, что произойдет пробой изоляции, во избежание этого подключается нагрузочный балласт. Также аналогичная ситуация может привести к выходу из строя электронных компонентов, измерительных приборов и другого электрооборудования – это опасные последствия возникновения этого явления.

Резонансное явление напряжения – вещь достаточно интересная и заслуживает внимания. Резонанс возможен только в индуктивных ёмкостных цепях. В линиях, где активное сопротивление велико, это явление невозможно.

Подведём итог, коротко дав ответы по данной теме:

Ответ: в индуктивных ёмкостных схемах.

Ответ: реактивные сопротивления должны быть равны.

Ответ: Поменять частоту, добавить активное сопротивление.

Надеемся, теперь вам понятно, что это за явление, условия для его появления и практическое использование.

Источник