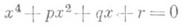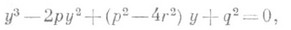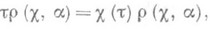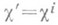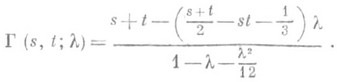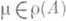что такое резольвента в мат логике

Понятие резольвенты. Метод резолюции в логике высказываний

Логические следствия.

Отношение следствия их импликаций общезначимо. Количество единиц больше в правой формуле, чем в левой.

1. Прямой путь установления _ общезначимости: F v G ≡ 1

2. Невыполняемость или обратный путь (док-во от противного): ____ _

№6. Если силлогизм условный, то одна из его посылок условная.

1.Если одна из посылок условная, а вторая посылка и вывод – категорическое высказывание, то такой силлогизм – условно-категорический. Импликация отражает ту сущность нашего мира, когда следствие может иметь несколько причин. Мир допускает переход от причины к следствию, но не обратно (П→С). Имеются 4 модуса условно-категорических силлогизмов:

Modus Ponens – утверждающий модус. Если была причина А, то будет и следствие В.

Modus Tollens – отрицающий модус.

Если не произошло В, то не было причины А.

2. Если обе посылки и вывод – условные высказывания, то такой силлогизм – условный.

3. Если одна из посылок – условное высказывание, а другая – разделительное («или – или»), то это условно-разделительный силлогизм.

Такая равносильность называется законом контрапозиции. Согласно этому закону: Высказывания A ® B и одновременно истинны либо одновременно ложны.

№9. Проверка правильности лог. выводов (доказательств) алгебраически.Для проверки правильности лог. Выводов необходимо убедится, что из конъюнкции посылок следует заключение. Для проверки правильности лог. выводов используются формулы равносильных преобразований.

Пример: предложение1: «если студент много занимается, то он успешно сдаст экзамен по мат. логике», A→B

Предложение 2: «если студент «провалился» на экзамене по математ. Логике, то он не занимался», B→A

Следует ли из первого предложение второе?

Здесь мы использовали формулы равносильных преобразований из дискретной математики.

Таким образом, следует, что это закон контрапозиции. Логический вывод подразумевает наличие посылок или гипотез и вывода или заключения.

Для проверки правильности логических выводов необходимо убедиться, что из конъюнкции посылок следует заключение.

№11. Получение следствий мз данных посылок. Получение следствий из данных посылок можно осуществить, получив СКНФ данных посылок, тогда все возможные сочетания элементарных конъюнкций и будут всевозможными следствиями из данных посылок. Нужно получить СКНФ и перебрать все возможные комбинации конъюнкций, т.е. получить булеан от членов СКНФ без одного элемента (пустого множества)

Понятие резольвенты. Метод резолюции в логике высказываний.

Если имеются два высказывания(A v B), (Ā v C), которые имеют контрарный или инверсный (A, Ā) литеры, то следствие из этих посылок является

(A v B) (Ā v C) v(B v С) =

= Ā * B v A * C v B v C ≡ 1

Такие следствия называются резольвентами (это дизъюнкция членов при контрарных литералах).

Метод основан на получение резольвент. Последовательно получаем резольвенты исходного множества формул, доказательство выполнимости которого мы ведем до тех пор, пока не получиться Æ (пустое следствие). Здесь доказательство ведется от противного. Для применения этого метода необходимо использовать КНФ.

Получили дерево доказательства. Взяты две посылки и отрицание заключения в КНФ. Следствием посылок является резольвента B, а следствием является пустое множество Æ.

№8. Условные силлогизмы. Условный силлогизм: обе посылки и вывод условные суждения.

Понятие предиката

То есть предикат – это отображение n-ой степени произвольного множества в бинарное множество В, элементы которого «истина» или «ложь».

Переменные называются предметными или пропозициональными.

Таким образом, понятие предиката является расширением понятия логическая функция.

Предикат от n переменных называется n-местным предикатом.

Вместо предметных переменных в предикат могут быть подставлены определенные значения из предметной области М, то есть константы. Также в предикат могут быть подставлены некоторые n-местные функции:

Очевидно, что высказывание – нульместный предикат, одноместный предикат – свойство, n-местный предикат – n-местное отношение.

Предикат на конечных множествах может быть задан соответствующей таблицей.

Источник

РЕЗОЛЬВЕНТА

Напр., для решения уравнения 4-й степени

(любое уравнение 4-й степени приводится к такому виду) используют кубич. Р.

Последовательное применение метода Р. позволяет свести решение любого уравнения с разрешимой группой Галуа к решению цепочки уравнений с циклич. группой Галуа. Для решения последних используются резольвенты Лагранжа.

(*)

к-рое показывает, что элементы при любом целом iинвариантны относительно G и, следовательно, являются однозначно определенными рациональными выражениями от коэффициентов многочлена f (х)и корня . Если c порождает группу характеров группы G, то имеют место равенства и для

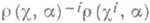
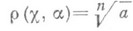
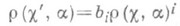
Р е з о л ь в е н т о й Г а л у а уравнения f(x)=0наз. такое неприводимое над данным полем алгебраич. уравнение у(х)=0(см. Галуа теория), что в результате присоединения одного из его корней к этому полю получается поле, содержащее все корни уравнения f(x)= 0.

Лит.:[1] В а н д е р В а р д е н Б. Л., Алгебра, пер. с нем., 2 изд., М., 1979. Л. В. Кузьмин.

2) В теории интегральных уравнений под Р. (разрешающим ядром) уравнения

(**)

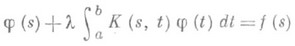
понимают функцию Г (s, t;l) переменных s, tи параметра l, при помощи к-рой решение уравнения (**) представляют в виде

если l, не есть собственное значение уравнения (**), напр. для ядра K(s, t)=s+t резольвентой является функция

1) для любых двух точек l,

2)

из R l х=0следует x=0;

Лит.:[1] И о с и д а К., Функциональный анализ, пер. с англ., М., 1967; [2] А х и е з е р Н. И., Г л а з м а н И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966; [3] К а н т о р о в и ч Л. В., А к и л о в Г. П., Функциональный анализ, 2 изд., М., 1977. В. И. Соболев.

Источник

Резольвента

Резольвента (от лат. resolvere — здесь: решать) используется в математике в различных значениях. Объединяет их все основное свойство резольвенты: решение резольвенты уравнения позволяет решить и само уравнение (или оператор).

Список значений слова или словосочетания со ссылками на соответствующие статьи. Если вы попали сюда из другой статьи Википедии, пожалуйста, вернитесь и уточните ссылку так, чтобы она указывала на статью.

Полезное

Смотреть что такое «Резольвента» в других словарях:

РЕЗОЛЬВЕНТА — 1) Р. а л г е б р а и ч е с к о г о у р а в н е н и я f(x)=0степени п алгебраическое уравнение g(y)=0с коэффициентами, рационально зависящими от коэффициентов f(x), такое, что знание корней этого уравнения позволяет найти корни данного уравнения… … Математическая энциклопедия

Резольвента — (лат. resolvens, родительный падеж resolventis развязывающий, решающий, от resolvo развязываю, решаю) (математическая), разрешающее уравнение, разрешающая функция (ядро) или разрешающие операторы. В алгебре термин «Р.»… … Большая советская энциклопедия

резольвента — резольвента, резольвенты, резольвенты, резольвент, резольвенте, резольвентам, резольвенту, резольвенты, резольвентой, резольвентою, резольвентами, резольвенте, резольвентах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов

резольвента — резольв ента, ы … Русский орфографический словарь

резольвента — и, ж., мат. Рівняння, функції чи оператор, які дають можливість простіше розв язувати якесь рівняння … Український тлумачний словник

резольвента — іменник жіночого роду … Орфографічний словник української мови

Резольвента (гомологическая алгебра) — У этого термина существуют и другие значения, см. Резольвента. Резольвента один из важных инструментов гомологической алгебры, в частности служащая для вычисления функторов править] Проективная резольвента Комплексом (X,ε) над R модулем C… … Википедия

Резольвента алгебраического уравнения — У этого термина существуют и другие значения, см. Резольвента. Резольвента алгебраического уравнения степени n это алгебраическое уравнение с коэффициентами, рационально зависящими от коэффициентов f(x), такое, что знание корней этого… … Википедия

Источник

Что такое резольвента в мат логике

В отличие от логики высказываний в логике предикатов первого порядка имеется очень большое число интерпретаций формулы, поэтому общезначимость или противоречивость этой формулы невозможно доказать проверкой ее истинности при всех возможных интерпретациях.

В логике предикатов первого порядка не существует никаких алгоритмов, проверяющих общезначимость формулы, но существуют алгоритмы, которые могут ее подтвердить.

По определению общезначимой называется формула, которая истинна при всех интерпретациях. Существуют алгоритмы нахождения такой интерпретации, при которой формула ложна. Однако, если данная формула общезначима, то не существует такой интерпретации, при которой формула была бы ложна.

Поскольку формула общезначима тогда и только тогда, когда ее отрицание противоречиво, то можно установить противоречивость отрицания данной формулы. Это служит основой для большинства современных автоматических алгоритмов поиска доказательства.

Наиболее эффективно поиск доказательств общезначимости формул осуществляется методом резолюций. Процедура поиска доказательства методом резолюций фактически является процедурой поиска опровержения, то есть вместо доказательства общезначимости формулы доказывается, что отрицание формулы противоречиво.

Дизъюнктом называется дизъюнкция литер. Множество литер можно рассматривать как синоним дизъюнкта.

Метод резолюций для логики высказываний

Метод резолюций можно применять к любому множеству дизъюнктов с целью проверки их невыполнимости (противоречивости). Рассмотрим сначала метод резолюций для логики высказываний.

A> – контрарной парой.

Метод резолюций для логики предикатов первого порядка

Нахождение в двух дизъюнктах контрарных литер выполняется довольно просто, если дизъюнкты не содержат переменных. Дизъюнкты, содержащие переменные, необходимо унифицировать, то есть найти такую подстановку, в результате которой исходные дизъюнкты будут содержать контрарные литеры.

A(f(a)) контрарны, то получим резольвенту дизъюнктов D 1 и D 2 в виде:

Дизъюнкты имеют одну или несколько резольвент, так как возможны разные подстановки. Любую подстановку можно представить с помощью множества упорядоченных пар t i /x i :

Обычно унификацию используют для того, чтобы показать, можно ли литеры привести в соответствие между собой. Для этого в литерах вместо переменных надо подставить термы.

Процесс сопоставления некоторого выражения с эталонным называется сопоставлением с образцом. Он играет важную роль в системах искусственного интеллекта.

Одна и та же задача с помощью формул логики предикатов первого порядка может быть записана в различной форме. Представляется целесообразным, особенно для выполнения формальных преобразований, использование стандартной формы записи выражений.

Источник

Вывод в логических моделях. Метод резолюций

Вывод в формальной логической системе является процедурой, которая из заданной группы выражений выводит отличное от заданных семантически правильное выражение. Эта процедура, представленная в определенной форме, и является правилом вывода. Если группа выражений, образующая посылку, является истинной, то должно гарантироваться, что применение правила вывода обеспечит получение истинного выражения в качестве заключения.

Наиболее часто используются два метода. Первый – метод правил вывода или метод естественного (натурального) вывода, названный так потому, что используемый тип рассуждений в исчислении предикатов приближается к обычному человеческому рассуждению. Второй – метод резолюций. В его основе лежит исчисление резольвент.

В этой статье рассматривается второй метод. Метод резолюций предложен в 1930г. в докторской диссертации Эрбрана для доказательства теорем в формальных системах первого порядка.

Метод резолюций опирается на исчисление резольвент. Существует теорема, утверждающая, что вопрос о доказуемости произвольной формулы в исчислении предикатов сводится к вопросу о доказуемости пустого списка в исчислении резольвент. Поэтому доказательство того, что список формул в исчислении резольвент пуст, эквивалентно доказательству ложности формулы в исчислении предикатов.

Идея метода резолюций заключается в том, что доказательство истинности или ложности выдвинутого предположения, например:

ведется методом от противного. Для этого в исходное множество предложений включают аксиомы формальной системы и отрицание доказываемой гипотезы:

Если в процессе доказательства возникает противоречие между отрицанием гипотезы и аксиомами, выражающееся в нахождении пустого списка (дизъюнкта), то выдвинутая гипотеза правильна.

Такое доказательство может быть получено на основании теоремы Эрбрана, гарантирующей, что существующее противоречие может быть всегда достигнуто за конечное число шагов, каковы бы ни были значения истинности, даваемые функциям, присутствующим в гипотезах и заключениях.

В методе резолюций множество предложений обычно рассматривается как составной предикат, содержащий несколько предикатов, соединенных логическими функциями и кванторами существования и общности. Так как одинаковые по смыслу предикаты могут иметь разный вид, то предложения преобразуются в клаузальную форму – разновидность конъюнктивной нормальной формы (КНФ), в которой удалены кванторы существования, всеобщности, символы импликации, равнозначности и др. Клаузальную форму называют сколемовской конъюнктивной формой.

В клаузальной форме вся исходная логическая формула представляется в виде множества предложений (клауз) , называемых клаузальным множеством :

Любое предложение , из которого образуется клаузальное множество , является совокупностью атомарных предикатов или их отрицаний, соединенных символом дизъюнкции:

Предикат или его отрицание называется дизъюнктом, литералом, атомом, атомарной формулой.

Сущность метода резолюций состоит в проверке, содержит или не содержит пустое предложение . Предложение является пустым, если не содержит никаких литер. Так как условием истинности является истинность всех , входящих в , то ложность какого-либо , заключающаяся в том, что множество , образующее , окажется пустым, указывает на ложность исходной логической формулы.

Если содержит пустое предложение , то противоречиво (невыполнимо). Если предложение не является пустым, то делается попытка вывода предложений пока не будет получено пустое (что всегда будет иметь место для невыполнимого ).

Для этого в двух предложениях, одно из которых состоит из одной литеры, а второе содержит произвольное число литер, находится контрарная пара литер (например и ), которая вычеркивается, а из оставшихся частей формируется новое предложение (например из и выводится ).

Предложение , вновь сформированное из имеющихся и , называется резольвентой и . Например:

Если при выводе предложений получены два однолитерных дизъюнкта, образующих контрарную пару, то их резольвентой будет пустой дизъюнкт. Так как наличие пустого дизъюнкта означает, что является ложным, то невыполнимость исходного утверждения, сформулированного в виде отрицания:

доказывает истинность выдвинутого предположения:

Поскольку в логике предикатов в предложениях допускается наличие переменных, то для нахождения контрарных пар требуется введение операции унификации (подстановки константы вместо переменной в предикаты, имеющие одинаковые предикатные символы, но разные литеры). Алгоритм унификации разработали в 1966 г. Ж. Питра и независимо от него – Дж. Робинсон: чтобы унифицировать два различных выражения, отыскивается наиболее общий унификатор – НОУ (подстановка, при которой выражение с большей описательной мощностью согласуется с выражением, имеющим малую описательную мощность). Наличие этого алгоритма позволило реализовать метод резолюций Эрбрана в виде программы для ЭВМ.

Итак, если требуется методом резолюций доказать истинность какого-либо логического утверждения, то отрицание этого утверждения преобразуется в клаузальную форму, по его предложениям выполняется поиск пустого предложения с использованием унификации и вывода резольвент. Невыполнимость отрицания подтверждает истинность рассматриваемого утверждения.

Метод резолюций получил широкое распространение из-за высокой эффективности машинной обработки. На его основе построен язык «Prolog». Однако человек в процессе рассуждений такой логикой не пользуется, и это дает основание для поиска более естественных для человеческого сознания процедур вывода заключений.

Существенным недостатком метода резолюций является то, что он предназначен только для доказательства теорем. Он не пригоден для порождения новых предложений. К тому же, если предложение не является теоремой, резолюция может привести к построению бесконечного дерева решений.

Пример: вывод решения в логической модели на основе метода резолюций.

Даны утверждения:

Требуется методом резолюций доказать утверждение «Сократ смертен».

Решение:

Шаг 1. Преобразуем высказывания в дизъюнктивную форму:

Шаг 2. Запишем отрицание целевого выражения (требуемого вывода), т.е. «Сократ бессмертен»:

Шаг 3. Cоставим конъюнкцию всех дизъюнктов (т. е. построим КНФ), включив в нее отрицание целевого выражения:

Шаг 4. В цикле проведем операцию поиска резольвент над каждой парой дизъюнктов:

Получение пустого дизъюнкта означает, что высказывание «Сократ бессмертен» ложно, значит истинно высказывание «Сократ смертен».

В целом метод резолюций интересен благодаря простоте и системности, но применим только для ограниченного числа случаев (доказательство не должно иметь большую глубину, а число потенциальных резолюций не должно быть большим). Кроме метода резолюций и правил вывода существуют другие методы получения выводов в логике предикатов.

Источник