что такое равные множества

Множества

проговаривается эта запись так: a принадлежит А, или А содержит а, или а — элемент А.

Для перечисления элементов множества используются фигурные скобки — <>. То есть, например, множество, в котором а ∈ А, b ∈ A и c ∈ A, будет записываться в таком виде:

Виды множеств.

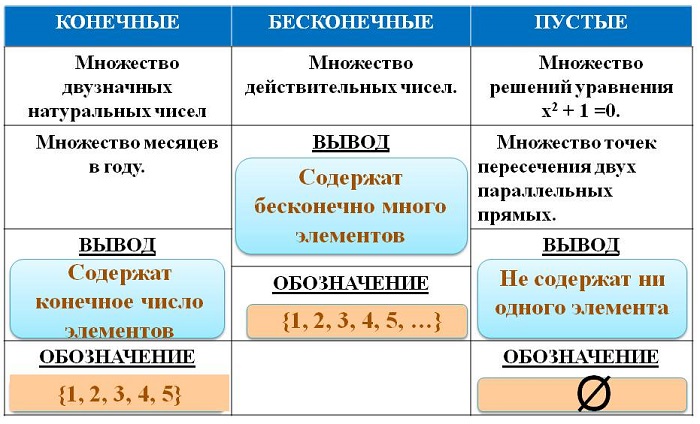
Пустые множества.

Пустое множество – это то множество, которое вообще не содержит никаких элементов. Обозначается оно цифрой 0 или специальным значком ∅.

Примером пустого множества может служить любое нелогичное понятие, противоречащее самому себе — «множество птиц, живущих на дне океана», или «множество деревьев на Луне». Поскольку оба множества лишены смысла и не отвечают реальности, то, следовательно, они являются пустыми. Скажем, количество деревьев на Луне – 0, поэтому «множество деревьев на Луне» будет пустым (не будет содержать ни одного элемента).

Равные множества.

Равные множества – это два или более множеств, состоящих из равных наборов элементов. Приведём пример. Скажем, все члены Вашей семьи находятся на кухне. Таким образом, Множество «Члены семьи на кухне» будет равно множеству «Члены семьи в квартире».

Если два множества — А и B — состоят из одинакового набора элементов, то они будут равны, то есть А = B. Элементы множеств могут перечисляться в любой последовательности, на результат это никак не влияет. Множество можно с тем же успехом записать, как , или <с, b, a>, или .

Подмножества и надмножества.

Если множества А и B состоят из одинаковых элементов , то А будет считаться подмножеством B, а B — надмножеством А. Записывается это следующим образом:

Бывает так, что множество В содержит в себе каждый из элементов множества А, но в то же время в нем присутствуют и другие элементы, множеству А не принадлежащие. В этом случае множество В становится собственным надмножеством А, в то время как множество А становится собственным подмножеством В.

Иначе говоря, если А ⊆ В, но при этом А ≠ В, то А ⊂ В, В ⊃ А.

Источник

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A₁, A₂ и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a₁, a₂ и т. д.

Границы совокупности обозначаются фигурными скобками < >.

А = <а, в, с, у>– А состоит из четырех элементов.

Записать совокупность Z согласных букв в слове «калькулятор»:

Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = , а Є N – элемент «а» принадлежит N.

Выделяют три вида множеств:

пустые (обозначаются Ø) – не имеющие элементов.

Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

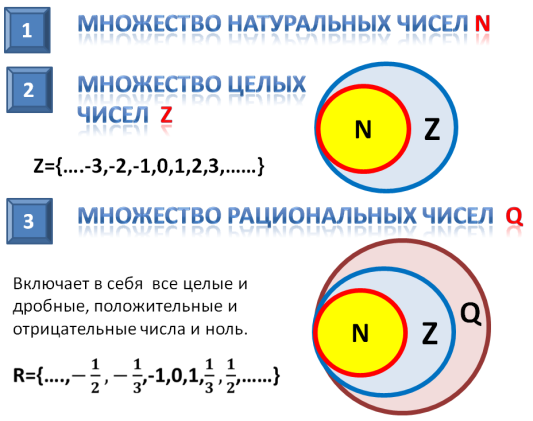
Множество натуральных чисел

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

Следовательно, N и Z являются подмножествами Q.

Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

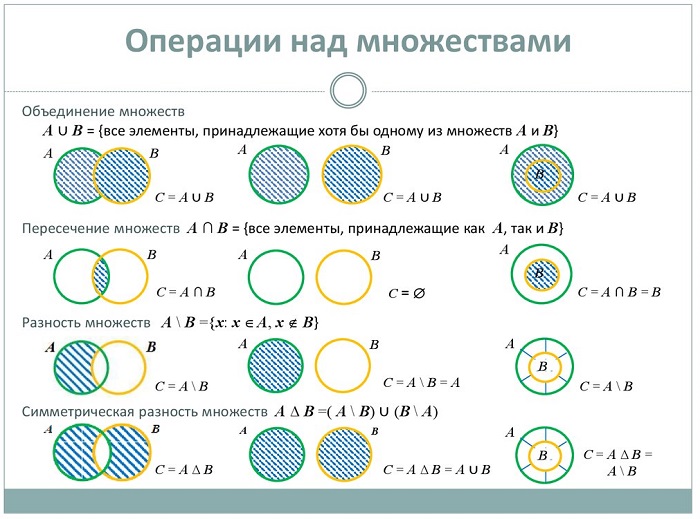
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:

Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

умножения S ∩ D = D ∩ S;

сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);

сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);

умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);

сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

если S ⊆ Fи F ⊆ J, то S ⊆ J;

если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

О других свойствах операций можно узнать из картинки:

Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Источник

Что такое множество 👨‍🎓. Свойства и операции над множествами

В этой статье рассмотрим очень важную тему, как в математике, так и в информатике – множества. Ниже Вы найдете основные определения и понятия, свойства множеств, их виды и примеры. Материал изложен таким образом, что разберется даже полный чайник. Здесь приведены, только основы, которые обычно проходятся в рамках школьной программы. Читайте!

Основные положения и обозначения

Теория множеств появилась благодаря знаменитому немецкому математику Гео́рг Ка́нтор (3 марта 1845, Санкт-Петербург — 6 января 1918, Галле (Заале)) — немецкий математик, ученик Вейерштрасса. Наиболее известен как создатель теории множеств.

Итак, начнем с основных понятий. Основное определение имеет следующий вид:

Множества (м-ва – сокр.) – наборы элементов объединенных по какому либо признаку.

Обозначаются они с помощью заглавных латинских букв, а их элементы указываются в фигурных скобках.

Примеры

​ \( S = \left\ < а, б, в, г, д, …, ю, я \right\>\) – мн-во букв русского алфавита.
\( S = \left\ < Алексей, Анатолий, Галина, …, Александр, Ирина \right\>\) – мн-во имен студентов в группе.
\( S = \left\ < 🐵, 🙈, 🙉, 🙊 \right\>\) – мн-во смайликов с изображением обезьянок.

Также стоит обговорить про принадлежность элементов к множеству. Записать её можно с помощью специального значка «принадлежности» – ​ \( \in \) ​. Так запись вида \( x \in S \) обозначает, что элемент x принадлежит множеству S.

С основным понятием разобрались, перейдем к остальной теории.

Подмножества

Подмножество – множество S1 является подмножеством S, если каждый элемент из S1 содержится (включен) в S.

Обозначают подмножества при помощи специального значка «включения», который имеет вид ​ \( \subset \) \( (\ S_1 \subset S \ ) \) ​. Также их можно отобразить схематично, используя диаграммы Эйлера, которые отображают отношения между подмножествами.

Также Вы можете выделить подмножество мужских имен, или сделать любую выборку по какому-нибудь признаку.

Мощность

Следует также выделить такое понятие, как мощность. Имеет оно следующий вид:

Мощность – количество элементов, которое содержится в множестве.

Мн-ва называются равномощными тогда и только тогда, когда количество элементов одного из них равно количеству элементов другого.

Причем неважно, какие элементы будут в этих мн-ах. Так в одном из них могут содержаться 26 букв английского алфавита, а в другом 26 марок японских автомобилей, при этом они будут равномощными.

Мощность является одним из тех свойств, благодаря которому мы можем проводить сравнение двух (или более) м-в.​​

Равенство

Необходимо сказать и про равенство. Для чайников правило будет выглядеть так:

Два (или несколько) множеств равны только тогда, когда равны все их элементы.

Теперь изучим виды и другие свойства мн-в в математике.

Существует много критериев и свойств, по которым мы можем классифицировать множества. Например, мы можем разделить их по количеству элементов:

А можем поделить их на конечные (ограниченные) и бесконечные:

Теперь рассмотрим примеры множеств в математике.

Примеры

Натуральные числа

Натуральные числа в математике – это те числа, которые мы используем при счете (1, 2, 3 и т.д.). Сюда не относятся отрицательные величины и нуль. Запись: \( N = \left\ < 1, 2, 3, 4, 5, … \right\>\).

Целые числа

Получаются из множества натуральных чисел. К ним добавляются отрицательные числа и нуль. \( Z = \left\ < 0, \pm 1, \pm 2, \pm 3, \pm 4, \pm 5, … \right\>\).

Рациональные числа

Здесь множество задается следующим образом: ​ \( Q = \left\ < \ | \ m \in Z, \ n \in N\right\> \) ​. В формуле m представляет собой целый числитель, а n – натуральный знаменатель.

Так как любое число в математике можно представить в виде дроби (например, ​ \( 5 = <5 \over 1>\) ​), то целые числа являются подмножеством рациональных чисел. Натуральные же числа являются подмножеством целых чисел.

\[ N \subset Z \subset Q \]

Эту теорию Вам надо запомнить.

Операции

В этом разделе рассмотрим основные операции (действия) над множествами в математике.

Пересечение

Чтобы поняли даже чайники, вернемся к нашим «мартышкам»:

\( S_ <1>= \left\ < 🙉, 🙊 \right\>\) — обезьянки показывающие лапки и глаза

\( S_ <2>= \left\ < 🙈, 🙉 \right\>\) — мартышки показывающие лапы и рот

Надо найти \( S_ <1>\ \cap \ S_ <2>\). Для этого воспользуемся диаграммами Эйлера — Венна:

Решение: ​ \( S_ <1>\ \cap \ S_ <2>= \left\ < 🙉 \right\>\) т.к. 🙉 ​ входит и в S1 и в S2.​

Объединение

​Решение: ​ \( S_ <1>\ \cup \ S_ <2>= \left\ < 🙈, 🙉, 🙊 \right\>\) ​

Разность

Решение: ​ \( S_ <1>\ \setminus \ S_ <2>= \left\ < 🙊 \right\>\)

Следует отметить, что здесь приведены не все операции. Например, не написано про симметрическую разность и законы Моргана. Их проходят в рамках высшей математики.

Заключение

Теперь Вы знаете, что такое мн-ва, знаете их свойства и какие операции над ними можно выполнять. Надеюсь я объяснил всю теорию так, что понял даже полный чайник. Если же у Вас возникли вопросы, то задавайте их в комментариях. Также на нашем сайте Вы можете прочитать другие статьи, например про представления чисел в компьютере. Рассказывается как выполнять с ними такие действия, как перемножение, получение суммы и деление.

Источник

Равенство множеств. Подмножество. Универсальное множество. Дополнение множества

ОСНОВНЫЕ ДАННЫЕ О РАБОТЕ

В обычной речи мы часто употребляем слово “множество”: множество людей, множество книг, множество законов, множество денег и т.д.

В математике множеством называют совокупность, набор каких-либо предметов (объектов). Это не есть точное математическое определение. Так же, как и понятия точки, числа и т.д., понятие множества является одним из тех первоначальных, наиболее общих понятий, которые приходится принимать без определения.

Примерами пустых множеств могут служить:

а) множество действительных чисел, являющихся корнями уравнения x 2 + 1 = 0;

б) множество треугольников, сумма углов которых отлична от 180°;

в) множество решений системы уравнений

.

В каком случае можно считать, что множество задано? Иногда можно задать множество, перечислив все его элементы. Например, множество учеников в классе задается перечислением фамилий в классном журнале. Это нетрудно сделать, так как такое множество содержит конечное число элементов. Однако не всякое конечное множество можно задать перечислением. Множества слонов на нашей планете или рыб в океане тоже конечные, но попробуйте их перечислить
(или пересчитать!)! Тем более нельзя перечислить все элементы бесконечного множества. Так, множество всех цифр конечное и их легко перечислить: А=<0,1,2,3,4,5,6,7,8,9>. А вот множество всех целых чисел, составленных из этих цифр, бесконечное и их уже не перечислишь. В таких случаях множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство называется характерис-тическим свойством множества. Одно и то же множество может быть задано различными характеристическими свойствами. Например, множество <2,4>может быть задано как:

а) множество четных чисел, удовлетворяющих неравенству 1

1.2. Равенство множеств. Подмножество. Универсальное множество. Дополнение множества

Приведем примеры подмножеств:

а) множество учеников 10-го класса данной школы есть подмножество множества всех учеников этой школы;

б) множество жителей Москвы является подмножеством множества жителей России;

в) множество всех квадратов есть подмножество множества всех прямоугольников;

г) множество Z всех целых чисел есть подмножество множества Q всех рациональных чисел.

Если одновременно с отношением А  В имеет место отношение В  А, то А=В. То есть, если одновременно А есть подмножество В и В есть подмножество А, то такие два множества равны.

Отношение А  В изображено с помощью диаграмм на рис. 2 а, б.

1.3. Операции над множествами: объединение, пересечение, разность

в) Обозначим через А множество целых чисел, через В множество четных чисел. Тогда А  В есть множество А, то есть А  В=А.

Примеры. а) Термин “пересечение” по существу геометрического происхождения. Пересечением прямой и плоскости, если прямая не параллельна плоскости, является их единственная общая точка. Если прямая и плоскость параллельны, то пересечение этих множеств пусто. Если же прямая лежит на плоскости, то их пересечение совпадает с множеством точек этой прямой.

Множество делителей числа 72 конечно. А множество кратных этого числа бесконечно: С=<72,144,216. 72n. >.

Бесконечно и множество кратных числа 54: D=<54,108,162,216. 54m. >.

Пересечением этих множеств является множество общих кратных для чисел 72 и 54: С  D=<216,432. >.

Наименьшее число в С  D, то есть 216, называется наименьшим общим кратным для 72 и 54.

Рис. 8 Рис. 9 Рис. 10

в) Разностью множества четных чисел и множества целых чисел является пустое множество.

1.4. Основные законы операций над множествами

Некоторые свойства объединения и пересечения множеств очень похожи на свойства хорошо известных алгебраических операций сложения и умножения. Вместе с тем многие свойства введенных операций над множествами отличаются от свойств алгебраических операций. Приведем здесь основные свойства:

Здесь роль пустого множества аналогична роли числа 0 в алгебре. Однако свойство  \А=  уже не имеет аналога в алгебре.

Первый распределительный закон аналогичен соответствую­щему распределительному закону в алгебре. А вот второй закон никакого аналога в алгебре не имеет.

Свойства, сформулированные в п.п.1-4, очевидны и не нуждаются в доказательстве. Распределительные законы в п.5 уже сложнее. Однако вместо того, чтобы их строго доказывать, лучше попытаться их понять, пользуясь диаграммами Венна.

1.5. Числовые множества. Множества точек на прямой,
задаваемые алгебраическими уравнениями и неравенствами

а) множество всех действительных чисел R;

б) множество всех рациональных чисел Q;

в) множество всех натуральных чисел N;

г) множество всех чисел вида , где n принимает все натуральные значения.

Заштрихованная часть числовой прямой содержит все точки, принад­лежащие соответст-вующему интервалу. Незакрашенные кружочки означают, что эти точки не принадлежат интервалу, а закрашенные, наоборот, означают, что эти точки принадлежат интервалу.

2. Окрестность точки. Окрестностью точки x ₀ называется любой открытый интервал, содержащий эту точку (рис. 15). Открытый интервал (a,b) служит окрестностью всякой принад-лежащей ему точки.

Пример 1. Уравнение имеет своей областью определения множество [-4,+  ). Найдем его корни. Возведем обе части уравнения в квадрат:

x + 4 = (2 – x ) 2 или x 2 – 5 x = 0.

Решим полученное квадратное уравнение:

x ( x – 5) = 0 или x ₁ = 0, x ₂ = 5.

Оба числа x ₁ = 0 и x ₂ = 5 принадлежат множеству [-4,+  ), однако число x ₂ = 5 является посторонним корнем уравнения (это показывает простая проверка: ). Таким образом множество корней данного уравнения <0> [-4,+  ). На прямой эти множества изображаются так:

.

Поэтому данное уравнение можно представить в виде совокупности двух уравнений: х = 3 и
–х = 3. Откуда получим два корня x ₁ = 3, x ₂ = –3. Геометрически эти решения можно истолковать так: расстояние от x ₁ до начала отсчета О и расстояние x ₂ до начала отсчета О равны 3 (рис. 17).

Пример 3. Неравенство | x | x |

4. Системы уравнений и неравенств с одним неизвестным.

Пример 5. Решить систему уравнений

.

или x ₁ = 3, x ₂ = –1.

При решении второго уравнения надо указать вначале его область определения: x  3. Далее, приравняв каждый из множителей нулю и решив получившиеся уравнения, будем иметь x ₁ = 3,
x ₂ = –2. Число x ₂ = –2 не принадлежит области определения [3,+  ) и является посторонним корнем. Следовательно, система уравнений имеет единственное решение: <3>.

Пример 6. Решить систему неравенств:

.

x 2 – 5 x – 6 = ( x + 1) ( x – 6).

Пересечением множеств является множество точек, на котором штриховки накладываются друг на друга.

Учитывая рассмотренные примеры 5 и 6, можно сделать один вывод. Множество решений системы уравнений или неравенств представляет собой пересечение множеств решений каждого из уравнений или неравенств, входящих в эту систему.

Иногда в процессе решения системы уравнений или неравенств получается некоторая совокупность других систем, к которым приводится данная система. В таких случаях множество решений исходной системы является объединением множеств решений каждой системы, входящей в эту совокупность. Разберем один пример.

Пример 7. Решить систему неравенств

.

Решение. Раскрывая модуль в первом неравенстве системы, получим два случая: 1) при и 2) при x – 6

1) или 2)

Найдем пересечение первого и второго множества:

Используя распределительный закон пересечения относительно объединения (см. §4), будем иметь

Множество решений исходной системы является объединением множеств (9,12] и [4,5), то есть [4,5)  (9,12].

1.6. Множества точек на плоскости, задаваемые уравнениями
и неравенствами с двумя переменными

Множества точек на плоскости можно задавать их характеристическими свойствами. В разд. 1.2 мы уже познакомились с такими примерами. Кроме такого способа задания их часто задают соотношениями между координатами точек в виде уравнений или неравенств.

Аналогично неравенство y > ax 2 + bx + c задает множество точек, лежащих по одну сторону от параболы (рис. 25 и 26), а неравенство y ax 2 + bx + c задает множество точек, лежащих по другую сторону (рис. 27 и 28).

Когда имеется система уравнений или неравенств с двумя переменными, то множество решений такой системы представляет собой пересечение множеств решений каждого уравнения или неравенства, входящего в систему.

Пример. Построить множество точек, удовлетворяющих следующим соотношениям:

б) .

Решение. В случае а) соотношения равносильны следующей системе

.

Рис. 29 Рис. 30 Рис. 31

Рис. 32 Рис. 33 Рис. 34

1.7. Отображение множеств. Взаимно-однозначное
соответствие между множествами. Понятие числовой функции

1. Рассмотрим два множества А и В. Если каждому элементу а множества А некоторым способом поставлен в соответствие один элемент b множества В, то говорят, что задано отображение множества А в множество В. Записывают это так: f:A  B или b=f(a). Через f обозначают то отображение (правило), по которому это соответствие устанавливается. С помощью диаграмм Венна это изображается так:

Если же каждый элемент множества В соответствует какому-либо элементу множества А,
то говорят, что множество А отображается на множество В (рис. 36).

В примере 1 так будет, если все стулья окажутся занятыми (то есть количество учеников и количество стульев одинаковое).

Между множествами А и В установлено взаимно-однозначное соответствие (взаимно-однозначное отображение), если каждому элементу а из А поставлен в соответствие один элемент b из B, и при этом соответствии каждый элемент b из В соответствует одному и только одному элементу а из А. С помощью диаграмм взаимно-однозначное соответствие изображено на рис. 36.

В примере 2 отображение f:A  С никогда не будет взаимно-однозначным, так как, вообще говоря, количество учеников в классе всегда меньше количества букв и, кроме того, ни одна фамилия не начинается с буквы “й” или “ь”.

Приведем теперь примеры взаимно-однозначного соответствия бесконеч­ных множеств. Одним, наиболее хорошо всем знакомым, является взаимно-однозначное соответствие между множеством всех действительных чисел R и множеством точек на прямой (числовая прямая). Разберем и другой пример. Выберем на плоскости систему координат и поставим в соответствие каждой окружности вписанный в нее квадрат, стороны которого параллельны осям координат. Мы получим взаимно-однозначное соответствие между множеством всех окружностей и множеством всех квадратов, стороны которых параллельны осям координат. Другое взаимно-однозначное соответствие между этими множествами получается, если сопоставить каждой окружности описанный вокруг нее квадрат, стороны которого параллельны осям координат.

Далее рассмотрим множество А всех точек на плоскости и множество В всех окружностей на этой плоскости, имеющие заданный радиус R. Если поставить в соответствие каждой точке а окружность радиуса R с центром в этой точке, то получим взаимно-однозначное соответствие между множествами А и В.

Функцию можно задавать разными способами. Одним из способов является табличный. Например, таблица

.

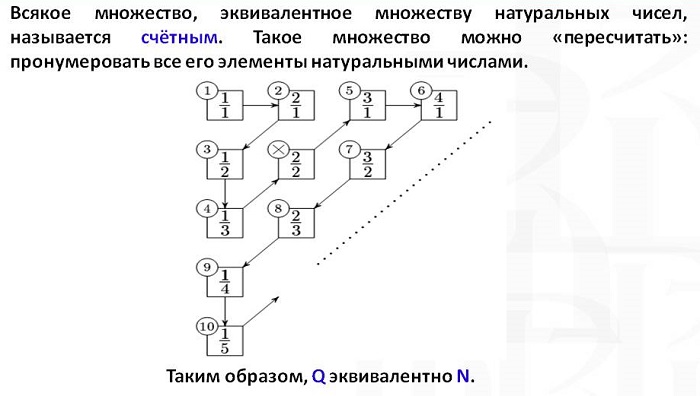
1.8. Эквивалентные множества. Счетные и несчетные множества. Мощность множества.

1. Два множества называют эквивалентными, если между ними можно установить взаимно-однозначное соответствие. Проще всего проверить эквивалентность конечных множеств. Для двух конечных множеств взаимно-однозначное соответствие можно установить лишь в случае, когда они имеют одинаковое количество элементов. Поэтому конечные множества эквивалентны тогда и только тогда, когда они имеют поровну элементов. Для бесконечных множеств не имеет смысла говорить о числе элементов. Однако и среди бесконечных множеств можно найти эквивалентные.

2. Рассмотрим множество всех натуральных чисел N=<1,2,3,4. >. Любое бесконечное подмножество А множества N эквивалентно самому множеству N. В самом деле, элементы этого подмножества можно расположить в порядке возрастания и каждому поставить в соответствие его порядковый номер (перенумеровать). Получим Так как элементов в подмножестве А бесконечно много, этот процесс можно неограниченно продолжать. Тем самым устанавливается взаимно-однозначное соответствие между А и N. Нетрудно догадаться, что множество А представляет собой числовую последовательность. Таким образом, все числовые последователь­ности, содержащие различные элементы, эквивалентны множеству натуральных чисел N.

Рассмотрим теперь множество Z всех целых чисел:

Бесконечные множества, эквивалентные множеству натуральных чисел, называются счетными множествами. Иными словами, если элементы бесконечного множества можно перенумеровать, то такое множество называется счетным. Самым простым примером счетного множества является само множество N натуральных чисел. Более сложные примеры счетных множеств мы рассмотрели выше.

Теперь сформулируем основные теоремы о счетных множествах.

Теорема 1. Каждое бесконечное подмножество А счетного множества В счетно.

Теорема 2. Объединение конечного или счетного множества счетных множеств счетно.

Доказывать эти теоремы мы не будем, хотя отметим, что доказательство теоремы 1 почти ничем не отличается от приведенного выше рассуждения, когда доказывалась эквивалентность между множеством N и его подмножест­вом А.

3. До сих пор мы рассматривали лишь такие бесконечные множества, которые являются счетными. Однако не все бесконечные множества счетные, существуют и такие, элементы которых нельзя перенумеровать. Простейшим примером такого множества является множество всех точек конечного интервала, например, интервала (0,1). Ясно, что в этом множестве содержится счетное подмножество. В качестве такого подмножества можно указать, например, числовую последовательность . Но оказывается, что точек в интервале (0,1) “намного” больше, чем точек этой последователь­ности. Точнее говоря, множество точек интервала (0,1) несчетно, то есть нельзя установить взаимно-однозначного соответствия между множеством точек интервала (0,1) и множеством натуральных чисел N. Доказательство этого утверждения мы проводить не будем. Легко сообразить, что любой другой интервал длины 1 на числовой прямой эквивалентен интервалу (0,1). Вообще, произвольный интервал (a,b) конечной длины эквивалентен интервалу (0,1). Взаимно-однозначное соответствие между ними можно установить так, как показано на рис. 38.

Точно так же любой отрезок (замкнутый интервал) эквивалентен отрезку [0,1] (рис. 39).

Это утверждение означает, что квадрат содержит “столько же” точек, что и отрезок, хотя на первый взгляд кажется, что в нем должно быть “гораздо больше” точек. Доказательство этой теоремы мы приводить не будем. Кстати сказать, множества точек плоскости и пространства тоже имеют мощность континуума.

Источник