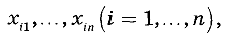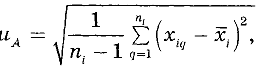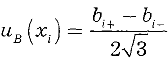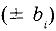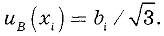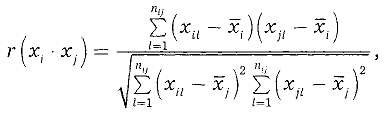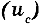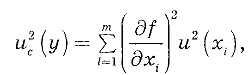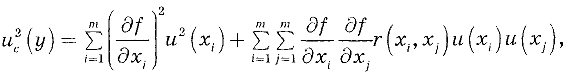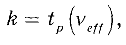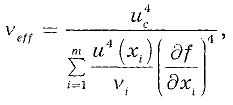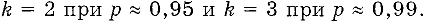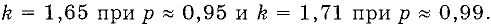что такое расширенная неопределенность результатов измерений

расширенная неопределенность

3.8 расширенная неопределенность: Величина, определяющая ожидаемый интервал вокруг результата измерения, который может охватить большую часть распределения возможных фактических значений измерения.

3.5 расширенная неопределенность (expanded uncertainty): Величина, характеризующая интервал вокруг результата измерения, в котором, можно ожидать, находится большая часть значений распределения, которые с достаточным основанием могут быть приписаны измеряемой величине.

3.7 расширенная неопределенность (expanded uncertainty): Величина, характеризующая интервал вокруг результата измерения, в котором, можно ожидать, находится большая часть значений распределения, которые с достаточным основанием могут быть приписаны измеряемой величине.

1 Часть может быть рассмотрена как вероятность охвата или уровень доверительной вероятности для интервала.

2 Для того чтобы связать конкретный уровень доверительной вероятности с интервалом, определяющимся расширенной неопределенностью, требуется сделать точные или неточные предположения относительно распределения вероятностей, характеризующего результат измерения и связанную с ним суммарную стандартную неопределенность. Уровень доверительной вероятности, который может быть приписан интервалу, может быть известен только с той степенью достоверности, с которой делаются подобные предположения.

3 Расширенную неопределенность называют полной неопределенностью в Руководстве по выражению неопределенности измерения ЕН 13005.

3.8 расширенная неопределенность (expanded uncertainty): Величина, характеризующая интервал вокруг результата измерений, в котором, можно ожидать, находится большая часть значений распределения, которые с достаточным основанием могут быть приписаны измеряемой величине.

1 Часть может быть рассмотрена как вероятность охвата или уровень доверительной вероятности для интервала.

2 Для того, чтобы связать конкретный уровень доверительной вероятности с интервалом, определяющимся расширенной неопределенностью, требуется сделать точные или неточные предположения относительно распределения вероятностей, характеризующегося результатом измерения и связанной с ним суммарной стандартной неопределенностью. Уровень доверительной вероятности, который может быть приписан интервалу, может быть известен только с той степенью достоверности, с которой делаются подобные предположения.

3 Расширенную неопределенность называют полной неопределенностью в Руководстве по выражению неопределенности измерения ЕН 13005.

расширенная неопределенность (expanded uncertainty): Величина, определяющая ожидаемый интервал вокруг результата измерения, для охвата большей части распределения значений, которые могут быть обосновано приписаны к измеряемой величине.

[Руководство по выражению неопределенности [2]]

3.40 расширенная неопределенность [uncertainty (expanded)]: Величина, определяющая интервал вокруг результата измерений, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли бы быть приписаны измеряемой величине.

3.12 расширенная неопределенность : Величина, определяющая интервал вокруг результата измерения, в пределах которого, можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли быть приписаны измеряемой величине.

[ title=’Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений» ‘ [2], подраздел 3.1]

3.12 расширенная неопределенность: Величина, определяемая интервалом вокруг математического ожидания результатов измерений, охватывающим большую долю распределения значений, которые обоснованно могут быть приписаны измеряемой величине.

3.5.6 расширенная неопределенность: Величина, определяющая интервал вокруг результата измерения, в пределах которого, можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могут быть приписаны измеряемой величине.

3.5.5 расширенная неопределенность (expanded uncertainty): Величина, характеризующая интервал вокруг результата измерения, в котором, можно ожидать, находится большая часть значений распределения, которые с достаточным основанием могут быть приписаны измеряемой величине.

[ISO Guide 98:1995, 2.3.5]

Смотри также родственные термины:

3.4.3 расширенная неопределенность (для методики или средства измерений) (overall uncertainty ): Величина, характеризующая полную неопределенность результата, полученного с помощью средства измерений или методики.

3.4.2 расширенная неопределенность (методическая или инструментальная) U, % (overall uncertainty (of a measuring procedure or of an instrument)): Количественная характеристика неопределенности результата измерения, обусловленной инструментальной и методической погрешностью, выраженная как комбинация смещения и прецизионности, обычно вычисляемая по формуле

3.10 расширенная неопределенность U : Величина, определяющая интервал вокруг результата измерений, в пределах которого находится большая часть значений, с достаточным основанием могущих быть приписанными измеряемой величине.

3.1.7 расширенная неопределенность U: Величина, определяющая интервал вокруг результата измерений, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли бы быть приписаны измеряемой величине.

3.1.19 расширенная неопределенность аттестованного значения стандартного образца :Неопределенность аттестованного значения СО, представляющая собой величину, определяющую интервал вокруг аттестованного значения СО, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могут быть приписаны аттестуемой характеристике СО.

Полезное

Смотреть что такое «расширенная неопределенность» в других словарях:

Расширенная неопределенность — (expanded uncertainty): величина, определяемая интервалом вокруг математического ожидания результатов измерений, охватывающих большую долю распределения значений, которые обоснованно могут быть приписаны измеряемой величине. Источник:… … Официальная терминология

расширенная неопределенность U — 3.10 расширенная неопределенность U : Величина, определяющая интервал вокруг результата измерений, в пределах которого находится большая часть значений, с достаточным основанием могущих быть приписанными измеряемой величине. Примечание… … Словарь-справочник терминов нормативно-технической документации

расширенная неопределенность; U — 3.10 расширенная неопределенность; U: Неопределенность, представляющая собой интервал вокруг результата измерений, в пределах которого находится большая часть значений, с достаточным основанием могущих быть приписанными измеряемой величине.… … Словарь-справочник терминов нормативно-технической документации

расширенная неопределенность — išplėstinė neapibrėžtis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, apibrėžiantis matavimo rezultato sritį, kurioje tikimasi didžiausios verčių, kurias pagrįstai galima būtų priskirti matuojamajam dydžiui, pasiskirstymo… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

расширенная неопределенность (для методики или средства измерений) — 3.4.3 расширенная неопределенность (для методики или средства измерений) (overall uncertainty ): Величина, характеризующая полную неопределенность результата, полученного с помощью средства… … Словарь-справочник терминов нормативно-технической документации

расширенная неопределенность аттестованного значения стандартного образца — 3.1.19 расширенная неопределенность аттестованного значения стандартного образца :Неопределенность аттестованного значения СО, представляющая собой величину, определяющую интервал вокруг аттестованного значения СО, в пределах которого, как можно… … Словарь-справочник терминов нормативно-технической документации

расширенная неопределенность (методическая или инструментальная) U, — 3.4.2 расширенная неопределенность (методическая или инструментальная) U, % (overall uncertainty (of a measuring procedure or of an instrument)): Количественная характеристика неопределенности результата измерения, обусловленной инструментальной… … Словарь-справочник терминов нормативно-технической документации

относительная расширенная неопределенность — 3.13 относительная расширенная неопределенность : Отношение расширенной неопределенности к значению оценки измеряемой величины, выраженное в процентах. [ГОСТ 8.586.1, подраздел 3.5] Источник … Словарь-справочник терминов нормативно-технической документации

неопределенность — 3.8 неопределенность K: Величина, определяющая меру неточности измерения (оценки) параметра вибрационной характеристики u. Примечание Определение неопределенности измерений (оценки) при заявлении вибрационной характеристики изделия по приложению… … Словарь-справочник терминов нормативно-технической документации

неопределенность измерений — 3.7 неопределенность измерений : Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые могли бы быть обоснованно приписаны измеряемой величине. Примечания 1 Термины по 3.7 3.10 соответствуют title=… … Словарь-справочник терминов нормативно-технической документации

Источник

Аккредитация в Росаккредитации

форум для аккредитованных лабораторий

Вопросы учета неопределенности измерений

#1 Вопросы учета неопределенности измерений

Как видим, оба основополагающих документа дают примерно одинаковые определения, которые коротко можно объединить простой фразой: неопределенность есть мера рассеяния результатов измерения.

Пожалуй, для большинства читателей этих знаний достаточно, и им можно сразу перейти к следующим разделам, посвященным оценке неопределенности. Тем же, кто желает чуть глубже понять природу неопределенности, разобраться, чем неопределенность отличается от привычного со школьной скамьи термина «погрешность», будет полезно то, что сказано далее (а тому, кто хочет погрузиться совсем глубоко, мы советуем изучить Приложение D ГОСТ 34100.3 (действует с 01.09.2018 взамен ГОСТ Р 54500-3).

Для начала отметим, что введение в метрологию термина «неопределенность» привело не столько к появлению каких-то новых аналитических выражений и вычислений, сколько к изменению общего взгляда на то, что такое измерение.
Сравним два определения:

Таким образом, если ещё совсем недавно процесс измерения воспринимался исключительно как сравнение с единицей величины, то есть с эталоном, то теперь — это совокупность любых операций, которые приводят к какому-то значению.

Заметим, что такая трансформация понятий естественна: старые метрологические концепции выросли из эпохи палат мер и весов, а сегодня для многих измерений вообще не существует эталонов — например, в информационных технологиях, в медицинских и биологических исследованиях, при измерении интенсивности транспортных потоков и пр.

Следствием этих фундаментальных изменений стал постепенный отказ от применения термина «погрешность»:

Погрешность измерений: разность между измеренным значением величины и опорным значением величины ( опорное значение = значение величины, которое используют в качестве основы для сопоставления со значениями величин того же рода; опорное значение величины может быть истинным значением величины, подлежащей измерению, в этом случае оно неизвестно, или принятым значением величины, в этом случае оно известно [РМГ-29-2013]).

Опорное значение величины заранее известно на эталоне, когда, например, калибруется какое-то средство измерения. Но при натурных измерениях опорное значение неизвестно, поэтому и говорить о погрешности в этих случаях весьма проблематично.

Более того, как хорошо объяснено в ГОСТ 34100.3 (Приложение D), при натурных измерениях мы почти никогда не измеряем то, что хотим измерить: мы имеем дело с реализованной величиной. Простейший пример — измерение шума оборудования при наличии помех. Мы измеряем суммарные уровни звука и приписываем их испытуемой машине. Конечно, мы стараемся исключить или учесть помехи, однако не можем сделать это с абсолютной точностью.

Таким образом, возникает ещё одна составляющая неуверенности в результате (неопределенности), связанная с учетом различий между реализованной величиной и величиной, подлежащей измерению.

В отличие от погрешности натурных измерений, составляющие неопределенности (отклонения реализованной величины от измеряемой, погрешности средств измерений и пр.) могут быть оценены. Это позволяет нам прогнозировать результаты последующих замеров: с некоторой вероятностью мы можем ожидать, что они окажутся в пределах области значений, размеры которой характеризуются рассчитанной нами неопределенностью. Для многих практических применений этого вполне достаточно, так как позволяет сопоставлять результаты измерений различных лабораторий и использовать их в технических расчетах.

В руководствах по оценке неопределенности (ISO/IEC 98-3:2003) соотношение понятий «значение величины», «погрешность», «неопределенность» рассмотрено, можно сказать, на философском уровне осмысления, который нам представляется избыточным для большинства практиков. На наш взгляд, сказанного выше вполне достаточно для понимания сути вопроса.

В каких же случаях следует пользоваться понятиями «неопределенность» и «погрешность». Ответ на этот вопрос находим в РМГ-91-2009 (далее приведены выдержки из этого документа):

В аттестованных методиках измерений (МВИ) устанавливают совокупность операций и правил, выполнение которых обеспечивает получение результата измерения с погрешностью, не превышающей допускаемых пределов (норм погрешности измерений). В таких МВИ рекомендуется использовать понятие «погрешность» в виде нормативных пределов погрешностей. Результаты измерения по этим МВИ не требуется сопровождать конкретной характеристикой точности.

Примечание авторов статьи: примеры таких МВИ — методики прямых измерений.

Результаты измерения по МВИ, характеристики точности которых определяют в процессе или после их применения, рекомендуется сопровождать оценками неопределенности измерения. Оснований для оперирования погрешностью в таких случаях нет.

Нормирование метрологических характеристик средств измерений осуществляют, оперируя понятием «погрешность» и руководствуясь ГОСТ 8.401 и ГОСТ 8.009. При этом характеристики погрешности используют как пределы допускаемых погрешностей средств измерений данного типа.

До недавнего времени гигиеническая оценка физических факторов осуществлялась без учета неопределенности, хотя требования приводить её в протоколах измерения действуют уже не один год. В 2017 году вступили в силу новые санитарные нормы и правила СанПиН 2.2.4.3359-16, в пункте 1.5 которых сказано: «Оценка фактических уровней производственных физических факторов должна проводиться с учетом неопределенности измерений». Каким же образом это делать? В настоящее время существует несколько подходов к учету неопределенности при подтверждении соответствия требованиям.

а) Подход ГОСТ ИСО 10576-1: если интервал неопределенности результатов измерений находится внутри области допустимых значений, принимают решение о соответствии; если интервал неопределенности результатов измерений находится внутри области недопустимых значений, то принимают решение о несоответствии; если. не может быть принято решение ни о соответствии, ни о несоответствии требованиям, результат оценки является неокончательным. Этот подход вполне обоснован, если мы хотим проверить, соответствует ли какая-то техническая характеристика нормативному значению с учетом пределов допуска. Однако его применение для сопоставления измеренного значения с гигиеническим нормативом, устанавливающим пределы безопасности среды обитания, вызывает сомнения. Ни один из опрошенных нами гигиенистов не осмелился однозначно ответить на вопрос: является ли, с точки зрения безопасности здоровья, приемлемой ситуация, когда с 50%-й вероятностью измеряемый фактор находится в зоне недопустимых значений? И если нет, то почему мы должны считать такой случай не окончательным решением?

б) Подход ГОСТ 23337-2014: решение о соответствии принимается только в том случае, если соответствующая (чаще всего верхняя) граница одностороннего интервала неопределенности не превышает нормативного значения. Этот подход можно переформулировать простой, хотя и не очень точной фразой: «неопределенность надо прибавлять к результату», то есть учитывать в худшую сторону.

Примерно такой же подход ещё недавно действовал в технической акустике: в 1996 году ТК29 МЭК была одобрена политика учета неопределенности, ключевым критерием которой был следующий: «измеренные отклонения от нормативных значений, увеличенные на расширенную неопределенность измерений, не должны выходить за пределы допуска». То есть и в этом случае с нормативом (пределом допуска) сравнивалось измеренное значение (отклонение), увеличенное на расширенную неопределенность.

в) Подход ГОСТ 12.1.003 (последняя редакция): с нормативом сравнивается непосредственно результат измерения (без прибавления/вычитания неопределенности), при этом неопределенность не должна выходить за оговоренные рамки. Такой подход достаточно популярен сегодня в технике, например, он реализован в уточненной политике уже упомянутого выше ТК29 МЭК. Однако применить его в практике гигиенического регулирования всех физических факторов неионизирующей природы в данный момент очень сложно из-за того, что непонятны принципы назначения максимально допустимых значений неопределенности для всех нормируемых показателей. Возможно, через какое-то время практика использования неопределенности в санитарно-эпидемиологической сфере позволит установить такие нормативные значения.

Учет неопределённости при оценке результатов измерений физических факторов.

Источник

Неопределенность измерений в метрологии

Определения погрешности и неопределенности измерений.

История возникновения термина «неопределенность измерений».

Термины используемые при расчете неопределенности.

Соотношение терминов теории неопределенности с терминами классической теории точности (в скобках):

Подробно о типах определённости и их расчётах рассказано в статье «Понятие и типы неопределенностей. ГОСТ 34100.3-2017»

Оценка результата измерений в терминах «погрешность измерений».

Рис.1. Диапазон возможных значений при погрешности

Оценка результата измерений в терминах «неопределенность измерений».

Рис.2. Диапазон возможных значений при неопределенности

Рис.3. Интервал значений при расчете неопределенности

Расчёт неопределённости с применением приборов.

В следующей статье «Расчет неопределенности результатов измерений | пример для люксметра «еЛайт»» мы рассмотрим практический пример как вручную вычислить неопределенность измерений освещенности, используя люксметр-пульсметр-яркомер еЛайт02. В некоторых современных приборах такой расчёт неопределённости уже осуществляется автоматически, как, например, в самом доступном люксметре с поверкой еЛайт-мини.

Рис.4. Профессиональный измеритель освещённости еЛайт01 с функцией автоматического расчёта неопределённости измерений.

Рис.5. Термоанемометр-гигрометр-барометр ЭкоТерма Максима 01 с функцией автоматического расчёта неопределённости измерений.

Выводы.

Отличие понятия «погрешности» от «неопределенности»:

Понравился материал? Поделитесь им в соцсетях:

Источник

Неопределенность измерений в метрологии

Неопределенность измерений и ее отражение в описании результатов

Понятие «неопределенность», как наименование количественно оцениваемого свойства измерения, является относительно новым в метрологии. Термин «неопределенность» введен «Руководством по предоставлению неопределенности измерений» (далее «Руководство»), поскольку «погрешность» — идеализированное понятие, и не может быть известна точно.

Неопределенность (измерения) — это параметр, связанный с результатом измерения, характеризующий дисперсию значений, которые могли быть обоснованно приписаны измеряемой величине.

Руководство устанавливает общие правила оценивания и выражения неопределенности измерения, которые следует соблюдать при любых уровнях точности в широком спектре измерений, включая:

К оцениванию неопределенности следует приступать только после исключения результатов с грубыми погрешностями и исправления результатов измерений (исключения систематических составляющих погрешностей). Такой подход позволяет обоснованно применять математический аппарат теории вероятностей и математической статистики к «исправленным результатам измерений.

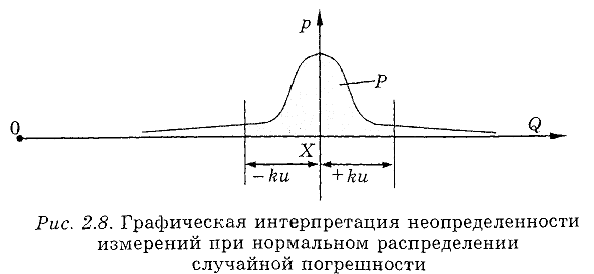
Неопределенность измерения в некоторых информационных источниках трактуется как мера возможной погрешности оцененного значения измеряемой величины, либо как оценка, характеризующая диапазон значений, в пределах которого находится истинное значение измеряемой величины. Под неопределенностью измерений фактически подразумевают то, что результат измерений фиксируется интервалом значений, а не конкретной точкой на числовой оси физической величины, при этом координата истинного значения остается неизвестной (неопределенной). В более широком смысле можно говорить также и о неопределенности «закона распределения» результатов многократных наблюдений при измерении конкретной физической величины. Графическое отображение неопределенности представлено на рис. 2.8.

На рисунке отражены качественная оценка неопределенности (нормальное распределение), а также ее количественные оценки (расширенная неопределенность 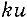при выбранной доверительной вероятности ).

В руководстве используются следующие термины и определения:

Стандартная неопределенность — неопределенность результата измерения, выраженная как стандартное отклонение.

Оценка (неопределенности) по типу А — метод оценивания неопределенности путем статистического анализа рядов наблюдений.

Оценка (неопределенности) по типу В — метод оценивания неопределенности иным способом, чем статистический анализ рядов наблюдений.

Суммарная стандартная неопределенность — стандартная неопределенность результата измерения, когда результат получают из значений ряда других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других величин, взвешенными в соответствии с тем, как результат измерения изменяется в зависимости от изменения этих величин.

Расширенная неопределенность — величина, определяющая интервал вокруг результата измерения, в пределах которого можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли быть приписаны измеряемой величине.

Коэффициент охвата — числовой коэффициент, используемый как множитель суммарной стандартной неопределенности для получения расширенной неопределенности. При нормальном распределении обычно применяют значения коэффициента охвата 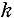, называемого также «коэффициент покрытия» в диапазоне от 2 до 3.

Установление связи между выбранным уровнем доверия и интервалом, характеризующим расширенную неопределенность, требует явных и неявных предположений относительно закона распределения вероятностей.

Классификация методов оценивания неопределенности на тип А и тип В представляет два различных способа получения оценки составляющих неопределенности. Оба типа основаны на вероятностном оценивании распределений случайных величин, а составляющие неопределенности при любом типе оценивания количественно представляют как оценки дисперсией или стандартных отклонений. Различия двух типов оценивания заключаются в методе получении оценки: прямое получение оценки путем статистического анализа рядов наблюдений (оценивание неопределенности по типу А) или получение оценки без непосредственного статистического анализа рядов наблюдений (оценивание неопределенности по типу В). Стандартную неопределенность при оценивании по типу В получают из предполагаемой функции плотности вероятностей, причем используют готовые оценки, полученные в ходе разнообразных метрологических мероприятий.

Наиболее распространенным способом формализации неполного знания о распределении величины является постулирование равновероятного распределения возможных значений этой величины в указанных границах.

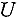
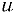
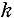
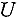
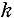
Расширенную неопределенность получают умножением суммарной стандартной неопределенности , на коэффициент охвата . Фактически представляет собой доверительный интервал, который с выбранной вероятностью накрывает истинное значение измеряемой величины. Коэффициент охвата зависит от вида приписанного распределения и выбранной доверительной вероятности.

По определению суммарная стандартная неопределенность измерения, представляет собой оценку среднего квадратического отклонения результата косвенных измерений, поскольку результат измерения получают из значений ряда других величин. Суммарную стандартную неопределенность при этом рассчитывают как значение квадратного корня из суммы дисперсий (или ковариаций) этих величин с учетом весовых коэффициентов.

Фактически понятие «суммарная стандартная неопределенность» следует рассматривать в двух вариантах:

Значения составляющих, входящих в суммарную неопределенность, могут быть получены путем оценивания как по типу А, так и по типу В, главное требование — под корнем эти составляющие должны быть представлены оценками соответствующих дисперсий.

Вычисление стандартной неопределенности по типу А

Исходными данными для вычисления являются результаты многократных измерений:

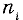
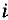
где — число измерений -й входной величины.

Стандартную неопределенность единичного измерения 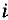-й входной величины вычисляют по формуле:

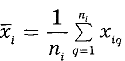
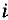
где — среднее арифметическое результатов измерений -й входной величины.

Стандартную неопределенность измерений 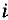-й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле:

Вычисление стандартной неопределенности 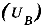по типу В

Исходными данными для вычисления является следующая информация:

-данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;

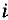
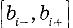
Неопределенности этих данных обычно представляют в виде границ отклонения значений величины от ее точечной оценки. При неполном знании о неопределенности некоторой -й входной величины обычно постулируют равновероятное распределение возможных значений этой величины в указанных (нижней и верхней) границах . При этом стандартную неопределенность, вычисляемую по типу В, определяют по формуле:

а для симметричных границ

В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.

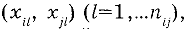
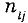
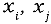
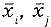
Для вычисления коэффициента корреляции используют согласованные пары результатов измерений где — число согласованных результатов измерений:

где — результаты прямых измерений, — средние значения результатов прямых измерений.

Вычисление суммарной стандартной неопределенности

В случае некоррелированных результатов измерений 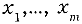оценку дисперсии суммарной стандартной неопределенности вычисляют по формуле:

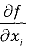
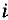
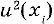
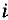
где — весовой коэффициент -ой стандартной неопределенности, — -ая стандартная неопределенность.

В случае коррелированных результатов измерений 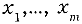оценку дисперсии суммарной стандартной неопределенности вычисляют по формуле:

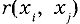
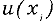
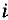
где — коэффициент корреляции; — стандартная неопределенность входной величины , вычисленная по типу А или по типу В.

Выбор коэффициента охвата 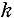при вычислении расширенной неопределенности

В общем случае коэффициент охвата выбирают в соответствии с формулой:

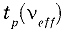
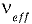
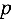
где — квантиль распределения Стьюдента с эффективным числом степеней свободы и доверительной вероятностью (уровнем доверия) .

Число степеней свободы определяют по формуле:

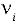
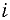
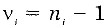
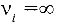
где — число степеней свободы при определении оценки -й входной величины: — для вычисления неопределенностей по типу A; — для вычисления неопределенностей по типу В.

Во многих практических случаях при вычислении неопределенностей измерений делают предположение о нормальном законе распределения возможных значений измеряемой величины и полагают:

При допущении распределения данных по закону равной вероятности полагают:

При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации для возможности проанализировать или повторить весь процесс получения результата измерений и вычисления неопределенностей измерений, а именно:

Эта лекция взята со страницы лекций по нормированию точности:

Возможно эти страницы вам помогут:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник