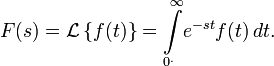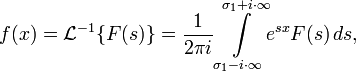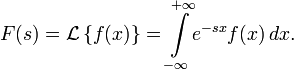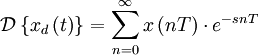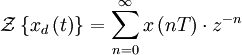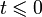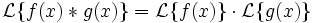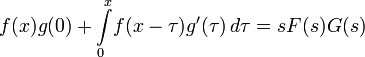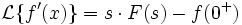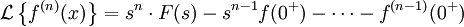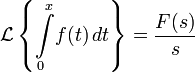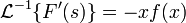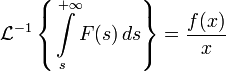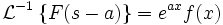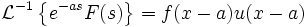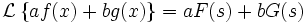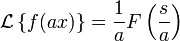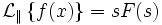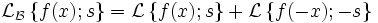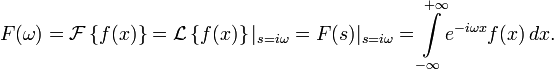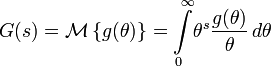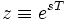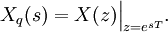что такое преобразование лапласа
Лапласа преобразование
Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию 

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Содержание
Определение
Прямое преобразование Лапласа
Преобразованием Лапласа функции действительной переменной 

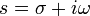
Правая часть этого выражения называется интегралом Лапласа.
Обратное преобразование Лапласа
Обратным преобразованием Лапласа функции комплексного переменного 

где 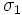
Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции 
Двусторонее преобразование Лапласа определяется следующим образом:
Дискретное преобразование Лапласа
Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.
Различают 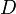
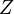
Пусть 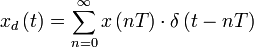
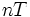
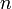
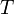
Тогда применяя преобразование Лапласа получим:
Если применить следующую замену переменных: 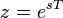
получим Z-преобразование:
Свойства и теоремы
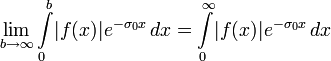
Преобразование Лапласа 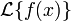
Примечание: это достаточные условия существования.
Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:
1. Если изображение F(s) — аналитичная функция для 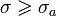
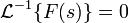
2. Пусть 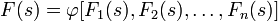
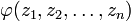
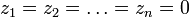
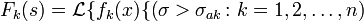
Примечание: это достаточные условия существования.
Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов.
Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.
Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа.
Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент.
Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком.
Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, деленный на свой аргумент.
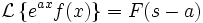
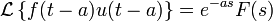
Теоремы о начальном и конечном значении (предельные теоремы):
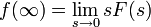
Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, к примеру, используется для анализа устойчивости траектории динамической системы.
Умножение на число
Прямое и обратное преобразование Лапласа некоторых функций
Ниже представлена таблица преобразования Лапласа для некоторых функций.
Применения преобразования Лапласа
Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники.
Связь с другими преобразованиями
Фундаментальные связи
Практически все интегральные преобразования имеют схожую природу и могут получаться одно из другого через выражения соответствия. Многие из них являются частными случаями других преобразований. Далее даны формулы, связывающие преобразования Лапласа с некоторыми другими функциональными преобразованиями.
Преобразование Лапласа-Карсона
Преобразование Лапласа-Карсона получается из преобразования Лапласа путём домножения его на комплексную переменную.
Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа 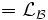
Преобразование Фурье
Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом s = iω :
Примечание: в этих выражениях опущен масштабирующий множитель 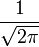
Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.
Преобразование Меллина
Преобразование Меллина и обратное преобразование Меллина связаны с двусторонним преобразованием Лапласа простой заменой переменных. Если в преобразовании Меллина
Z-преобразование
Z-преобразование — это преобразование Лапласа решётчатой функции, производимое с помощью замены переменных:
где 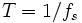
Преобразование Бореля
Интегральная форма преобразования Бореля идентична преобразованию Лапласа, существует также обобщённое преобразование Бореля, с помощью которого использование преобразования Лапласа распространяется на более широкий класс функций.
Библиография
См. также
Внешние ссылки
Преобразование Абеля | Преобразования Бесселя | Преобразование Бушмана | Преобразование Гильберта | Преобразование Конторовича — Лебедева | Преобразование Лапласа | Преобразование Мейера | Преобразование Мелера — Фока | Преобразование Меллина | Преобразование Нерейна | Преобразование Радона | Преобразование Стильтьеса | Преобразование Фурье | Преобразование Хартли | Преобразование Хенкеля
Полезное
Смотреть что такое «Лапласа преобразование» в других словарях:
Лапласа преобразование — преобразование, переводящее функцию f (t) действительного переменного t (0 Большая советская энциклопедия
ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — трансформация Лапласа, в широком смысле интеграл Лапласа вида где интегрирование производится по нек рому контуру Lв плоскости комплексного переменного z, ставящий в соответствие функции f(z). определенной на L, аналитич. функцию… … Математическая энциклопедия
ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — в геометрии переход от одной фокальной сети конгруэнции к другой фокальной сети той же конгруэнции. Понятие Л. п. сети ввел Г. Дарбу (G. Darboux, 1888), обнаруживший, что аналитич. реобразование решений уравнения Лапласа где а, b, с известные… … Математическая энциклопедия
Преобразование Фурье — Преобразование Фурье операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие … … Википедия
Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917 го года[1]. Важнейшее свойство преобразования Радона обратимость, то есть возможность… … Википедия
Преобразование Гегенбауэра — Преобразование Гегенбауэра интегральное преобразование функции : где многочлены Гегенбауэра. Если функция разлагается в обобщенный ряд Фурье по многочленам Гегенбауэра, то им … Википедия
Преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются… … Википедия
Преобразование — одно из основных понятий математики, возникающее при изучении соответствий между классами геометрических объектов, классами функций и т.п. Например, при геометрических исследованиях часто приходится изменять все размеры фигур в одном и… … Большая советская энциклопедия
Преобразование Хенкеля — В математике, преобразование Ханкеля порядка ν функции f(r) задаётся формулой: где Jν функция Бесселя первого рода порядка ν и ν ≥ −1/2. Обратным преобразованием Ханкеля функции Fν(k) называют следующее выражение: которое можно проверить с… … Википедия
Преобразование Лапласа
Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию 

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Содержание
Определение
Прямое преобразование Лапласа
Правая часть этого выражения называется интегралом Лапласа.
Обратное преобразование Лапласа
Обратным преобразованием Лапласа функции комплексного переменного 

где 
Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции 

Двустороннее преобразование Лапласа определяется следующим образом:
Дискретное преобразование Лапласа
Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.
Различают 

Пусть 



Тогда применяя преобразование Лапласа получим:
Если применить следующую замену переменных:
получим 
Свойства и теоремы
Если интеграл Лапласа абсолютно сходится при 
то он сходится абсолютно и равномерно для 







Преобразование Лапласа 
Примечание: это достаточные условия существования.
Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:
Примечание: это достаточные условия существования.
Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов:
Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.
Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа:
В более общем случае (производная 
Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала, делённое на свой аргумент:
Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком:
Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, делённый на свой аргумент:


Примечание: 
Теоремы о начальном и конечном значении (предельные теоремы):

Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, например, используется для анализа устойчивости траектории динамической системы.
Умножение на число:
Прямое и обратное преобразование Лапласа некоторых функций
Ниже представлена таблица преобразования Лапласа для некоторых функций.
Применения преобразования Лапласа
Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники:
Связь с другими преобразованиями
Фундаментальные связи
Практически все интегральные преобразования имеют схожую природу и могут получаться одно из другого через выражения соответствия. Многие из них являются частными случаями других преобразований. Далее даны формулы, связывающие преобразования Лапласа с некоторыми другими функциональными преобразованиями.
Преобразование Лапласа — Карсона
Преобразование Лапласа — Карсона получается из преобразования Лапласа путём домножения его на комплексную переменную:
Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа 
Преобразование Фурье
Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом 
Примечание: в этих выражениях опущен масштабирующий множитель 
Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.
Преобразование Меллина
Преобразование Меллина и обратное преобразование Меллина связаны с двусторонним преобразованием Лапласа простой заменой переменных. Если в преобразовании Меллина
положим 
Z-преобразование

где 

Связь выражается с помощью следующего соотношения:
Преобразование Бореля
Интегральная форма преобразования Бореля идентична преобразованию Лапласа, существует также обобщённое преобразование Бореля, с помощью которого использование преобразования Лапласа распространяется на более широкий класс функций.
Библиография
См. также
Ссылки
Примечания
Преобразование Абеля | Преобразования Бесселя | Преобразование Бушмана | Преобразование Гегенбауэра |Преобразование Гильберта | Преобразование Конторовича — Лебедева | Преобразование Лапласа | Преобразование Мейера | Преобразование Мелера — Фока | Преобразование Меллина | Преобразование Нерейна | Преобразование Радона | Преобразование Стильтьеса | Преобразование Фурье | Преобразование Ханкеля | Преобразование Хартли
Полезное
Смотреть что такое «Преобразование Лапласа» в других словарях:
преобразование Лапласа — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN Laplace transformLaplace transformation … Справочник технического переводчика
преобразование Лапласа — Laplace o transformacija statusas T sritis automatika atitikmenys: angl. Laplace s transform; Laplace s transformation vok. Laplace Transformation, f; Laplace Transformierung rus. преобразование Лапласа, n pranc. transformation de Laplace, f;… … Automatikos terminų žodynas
преобразование Лапласа — Laplaso transformacija statusas T sritis fizika atitikmenys: angl. Laplace transformation vok. Laplace Transformation, f rus. преобразование Лапласа, n pranc. transformation de Laplace, f … Fizikos terminų žodynas
Обратное преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия
обратное преобразование Лапласа — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN inverse Laplace transform … Справочник технического переводчика
Преобразование Фурье — Преобразование Фурье операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие … … Википедия
Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917 го года[1]. Важнейшее свойство преобразования Радона обратимость, то есть возможность… … Википедия
Преобразование Гегенбауэра — Преобразование Гегенбауэра интегральное преобразование функции : где многочлены Гегенбауэра. Если функция разлагается в обобщенный ряд Фурье по многочленам Гегенбауэра, то им … Википедия
Лапласа преобразование — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия
ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — трансформация Лапласа, в широком смысле интеграл Лапласа вида где интегрирование производится по нек рому контуру Lв плоскости комплексного переменного z, ставящий в соответствие функции f(z). определенной на L, аналитич. функцию… … Математическая энциклопедия