что такое периодичность функции
Периодические функции
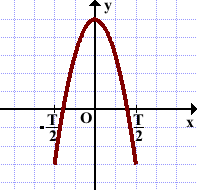
С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.
Дадим определение периодической функции:
Например, — периодические функции.
Для функций и период
Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:
1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения
График функции может выглядеть, например, вот так:
Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.
2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).
Построим график функции при
Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.
Период функции равен 2. Повторим периодически участок длины 2, который уже построен.
3. Найдите наименьший положительный период функции
Наименьший положительный период функции равен
График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).
Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции
4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции
Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.
Периодическая функция
Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).
Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:
Число T называют периодом функции y=f(x).
Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).
Свойства периодических функций
1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).
2) Для любого x из области определения y=f(x) если T1 — период функции, то
Так как T2 также является периодом функции y=f(x), то для аргумента x-T1
Следовательно, число T1+T2 является периодом функции y=f(x).
3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.
4) Если T — период функции f(x), то для аргумента kx+b
Значит число T/k — период функции f(kx+b).
5) Эти свойства следуют непосредственно из определения.
Например, для суммы f(x) и g(x):
Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.
Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.
Примеры периодических функций
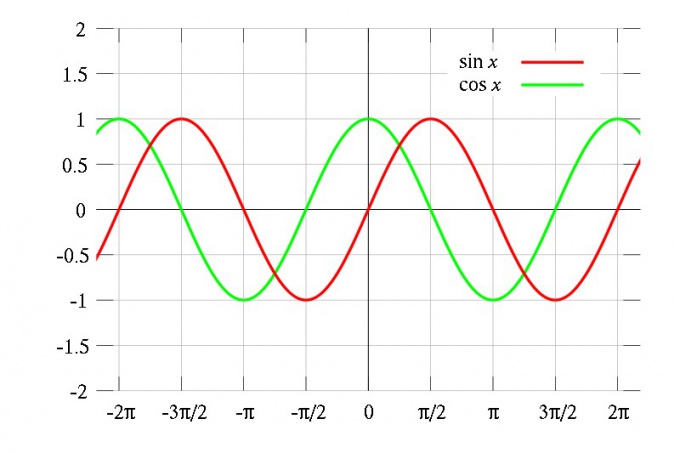
1) Поскольку для любого x выполняются равенства
то функции y=sin x и y=cos x являются периодическими с периодом T=2π.
2) Так как для любого x из области определения функции y=tg x выполняется равенство
tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.
Аналогично, y=ctg x — периодическая функция с периодом T=π.
3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.
Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.
4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.
Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.
Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.
5) Так как для любого действительного x и любого целого k выполняется равенство
Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y=
Главный период функций y=sin x и y=cos x T=2π.
Главный период функций y=tg x и y=ctg x T=π.
Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.
То есть любой период функции y=sin x имеет вид 2πn, n∈Z.
Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.
Таким образом, 2π — главный период функции y=sin x.
Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.
Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период
а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период
График периодической функции повторяется через промежутки длиной T (на оси Ox).
Дана часть графика
промежутке длиной T.
Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :
Как определить периодичность функции
Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.
Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.
Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.
Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.
Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.
Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.
Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.
Уроки математики и физики для школьников и родителей
суббота, 4 сентября 2021 г.
Урок 5. Периодичность тригонометрических функций
Из этого определения сразу следует, что если Т – период функции
– также периоды функций. Значит у периодической функции бесконечно много периодов.
Чаще всего (но не всегда) среди множества положительных периодов функции можно найти наименьший. Его называют основным периодом .
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
у = х – [х] , где [х] – целая часть числа. Если к произвольному значение аргумента этой функции добавить 1 , то значение функции от этого не изменится :
Следовательно, при любом значении х
sin (α + 360 ° ) = sin α
Таким образом, функции sin α и cos α от прибавления к аргументу α одного полного оборота ( 2π или 360 ° ) не меняют своих значений.
где k – любое целое число.
Следовательно, функции sin α и cos α – периодические.
Наименьшее положительное число, от прибавления которого к любому допустимому значению аргумента не изменяется значение функции, называется периодом функции.
В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным радиусом ОМ единичной окружности.
отсюда следует, что значения tg α и с tg α не изменяются, если к углу α прибавить любое число полуоборотов:
где k – любое целое число.
вычисляются по формуле
равен наименьшему числу, при делении которого на T 1 и T 2 получаются целые числа.
Найти период функции
не существует, так как такого числа, при делении которого на 2π и на 2 получались бы целые числа, нет.
Периода не существует.
Доказать следующее утверждение :
Так как тангенс – периодическая функция с минимальным периодом 20 ∙ 180 ° , то получим :
Доказать следующее утверждение :
Так как косинус – чётная и периодическая функция с минимальным периодом 2π , то получим :
сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.
Доказать следующее утверждение :
Так как синус – нечётная и периодическая функция с минимальным периодом 20 ∙ 360 ° , то получим :
Найти основной период функции
Пусть Т основной период функции, тогда:
так как 2 πk период синуса, то получим :
sin (7х + 7 t ) = sin (7х + 2 πk ),
Найти основной период функции
Пусть Т основной период функции, тогда:
со s 0,3х = со s 0,3(х + t ) = со s (0,3х + 0,3 t )
так как 2 πk период косинуса, то получим :
Найти период функции :
y = 5 sin 2 x + 2 ctg 3х.
Наименьшее число, при делении которого на
Найти период функции :
Находим периоды слагаемых. Период функции
Очевидно, что период заданной функции равен
Найти период функции :
Периода у заданной функции не существует, так как нет такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.
Найти период функции :
Приведём к общему знаменателю периоды :
Тогда наименьшее общее кратное (НОК) будет :
Теперь найдём период заданной функции :
Периодическая функция
Полезное
Смотреть что такое «Периодическая функция» в других словарях:
ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ — функция, значения которой не изменяются при прибавлении к аргументу некоторого (отличного от нуля) числа, т. н. периода функции. Напр., sin х периодическая функция с периодом 2?, ибо sin (х + 2?) = sin x при любых х. Широко применяются в… … Большой Энциклопедический словарь
периодическая функция — функция, значения которой не изменяются при прибавлении к аргументу некоторого (отличного от нуля) числа, так называемого периода функции. Например, sinx периодическая функция с периодом 2π, ибо sin(x + 2π) = sinx при любых x. Широко применяются … Энциклопедический словарь
периодическая функция — periodinė funkcija statusas T sritis fizika atitikmenys: angl. periodic function vok. periodische Funktion, f rus. периодическая функция, f pranc. fonction périodique, f … Fizikos terminų žodynas
ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ — функция, значения к рой не изменяются при прибавлении к аргументу нек рого (отличного от нуля) числа, т. н. периода функции. Напр., sin х П. ф. с периодом 2ПИ, ибо sin (х + 2ПИ) = sin x при любых х. Широко применяются в математике, физике и… … Естествознание. Энциклопедический словарь
ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ — ф ция, значения к рой не изменяются при прибавлении к аргументу нек рого (отличного от нуля) числа, т. н. периода ф ции. Напр., sinx П. ф. с периодом 2я, ибо sin (х + 2ПИ) = sinх при любых х. П. ф. широко применяются в математике, физике и… … Большой энциклопедический политехнический словарь
ПОЧТИ ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена обобщенным рядом Фурье. Существуют различные способы определения классов П. п. ф., основанные на понятиях замыкания, почти периода, сдвига. Каждый из классов П. п. ф. получается в результате замыкания в том… … Математическая энциклопедия