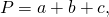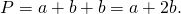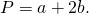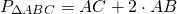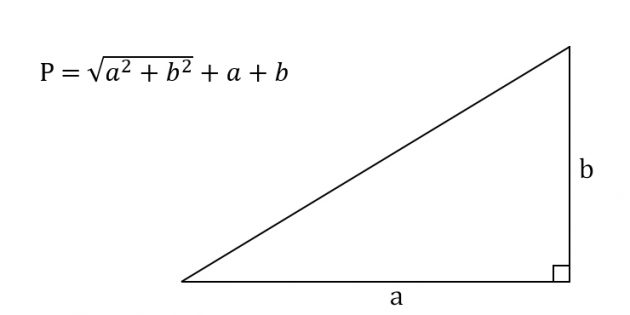что такое периметр равнобедренного треугольника
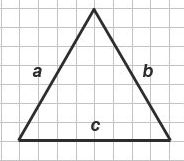
Периметр равнобедренного треугольника
Чтобы найти периметр равнобедренного треугольника, нужно знать всего две его стороны — основание и боковую сторону.
В общем случае формула для нахождения периметра треугольника выглядит так:
где a, b и c — длины сторон треугольника.
формулу можно упростить:
Таким образом, периметр равнобедренного треугольника равен сумме длин основания и удвоенной боковой стороны:
Соответственно, периметр равнобедренного треугольника ABC можно найти по формуле:
(здесь AC — основание, AB — боковая сторона).
1) Найти периметр равнобедренного треугольника, если его основание равно 4 см, а боковая сторона — 9 см.
Здесь а=4 см, b=9 см. По формуле Р=а+2b имеем: P=4+2∙9=22 (cм).
2) Периметр равнобедренного треугольника равен 170 см, а его основание — 60 см. Найти боковую сторону треугольника.
Здесь а=60 см, Р=170 см. По формуле Р=а+2b, 2b=Р-а, b=(Р-а):2, b=(170-60):2=55 (см).
Задача нахождения периметра равностороннего треугольника решается еще проще. Её мы рассмотрим в следующий раз.
Периметр равнобедренного треугольника

Всего получено оценок: 118.
Всего получено оценок: 118.
Периметр – это сумма длин всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.
Формула вычисления периметра
Боковые стороны равнобедренного треугольника равны между собой. Это вытекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и вытекает формула периметра:
P=2a+b, где b – это основание треугольника, a – значение боковой стороны.
Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон. Рассмотрим несколько задач на нахождение периметра равнобедренного треугольника. Задачи будем решать по мере возрастания сложности, это позволит лучше понять способ размышления, которому нужно следовать для нахождения периметра.
Задача 1
Высота равнобедренного треугольника, проведенная к основанию, является также медианой и биссектрисой. Это свойство очень часто используется при решении задач, связанных с равнобедренными треугольниками.
Треугольник АВС высотой ВM делится на два прямоугольных треугольника: АВM и ВСM. В треугольнике АВM катет ВM известен, катет АM равен половине основания треугольника АВС, так как ВM является медианой, биссектрисой и высотой. По теореме Пифагора найдем значение гипотенузы АВ.
Найдем периметр: P=AC+AB*2=6+5*2=16
Задача 2
Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.
Найдем AH через значение синуса:
$$sin (ABH)=
Выразим нужную сторону:
Через котангенс найдем значение AH:
$$AH=
Теперь, когда все требуемые значения найдены, определим периметр:
Задача 3
Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений
При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных. Попробуем решить по-другому.
Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a
Тогда основание будет равно: AC=AH+HC=AH*2=2a
С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято.
Подставим полученное значение в формулу площади.
Подставим значение a в формулу площади и определим значение высоты:
Через теорему Пифагора найдем боковую сторону треугольника:
Подставим значения в формулу периметра:
Что мы узнали?
Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.
Урок геометрии: как найти по формуле периметр треугольника
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых. Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю, дизайнеру.
Существуют разные способы найти периметр треугольника. Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Классическая формула
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Это интересно! Что значит вертикально и как выглядит вертикальная линия
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
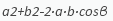
Далее рассчитывайте Р по такой формуле:
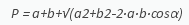
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Это интересно! Основы геометрии: что это такое биссектриса треугольника
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольнике является наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Это интересно! Изучаем символы: как обозначается в математике площадь
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
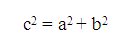
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
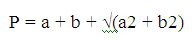
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
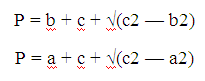
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
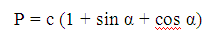
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
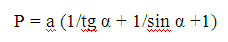
Это интересно! Как найти и чему будет равна длина окружности
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
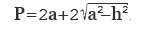
Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
Как найти периметр треугольника
Учимся находить периметр треугольника разными способами, а также тренируем полученные знания на примерах задач.
Периметр треугольника
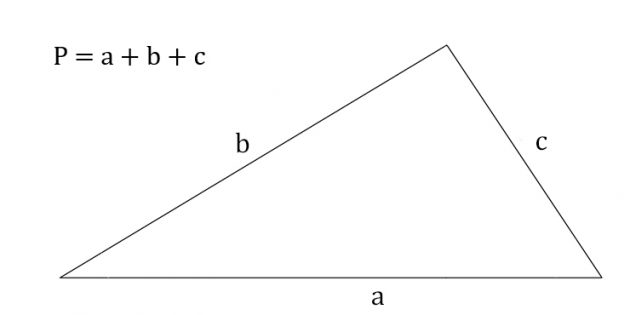
Периметр треугольника — это сумма длин всех его сторон.
Треугольник — это геометрическая фигура, которая состоит из трех точек (вершин), не лежащих на одной прямой. Эти точки попарно соединены тремя отрезками, которые называются сторонами (ребрами) многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Рассмотрим несколько способов нахождения периметра рассматриваемой фигуры. Каждая из предложенных формул опирается на те величины, которые нам уже известны.
Способы нахождения
По трем сторонам
Если мы уже знаем длину каждого ребра фигуры, расчет периметра будет проходить так:
где a, b и с — это стороны треугольника.
В случае, если нам известны стороны равнобедренного треугольника (у которого два ребра равны), формула для расчета периметра выглядит следующим образом:
где a — основание фигуры, а b и с — равные ребра.
Треугольник может также быть равносторонним (когда все стороны равны). Тогда P будем находить в соответствии с расчетами:
где a — это любая сторона фигуры.
По площади и радиусу вписанной окружности
Когда нам известна площадь данного многоугольника и радиус вписанной в него окружности, расчет P выглядит так:
где S — площадь фигуры, r — радиус вписанной в нее окружности.
По двум сторонам и углу между ними
Так как нам известен угол и две стороны, которыми он образован, мы можем найти третью сторону треугольника по теореме косинусов. И потом уже вычислить сумму длин всех ребер фигуры.
Теорема косинусов выглядит так:
где α — известный угол.
Тогда формула для расчета периметра всей фигуры в этом случае:
По боковой стороне и высоте (для равнобедренного)
Возвращаясь к свойствам равнобедренного треугольника, вспоминаем, что высота, проведенная к основанию треугольника из противоположной вершины, является одновременно высотой, биссектрисой и медианой. Это значит, что оба прямоугольных треугольника, которые она образует, равны между собой.
Формула для поиска периметра нашего равнобедренного будет опираться на теорему Пифагора. Пусть 1/2 основания (с) = d. Тогда:
где a — сторона равнобедренного треугольника и гипотенуза прямоугольного, h — высота равнобедренного и катет прямоугольного.
Не забываем, что d — это лишь половина основания равнобедренного треугольника, поэтому для поиска периметра результат нужно будет умножить на 2.
По двум катетам (для прямоугольного)
Еще раз вспомним теорему Пифагора для нахождения гипотенузы (обозначим ее буквой с).
где a и b — катеты треугольника.
Подставляем значение c в формулу для нахождения периметра и получаем:
Примеры решения задач
Для тренировки полученных знаний, рассмотрим несколько примеров решения задач на поиск периметра треугольника.
Задача №1
Какой P треугольника, если его стороны равны 6 см, 7 см и 3 см.
Решение:
Подставляем в формулу P = a+b+c известные величины и получаем: P = 6+7+3=16 см.
Задача №2
Известно, что основание равнобедренного треугольника равно 6 см, а его боковая сторона — 4 см. Найти P фигуры.
Решение:
Для данного случая подходит формула P=a+2b, подствляем значения: \(P=6+4\times2 = 14\) см.
Задача №3
Решение:
Задача №4
Дан равнобедренный треугольник. Нам известна его боковая сторона (4 см) и высота, опущенная к основанию (2 см). Нужно вычислить периметр фигуры.
Решение:
Задача №5
Дан прямоугольный треугольник с катетами 5 см и 7 см. Определить периметр фигуры.
Решение:
В формулу \(P=\sqrt
Нахождение периметра треугольника: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.
Формула вычисления периметра
Периметр (P) любого треугольника равняется сумме длин всех его сторон.
P = a + b + c
Периметр равнобедренного треугольника
Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:
P = a + 2b
Периметр равностороннего треугольника
Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:
P = 3a
Примеры задач
Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.
Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.
Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.
Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.