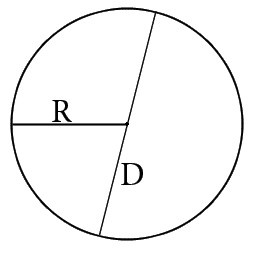
что такое периметр окружности
Длина окружности
6 класс, 9 класс, ЕГЭ/ОГЭ
Как найти длину окружности через диаметр
Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:
π— число пи — математическая константа, равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, равное 3,14
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, равное 3,14
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она всегда равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен 
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Онлайн калькулятор периметра круга. Как узнать длину круга, окружности.
Что такое длина окружности или периметр круга и как ее вычислить? Для того что бы это понять нам необходимо разобраться с тем чему равна длина окружности.
Длина окружности всегда равна числу π (Пи)
Давайте с вами разберемся что же такое число пи. Π – это постоянная величина равная 3,14159265…
Но обычно Пи приравнивают к 3,14 и это число используют для математических расчетов в которых не требуется оооооооооочень точное вычисление.
Откуда же взялось это число и почему оно всегда равно одному и тому же? Для того что бы нам понять что такое число пи нам необходимо разобрать простой пример. Допустим у нас имеется окружность с диаметром равному единицы, так вот длина окружности — это число «пи».
Иными словами Пи ≈ 3,14 диаметрам круга или окружности.
Теперь зная и понимая что такое π мы можем с легкостью высчитать периметр или длину окружности которая равна
P = D * π
или
P = 2 πR
где R –это радиус, а D – это диаметр
Формула периметра круга
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE
= 2 \cdot \pi \cdot r \]
\( P \) – периметр (длина окружности).
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки.
По формуле расстояния между двумя точками в заданной нами системе координат, получим:
Таким образом, мы и получаем, что уравнение (1) является уравнением окружности в декартовой системе координат.
Длина окружности (периметр круга)
Тогда, будем получать, что
Получаем, что отношение \( \frac<ρ><ρ'>=\frac<2τ> <2τ'>\) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \( n→∞ \) ), будем получать равенство:
Из последних двух равенств получим, что
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
Способы расчета периметра круга и длины окружности
Периметр круга — что это, определение
Круг — это геометрическое множество точек на плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит заданного неотрицательного числа.
Окружность — замкнутая кривая на плоскости, все точки которой равноудалены от центра окружности.
Эти определения плотно связаны друг с другом. Круг — это часть плоскости, ограниченная окружностью. Окружность — это граница круга.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Радиус — расстояние от центра окружности до любой ее точки. Это отрезок, который соединяет центр круга с его границей.
Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Он равен двум радиусам.
Периметр — это длина окружности, ограничивающей круг.
Понятия «периметр круга» и «длина окружности» считаются синонимичными.
Как рассчитать периметр круга или длину окружности
Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно \(\pi=3,14159. \)
Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:
Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.
Через радиус
Длину окружности L можно найти по формуле через радиус:
где \(\pi \) — число Пи, R — радиус.
Через диаметр
Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:
Примеры решения задач
Задача
Каков периметр круга, если его радиус равен 0,5 см?
Решение
Задача
Какова длина окружности, если ее диаметр равен 2 см?
периметр круга
Как найти периметр круга!? Формула периметра круга. Как на калькуляторе можно найти периметр круга!?
О периметре круга.
Формула периметра круга.
Начнем с формулы периметра круга.
Формула круга может выражаться через радиус.
Формула периметра круга через радиус.
Формула периметра круга через диаметр.
Также можно выразить периметр круга через диаметр. Поскольку мы занем, что диаметр = 2 радиуса, то в верхней формуле заменяем 2R на D.
Задача : найдите периметр круга если известен радиус.
Найдите периметр круга, если радиус круга равен 5см.
Вместо буквы R ставим наш радиус, и далее нам все нужно перемножить, на калькуляторе
Найденный периметр круга равен 31.4 см.
Задача : найдите диаметр круга, если известен периметр круга
Найдите диаметр круга, если известен периметр круга, который равен 94.2см.
Для того, чтобы найти периметр круга, нам нужно из формулы выразить диаметр через периметр, что будет выглядеть так :
Далее нам остается заменить букву P на значение из условия задачи 94.2см.
Если периметр круга равен 94.2см, то искомый диаметр равен 30см.
Периметр круга онлайн
Для того, чтобы найти периметр круга онлайн, нужно заполнить соответствующее поле :
В поле нужно напечатать значение радиуса круга.