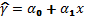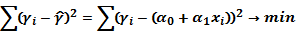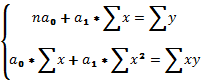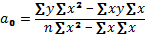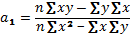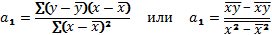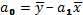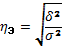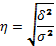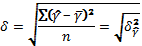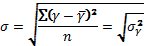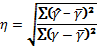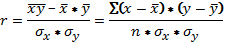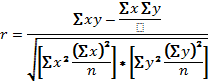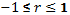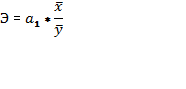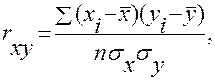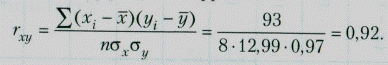что такое парная корреляция
Парная корреляция



Наиболее разработанной в теории статистики является методология однофакторного корреляционно-регрессионного анализа или парной корреляции, рассматривающей влияние вариации факторного признака x на результативный y.
Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление на основе анализа исходной информации соответствующей математической функции. Сложность заключается а том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований или осуществляется эмпирическим перебором и оценкой функций различных типов.
При изучении связи экономических показателей используют различные виды уравнения прямолинейной и криволинейных связей, внимание к линейным связям обеспечивается тем, что в большинстве случаев нелинейные формы для выполнения расчетов путем логарифмирования или замены переменных могут быть преобразованы в линейную форму.
Уравнение парной линейной корреляции имеет вид (9.1):
Где 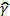
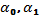
Поскольку 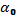
Коэффициент парной линейной регрессииa1 имеет смысл показателя силы связи между вариацией факторного признака x и вариацией результативного признака. Коэффициент показывает среднее значение изменения результативного признака y при изменении факторного признака x на одну единицу его измерения, т.е. вариацию y, приходящуюся на единицу вариации x. Знак a1 указывает направление этого изменения.
Параметры уравнения a0, a1 находятся методом наименьших квадратов, в основу которого положено требование минимальности сумм квадратов отклонений эмпирических данных y1 от теоретических 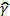
Для нахождения минимума данной функции ее частные производные приравниваются к нулю и решается следующая система нормальных уравнений (9.3):
Решение системы позволяет определить параметры уравнения регрессии. В общем виде параметры определяются следующим образом (9.4):
Параметры уравнения регрессии в ряде случаев удобно вычислять по следующим формулам, дающим тот же результат (9.5) и (9.6):
Рассчитанные таким образом значения a0 и a1 подставляются в уравнения регрессии.
Для практического использования моделей регрессии большое значение имеет их адекватность, т. е. соответствие фактическим статистическим данным. Корреляционный и регрессионный анализ зачастую проводится для небольшой по объему совокупности. Поэтому показатели регрессии и корреляции могут быть искажены действием случайных факторов, и требуется проверка адекватности модели.
При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют, насколько вычисленные параметры x характерны для отображения комплекса условий: не являются ли полученные значения параметров результатом, действия случайных причин.
Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n
Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определитьтесноту корреляционной связи между переменными x и y. Тесно-корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционным отношением 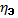
Где 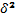
Говоря о корреляционном отношении как о показателе измерения тесноты зависимости от эмпирического корреляционного отношения следует отличать теоретическое. Теоретическое корреляционное отношение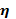
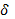
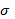
Тогда 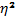
Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях стях между результативным и факторным признаками. Теоретическое корреляционное отношение часто называют индексом корреляции R. Корреляционное отношение может находиться в пределах от 0 до 1, т. е. 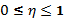
Где n – число наблюдений.
Для практических вычислений при малом числе наблюдений линейный коэффициент корреляции удобнее вычислять по формуле (9.17):
Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному и принимает значение в интервале (9.18):
Отрицательные значения указывают на обратную связь, положительные – на прямую. При r=0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее линейная связь между признаками. При 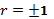
Несовпадение этих величин свидетельствует, что связь между изучаемыми признаками криволинейная. Установлено, что если разность квадратов η 2 и r 2 не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной.
Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных величин. Это вызывает необходимость проверки их существенности.
Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.
При линейной однофакторной связи t-критерий можно рассчитать по формуле (9.19):
гле (n-2) — число степеней свободы при заданном уровне значимости a и объеме выборки n.
После проверки адекватности построенной модели (уравнение регрессии) ее необходимо проанализировать, дать экономическую интерпретацию параметров регрессии. Прежде всего нужно проверить, согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак. Далее необходимо проанализировать значение параметра a1. Очевидно, что для линейной регрессии параметр a1 говорит о том, на сколько абсолютных единиц изменится результативный признак при изменении факторного на 1. Для удобства интерпретации параметра a1 используют коэффициент эластичности. Он показывает, на сколько процентов от его среднего значения изменится результативный признак при изменении факторного признака на 1% от его средней величины, и вычисляется по формуле (9.20):
Далее имеет смысл вычислить остатки 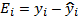
Пример. Методами корреляционного и регрессионного анализа требуется оценить зависимость производительности труда рабочих от стажа их работы по следующим исходным данным.
Что такое парная корреляция
Коэффициент парной корреляции R между результативным и факториальным признаками можно рассчитать по формуле [c.155]
Коэффициенты факторов можно найти и с помощью коэффициентов парной корреляции. [c.25]
Анализ проведенных расчетов по Миннефтепрому показал, что основное влияние на величину удельного расхода оказывают затраты времени на работы по проводке скважин t, Р Так, коэффициент парной корреляции Z/yz 0, 983. Это свидетельствует с достоверностью 0, 99 о наличии между ними линейной связи. Влияние же остальных двух факторов для данного объема наблюдений оказалось несущественным. Это подтвердилось и полученными значениями функции Фишера, характеризующими влияние факторов. (Методика использования критерия Фишера изложена в статье ( 1 ) этого же сборника). Соответствующее уравнение регрессии для Миннефтепрома имеет следующий вид [c.50]
Коэффициенты парной корреляции для линейной модели ( 1 ) [c.50]
Характерно, что коэффициенты парной корреляции для мо де— ли (10) оказались также ниже критического уровня для тех же самых объединений, что и в линейной модели. [c.52]
Коэффициенты парной корреляции для степенной модели (1О) [c.52]
Подводя итоги проведенному исследованию, следует отметить, что удобнее для практических расчетов является линейная модель, поэтому в этом смысле предпочтительными являются уравнения 4, 5, 6, 7, 8, 9 перед уравнениями 12, 13, 14, 15, 16, 17, хотя для уравнений 12—16 коэффициенты парной корреляции незначительно выше. [c.54]
В уравнении 16 коэффициент парной корреляции несколько ниже соответствующего коэффициента уравнения 9. [c.54]
В данной работе при построении динамических моделей также было проведено предварительное исследование многомерного временного ряда, вычислены коэффициенты взаимной корреляции и автокорреляции, коэффициенты парной корреляции и т. д. [c.59]
Кроме того, должны быть исключены краткосрочные (циклические колебания) и аномальные наблюдения, обеспечено достаточное число наблюдений по сравнению с количеством факторов и, наконец, должна отсутствовать парная корреляция между факторами (мультиколлинеарность). [c.138]
Линейный коэффициент парной корреляции (р) определяется по формуле [c.280]
Самая общая и типичная статистическая задача в экономическом анализе — изучение наличия, направления и интенсивности связей между показателями. Это первый этап познания закономерностей формирования результатов хозяйственной деятельности. Предположение о наличии и тесноте связи делается в случае выявления общих закономерностей в вариации значений изучаемых показателей. Источник возникновения этих общих закономерностей может быть разным — причинно-следственная связь между показателями, зависимость от общего фактора, случайное совпадение элементов вариации. Задача экономического анализа — раскрыть качественную основу взаимосвязи между количественными характеристиками экономических процессов. Стохастическое исследование связи происходит с помощью методов корреляционного анализа — коэффициентов и отношений корреляции. При этом в зависимости от характера исходной информации применяются разные приемы корреляционного анализа оценка парной корреляции между показателями с цифровой шкалой измерения ранговая корреляция и коэффициенты, рассчитанные по так называемым матрицам сопряженности для анализа связей между качественными показателями каноническая корреляция для анализа связи между группами показателей частная корреляция, которая позволяет исследовать связь между двумя [c.111]
Метод математического моделирования основан на построении однофакторной модели (парная корреляция) и многофакторной модели (множественная корреляция). [c.368]
Методы корреляционного и регрессионного анализа используются в комплексе. Наиболее разработанной в теории и широко применяемой на практике является парная корреляция, когда исследуются соотношения результативного признака и одного факторного признака. Это — однофакторный корреляционный и регрессионный анализ. Именно такой анализ является основой для изучения многофакторных стохастических связей. [c.70]
Использование способов парной корреляции для изучения стохастических зависимостей [c.129]
В заключение необходимо отметить, что мы рассмотрели использование способов парной корреляции только на двух примерах. Однако эта методика может быть использована для исследования соотношений между разными экономическими показателями, что позволяет значительно углубить знания об изучаемых явлениях, определить место и роль каждого фактора в изменении уровня исследуемого показателя. [c.137]
Изучая матрицы парных и частных коэффициентов корреляции, можно сделать вывод о тесноте связи между изучаемыми явлениями. Коэффициенты парной корреляции характеризуют тесноту связи между двумя показателями в общем виде с учетом взаимосвязей факторов, оказывающих воздействие на результативный показатель. [c.145]
Используя коэффициент парной корреляции, рассчитаем тесноту связи [c.273]
Величина коэффициента парной корреляции говорит о наличии тесной прямой связи между размером нераспределенной прибыли и инвестициями в основные фонды. [c.273]
Практическое значение ее в том, что есть системы, в которых среди всех факторов, влияющих на результативный признак, выделяется один важнейший фактор, который в основном определяет вариацию результативного признака. Измерение парных корреляций составляет необходимый этап в изучении сложных, многофакторных связей. Есть такие системы связей, при изучении которых следует предпочесть парную корреляцию. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связей для выполнения расчетов преобразуются в линейную форму. [c.238]
СТАТИСТИЧЕСКАЯ ОЦЕНКА НАДЕЖНОСТИ ПАРАМЕТРОВ ПАРНОЙ КОРРЕЛЯЦИИ [c.247]
Недостатком коэффициентов раздельной детерминации является их гетерогенный характер то, что они объединяют коэффициент парной корреляции, измеряющий нечистое влияние фактора, с р-коэффициентом, измеряющим условно чистое влияние фактора, [c.279]
Полученные коэффициенты парной корреляции между результативным признаком и каждым из факториальных призна ков по нефтедобывающим объединениям были близки к единице, что указывгло на очень высокую тесноту связи. [c.24]
Следует учесть, что коэффициенты парной корреляции показывают наличие тесной связи между производительностью труда и отдельными факторами и между факторами лишь в том случае, если различия между НГДУ по другим факторам (кроме учтенных) несущественны и незначительно влияют на произво- [c.80]
Критическое значение коэффициента парной корреляции при уровне значимости оС = 0,95 равно соответственно ZKpfab = 0,95) = 0,576 м при уровне значимости Q(, = = 0,98. равно Z/f/j/o 0,98) = 0,658 для объема выборки / = 10. Это свидетельствует об отсутствии линейной зависимости между фактическим удельным расходом и выбранными факторами для нашей выборки. Анализ данных по указанным объединениям показывает, что разброс фактических удельных расходов очень велик, что и послужило причиной низких значений коэффициентов парной корреляции. [c.51]
Оценка тесноты связи между переменными по коэффициенту парной корреляции не решает всех вопросов. В частности,этот показатель не учитывает частной («чистой») корреляции между изучаемь М явлением и характеризующими его факторами. Известно, что кФкУи аяся хорошая теснота связи между двумя показателями может возникнуть под влиянием третьего показателя, который имеет высокую теС»отУ связи с общими исследуемыми показателями. Чтобы исключить нежелательное влияние этих показателей и более достоверно установить зНачимость каждого фактора с учетом одновременного действия других, в0°Дят частный коэффициент корреляции разных степеней. Проверка надежности этого коэффициента по одному из известных критериев [21, 4Ь 46, 48] позволяет более точно оценить значимость каждого фактора, выбранного для модели. Необходимо оценить существенность факторов в зависимости от характера связи между ними, а также между отдельными факторами и исследуемым показателем. [c.17]
В табл. 4 представлена матрица парных коэффициентов корреляции. Анализ представленных в табл. 4 данных показывает, что между отдельными факторами имеется мультиколлениарность. Так, между факторами Xj и 3f коэффициент парной корреляции превышает 0,8. Из этого следует, что один из указанных в паре факторов должен быть исключен при дальнейшем анализе. Решение о том, какой фактор необходимо исключить, принимает исследователь, основываясь на результатах предшествующего анализа о значимости каждого фактора. В данном случае целесообразно исключить фактор «X. [c.28]
Далее была проведена проверка факторов на мультиколлениарность [51]. На основании вычисленных коэффициентов парной корреляции факторы были включены в модель. Только после этого перешли к исследованию характера изменения параметров модели во времени и к выбору оптимальной формы связи. Для этого весь массив был разбит на подмас-сивы. [c.59]
Смотреть страницы где упоминается термин Парная корреляция
Смотреть главы в:
Парная корреляция
Парная корреляция позволяет оценить тесноту связи между двумя признаками. Для выявления корреляционной связи между двумя признаками можно построить поле корреляции.
Расположение точек на поле корреляции позволяет судить о наличии и о характере связи (нелинейная, а если линейная, то и о направлении (прямая или обратная)).
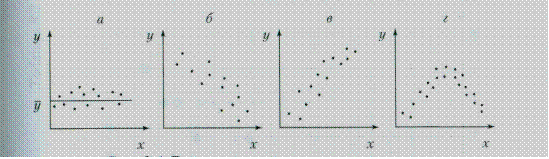
На рис. 1.1 показаны основные возможные способы расположения точек поля корреляции. Если точки поля корреляции располагаются в определенном направлении, то можно предположить наличие связи.
Рис. 1.1. Возможное расположение точек поля корреляции (х; у):
а – корреляция отсутствует; б – корреляция линейная обратная;
Пример 1.1. Изучается зависимость оценки, полученной на экзамене (у) 8 студентами, от суммы баллов (х), набранных ими в течение семестра. Данные приведены в табл. 1.1.
| Номер студента | Оценка на экзамене (у) | Сумма баллов (х) |
Для построения поля корреляции в координатных осях:
— на оси Х отложим значения баллов х, набранных студентами в течение семестра;
— на оси У покажем значения оценки у, полученной на экзамене студентами;
— нанесем точки с координатами (х; у) для каждого студента.
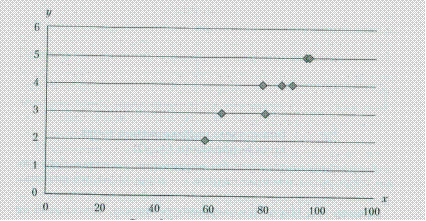
На рис. 1.2 показано поле корреляции. Расположение точек позволяет предположить, что существует прямая линейная связь между оценкой, полученной на экзамене (у) студентами, и суммой баллов (х), полученных ими в течение семестра.
Рис. 1.2. Поле корреляции
Теснота линейной связи измеряется коэффициентом парной корреляции:
где 



Если знаки отклонений от средних совпадают, то связь прямая 
если знаки отклонений не совпадают, то связь обратная 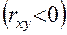

Чем ближе значение 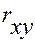
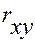
Характеризовать тесноту связи поможет следующая таблица:
| Коэффициент корреляции | Характеристика связи |
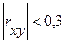 | Слабая |
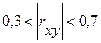 | Средняя |
 | Сильная или тесная |
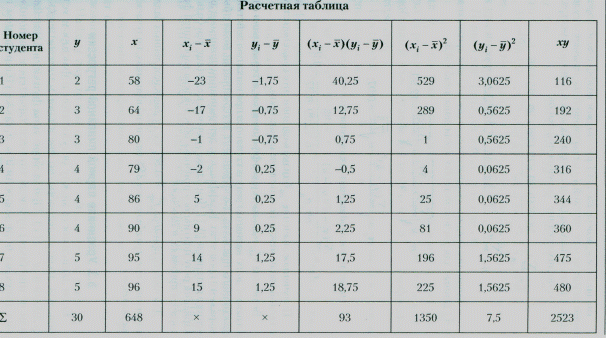
По данным примера табл. 1.1 рассчитаем коэффициент парной корреляции между оценкой (у), полученной на экзамене студентами, и суммой баллов (х), полученных ими в течение семестра:
— вычислим средние значения признаков:
— вычислим средние квадратические отклонения признаков 

данные для расчета которых приведены в табл. 1.2:
— вычислим коэффициент корреляции:
Полученное значение 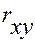
Величина 
Для нашего примера