что такое параксиальная область

Параксиальная оптика — Понятие параксиальная область

Как уже говорилось выше, параксиальная оптика неразрывно связана с параксиальной областью. Необходимо конкретизировать понятие «параксиальная область». Утверждение, что это область бесконечно приближенная к оптической оси несколько размыто. Хотелось бы максимально точно определить «размеры» параксиальной области. Для этого вначале необходимо ближе ознакомится с самой распространенной формой поверхности, разделяющей области с различными коэффициентами преломления.

Итак, знакомьтесь – сфера. Я думаю, для многих читателей не секрет, что подавляющее число линз являются сферическими (сферическая линза). Дам свое (не оптическое) определение сферической линзы:

Двояковыпуклая сферическая линза – кусок стекла, ограниченный двумя сферами.

Приведу пример построения положительной двояковыпуклой линзы. Изначально у нас есть прямоугольный параллелепипед стекла подходящего размера (рисунок 1).

Рисунок 1. Стеклянная заготовка.

У нашей линзы должно быть две (как минимум одна) выпуклых сферических поверхности. Ограничим нашу стеклянную заготовку сферой с одной стороны (рисунок 2).

Рисунок 2. Стеклянная заготовка ограниченная одной сферой.

Затем сделаем то же самое с другой стороной заготовки (рисунок 3).

Рисунок 3. Стеклянная заготовка ограниченная двумя сферами.

Обрежем все лишнее – удалим «куски стекла» не вошедшие в область пересечения двух сфер (рисунок 4).

Рисунок 4. Линза ограниченная двумя сферами.

В итоге мы получим желаемую двояковыпуклую линзу со сферическими поверхностями (рисунок 5).

Рисунок 5. Двояковыпуклая линза со сферическими поверхностями.

Так какая же связь между этой линзой и параксиальной областью? Для ответа на этот вопрос придется рассмотреть несколько формул.

Сферическая поверхность, центр которой находится в начале координат, задается следующей формулой:

Нам же необходимо рассмотреть случай, когда центр сферической поверхности находится на оптической оси (ось ), а сама поверхность проходит через начало координат. Тогда формулу (1) можно записать в следующем виде:

Для того чтобы не таскать за собой лишние переменные несколько упростим формулу (2) заменив на :

После такой подстановки будем иметь:

Раскроем скобки и упростим выражение до следующего вида:

Решим квадратное уравнение относительно и получим:

Этому решению соответствует рисунок 6.

Нас интересует только первая точка пересечения. Решением для этой точки является выражение (5) со знаком минус:

(6)

Вынесем R за скобки:

Заменим радиус сферы R на кривизну определяемую следующим выражением:

В результате получим:

Применим несколько простых математических преобразований. Честно говоря, я сомневался, стоит ли их тут приводить. Может, хватило бы конечного результата? Но все-таки решил немного облегчить Вам жизнь и расписал:

Таким образом, решение для z выглядит так:

Выражение (11) описывает сферу заданного радиуса. Но для определения параксиальной области нам нужно рассмотреть выражение (9). А если точнее, то его сначала следует привести к такому виду:

А затем разложить корень в правой части равенства в степенной ряд:

И, наконец, выражение для z:

А вот отсюда уже следует вывод:

Параксиальная область – область, в которой любая отражающая или преломляющая поверхность может быть описана первым членом степенного ряда (14).

Это значит, что для определения z в параксиальной области для расчета будет использоваться следующая формула:

Кроме того, нужно отметить, что мы будем ограничивать протяженность поверхностей объекта или изображения слагаемыми, которые пропорциональны квадрату величины объекта или изображения. Вдобавок, мы будем полагать, что любые углы, которые мы будем встречать при расчете, настолько малы, что их значение в градусах будет равно их же значению в радианах. Если принимать во внимание эти условия, то можно показать, что в параксиальной области любая поверхность находящееся в пространстве предметов идеально отображается в пространстве изображений.

Источник

Параксиальный луч

Параксиа́льный луч (нулевой луч) — одно из основных понятий, так называемой, параксиальной оптики (или как её часто называют оптики Гаусса).

Нулевыми, или параксиальными, лучами называются лучи, лежащие бесконечно близко к оптической оси центрированной оптической системы, или под весьма малыми углами к ней, и образующие на всех оптических поверхностях бесконечно малые углы падения и преломления. То есть, можно сказать, что параксиальным лучом будет луч, проходящий внутри бесконечно узкого цилиндра, окружающего оптическую ось системы.

Данное понятие геометрической оптики введено для удобства определения положения кардинальных точек центрированной оптической системы и её фокусных расстояний, так как в этом случае синусы и тангенсы углов, образуемых лучами с осью, могут заменять друг друга и, кроме того, могут быть заменены значениями углов в радианах.

Область, в пределах которой можно производить такие замены, принято называть нулевой, или параксиальной областью.Формулы, выведенные для этой области на основе нулевых лучей, имеют простую математическую форму.

В практике оптических расчётов параксиальные и нулевые лучи иногда различают, понимая под параксиальным лучом частный случай реального луча, а под нулевым лучом — условный (фиктивный) луч, преломляющийся не на преломляющих поверхностях, а на условных плоскостях, и засекающий на оптической оси отрезки луча параксиального.

См. также

Литература

Полезное

Смотреть что такое «Параксиальный луч» в других словарях:

параксиальный луч — Луч, идущий на малом расстоянии от оптической оси системы и под малым углом к ней. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики физическая оптика… … Справочник технического переводчика

параксиальный луч — gretaašis spindulys statusas T sritis fizika atitikmenys: angl. Gauss ray; paraxial ray vok. paraxialer Strahl, m; Paraxialstrahl, m rus. гауссов луч, m; параксиальный луч, m pranc. rayon de Gauss, m; rayon paraxial, m … Fizikos terminų žodynas

гауссов луч — gretaašis spindulys statusas T sritis fizika atitikmenys: angl. Gauss ray; paraxial ray vok. paraxialer Strahl, m; Paraxialstrahl, m rus. гауссов луч, m; параксиальный луч, m pranc. rayon de Gauss, m; rayon paraxial, m … Fizikos terminų žodynas

ОПТИЧЕСКИЙ РЕЗОНАТОР — устройство, в к ром могут возбуждаться стоячие или бегущие эл. магн. волны оптич. диапазона. О. р. представляет собой совокупность неск. зеркал и явл. открытым резонатором, в отличие от большинства объёмных резонаторов, применяемых в диапазоне… … Физическая энциклопедия

КАРДИНАЛЬНЫЕ ТОЧКИ ОПТИЧЕСКОЙ СИСТЕМЫ — точки на оси ОО (рис.) центрированной оптич … Физическая энциклопедия

Gauss ray — gretaašis spindulys statusas T sritis fizika atitikmenys: angl. Gauss ray; paraxial ray vok. paraxialer Strahl, m; Paraxialstrahl, m rus. гауссов луч, m; параксиальный луч, m pranc. rayon de Gauss, m; rayon paraxial, m … Fizikos terminų žodynas

Paraxialstrahl — gretaašis spindulys statusas T sritis fizika atitikmenys: angl. Gauss ray; paraxial ray vok. paraxialer Strahl, m; Paraxialstrahl, m rus. гауссов луч, m; параксиальный луч, m pranc. rayon de Gauss, m; rayon paraxial, m … Fizikos terminų žodynas

gretaašis spindulys — statusas T sritis fizika atitikmenys: angl. Gauss ray; paraxial ray vok. paraxialer Strahl, m; Paraxialstrahl, m rus. гауссов луч, m; параксиальный луч, m pranc. rayon de Gauss, m; rayon paraxial, m … Fizikos terminų žodynas

paraxial ray — gretaašis spindulys statusas T sritis fizika atitikmenys: angl. Gauss ray; paraxial ray vok. paraxialer Strahl, m; Paraxialstrahl, m rus. гауссов луч, m; параксиальный луч, m pranc. rayon de Gauss, m; rayon paraxial, m … Fizikos terminų žodynas

paraxialer Strahl — gretaašis spindulys statusas T sritis fizika atitikmenys: angl. Gauss ray; paraxial ray vok. paraxialer Strahl, m; Paraxialstrahl, m rus. гауссов луч, m; параксиальный луч, m pranc. rayon de Gauss, m; rayon paraxial, m … Fizikos terminų žodynas

Источник

Параксиальный пучок лучей

Смотреть что такое «Параксиальный пучок лучей» в других словарях:

ПАРАКСИАЛЬНЫЙ ПУЧОК ЛУЧЕЙ — света, пучок лучей, распространяющихся вдоль оси центрированной оптич. системы и образующих очень малые углы с осью и нормалями к преломляющим и отражающим поверхностям системы. Осн. соотношения, описывающие образование изображений оптических в… … Физическая энциклопедия

ПАРАКСИАЛЬНЫЙ ПУЧОК ЛУЧЕЙ — света(от греч. para возле и лат. axis ось) пучок лучей, распространяющихсявдоль оси центрированной оптич. системы и образующих очень малые углы сосью и нормалями к преломляющим и отражающим поверхностям системы. Осн … Физическая энциклопедия

ПАРАКСИАЛЬНЫЙ ПУЧОК — (от пара. и лат. axis ось) пучок лучей, образующий с оптической осью системы малый угол … Большой Энциклопедический словарь

параксиальный пучок — (от пара. и лат. axis ось), пучок лучей, образующий с оптической осью системы малый угол. * * * ПАРАКСИАЛЬНЫЙ ПУЧОК ПАРАКСИАЛЬНЫЙ ПУЧОК (от пара. (см. ПАРА. (приставка или часть сложных слов)) и лат. axis ось), пучок лучей, образующий с… … Энциклопедический словарь

ПАРАКСИАЛЬНЫЙ ПУЧОК — (от пара. и лат axis ось), пучок лучей, образующий с оптич. осью системы малый угол … Естествознание. Энциклопедический словарь

Линза (в оптике) — Линза (нем. Linse, от лат. lens чечевица), прозрачное тело, ограниченное двумя поверхностями, преломляющими световые лучи; является одним из основных элементов оптических систем. Наиболее употребительны Л., обе поверхности которых обладают общей… … Большая советская энциклопедия

Линза — I Линза (нем. Linse, от лат. lens чечевица) прозрачное тело, ограниченное двумя поверхностями, преломляющими световые лучи; является одним из основных элементов оптических систем (См. Оптические системы). Наиболее употребительны Л., обе… … Большая советская энциклопедия

АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ — (от лат. aberratio уклонение), искажения, погрешности изображений, формируемых оптич. системами. А. о. С, проявляются в том, что оптич. изображения не вполне отчётливы, не точно соответствуют объектам или оказываются окрашенными. Наиболее… … Физическая энциклопедия

Плоскопараллельная пластинка — ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения (См. Оптическое излучение). Оптическая длина пути луча света в П. п. nd [d геометрическая толщина П. п., n … Большая советская энциклопедия

Источник

Параксиальная или гауссова оптика

В параксиальной области (бесконечно близко к оптической оси), любая реальная система ведёт себя как идеальная.

Линейное увеличение ОС—это отношение линейного размера изображения в направлении, перпендикулярном оптической оси, к соответствующему размеру предмета в направлении перпендикулярном оптической оси.

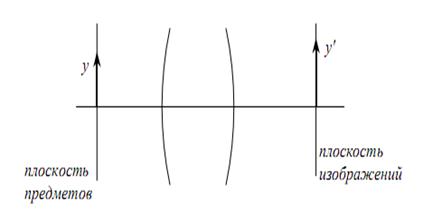
Если В>0 то отрезки у и у/ направлены в одну сторону, если В 1 то величина изображения больше величины предмета.

Рисунок 13. Сопряжённые линейные величины

Угловое увеличение оптической системы –это отношение тангенса угла между лучом и оптической осью в пространстве изображений к тангенсу угла между сопряжённым с ним лучом в пространстве предметов и осью.

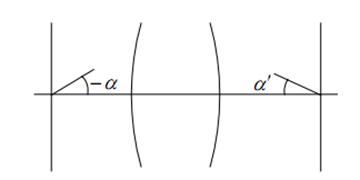
Рисунок 14. Сопряжённые угловые величины

Продольное увеличение-отношение бесконечно малого отрезка, взятого в вдоль оптической оси в пространстве изображений, к сопряжённому с ним отрезку в пространстве предметов.

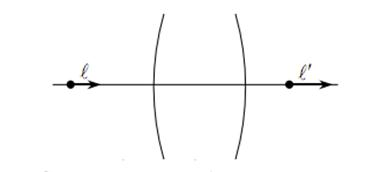
Рисунок 15. Сопряжённые продольные величины

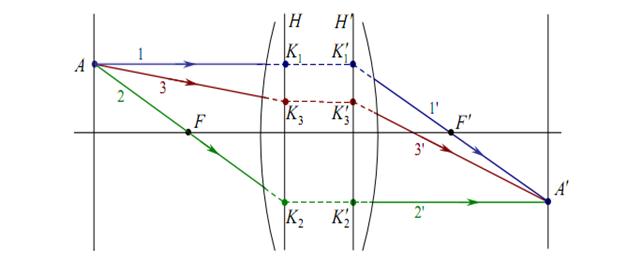
Кардинальные точки и отрезки:

Главными плоскостями системыназывается пара сопряжённых плоскостей, в которых линейное увеличение равно единице.

Главные точки Н и Н’ –это точки пересечения главных плоскостей с оптической осью.

Рассмотрим случай, когда линейное увеличений равно нулю или бесконечности. Отодвинем плоскость предметов бесконечно далеко от оптической системы. Сопряжённая ей плоскость плоскость задней фокальной плоскостью, а точка пересечения этой плоскости с оптической осью— задний фокус F’.

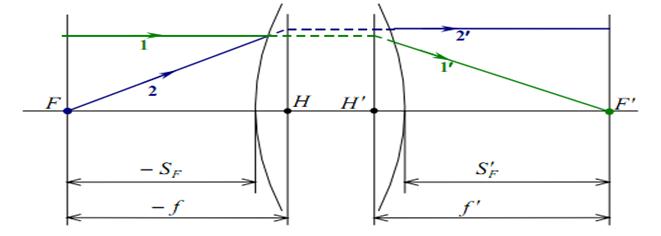
Рисунок 16. Кардинальные точки и отрезки

Заднее фокусное расстояниее f’это расстояние от задней главной точки до заднего фокуса.

Задний фокальный отрезок S’_F это расстояние от последней поверхности до заднего фокуса.

Система называется собирающей или положительной если f’>0,

Система называется рассеивающей или отрицательнойесли f’

Рисунок 19. Схема построения точки

Источник

Что такое параксиальная область

Ограничения пучков в оптических системах связаны с конечностью физических размеров оптических элементов. Эти ограничения обозначаются на схемах и чертежах в виде диафрагм, роль которых могут играть оправы линз, а также отдельно стоящие диафрагмы.

В принципе диафрагмы могут рассматриваться не только для реальных, но и для нулевых лучей (то есть в параксиальной области). Как правило, в первом приближении анализ габаритов пучков производится в параксиальной области, но впоследствии расчеты обязательно уточняют с использованием реальных лучей.

7.2.1. Апертурная диафрагма

Ограничение размера пучков – результат совместного действия всех имеющихся в оптической системе диафрагм. Однако можно выделить одну (наименьшую) диафрагму, и считать, что остальные не ограничивают ход лучей. Такая диафрагма называется апертурной (рис.7.2.1).

Апертура (лат. – отверстие) – это понятие, которое в геометрической оптике определяет размер пучка лучей.

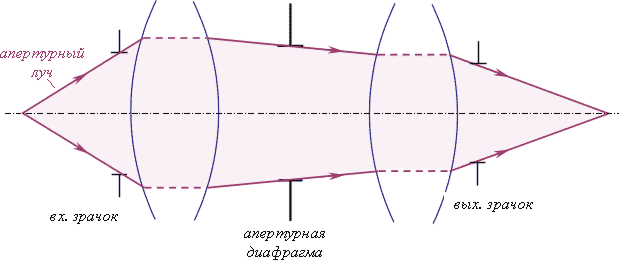
Рис.7.2.1. Апертурная диафрагма.

Апертурная диафрагма – это диафрагма, которая ограничивает размер осевого пучка (идущего из осевой точки предмета).

Рассмотрим апертурную диафрагму и предшествующую ей часть оптической системы:

Если апертурная диафрагма находится в пространстве предметов, то входным зрачком является сама апертурная диафрагма.

Выходной зрачок – это параксиальное изображение апертурной диафрагмы в пространстве изображений, сформированное последующей частью оптической системы в прямом ходе лучей.

Если апертурная диафрагма находится в пространстве изображений, то выходным зрачком является сама апертурная диафрагма.

Входной зрачок, выходной зрачок и апертурная диафрагма сопряжены. Апертурный луч внутри системы проходит через край апертурной диафрагмы, в пространстве предметов – через край входного зрачка, а в пространстве изображений – через край выходного зрачка.

Главный луч – это луч, идущий из внеосевой точки предмета и проходящий через центр апертурной диафрагмы.

По законам параксиальной оптики главный луч также проходит через центр входного зрачка в пространстве предметов и через центр выходного зрачка в пространстве изображений (рис.7.2.2).

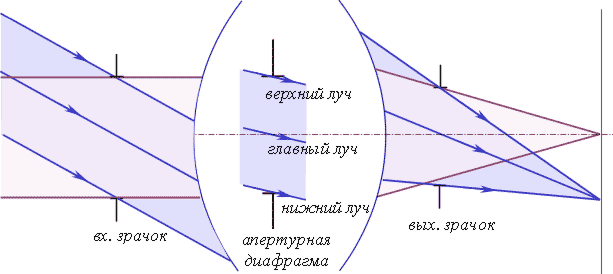
Рис.7.2.2. Внеосевой пучок.

Верхний луч внеосевого пучка – это луч, проходящий через верхний край апертурной диафрагмы и соответствующие ему сопряженные точки входного и выходного зрачков.

Нижний луч внеосевого пучка – это луч, проходящий через нижний край апертурной диафрагмы и соответствующие ему сопряженные точки входного и выходного зрачков.

Чтобы определить, какая из диафрагм оптической системы является апертурной, надо найти изображение всех диафрагм в пространстве предметов в обратном ходе по законам параксиальной оптики.

Апертурная диафрагма – это диафрагма, изображение которой видно под наименьшим углом из осевой точки предмета.

Если предмет находится на бесконечности, то апертурная диафрагма – это диафрагма, изображение которой имеет наименьшие линейные размеры.

Определению положений и размеров зрачков и построению хода апертурного и главного луча посвящена лабораторная работа «Ограничение пучков лучей в оптических системах».

Решение задач на построение хода апертурного и главного лучей, нахождение апертурной диафрагмы и определение положения и размера зрачков рассматривается в практическом занятии «Расчет положений зрачков на основании данных об апертурной диафрагме для различных типов оптических систем».

7.2.2. Полевая диафрагма

Поле – это часть плоскости предметов, которая изображается оптической системой. В параксиальной оптике размер поля неограничен. В реальной оптической системе поле ограничивается полевой диафрагмой.

Полевая диафрагма – это диафрагма, ограничивающая размеры поля.

Полевая диафрагма располагается либо на поверхности предмета, либо на поверхности изображения, либо в плоскости промежуточного изображения. Изображения полевой диафрагмы через соответствующие части оптической системы называются входными и выходными люками (окнами) (рис.7.2.3).

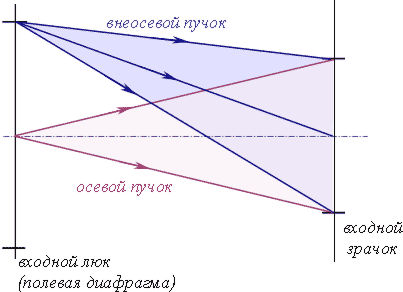
Рис.7.2.3. Полевая диафрагма.

7.2.3. Виньетирование

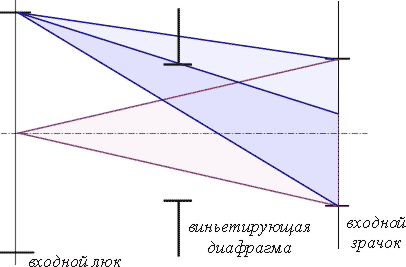
Рис.7.2.4. Виньетирование.

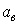
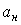
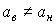
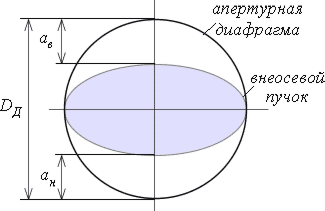
В общем случае область диафрагмы выглядит так, как показано на рис.7.2.5, из которого видно, что пучок срезается сверху на величину , и снизу на величину . Эти величины могут быть равны друг другу, тогда виньетирование симметрично. Если – виньетирование несимметрично.

Рис.7.2.5. Виньетирование (плоскость апертурной диафрагмы).

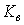
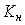
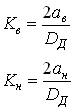
Коэффициент виньетирования – это отношение размеров срезаемой части диафрагмы к ее радиусу. Коэффициенты виньетирования сверху и снизу вычисляются следующим образом:

(7.2.1)

Внеосевой пучок лучей в случае виньетирования показан на рис.7.2.6.

Рис.7.2.6. Виньетированный пучок лучей.

Источник