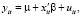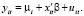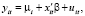что такое панельные данные

Объединённая модель панельных данных

Материал из MachineLearning.

Панельные данные состоят из наблюдений одних и тех же экономических единиц, которые осуществляются в последовательные периоды времени. Панельные данные насчитывают три измерения: признаки (переменные) – объекты – время. Для них разработаны специальные методы анализа.

Содержание

Введение

Панельные данные (Panel data)

Для большинства баз панельных данных характерно, что они содержат наблюдения о большом количестве объектов за относительно короткий промежуток времени.

Панельные данные ценны для экономистов тем, что при правильном их анализе можно избавиться от влияния индивидуальных особенностей объектов (individual heterogeneity), которые, как правило, являются одной из серьезнейших проблем анализа однократных данных.

Примеры использования моделей панельных данных

Пример 1. Макроэкономика. Объекты – страны; – характеристики (например, инфляция, объем инвестиций, объем экспорта, импорта); – показатель ВВП на душу населения. Хотим выяснить, как он зависит от приведенных показателей.

Пример 2. Микроэкономика. Объекты – домашние хозяйства; – доход, число человек в семье, недвижимость, количество иждивенцев в семье, образование, возраст, пол; – структура расходов. Данная задача часто возникает в маркетинге, когда необходимо выяснить каков рынок тех или иных товаров.

Пример 3. Объекты – выборка телезрителей ; – доход, образование, возраст, пол; – структура просмотров:

Пример 4. Объекты – коммерческие фирмы; – оборот, прибыль, число сотрудников, отрасль; – рыночная стоимость.

Пример 5. (См. Экономика преступления: теоретическое и эмпирическое исследование определяющих факторов преступности) Методы анализа панельных данных эффективны для мониторинга и анализа преступлений. Приведем одну из постановок задач в данном контексте. Объекты – регионы; – уровень жизни, среда и ресурсы, демография и миграции, политика, экономика и социальная сфера, культура, образование, внешние условия; – индекс конфликтов.

Обозначения

Здесь – векторы, – матрица.

Преимущества анализа панельных данных перед другими методами

Благодаря специальной структуре панельные данные позволяют строить более гибкие и содержательные модели и получать ответы на вопросы, которые недоступны только в рамках, например, моделей, основанных на пространственных данных.

Основные модели анализа панельных данных

Описание объединенной модели

Простейшая модель – это обычная линейная модель регрессии

или в матричной форме

В эконометрической литературе данная модель носит название объединенной модели регрессии (pooled model).

Источник

Что такое панельные данные

8. Классификация видов эконометрических переменных и типов данных. Проблемы, связанные с данными

В эконометрических моделях в основном используются данные трёх типов:

1) пространственные данные (cross-sectional data);

2) временные ряды (time-series data);

3) панельные данные (panel data).

Пространственными данными называется совокупность экономической информации, которая характеризует различные объекты, однако полученной за один и тот же период или момент времени.

Пространственные данные являются выборочной совокупностью из некоторой генеральной совокупности. Примером пространственных данных может служить комплекс экономической информации по какому-либо предприятию (численность работников, объём производства, размер основных фондов), объёмах потребления продукции определённого вида, данные о ВВП различных стран в каком-либо конкретном году и т. д.

Временными данными называется совокупность экономической информации, которая характеризует один и тот же объект, но за разные периоды времени.

Отдельно взятый временной ряд можно рассматривать как выборку из бесконечного ряда значений показателей во времени. Примером временных данных могут служить данные о динамике индекса потребительских цен, ежедневные обменные курсы валют.

Отличия временных данных от пространственных данных:

1) единицы временных рядов подвержены явлению автокорреляции (зависимости между прошлыми и текущими наблюдениями временного ряда), т. е. они не являются статистически независимыми в отличие от единиц случайной пространственной выборки;

2) единицы временных рядов не являются одинаково распределёнными величинами;

3) в отличие от пространственных данных временные данные естественным образом упорядочены во времени.

Панельными данными называются данные, содержащие сведения об одном и том же множестве объектов за ряд последовательных периодов времени.

Панельные данные являются обобщением или комбинацией пространственных и временных данных. Примером панельных данных могут служить показатели хозяйственной деятельности совокупности предприятий, которые собираются каждый год. В этом случае мы получим массив данных, в котором содержатся и данные об однородных объектах за один и тот же период времени, и последовательные значения одной экономической переменной в различные периоды времени. Но если совокупность предприятий из года в год будет различна, то такие данные уже не будут панельными.

Набором признаков называется совокупность экономической информации, которая характеризует изучаемый процесс или объект.

Признаки взаимосвязаны между собой, и при этом они могут выступать в одной из двух ролей:

1) в роли результативного или зависимого признака;

2) в роли факторного или независимого признака.

В эконометрических моделях результативный признак называется объясняемой переменной, а факторный признак называется объясняющей переменной.

В эконометрическом моделировании выделяют следующие виды экономических переменных:

1) экзогенные или независимые переменные (х), значения которых задаются извне. В определённой степени экзогенные переменные поддаются управлению;

2) эндогенные или зависимые переменные (у), значения которых определяются внутри модели;

3) лаговые переменные – это экзогенные или эндогенные переменные, которые относятся к предыдущим моментам времени и находятся в эконометрической модели одновременно с переменными, относящимися к текущему моменту времени. Например, xt-1 – это лаговая экзогенная переменная, а yt-1 – это лаговая эндогенная переменная;

4) предопределённые или объясняющие переменные – это лаговые (xt-1) и текущие (х) экзогенные переменные, а также лаговые эндогенные переменные (yt-1).

5) фиктивные переменные используются в эконометрических моделях для характеристики явления или процесса, в отношении которого нет данных по качественному признаку;

6) переменные-заместители искусственно вводятся в эконометрическую модель для характеристики явления или процесса, который не может быть количественно охарактеризован. При этом переменная-заместитель тесно коррелирует с этим явлением.

В эконометрических исследованиях большое внимание уделяется проблеме данных, т. е. специальным методам работы при наличии данных с пропусками, влиянию агрегирования данных на эконометрические измерения. Зачастую по единицам исследуемой совокупности информация отсутствует, а в наличии имеются данные, характеризующие более крупные единицы (агрегаты). Следует отметить, что при агрегировании временных данных опасность искажения результатов измерений гораздо больше, чем при агрегировании пространных данных, потому что с одной стороны, добавляется эффект автокорреляции, а с другой – происходит погашение случайной компоненты.

Источник

ПАНЕЛЬНЫЕ ДАННЫЕ.

Согласно проведенным исследованиям, панельные данные представляют собой прослеженные во времени пространственные выборки, которые состоят из наблюдений одних и тех же экономических объектов в последовательные периоды времени. Они ценны для экономистов тем, что при правильном их анализе можно избавиться от влияния индивидуальных особенностей объектов которые, как правило, являются одной из серьезнейших проблем анализа однократных данных. Целью данной работы является углубить знания в области анализа панельных данных. Для этого в работе последовательно рассмотрены основные преимущества и проблемы панельных данных, основные регрессионные модели и практический пример использования панельных данных.

Основные преимущества данных этого типа заключаются в следующем:

1) они предоставляют исследователю большое количество наблюдений, увеличивая число степеней свободы и снижая коллинеарность между объясняющими переменными и, следовательно, улучшая эффективность оценок;

2) они позволяют анализировать множество важных экономических вопросов, которые не могут быть адресованы к временным рядам и пространственным рядам в отдельности;

3) они позволяют предотвратить смещение агрегированности, неизбежно возникающее как при анализе временных рядов (где рассматривается временная эволюция усредненного «репрезентативного» объекта), так и при анализе пространственных рядов (где не учитываются ненаблюдаемые индивидуальные характеристики объектов);

4) они дают возможность проследить индивидуальную эволюцию характеристик объектов во времени.

5) они дают возможность избежать ошибок спецификации, возникающих от невключения в модель существенных переменных.

Существующие проблемы панельных исследований:

смещение в данных (отсутствие или искажение ответов на отдельные вопросы)

истощение выборки (постепенное убывание числа объектов наблюдения: отказ участвовать в опросах в дальнейшем, распад домохозяйств) и ротационные панели как решение проблемы истощения.

Решить данные проблемы помогают специальные техники between и within, которые будут рассмотрены далее более подробно.

Модели панельных данных широко используются в микро- и макроэкономических исследованиях, например:

2. Объекты – коммерческие фирмы; переменные – оборот, прибыль, число сотрудников, отрасль; результирующий показатель – рыночная стоимость.

3. Объекты – регионы; параметры – уровень жизни, среда и ресурсы, демография и миграции, политика, экономика и социальная сфера, культура, образование, внешние условия; результирующий показатель – индекс конфликтов.

Регрессионные модели панельных данных:

1. Общая регрессионная модель (pooled least squares)

2. Модель с детерминированными эффектами (fixed effects model)

3. Модель со случайными эффектами (random effects model)

Общая регрессионная модель (pooledleastsquares)

Регрессионная модель панельных данных отличается от регрессии обычных временных рядов или пространственной регрессии тем, что её переменные имеют двойной нижний индекс, т.е.

Большинство приложений панельных данных использует однокомпонентную модель случайной ошибки ν_i,t:

Модель с детерминированными эффектами (fixed effects model)

При построении моделей анализа панельных данных потребность учитывать индивидуальные особенности объектов приводит к следующей проблеме: наиболее эффективные методы оценивания оказываются несостоятельными, а состоятельные методы дают неэффективные оценки коэффициентов регрессионных соотношений. В частности, переход к центрированным по времени наблюдениям – техника “Within” – позволяет избавиться от индивидуальных эффектов, но в то же время, приводит к существенной потере эффективности. Рассмотрение тех же регрессионных соотношений для средних по времени значений переменных (“Between” ) позволяет оценить величину вклада индивидуальных эффектов в изменчивость зависимых переменных, но эти оценки имеют сильное смещение агрегированности.

Модель со случайными эффектами (random effects model)

В модели с фиксированными эффектами слишком много параметров и потери степеней свободы можно избежать, если предположить индивидуальные эффекты μ_iслучайными. Тогда можно предполагать, что u_i

IID(0, σ_ε 2 ), и μ_i не зависят от ε_it. Кроме того, X_itне зависят от u_i и ε_it для всех i и t. Модель со случайными эффектами применяется в том случае, если мы выбираем случайным образом Nобъектов из большой генеральной совокупности элементов, например, в случае исследований панелей домашних хозяйств, индивидуумов или мелких фирм. Другим примером могут служить представители однородных товарных групп, образованных товарами-заменителями.

Модель со случайными эффектами можно рассматривать как компромисс между сквозной регрессией, налагающей сильное ограничение гомогенности на все коэффициенты уравнения регрессии для любых i и t, и регрессией FE, которая позволяет для каждого объекта выборки ввести свою константу и, таким образом, учесть существующую в реальности, но ненаблюдаемую гетерогенность.

Поиски такого компромисса бывают вызваны следующими причинами:

• оценки модели FE хотя и состоятельны для статических моделей в отсутствии эндогенности, но часто не очень эффективны. Иными словами, может получиться так, что коэффициенты при наиболее интересующих нас переменных окажутся незначимы;

• модель FE не позволяет оценивать коэффициенты при инвариантных по времени регрессорах, так как они элиминируются из модели после преобразования «within».

Сквозная регрессионная модель хотя и лишена этих недостатков, но часто дает несостоятельные оценки, поскольку никак не учитывает индивидуальную гетерогенность.

В модели со случайными эффектами (u_i – случайны) индивидуальная гетерогенность учитывается не в самом уравнении, а в матрице ковариаций, которая имеет блочно-диагональный вид, так как внутри каждой группы случайные эффекты корреллируют между собой. Для оценивания такой регрессии следует использовать обобщенный метод наименьших квадратов (GLS).

1. Тест Хаусмана — применяемый эконометрике тест для сравнения моделей, оцененных разными методами, один из которых позволяет получить состоятельные оценки (факторы модели являются экзогенными) и при нулевой и при альтернативной гипотезе, а другой — только при нулевой гипотезе. Если статистика теста превышает критическое значение, регрессоры модели нельзя считать экзогенными, поэтому лучше использовать метод инструментальных переменных. В противном случае можно считать, что регрессоры не хуже инструментов и применять обычный МНК.

Таким образом, последовательно рассмотрев основные преимущества и проблемы панельных данных, основные регрессионные модели и практический пример использования панельных данных, цель работы была достигнута. На практическом примере были разобраны регрессионная модель со случайными эффектами и модель с фиксированными переменными. Следует отметить, что панельные данные могут быть использованы как для анализа экономических взаимосвязей, так и социально-экономических, как например взаимосвязь содержания диоксида углерода в воздухе с ВВП.

Источник

Временные ряды и данные поперечного сечения можно рассматривать как особые случаи панельных данных, которые находятся только в одном измерении (один член панели или отдельное лицо для первого, одна временная точка для последнего).

Исследование, в котором используются панельные данные, называется лонгитюдным исследованием или панельным исследованием.

СОДЕРЖАНИЕ

Пример

Сбалансированная панель MRPP

человек	год	доход	возраст	секс
1	2016 г.	1300	27	1
1	2017 г.	1600	28 год	1
1	2018 г.	2000 г.	29	1
2	2016 г.	2000 г.	38	2
2	2017 г.	2300	39	2
2	2018 г.	2400	40	2

Несбалансированная панель MRPP

человек	год	доход	возраст	секс
1	2016 г.	1600	23	1
1	2017 г.	1500	24	1
2	2016 г.	1900 г.	41 год	2
2	2017 г.	2000 г.	42	2
2	2018 г.	2100	43 год	2
3	2017 г.	3300	34	1

В приведенном выше примере процедуры перестановки множественных ответов ( MRPP ) показаны два набора данных с панельной структурой, и цель состоит в том, чтобы проверить, есть ли значительная разница между людьми в выборке данных. Индивидуальные характеристики (доход, возраст, пол) собираются для разных людей и разных лет. В первом наборе данных два человека (1, 2) наблюдаются каждый год в течение трех лет (2016, 2017, 2018). Во втором наборе данных три человека (1, 2, 3) наблюдаются два раза (человек 1), три раза (человек 2) и один раз (человек 3), соответственно, в течение трех лет (2016, 2017, 2018). ; в частности, лицо 1 не наблюдается в 2018 году, а лицо 3 не наблюдается в 2016 или 2018 году.

Анализ

Рассмотрим типичную модель панельных данных:

Данные динамической панели

Данные динамической панели описывают случай, когда в качестве регрессора используется запаздывание зависимой переменной:

Источник

Что такое панельные данные

Сельское хозяйство – крупная отрасль экономики Российской Федерации. Объем производства продукции сельского хозяйства в 2018 г. составил 5,1 трлн руб. При этом на растениеводство приходится 54 %, на животноводство – 46 % объема сельскохозяйственного производства. Россия – крупный экспортер сельскохозяйственной продукции. Ключевая статья экспорта сельскохозяйственного сырья и продовольствия из России в 2018 г. – зерно, что составило 42 % от общих поставок [1].

Показатели сельского хозяйства регионов РФ представляют собой панельные данные. Существенное различие между панельными и пространственными данными состоит в том, что в первом случае у нас имеются наблюдения за однотипными объектами во все периоды времени. Данные, представляемые в виде временных рядов, представляют собой наблюдения за одним объектом, но за некоторый промежуток времени. Следовательно, такие данные позволяют учитывать фактор времени.

Панельные данные представляют собой объединение пространственных данных и временных рядов.

Целью настоящего исследования являются выявление, анализ влияния объемов производства сельскохозяйственной продукции на валовой региональный продукт (ВРП) и его прогнозирование с помощью моделей панельных данных.

Материалы и методы исследования

Объектом настоящего исследования являются регионы РФ. Исходные данные исследования – показатель валового регионального продукта и «Продукция сельского хозяйства» в разрезе регионов РФ (федеральных округов (ФО)) и в целом за 2010–2017 гг.

Панель сбалансирована по выбранным показателям и по периоду исследования (а именно удалены наблюдения, по которым нет полных данных). В том числе не взяты данные показателя «Продукция сельского хозяйства» за 2018 г., поскольку в [1] отсутствуют данные ВРП за аналогичный год.

В результате исходные данные за 2010–2017 гг. составляют в общем по стране данные 81 региона (648 наблюдений), в том числе ЦФО – 17 регионов (136 наблюдений); СЗФО – 10 регионов (80 наблюдений); ЮФО – 6 регионов (48 наблюдений); СКФО – 7 регионов (56 наблюдений); ПФО – 14 регионов (112 наблюдений); УрФО – 6 регионов (48 наблюдений); СФО – 12 регионов (96 наблюдений); ДФО – 9 регионов (72 наблюдения).

По представленным данным составляются три вида моделей панельных данных: объединенная, с фиксированными и случайными эффектами.

Объединенная (pooled) модель имеет вид:

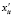
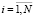
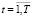
где y_it – результативный показатель, – показатель-фактор, µ и β – параметры модели, uit – ненаблюдаемые остатки, – номер объекта, – момент времени.

Модель с фиксированными эффектами (fixed effects model) имеет вид:

В модели с фиксированными эффектами параметр β одинаков для всех объектов наблюдения во все моменты времени, а параметр местоположения µ_i индивидуален для каждого объекта наблюдения.

Модель со случайными эффектами имеет вид:

где .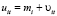

В этой модели также параметр β одинаков для всех объектов наблюдения, а специфичным для них является слагаемое mi, которое предполагается независимым от оставшейся части ошибки υ_it.

Модель называют «со случайными эффектами», так как эффекты mi, определяющие разнородность объектов, являются случайными переменными. Однако это не означает, что mi определяются для каждого наблюдения в случайном порядке. Здесь имеет место случайность выборки из генеральной совокупности, так как любой объект наблюдения имеет специфический эффект, который не зависит от времени.

Вопрос о спецификации моделей, т.е. о том, какую из двух последних моделей выбрать в настоящем исследовании, решается с помощью теста Хаусмана. При проведении теста Хаусмана выдвигаются две гипотезы: Н0 – оценки обеих моделей состоятельны и не отличаются слишком сильно; Н1 – оценки для модели с фиксированными эффектами являются состоятельными, а для модели со случайными эффектами – уже нет.

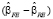
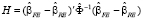
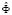
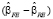
Тест Хаусмана основан на разности : , где – оценка матрицы ковариаций , имеющая асимптотическое распределение χ2 с d степенями свободы [2, 3].

Результаты исследования и их обсуждение

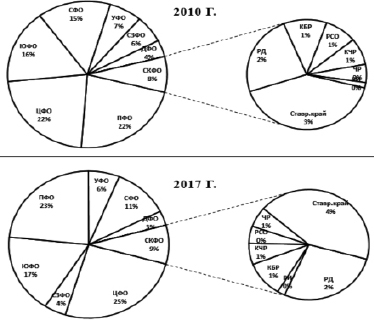
На рис. 1 представлены диаграммы, отражающие структуру показателя «Продукция сельского хозяйства» в разрезе федеральных округов РФ и в разрезе регионов СКФО в 2010 и 2017 гг.

Согласно рис. 1 крупными производителями продукции сельского хозяйства в России являются регионы Центрального, Приволжского и Южного федеральных округов. Причем такое распределение имеет место как в 2010 г., так и в 2017 г. При этом на долю этих регионов приходится 60 % и 65 % от общего объема в 2010 и 2017 гг. соответственно.

Регионы СКФО занимают в рассматриваемые периоды 5-е место. При этом Ставропольский край производит 41 % и 43 %, Республика Дагестан – 24 % и 27 %, Карачаево-Черкесская Республика – 12 % и 11 % от общего объема продукции сельского хозяйства СКФО соответственно в 2010 и 2017 гг.

На рис. 1 вторичная диаграмма отражает структуру показателя «Продукция сельского хозяйства» в разрезе регионов СКФО со значениями в процентах от общего объема этого показателя по стране в целом.

На рис. 2 представлены временные ряды ВРП и показателя «Продукция сельского хозяйства» регионов РФ за 2010–2017 гг.

Значительно высокие значения показателя «Продукция сельского хозяйства» за рассматриваемый период принадлежат Краснодарскому краю.

Рис. 1. Структура показателя «Продукция сельского хозяйства» федеральных округов РФ (первичная диаграмма) и в разрезе регионов СКФО (вторичная) в 2010 и 2017 гг.

Рис. 2. Временные ряды ВРП и показателя «Продукция сельского хозяйства» регионов РФ за 2010–2017 гг.

В табл. 1 представлены некоторые результаты оценивания моделей панельных данных, полученные с помощью пакета для эконометрического анализа «Eviews».

Индекс детерминации для модели с фиксированными эффектами высокий и составляет 0,95, для остальных моделей он незначительный – 0,12 и 0,24 (для модели со случайными эффектами см. в табл. 1). Критерий Стьюдента для всех моделей больше табличных значений, что свидетельствует о статистической значимости параметров моделей.

Математическая запись моделей приводится в табл. 2.

Параметры и статистические характеристики модели со случайными эффектами, построенной по сбалансированным наблюдениям за 81 регионом РФ в 2010–2017 гг., полученные с помощью пакета «Eviews»

Источник