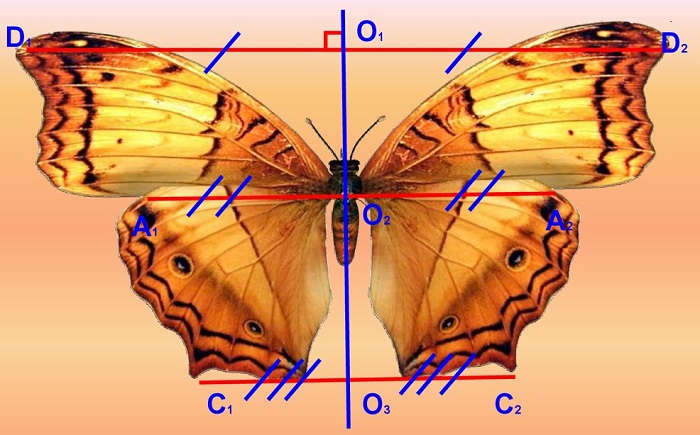
что такое ось симметрии 3 класс правило

Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.

Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.

Что такое симметрия

Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.

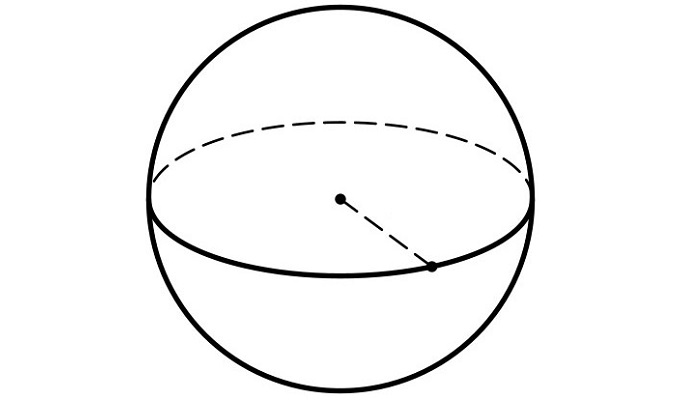
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.

Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.

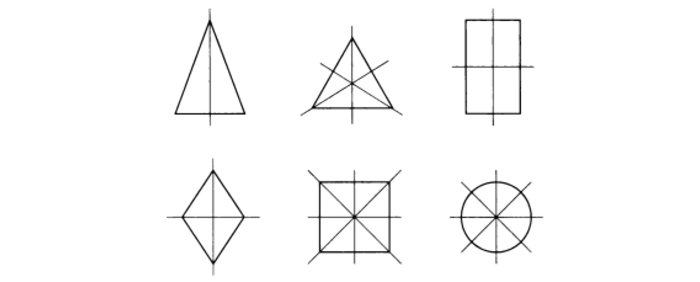
Рис. 1 Фигуры, обладающие симметричностью

Центральная симметрия

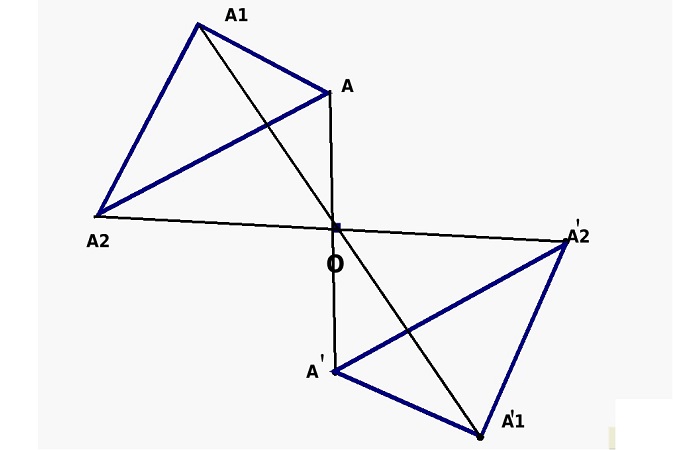
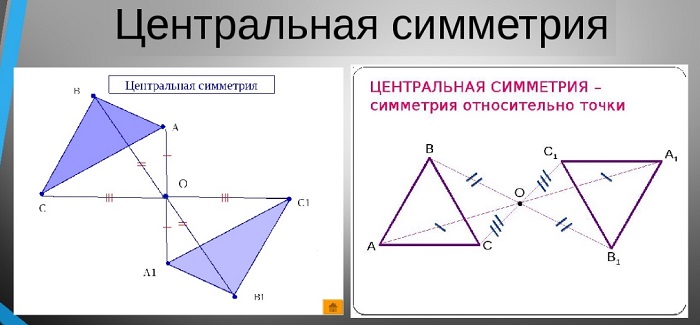
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.

Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.

Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

Рис. 2 Графическое представление центральной симметрии

Осевая симметрия

Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.

Рис. 3 Наглядное представление осевой симметрии

В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.

Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.

Рис. 4 Примеры осевой симметрии

Фигуры, имеющие несколько осей симметрии

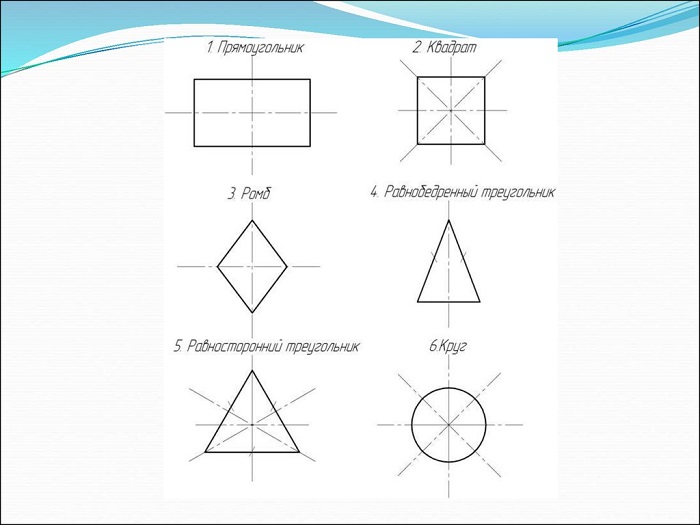
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.

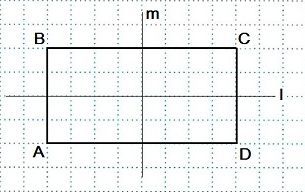
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.

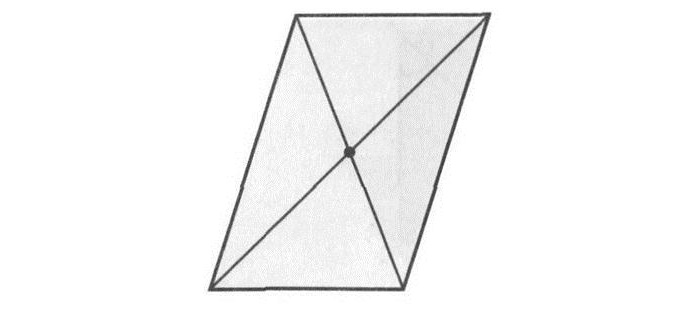
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.

Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.

Рис. 5 Оси симметрии ромба

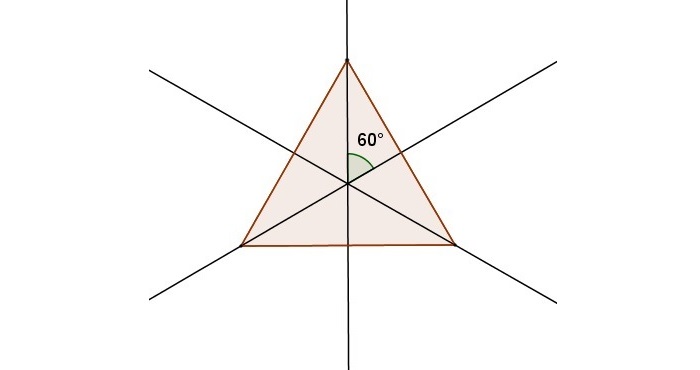
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.

Рис. 6 Оси симметрии равностороннего треугольника

В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.

Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.

Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.

Источник

Урок математики в 3-м классе по теме «Симметричные фигуры»

Ход урока

1. Организационный момент.

Учиться надо весело, учиться надо дружно,
Чтобы на математике нам не было бы скучно.

2. Запись числа. Чистописание.

— Какую закономерность вы заметили в записи чисел?

/В тетрадях показ учителя: 913, 823, 733./

Дети отвечают: “В каждом последующем числе сотни уменьшаются на 1 единицу, десятки увеличиваются на 1 единицу, а единицы не меняются”.

3. Объявление темы урока.

— Сегодня на уроке мы продолжим разговор о симметрии. Прочитайте название темы. /На доске запись: “Симметричные фигуры. Ось симметрии”./
— Поставьте себе цель, что бы вы хотели узнать на уроке.

/Дети отвечают, что хотели бы узнать, что такое ось симметрии, что-нибудь новое о симметрии и т. п./

4. Устный счёт.

— Начнём с подготовки, как спортсмены. Чтобы преодолеть трудности, нужно хорошо тренироваться.

В двух бочках 30 литров мёда, при чём, в первой на 4 литра мёда больше. Сколько литров мёда во второй бочке?

Ответ: (30 – 4) : 2 = 13(л)

б) 1 ученик работает за компьютером.

— Какие точки являются симметричными?
— Выдели их цветом. Объясни, почему так думаешь?

в) Во время индивидуальной работы учащихся весь класс работает с учителем фронтально по записи на доске.

60705 + 124 124 + 60705
64 • 308 308 • 64
756 • 32 28 • 756
3094 – 86 3094 – 806
2089 – 916 3000 – 916
10735 : 113 10735 : 5

— Сравните выражения, не вычисляя. Обоснуйте свой ответ.

(Дети объясняют постановку знака, используя знания предыдущих тем.)

Проверка индивидуальной работы. Выставление оценок.

5. Новая тема.

— Отправляемся в поход за новыми знаниями на гору Знаний.

(Дети выставляют сигналы со своей фотографией на ту ступень, которая соответствует их знаниям по данной теме. Так делается всегда при изучении новой темы. Затем по мере изучения темы, они передвигают сигнал с низкой ступени на более высокую ступень. Когда ребёнок посчитает, что он тему понял, сигнал оказывается на вершине. Так дети учатся определять уровень своих знаний с помощью игры.)

— Выставьте свои сигналы. (Рисунок №1)
— Рассмотрите на доске рисунки. Как они связаны с темой нашего урока? (На доске рисунки: №2, №3, №4. Ученики рассматривают их и высказывают свои предположения.)
— Мне нужен помощник (Приглашается 1 ученик.).
— Сложи модель бабочки по вертикали. Что заметил? (Ребёнок говорит, что части совпали.)

— Назовём линию сгиба модели прямой l. Модель бабочки теперь состоит из двух половин, симметричных друг другу относительно прямой l. Прямая l на модели является осью симметрии (прикрепляю к доске слова на карточке).

Вывод: изображение бабочки симметрично относительно прямой l, а прямая l – её ось симметрии.

— Что можете сказать об остальных моделях?

(Дети рассуждают, доказывают.)

— Итак, как вы поняли, что значит, фигура симметрична относительно прямой l? (Учащиеся делают вывод.)

б) Работа с правилом.

— Прочитайте правило на стр. 46.
— Работаем в паре. Заучиваем и рассказываем правило соседу по парте.
— Приведите примеры симметричных фигур в классе.
— Посмотрите на гору Знаний. Передвиньте свой сигнал, если ваши знания по теме изменились.

— Найдите задание №1, стр. 46. Прочитайте.
— Почему буква Н имеет две оси симметрии?
— Назовите другие буквы, имеющие ось симметрии.

6. Физминутка.

Поднимайте плечики,
Прыгайте, кузнечики,
Прыг-скок, прыг-скок.
Сели, травушку покушаем,
Тишину послушаем.
Тише, тише, высоко,
Прыгай на носках легко.

7. Практическая работа.

Каждый ученик берёт карточку с практической работой, на которой нужно дорисовать симметричные фигуры и самостоятельно выполняет задание.

Взаимопроверка работ учащимися.

б) Индивидуальная работа за компьютером. Выполняет 1 ученик.

— Отметь симметричные фигуры.

(Дети делают вывод, опираясь на выполненную работу.)

— Переместите свой сигнал на горе Знаний, если ваши знания изменились.

8. Повторение.

№8, стр.47 – самостоятельная работа.

— Внесите данные в чертёж и решите задачу с пояснением.

1) 18 • 2 = 36 (руб.) – стоимость конфет;
2) 12 • 3 = 36 (руб.) – стоимость печенья;
3) 90 – (36 + 36) = 18 (руб.) – стоимость 3 булочек;
4) 18 : 3 = 6 (руб.) – стоимость 1 булочки.

№5, стр. 47 – работа в парах.

— Повторим деление и умножение круглых чисел. Первый ряд решает примеры 1 столбика, а 2 и 3 ряды – примеры 2 столбика.

9. Итог урока.

— Подведём итог урока.
— На ваших партах лежат модели фигур. Возьмите любую фигуру. С помощью перегибания найдите её ось симметрии.

— Что можно сказать о фигуре после сгибания? (Она симметрична относительно оси l.)
— Посмотрите, какая ступень горы Знаний вами преодолена последней.

Источник

Презентация к уроку «Ось симметрии фигуры» 3 класс

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Платон. Годы жизни 429-327 до н.э.

1. Перегнуть пополам. 2. Зафиксировать линию сгиба. 3. Развернуть фигуру. 4. Провести прямую линию.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Презентация к конспекту урока по теме «Ось симметрии фигуры». Урок второй в разделе Ось симметрии фигуры.

Презентация предназначена для повторения пройденного материала и правила нахождения оси симметрии практическим путём, упражнения в построении оси симметрии и сличения работы, выполненной на уроке с образцом.

Номер материала: ДБ-938077

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

На Госуслугах ввели запись детей на кружки и секции

Время чтения: 2 минуты

В Москве запустили онлайн-проект по борьбе со школьным буллингом

Время чтения: 2 минуты

С 2019 года закрыто более 50 детских лагерей

Время чтения: 1 минута

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

В Ульяновской области продлили школьные каникулы

Время чтения: 1 минута

СК предложил обучать педагогов выявлять деструктивное поведение учащихся

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Осевая симметрия — виды, свойства и примеры фигур

Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.

Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.

Что такое симметрия

Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.

В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.

Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.

Рис. 1 Фигуры, обладающие симметричностью

Центральная симметрия

Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.

Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.

Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

Рис. 2 Графическое представление центральной симметрии

Осевая симметрия

Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.

Рис. 3 Наглядное представление осевой симметрии

Объект симметричен относительно прямой, если все его точки имеют такие же симметричные аналоги относительно этой прямой. Она же — центр симметрии.

В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.

Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.

Рис. 4 Примеры осевой симметрии

Фигуры, имеющие несколько осей симметрии

Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.

Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.

То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.

Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.

Рис. 5 Оси симметрии ромба

Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.

Рис. 6 Оси симметрии равностороннего треугольника

В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.

Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.

Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.

Источник

Конспект урока по теме «Ось симметрии фигуры» 3 класс

Ищем педагогов в команду «Инфоурок»

Тема: Ось симметрии фигуры (2 урок)

Цель: упражнение в построении оси симметрии.

Задачи: 1. Создание условий для трансформации теоретических знаний в практические умения.

2. Формирование навыков самоконтроля, как способа действий через практическую проверку правильности проведения оси симметрии.

3. Обобщение представлений о геометрических фигурах через упражнение построения оси симметрии.

4. Формирование умения действия по алгоритму.

Материально-техническое оснащение: учебник С.С. Минаева, Л.О. Рослова, О.А.Рыдзе (2 часть), компьютер, проектор, презентация к уроку, канцтовары для практической работы (листы в клеточку, ножницы, линейка, карандаш), раздаточный материал (геометрические фигуры), наглядный материал (геометрические фигуры).

-Здравствуйте! Садитесь. Меня зовут Виктория Анатольевна. Сегодня я проведу у вас урок математики.

-Скажите, что на доске?

-Какое у них общее название?

-Откройте учебник на странице 90. В каком математическом разделе вы работали на прошлом уроке?

— Что нового вы узнали?

-Что такое ось симметрии?

-Замечательно. Осевая симметрия присуща всем формам в природе и является одним из основополагающих принципов красоты. Впервые обосновали понятие симметрии не только математики, а еще художники и философы Древней Греции. Древнегреческий философ Платон, живший в 429-327 годах до нашей эры, утверждал, что прекрасным может быть тот объект, который симметричен и соразмерен.

-На прошлом уроке вы познакомились с алгоритмом нахождения оси симметрии. Давайте его повторим.

— А теперь встанем и все вместе повторим алгоритм.

— Хорошо. Давайте выполним упражнение 254 на странице 92. Прочитайте задание.

Упражнение выполнять будем устно.

-Замечательно. Давайте выполним упражнения 252. Прочитайте задание.

-Выполните упражнение самостоятельно в тетради. На выполнение задания 3 минуты.

-Как вы проводили ось симметрии

Значит для того, чтобы провести ось симметрии у окружности, нужно провести ее через центральную точку.

Посмотрите у соседа по парте, там же у него проведена ось симметрии?

Но и у вас и у соседа тоже ось симметрии окружности, не смотря на то, что она в разных местах?

Какой вывод можно сделать? Сколько осей симметрии у окружности?

-Хорошо. Поработаем над упражнением 255. Прочитайте задание.

-Выполнять будем по рядам самостоятельно в тетради. 1 ряд – а); 2 ряд – б); 3 ряд – в). На выполнение задание 3 минуты.

-Напомните мне, что такое радиус?

-Чему равен радиус нашей окружности?

А что такое диаметр?

-Чему равен диаметр окружности?

-Какой из этих отрезков (радиус или диаметр) можно назвать осью симметрии? Почему?

-Мы с вами узнали, что у окружности бесконечное множество осей. Данный вывод можно отнести к другим фигурам?

Каждый ряд будет выполнять поиск осей симметрии у своей фигуры.

У вас на столе лежат конверты. В них листочки в клетку. Возьмите их и выполните на них задание. Фигуру надо нарисовать и вырезать. С помощью алгоритма выполнить поиск всех возможных осей симметрии.

Перед выполнением задания давайте вспомним правила безопасности при работе с ножницами.

Замечательно. Приступайте к работе.

1 ряд: сколько осей симметрии у вашей фигуры получилось?

У всех получилась одна?

2ряд: сколько осей симметрии у прямоугольника?

У всех получилась две?

3ряд: сколько осей симметрии получилось у квадрата. Какие это оси?

Диагональ является осью симметрии?

-Сегодня мы с вами практическим путем узнали, что диагональ является осью симметрии.

-Как вы думаете, у всех ли треугольников одна ось симметрии?

У вас на столе лежит треугольник. Возьмите его и измерьте его стороны? Что вы заметили?

Это равносторонний треугольник. Давайте узнаем сколько у него осей симметрии.

Сколько осей симметрии вы нашли?

Треугольник оказывается сложная фигура. Есть еще много разных видов треугольников. Дома, если хотите, пробуйте найти их оси симметрии.

— А сейчас, давайте все вместе поработаем над упражнением 259. Прочитайте условие под буквой а).

Устно выполним задание.

Под буквой б) выполните дома.

-Замечательно. Давайте вспомним сколько осей симметрии у каждой фигуры мы сегодня нашли?

-Хорошо, а какой геометрической фигурой является поверхность парты?

-Сколько и какие оси симметрии у прямоугольника?

Дети, желаю вам никогда не проводить ось симметрии на парте, как разделительную полосу между соседом.

-В завершении сегодняшнего урока, прошу вас на листочках, которые лежат на вашем столе, закончить фразы. Подписывать листочки не нужно. После звонка сдайте их мне.

— Ось симметрии фигуры

— Что такое ось симметрии

Как построить ось симметрии

— Ось симметрии – это прямая линия, разделяющая фигуру на две равные части.

1.Перегнуть фигуру пополам.

2.Путем прижима зафиксировать линию сгиба.

3. Развернуть фигуру.

4. Провести прямую линию.

Дети встают и повторяют.

Ученик читает задание к упражнению.

Дети отвечают, ответ проверяется на слайдах.

Ученик встает и доказывает, является ли линия ОК осью симметрии.

Ученик читает задание к упражнению.

Дети выполняют задание.

Дети отвечают (через центральную точку)

— У окружности бесконечное множество осей симметрии

Ученик читает задание к упражнению.

Дети выполняют задание.

-Радиус — отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.

Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.

Диаметр, потому что диаметр делит круг на две равные симметричные части.

Дети практическим путем ищут оси симметрии у треугольника.

-Вертикальная и горизонтальная

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Конспект урока по теме «Ось симметрии фигуры». Второй урок в данной теме. Цель урока: упражнение в построении оси симметрии фигуры. К уроку потребуется:

учебник С.С. Минаева, Л.О. Рослова, О.А.Рыдзе(2 часть), компьютер, проектор, презентация к уроку, канцтовары для практической работы (листы в клеточку, ножницы, линейка, карандаш), раздаточный материал (геометрические фигуры), наглядный материал (геометрические фигуры).

Номер материала: ДБ-938065

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В Москве запустили онлайн-проект по борьбе со школьным буллингом

Время чтения: 2 минуты

СК предложил обучать педагогов выявлять деструктивное поведение учащихся

Время чтения: 1 минута

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

Минобрнауки разработало концепцию преподавания истории российского казачества

Время чтения: 1 минута

Вузам Москвы и Подмосковья рекомендовали с 8 ноября ввести смешанный формат обучения

Время чтения: 1 минута

Технопарк универсальных педагогических компетенций откроют в Чечне

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник