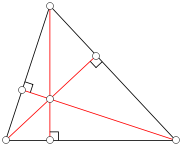
что такое ортоцентр треугольника

Ортоцентр

Ортоцентр (от греч. ορθοξ — прямой) — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).

Содержание

Свойства

История

См. также

Литература

Ссылки

Полезное

Смотреть что такое «Ортоцентр» в других словарях:

ортоцентр — ортоцентр … Орфографический словарь-справочник

ОРТОЦЕНТР — (от греч. orthos прямой правильный и центр), точка пересечения трех высот треугольника … Большой Энциклопедический словарь

ОРТОЦЕНТР — ОРТОЦЕНТР, ортоцентра, муж. (от греч. orthos правильный и лат. centrum центр) (мат.). Точка пересечения трех высот треугольника. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

ортоцентр — сущ., кол во синонимов: 1 • точка (100) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Ортоцентр — (от греч. orthós прямой, правильный и лат. centrum центр) точка пересечения трёх высот треугольника (см. рис.). Во всяком треугольнике точка пересечения медиан, центр описанного круга и О. лежат на одной прямой. Рис. к ст … Большая советская энциклопедия

ортоцентр — (от греч. orthós прямой, правильный и центр), точка пересечения трёх высот треугольника. * * * ОРТОЦЕНТР ОРТОЦЕНТР (от греч. orthos прямой, правильный и центр (см. ЦЕНТР (в математике))), точка пересечения трех высот треугольника … Энциклопедический словарь

ортоцентр — ортоцентр, ортоцентры, ортоцентра, ортоцентров, ортоцентру, ортоцентрам, ортоцентр, ортоцентры, ортоцентром, ортоцентрами, ортоцентре, ортоцентрах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов

ОРТОЦЕНТР — треугольника точка пересечения трех высот треугольника. О. треугольника лежит на Эйлера прямой. Середины трех сторон, середины отрезков, соединяющих О. с тремя вершинами, и основания высот треугольника лежат на одной окружности. О. является… … Математическая энциклопедия

ОРТОЦЕНТР — (от греч. orthоs прямой, правильный и центр), точка пересечения трёх высот треугольника … Естествознание. Энциклопедический словарь

Источник

Точка пересечения высот треугольника — свойства, координаты и расположение ортоцентра

Точка пересечения высот треугольника называется ортоцентром и традиционно обозначается латинской буквой H. «Ортос» в переводе с греческого означает «прямой», «правильный». Ортоцентр может находиться внутри фигуры и вне ее. Местоположение зависит только от самой фигуры и не зависит от порядка расположения сторон и вершин.

Что такое высота

Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.

У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.

Свойства ортоцентра

Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.

Ортоцентр по отношению к фигуре может быть расположен:

Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.

Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:

Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.

Полезные факты

Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.

Пусть:

Тогда:

Задача Фаньяно

Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.

Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.

Площадь ортотреугольника рассчитывается по формуле:

Здесь S — площадь, а, b, c — стороны.

Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.

История изучения

Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.

В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.

Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.

Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.

Источник

Ортоцентр треугольника. Ортотреугольник. Свойства ортоцентра треугольника

Ортоцентр — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).

Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек.

Радиусы окружностей проходящих через любые три точки ортоцентрической системы равны.

Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).

Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.

Точки, симметричные ортоцентру относительно его сторон, лежат на описанной окружности.

Точки, симметричные ортоцентру относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.

Если О — центр описанной окружности ΔABC, то .

Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.

Ортотреуго́льник (ортоцентрический треугольник) треугольника ∆ABC — треугольник, вершины которого являются основаниями высот ∆ABC.

Свойства

2. Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (следовательно ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).

3. Если точки A₁, B₁ и C₁ на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что

, и ,

4. Точки касания вписанной в данный треугольник окружности соединены отрезками, и в полученном треугольнике проведены высоты. Тогда прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника.

7. Высоты треугольника являются биссектрисами ортотреугольника.

9. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.

Дата добавления: 2018-05-13 ; просмотров: 2441 ; Мы поможем в написании вашей работы!

Источник

Научно-исследовательская работа по математике «Ортоцентрический треугольник»

Ищем педагогов в команду «Инфоурок»

Тема: Свойства ортоцентрических треугольников

Руководитель Т.Н. Морозова,

Учащийся А.Р. Метшина

Глава 1. Исторические сведения и свойства 4

§ 2. Исторические сведения 4

§ 3. Свойства ортотреугольников 4

Глава 2. Применение 6

§ 1. Применение свойств ортотреугольника для решения задач 6

Список используемой литературы 11

Предметом нашего исследования являются ортоцентрические треугольники и их свойства.

Цель – изучение свойств ортоцентрических треугольников и исследование путей их использования для решения задач.

1) выяснить, что такое ортотреугольник;

2) изучить и проанализировать свойства ортотреугольников;

3) рассмотреть возможное применение

этих свойств для решения задач.

Во время выполнения поставленных задач нами был использован описательный метод исследования, изучение и обобщение.

Практическая значимость: результаты проведенного исследования могут стать опорой для решения олимпиадных задач, задач ЕГЭ и ОГЭ с использованием свойств отроцентрических треугольников.

Глава 1. Исторические сведения и свойства

§ 1. Что такое ортоцентрический треугольник?

Ортотреуго́льник (ортоцентрический треугольник) — это треугольник Δ A ₁ B ₁ C ₁, вершины которого являются основаниями высот треугольника ∆ABC. Для ортотреуго́льника (для ортоцентрического треугольника) Δ A ₁ B ₁ C ₁ сам треугольник ∆ABC является треугольником трёх внешних биссектрис. То есть отрезки AB, BC и CA являются тремя внешними биссектрисами треугольника Δ A ₁ B ₁ C ₁.

§ 2. Исторические сведения

§ 3. Свойства ортотреугольников

1.Теорема о подобии треугольников. Ортотреугольник отсекает треугольники, подобные данному.

Как следствие данной теоремы, верно следующее утверждение:

Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.

Среди всех треугольников, вписанных в данный треугольник, только ортотреугольник обладает указанным свойством.

І. Ортоцентрический треугольник H₁H₂H₃ В остроугольном треугольнике ABC соединим отрезками основания высот H₁, H₂, H₃ (рис. 1). Получим

треугольник H₁H₂H₃. Рассмотрим некоторые свойства этого треугольника, которые используют при решении задач.

Свойство 1. Стороны ортоцентрического треугольника H₁H₂H₃ антипараллельны сторонам треугольника ABC.

Доказательство. Обозначим точку H — точку пересечения высот треугольника ABC (ортоцентр). Опишем окружность около четырёхугольника AH₂HH₃. Тогда ∠ AH₂H₃ = ∠ AHH₃ = ∠ ABC, значит, сторона H₂H₃ антипараллельна стороне BC. Аналогично доказывается антипараллельность двух других сторон треугольника

Свойство 2. Высоты треугольника ABC являются биссектрисами внутренних углов треугольника H₁H₂H₃.

Свойство 3. Отрезок OA перпендикулярен отрезку H₂H₃.

Доказательство. Действительно, если описать окружность около треугольника H₁H₂H₃, дуги, на которые опираются углы ∠ H₂H₁A и ∠ AH₁H₃, равны, а значит, OA ⊥ H₂H₃ (рис. 2).

Свойство 4. Вершины треугольника ABC являются центрами вневписанных окружностей ортоцентрического треугольника H₁H₂H₃ (рис. 3).

Свойство 5. Имеет место формула p_H = h_asinA, где p_H — полупериметр треугольника H₁H₂H₃, h_a — высота AH₁.

Свойство 6. Имеет место формула S = Rp_H, где S — площадь треугольника ABC, R — радиус окружности, описанной около треугольника ABC.

Доказательство. Действительно, поскольку p_H = h_asinA, то

Свойство 7. Окружность Леонарда Эйлера.

Доказательство. Опишем окружность около треугольника H₁H₂H₃. Докажем, что окружности (обозначим её γ _e ), кроме точек H₁, H₂, H₃, принадлежат середины отрезков AH, BH, CH (их называют точками Эйлера и обозначают E₁, E₂, E₃), ещё три точки M₁, M₂, M₃ — середины сторон BC, AC, AB. Начнём с точек Эйлера. Заметим, что доказательство нестандартно (рис. 4).

около треугольника H₁H₂H₃, будет серединой дуги H₂H₃, то есть точкой W₁ треугольника H₁H₂H₃, а точка A — центром вневписанной

окружности (свойство 4).

Воспользуемся свойством вневписанных окружностей с центрами I_b и I_c. Пусть W₁ A — точка, диаметрально противоположная точке W₁. Тогда W₁ A — середина отрезка I_bI_c. Пусть окружность γ _e пересекает сторону BC в точке X (рис. 4). Поскольку ∠ E₁H₁X₁ = 90°, то точки X и E₁ диаметрально противоположны, а поскольку точка E₁ есть точкой W₁ окружности, то точка X совпадает с серединой отрезка BC (точки B и C — центры вневписанных окружностей). Теорема об окружности Эйлера для треугольника ABC доказана новым способом.

ІІ. Ортоудвоенный треугольник

Высоты AH₁, BH₂, CH₃ продолжим до пересечения с описанной окружностью (рис. 5).

Получим треугольник N ₁N₂N₃, который назовём ортоудвоенным. Поскольку HH₁ = H₁N₁, HH₂ = H₂N₂, HH₃ = H₃N₃, то этот треугольник гомотетичен треугольнику H₁H₂H₃ с центром гомотетии — серединой отрезка OE ( E — центр окружности Эйлера) и коэффициентом гомотетии k =

Свойство 2. Высоты треугольника ABC принадлежат биссектрисам внутренних углов треугольника N ₁N₂N₃.

Доказательство. Действительно, это следует из свойства 1.

Свойство 3. Радиус OA перпендикулярен отрезкам N₂N₃ и H₂H₃.

Доказательство. Действительно, это следует из свойства 1.

Свойство 4. Точка, симметричная ортоцентру H относительно середины M₁ отрезка BC принадлежит окружности, описанной около треугольника

ABC.

Доказательство. Проведём диаметр AA₁ (рис.6) и найдём точку X, гомотетичную точке A₁. Поскольку A₁X = XH, то отрезок OX — средняя линия треугольника

AA₁H. Значит, он параллелен AH и равен

AH, то есть OX = OM₁ и точка X совпадает с точкой M₁ — серединой отрезка BC.

Свойство 5. Прямая Эйлера. Центроид M треугольника ABC принадлежит отрезку OH.

Доказательство. Проведём отрезок AM₁ (рис. 6). Он пересечёт OH в точке Y. Поскольку то M ₁ M : AM = 1 : 2, а значит, точка Y совпадает с точкой M₁.

Окружность девяти точек

ІІІ. Ортоцентрический треугольник Q ₁ Q ₂ Q ₃

Опишем окружность около треугольника ABC и построим точки W ₁, W ₂, W ₃ (середины дуг BC, AC, AB) (рис. 7).

Точку пересечения хорд W ₂ W ₃ и AW₁ обозначим Q₁. Аналогично получим точки Q₁ и Q₃. По теореме «листа трилистника» имеем: IW₁ = W₁C. Поскольку ∪ AW₂ = ∪ W₂C, то

Поскольку окружность, описанная около треугольника Q ₁ Q ₂ Q ₃, есть окружность Эйлера треугольника W ₁ W ₂ W ₃, то девять точек принадлежат одной окружности: середины отрезков W ₁ W ₃, W ₂ W ₃, W ₁ W ₂, IW₁, IW₂, IW₃, IA, IB, IC.

ІV. Ортоцентрический треугольник ABC

Рассмотрим треугольник, вершины которого — центры вневписанных окружностей I_a, I_b, I_c (рис.8).

Ортоцентрическим треугольником этого

треугольника будет треугольник ABC, так как

каждая из его вершин есть пересечение внутренней и внешней биссектрис. Поскольку радиус окружности, описанной около треугольника ABC будет R, то радиус окружности, описанной около треугольника I_aI_bI_c будет 2R, а площадь S_IaIbIc=2R ⋅ p.

Поскольку окружность, описанная около треугольника ABC, является окружностью Эйлера треугольника I_aI_bI_c, то девять точек принадлежат одной окружности: вершины треугольника ABC, точки W₁, W₂, W₃, середины

V. Треугольник, подобный ортоцентрическому треугольнику H₁H₂H₃

Через вершины A, B и C проведём касательные к окружности, описанной около треугольника ABC. Получим треугольник T₁T₂T₃ (рис. 9).

Поскольку OA ⊥ H₂H₃ и OA ⊥ T₁T₂, то T₁T₂||H₂H₃, а треугольник T₁T₂T₃ подобен треугольнику H₂H₃H₁. Заметим, что площадь S_T треугольника T₁T₂T₃ (его называют

тангенциальным) вычисляют по формуле:

Глава 2. Применение.

§ 1 Применение свойств ортотреугольника для решения задач

Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?

Следствием данной задачи будет следующее утверждение: каждая сторона ортотреугольника равна произведению противолежащей стороны на косинус противолежащего угла исходного треугольника.

Треугольник АВС остроугольный, и угол ВАС равен α. На стороне ВС как на диаметре построена полуокружность, пересекающая стороны АВ и АС в точках Р и Q соответственно. Найдите отношение площадей треугольников АВС и APQ .

Источник

Что такое ортоцентр треугольника

Предметом нашего исследования являются ортоцентрические треугольники и их свойства.

Цель – изучение свойств ортоцентрических треугольников и исследование путей их использования для решения задач.

1) выяснить, что такое ортотреугольник;

2) изучить и проанализировать свойства ортотреугольников;

3) рассмотреть возможное применение

этих свойств для решения задач.

Во время выполнения поставленных задач нами был использован описательный метод исследования, изучение и обобщение.

Практическая значимость: результаты проведенного исследования могут стать опорой для решения олимпиадных задач, задач ЕГЭ и ОГЭ с использованием свойств отроцентрических треугольников.

Глава 1. Исторические сведения и свойства

§ 1. Что такое ортоцентрический треугольник?

Ортотреуго́льник (ортоцентрический треугольник) — это треугольник ΔA_1B1C₁, вершины которого являются основаниями высот треугольника ∆ABC. Для ортотреуго́льника (для ортоцентрического треугольника) ΔA_1B1C₁ сам треугольник ∆ABC является треугольником трёх внешних биссектрис. То есть отрезки AB, BC и CA являются тремя внешними биссектрисами треугольника ΔA_1B1C₁.

§ 2. Исторические сведения

В начале 18 века итальянский инженер и математик Фаньяно дей Тоски поставил перед собой такую задачу: вписать в остроугольный треугольник АВС треугольник наименьшего периметра так, чтобы на каждой из сторон данного треугольника лежала одна вершина вписанного. Аналитическое решение этой задачи было опубликовано в 1755 году. Было доказано, что существует единственный треугольник наименьшего периметра KMN, его вершина K – основание высоты CK. Искомым треугольником всегда будет ортотреугольник KMN.

§ 3.Свойства ортотреугольников

1.Теорема о подобии треугольников. Ортотреугольник отсекает треугольники, подобные данному.

Как следствие данной теоремы, верно следующее утверждение:

Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.

Среди всех треугольников, вписанных в данный треугольник, только ортотреугольник обладает указанным свойством.

І. Ортоцентрический треугольник H₁H₂H₃ В остроугольном треугольнике ABC соединим отрезками основания высот H₁,H₂,H₃ (рис. 1). Получим

треугольник H₁H₂H₃. Рассмотрим некоторые свойства этого треугольника, которые используют при решении задач.

Свойство 1. Стороны ортоцентрического треугольника H₁H₂H₃ антипараллельны сторонам треугольника ABC.

Доказательство. Обозначим точку H — точку пересечения высот треугольника ABC (ортоцентр). Опишем окружность около четырёхугольника AH₂HH₃. Тогда ∠AH₂H₃ = ∠AHH₃ = ∠ABC, значит, сторона H₂H₃ антипараллельна стороне BC. Аналогично доказывается антипараллельность двух других сторон треугольника

Свойство 2. Высоты треугольника ABC являются биссектрисами внутренних углов треугольника H₁H₂H₃.

Свойство 3. Отрезок OA перпендикулярен отрезку H₂H₃.

Доказательство. Действительно, если описать окружность около треугольника H₁H₂H₃, дуги, на которые опираются углы ∠H₂H₁A и ∠AH₁H₃, равны, а значит, OA⊥H₂H₃ (рис. 2).

Свойство 4. Вершины треугольника ABC являются центрами вневписанных окружностей ортоцентрического треугольника H₁H₂H₃ (рис. 3).

Свойство 5. Имеет место формула p_H = h_asinA, где p_H — полупериметр треугольника H₁H₂H₃, h_a — высота AH₁.

Доказательство. Из точки A опустим перпендикуляр AF на прямую H₁H₃ (рис.3). Поскольку∠H₁AF = ∠H₃H₁B (углы с взаимно перпендикулярными сторонами), то ∠HAF = ∠A и H₁F = h_asinA (из треугольника H A1 F), или p_H = h_asinA.

Свойство 6. Имеет место формула S = Rp_H, где S — площадь треугольника ABC, R — радиус окружности, описанной около треугольника ABC.

Доказательство. Действительно, поскольку p_H = h_asinA, то

p_H= sinA, и S = Rp_H(a — длина стороны BC).

Свойство 7. Окружность Леонарда Эйлера.

Доказательство. Опишем окружность около треугольника H₁H₂H₃. Докажем, что окружности (обозначим её γ_e), кроме точек H₁, H₂, H₃, принадлежат середины отрезков AH, BH, CH (их называют точками Эйлера и обозначают E₁, E₂, E₃), ещё три точки M₁, M₂, M₃ — середины сторон BC, AC, AB. Начнём с точек Эйлера. Заметим, что доказательство нестандартно (рис. 4).

Поскольку прямая H H1 (рис. 4) принадлежит биссектрисе угла ∠H₂H₁H₃, то точка её пересечения с окружностью γ_e, описанной

около треугольника H₁H₂H₃, будет серединой дуги H₂H₃, то есть точкой W₁ треугольника H₁H₂H₃, а точка A — центром вневписанной

окружности (свойство 4).

По теореме Мансиона ( IW₁ = W₁I_a = W₁B = W₁C): AE₁ = E₁H. Значит, точка совпадает с серединой отрезка IW₁ для треугольника H₁H₂H₃ с точкой E₁. Поскольку точки B и C также центры вневписанных окружностей, то утверждение относительно середин отрезков AH, BH и CH доказано. Докажем, что середины AC, BC и AB (точки M₁, M₂, M₃) принадлежат окружности γ_e.

Воспользуемся свойством вневписанных окружностей с центрами Ib и I_c. Пусть W₁ A — точка, диаметрально противоположная точке W₁. Тогда W₁ A — середина отрезка IbI_c. Пусть окружность γ_e пересекает сторону BC в точке X (рис. 4). Поскольку ∠E₁H₁X₁ = 90°, то точки X и E₁ диаметрально противоположны, а поскольку точка E₁ есть точкой W₁ окружности, то точка X совпадает с серединой отрезка BC (точки B и C — центры вневписанных окружностей). Теорема об окружности Эйлера для треугольника ABC доказана новым способом.

ІІ. Ортоудвоенный треугольник

Высоты AH₁, BH₂, CH₃ продолжим до пересечения с описанной окружностью (рис. 5).

Получим треугольник N_1N2N3, который назовём ортоудвоенным. Поскольку HH₁ = H_1N1, HH₂ = H_2N2, HH₃ = H_3N3, то этот треугольник гомотетичен треугольнику H₁H₂H₃ с центром гомотетии — серединой отрезка OE ( E — центр окружности Эйлера) и коэффициентом гомотетии k =

Свойство 1. Вершины треугольника ABC делят дуги N_2N3, N_3N1, N_1N2 пополам.

Доказательство. Действительно, ∠ N_2N1A = ∠ N_3N1A.

Свойство 2. Высоты треугольника ABC принадлежат биссектрисам внутренних углов треугольника N_1N2N3.

Доказательство. Действительно, это следует из свойства 1.

Свойство 3. Радиус OA перпендикулярен отрезкам N_2N3 и H₂H₃.

Доказательство. Действительно, это следует из свойства 1.

Свойство 4. Точка, симметричная ортоцентру H относительно середины M₁ отрезка BC принадлежит окружности, описанной около треугольника

Доказательство. Проведём диаметр AA₁ (рис.6) и найдём точку X, гомотетичную точке A₁. Поскольку A₁X = XH, то отрезок OX — средняя линия треугольника

AA₁H. Значит, он параллелен AH и равен

AH, то есть OX = OM₁ и точка X совпадает с точкой M₁ — серединой отрезка BC.

Свойство 5. Прямая Эйлера. Центроид M треугольника ABC принадлежит отрезку OH.

Доказательство. Проведём отрезок AM₁ (рис. 6). Он пересечёт OH в точке Y. Поскольку то M₁M : AM = 1 : 2, а значит, точка Y совпадает с точкой M₁.

Окружность девяти точек

Около треугольника H₁H₂H₃ опишем окружность γ_e. Её центр делит пополам отрезок OH (точка E). Середины отрезков AH, BH, CH (точки E₁, E₂, E₃) гомотетичны точкам A, B и C и принадлежат окружности γ_e.

Докажем, что точки M₁, M₂, M₃ принадлежат окружности γ_e.

Доказательство. Действительно, точки A₁ и H симметричны относительно точки B. Кроме того, точки A₁ и M₁ гомотетичны, а значит, точка M₁ принадлежит окружности γ_e.

ІІІ. Ортоцентрический треугольник Q₁Q₂Q₃

Опишем окружность около треугольника ABC и построим точки W₁,W₂, W₃ (середины дуг BC, AC, AB) (рис. 7).

Точку пересечения хорд W₂W₃ и AW₁ обозначим Q₁. Аналогично получим точки Q₁ и Q₃. По теореме «листа трилистника» имеем: IW₁ = W₁C. Поскольку ∪ AW₂ = ∪ W₂C, то

Поскольку окружность, описанная около треугольника Q₁Q₂Q₃, есть окружность Эйлера треугольника W₁W₂W₃, то девять точек принадлежат одной окружности: середины отрезков W₁W₃, W₂W₃, W₁W₂, IW₁, IW₂, IW₃, IA, IB, IC.

ІV. Ортоцентрический треугольник ABC Рассмотрим треугольник, вершины которого — центры вневписанных окружностей I_a, Ib, I_c (рис.8).

Ортоцентрическим треугольником этого

треугольника будет треугольник ABC, так как

каждая из его вершин есть пересечение внутренней и внешней биссектрис. Поскольку радиус окружности, описанной около треугольника ABC будет R, то радиус окружности, описанной около треугольника I_aIbI_c будет 2R, а площадь S_IaIbIc=2R⋅p.

Поскольку окружность, описанная около треугольника ABC, является окружностью Эйлера треугольника I_aIbI_c, то девять точек принадлежат одной окружности: вершины треугольника ABC, точки W₁, W₂, W₃, середины

V. Треугольник, подобный ортоцентрическому треугольнику H₁H₂H₃

Через вершины A, B и C проведём касательные к окружности, описанной около треугольника ABC. Получим треугольник T₁T₂T₃ (рис. 9).

тангенциальным) вычисляют по формуле:

S_T=R⋅p_T, где R — радиус окружности, вписанной в треугольник T₁T₂T₃.

Глава 2. Применение.

§ 1 Применение свойств ортотреугольника для решения задач

Задача 1.

Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?

Следствием данной задачи будет следующее утверждение: каждая сторона ортотреугольника равна произведению противолежащей стороны на косинус противолежащего угла исходного треугольника.

Задача 2.

Треугольник АВС остроугольный, и угол ВАС равен α. На стороне ВС как на диаметре построена полуокружность, пересекающая стороны АВ и АС в точках Р и Q соответственно. Найдите отношение площадей треугольников АВС и APQ.

Задача 3

В остроугольном треугольнике АВС проведены высоты АD, ВЕ и СF. Докажите, что pR=Pr, где p-периметр треугольника EDF, Р – периметр треугольника АВС.

Решение(без применения свойств):

Решение(без применения свойств):

Задача 4

Задача 5.

Задача 6

В равнобедренном треугольнике ABC(AB = BC)проведены высоты AA₁,

Глава 3. Анкетирование учащихся

Всем ученикам 10 и 11 классов я задала по 4 вопроса:

Знаете ли вы об ортоцентрических треугольниках?

Применяли ли вы свойства ортоцентрических треугольников при решении задач?

Как вы считаете, можно ли облегчить решение задач, используя эти свойства?

Хотели бы вы научиться решать задачи на применение свойств ортоцентрических треугольников?

Подсчитав ответы «да», я получила следующие результаты:

Источник