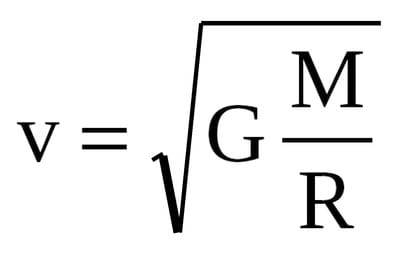что такое орбитальная скорость планеты
Орбитальная скорость
Орбитальная скорость тела (обычно планеты, естественного или искусственного спутника, кратной звезды) — это скорость, с которой оно вращается вокруг барицентра системы, как правило вокруг более массивного тела.
Определение
В полярных координатах выражение для орбитальной скорости (
Орбитальная скорость также может вычисляться по следующим формулам:
Орбиты Земли
| Орбита | Расстояние между центрами масс | Высота над поверхностью Земли | Орбитальная скорость | Орбитальный период | specific orbital energy (англ.) |
|---|---|---|---|---|---|
| Поверхность Земли, для сравнения | 6,400 км | 0 км | 7.89 км/с | — | -62.6 MJ/kg |
| Низкая опорная орбита | 6,600 — 8,400 км | 200 — 2,000 км | Круговая орбита: 6.9 — 7.8 км/с эллиптическая орбита: 6.5 — 8.2 км/с | 89 — 128 мин | -17.0 MJ/kg |
| Высокоэллиптическая орбита спутников Молния | 6,900 — 46,300 км | 500 — 39,900 км | 1.5 — 10.0 км/с | 11 ч 58 мин | -4.7 MJ/kg |
| Геостационарная орбита | 42,000 км | 35,786 км | 3.1 км/с | 23 ч 56 мин | -4.6 MJ/kg |
| Орбита Луны | 363,000 — 406,000 км | 357,000 — 399,000 км | 0.97 — 1.08 км/с | 27.3 дней | -0.5 MJ/kg |
Примечания
| Основные | Box-орбита • Орбита захвата • Эллиптическая орбита / Высокая эллиптическая орбита • Орбита ухода • Орбита захоронения • Гиперболическая траектория • Наклонная орбита / Ненаклонная орбита • Оскулирующая орбита • Параболическая траектория • Опорная орбита (в т.ч. низкая) • Синхронная орбита • (Полусинхронная • Субсинхронная) • Стационарная орбита |
| Геоцентрические | Геосинхронная орбита • Геостационарная орбита • Солнечно-синхронная орбита • Низкая околоземная орбита • Средняя околоземная орбита • Высокая околоземная орбита • Молния-орбита • Околоэкваториальная орбита • Орбита Луны • Полярная орбита • Тундра-орбита • TLE |
| Вокруг других небесных тел и точек | Ареосинхронная орбита • Ареостационарная орбита • Гало-орбита • Орбита Лиссажу • Окололунная орбита • Гелиоцентрическая орбита • Солнечно-синхронная орбита |
| Классические |  Наклонение · Наклонение ·  Долгота восходящего узла · Долгота восходящего узла ·  Эксцентриситет · Эксцентриситет ·  Аргумент перицентра · Аргумент перицентра ·  Большая полуось · Большая полуось ·  Средняя аномалия на эпоху Средняя аномалия на эпоху |
| Другие |  Истинная аномалия · Истинная аномалия ·  Малая полуось · Малая полуось ·  Эксцентрическая аномалия · Эксцентрическая аномалия ·  Средняя долгота · Средняя долгота ·  Истинная долгота · Истинная долгота ·  Период обращения Период обращения |
 Небесная механика Небесная механика | |
|---|---|
| Законы и задачи | Законы Ньютона • Закон всемирного тяготения • Законы Кеплера • Задача двух тел • Задача трёх тел • Гравитационная задача N тел • Задача Бертрана • Уравнение Кеплера |
| Небесная сфера | Система небесных координат: галактическая • горизонтальная • первая экваториальная • вторая экваториальная • эклиптическая • Международная небесная система координат • Сферическая система координат • Ось мира • Небесный экватор • Прямое восхождение • Склонение • Эклиптика • Равноденствие • Солнцестояние • Фундаментальная плоскость |
| Параметры орбит | Кеплеровы элементы орбиты: эксцентриситет • большая полуось • средняя аномалия • долгота восходящего узла • аргумент перицентра • Апоцентр и перицентр • Орбитальная скорость • Узел орбиты • Эпоха |
| Движение небесных тел | Движение Солнца и планет по небесной сфере • Эфемериды Конфигурации планет: противостояние • квадратура • парад планет • Кульминация • Сидерический период • Орбитальный резонанс • Период вращения • Предварение равноденствий • Синодический период • Сближение Затмение: солнечное затмение • лунное затмение • сарос • Метонов цикл • Покрытие • Прохождение • Либрация • Элонгация • Эффект Козаи • Эффект Ярковского • Эффект Джанибекова |
| Астродинамика | |
| Космический полёт | Космическая скорость: первая (круговая) • вторая (параболическая) • третья • четвёртая Формула Циолковского • Гравитационный манёвр • Гомановская траектория • Метод оскулирующих элементов • Приливное ускорение • Изменение наклонения орбиты • Стыковка • Точки Лагранжа • Эффект «Пионера» |
| Орбиты КА | Геостационарная орбита • Гелиоцентрическая орбита • Геосинхронная орбита • Геоцентрическая орбита • Геопереходная орбита • Низкая опорная орбита • Полярная орбита • Тундра-орбита • Солнечно-синхронная орбита • Молния-орбита • Оскулирующая орбита |
Полезное
Смотреть что такое «Орбитальная скорость» в других словарях:
орбитальная скорость — orbitinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Greitis, kuriuo kūnas arba dalelė juda tam tikra orbita. atitikmenys: angl. orbital velocity vok. orbitale Geschwindigkeit, f rus. орбитальная скорость, f pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
орбитальная скорость — orbitinis greitis statusas T sritis fizika atitikmenys: angl. orbital velocity vok. orbitale Geschwindigkeit, f rus. орбитальная скорость, f pranc. vitesse orbitale, f … Fizikos terminų žodynas
Орбитальная позиция — Запрос «Точка стояния» перенаправляется сюда; см. также другие значения. Точка стояния или Орбитальная позиция положение спутника, находящегося на геостационарной орбите. Поскольку спутник, находящийся на … Википедия
Космическая скорость — (первая v1, вторая v2, третья v3 и четвёртая v4) это мин … Википедия
Третья космическая скорость — Третья космическая скорость минимальная скорость, которую необходимо сообщить находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы[1][2]. При… … Википедия
Четвёртая космическая скорость — Млечный путь Четвёртая космическая скорость минимально необходимая скорость тела, позволяющая преодолеть притяжение … Википедия
Геостационарная орбита — (ГСО) круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси. В горизонтальной системе… … Википедия
Большая полуось — это один из основных геометрических параметров объектов, образованных посредством конического сечения. Содержание 1 Эллипс 2 Парабола 3 Гипербола … Википедия
Орбитальная скорость планет
Скорость орбитального движения планет связана с их расстоянием от Солнца. Самая ближайшая к светилу планета Меркурий имеет наибольшую скорость, в то время как Плутон (карликовая планета), наоборот, наименьшую в Солнечной системе. Попробуем разобраться, что это такое и чему равна орбитальная скорость.
Что такое скорость орбитального движения?
Орбитальная скорость – скорость, с которой небесное тело вращается вокруг более массивного объекта. Этот термин может использоваться для обозначения средней орбитальной скорости планеты либо ее мгновенной скорости в какой-либо точке орбиты.
В космосе гравитация обеспечивает силу, под воздействием которой спутники вращаются по орбитам вокруг более крупных небесных тел. Под орбитой понимают траекторию движения, по которой объект движется вокруг светила. Орбита – вовсе не окружность, как считают некоторые люди. Она даже не напоминает овал, так как существует множество факторов, влияющих на движение небесных тел. Bce орбитальные пути кажутся вытянутыми, поскольку сформированы не в виде круга.
Не все орбиты планет находятся в одной плоскости. Некоторые выбиваются из нее. К примеру, если изобразить орбиты Венеры и Земли, то они имеют несколько точек пересечения. Солнце не всегда располагается в центре орбиты планеты, которая вращается вокруг него.
Орбитальная скорость планет может немного изменяться. Это зависит от того, какие объекты проходят в непосредственной близости. Особенно это очевидно на примере Красной планеты: каждый раз, когда Марс проходит рядом с Юпитером, он замедляется из-за притяжения гравитационным полем Юпитера.
Как же определить величину этой скорости? Все просто – ее можно рассчитать, используя закон тяготения и второй закона Ньютона. Эти законы сделались столь привычными, что может показаться, будто в движении космических объектов можно многое предугадать, руководствуясь вышеупомянутыми законами. Но на самом деле все не так. Порой расчеты приводят к результатам, вовсе не похожим на те, которые мы считали чуть ли не очевидными. Спутник движется по своей орбите со скоростью, которая может немного меняться.
Плутон, планета (карликовая) с наименьшей орбитальной скоростью.
Изображение с сайта ru.wikipedia.org
4glaza.ru
Август 2021
Статья одобрена экспертом: Марина Атланова
Использование материала полностью для общедоступной публикации на носителях информации и любых форматов запрещено. Разрешено упоминание статьи с активной ссылкой на сайт www.4glaza.ru.
Производитель оставляет за собой право вносить любые изменения в стоимость, модельный ряд и технические характеристики или прекращать производство изделия без предварительного уведомления.
Другие обзоры и статьи о телескопах и астрономии:
Обзоры оптической техники и аксессуаров:
Статьи о телескопах. Как выбрать, настроить и провести первые наблюдения:
Все об основах астрономии и «космических» объектах:
Этот термин может использоваться для обозначения либо средней орбитальной скорости, то есть средней скорости по всей орбите, либо ее мгновенной скорости в определенной точке ее орбиты. Максимальная (мгновенная) орбитальная скорость возникает в перицентре (перигей, перигелий и т. Д.), А минимальная скорость для объектов на замкнутых орбитах происходит в апоапсисе (апогей, афелий и т. Д.). В идеальных системах из двух тел объекты на открытых орбитах продолжают вечно замедляться по мере увеличения расстояния до центра масс.
СОДЕРЖАНИЕ
Радиальные траектории
Далее предполагается, что система представляет собой систему из двух тел, а вращающийся вокруг объекта имеет незначительную массу по сравнению с более крупным (центральным) объектом. В реальной орбитальной механике в центре внимания находится барицентр системы, а не более крупный объект.
Средняя орбитальная скорость
или полагая r равным радиусу орбиты
Средняя орбитальная скорость уменьшается с увеличением эксцентриситета.
Мгновенная орбитальная скорость
Для мгновенной орбитальной скорости тела в любой заданной точке его траектории учитываются как среднее расстояние, так и мгновенное расстояние:
Для Земли в перигелии это значение составляет:
<\ text
<\ text < м>> / <\ текст >>
Касательные скорости на высоте
Планеты
Чем ближе объект к Солнцу, тем быстрее ему нужно двигаться, чтобы поддерживать орбиту. Объекты движутся быстрее всего в перигелии (ближайшем приближении к Солнцу) и медленнее всего в афелии (самом дальнем расстоянии от Солнца). Поскольку планеты Солнечной системы находятся на почти круговых орбитах, их индивидуальные орбитальные скорости не сильно различаются. Поскольку Меркурий находится ближе всего к Солнцу и имеет наиболее эксцентричную орбиту, его орбитальная скорость варьируется от 59 км / с в перигелии до 39 км / с в афелии.
| Планета | Орбитальная скорость |
|---|---|
| Меркурий | 47,9 км / с |
| Венера | 35.0 км / с |
| Земля | 29,8 км / с |
| Марс | 24,1 км / с |
| Юпитер | 13,1 км / с |
| Сатурн | 9,7 км / с |
| Уран | 6,8 км / с |
| Нептун | 5,4 км / с |
Космические скорости: насколько быстро нужно лететь, чтобы покинуть Землю, планетную систему и галактику?
Несмотря на то, что отечественная космонавтика переживает не лучшие, мягко говоря, времена, космосом на сегодняшний день интересуется все больше людей разного возраста и уровня образования. Усилиями частных инвесторов и популяризаторов науки пространство за пределами нашей планеты становится все более интересным, доступным и понятным, привлекая любознательных граждан к получению новых знаний.
В этом материале мы кратко, избегая сложных пояснений и формулировок, расскажем о космических скоростях, которые необходимы для преодоления гравитационных полей астрономических объектов. В новостных сюжетах мы часто слышим такое словосочетание, как «первая (вторая, третья, четвертая) космическая скорость», однако далеко не каждый обыватель понимает о каких скоростях идет речь и как их определяют.
Что такое космическая скорость
Космическими скоростями в космонавтике (речь идет не только о пилотируемых полетах, но для удобства мы будем называть все запуски искусственных космических аппаратов космонавтикой) пользуются для расчета минимально необходимой скорости для:
1. Выхода космических аппаратов на орбиту Земли;
2. Выхода космических аппаратов за пределы гравитационного поля Земли;
3. Выхода космических аппаратов за пределы Солнечной системы;
4. Выхода космических аппаратов за пределы галактики Млечный Путь.
Естественно, формулы расчета космических скоростей применимы не только к нашей планете, но и к любому другому объекту Вселенной, однако мы рассмотрим лишь актуальные для земных космических аппаратов значения.
Первая космическая скорость — 7,9 км/сек
Чтобы вращаться на орбите Земли, спутнику необходимо иметь первую космическую или круговую скорость, которая для нашей планеты равна примерно 7,9 км/сек. В этом случае объект на орбите будет удерживать сила, называемая в народе центробежной, а движение Земли и сила притяжения не позволят спутнику покинуть гравитационное поле планеты.
Отсюда следует довольно интересное и простое умозаключение: что будет если в формуле расчета первой космической скорости (V1 = (GM/R) в степени 1/2, где M — масса объекта, R — радиус, а G — гравитационная постоянная) поиграть с цифрами и подставить данные, которые определят первую космическую скорость для выдуманного нами объекта, как равную скорости света (чуть менее 300 000 км/сек)?
Мы получим объект огромной массы и малого радиуса, на который свет может падать, но покинуть его гравитационное поле фотоны уже не в состоянии, ведь для этого нужна вторая космическая скорость, которая в данном случае будет превышать скорость света, что невозможно в известной нам Вселенной. Это есть объект, о котором слышал каждый и который астрофизики называют «черной дырой».
Вторая космическая скорость — 11,2 км/сек
В 1959 году в СССР состоялся запуск автоматической межпланетной станции Луна-1 — первого искусственного объекта, покинувшего гравитационное поле Земли и ставшего спутником Солнца. Для этого аппарату пришлось разогнаться до второй космической скорости (она же скорость убегания), которая для Земли составляет порядка 11,2 км/сек. Покинув Землю на такой скорости, объект выходит на параболическую орбиту, которая при условии отсутствия других тел во Вселенной позволила бы ему бесконечно далеко удалиться от планеты.
Третья космическая скорость — 16,6 км/сек
Определить точное значение третьей космической скорости невозможно, так оно может колебаться в довольно широком диапазоне. Имеет значение угол направления запуска к траектории движения Земли по орбите и контакт с гравитационными полями других планет, которые могут как ускорять, так и притормаживать КА. Минимальное значение третьей космической скорости оценивается как 16,6 км/сек.
Четвертая космическая скорость — 400-600 км/сек
Редко употребляемый термин ввиду недосягаемости определяемых им величин для нашей космонавтики в обозримом будущем. Четвертая космическая скорость подразумевает вылет КА за пределы галактики, что в принципе невозможно при текущем и ожидаемом уровне развития технологий. Учитывая, что наша Солнечная система вращается вокруг галактического центра со скоростью около 220 км/сек, примерную расчетную скорость искусственного аппарата для вылета за пределы Млечного Пути можно определить как 400-600 км/сек.
Пожалуйста, оцените статью
Средняя оценка / 5. Количество оценок:
Оценок пока нет. Поставьте оценку первым.
Интересно, спасибо за статью)
А что же тогда, говорят, что Вояджер — первый, что покинуло СС
вообще-то размер СС составляет около 0,0015 световых лет.
Солнечная система не ограничена орбитами планет.
Вояджер разогнали до 42 км в сек. Для этого использовали удачное расположение тяжелых планет Юпитер, Сатурн, Нептун.
Вояджер уже был хорошо разогнан до Юпитера. И + притяжение Юпитера добавило скорости. Пролетаю около Юпитера по кривой, Вояджер был подхвачен Ураном или Сатурном. Точно не помню.
Говорят что кур доят, Вояджер всего лишь покинул сферу солнечного ветра
Сфера солнечного ветра — Нобелевскую премию за это определение, мужики-то не знали)))
Покинуть можно с любой скоростью, если будет постоянно работать двигатель.Это всё скорости свободного полёта, когда отключены двигатели.
А это вообще двоечник написал «В 2013 году Вояджер-1, преодолев более 18 млрд километров и набрав скорость около 17 км/сек»
не набрав 17 км/с, а потеряв до 17 км/с. Потому что в 1990 году Вояджер чесал больше 25 км/с, но постепенно замедляется притяжением Солнца.
То есть есть шанс что вояджеры вообще никуда не улетят и солнце замедлит их скорость удаления до нуля и притянет обратно?
Этот термин может использоваться для обозначения либо средней орбитальной скорости, то есть средней скорости по всей орбите, либо ее мгновенной скорости в определенной точке ее орбиты. Максимальная (мгновенная) орбитальная скорость возникает в перицентре (перигей, перигелий и т. Д.), А минимальная скорость для объектов на замкнутых орбитах происходит в апоапсисе (апогей, афелий и т. Д.). В идеальных системах из двух тел объекты на открытых орбитах продолжают вечно замедляться по мере увеличения расстояния до центра масс.
СОДЕРЖАНИЕ
Радиальные траектории
Далее предполагается, что система представляет собой систему из двух тел, а вращающийся вокруг объекта имеет незначительную массу по сравнению с более крупным (центральным) объектом. В реальной орбитальной механике в центре внимания находится барицентр системы, а не более крупный объект.
Средняя орбитальная скорость
или полагая r равным радиусу орбиты
Средняя орбитальная скорость уменьшается с увеличением эксцентриситета.
Мгновенная орбитальная скорость
Для мгновенной орбитальной скорости тела в любой заданной точке его траектории учитываются как среднее расстояние, так и мгновенное расстояние:
Для Земли в перигелии это значение составляет:
<\ text
<\ text < м>> / <\ текст >>
Касательные скорости на высоте
Планеты
Чем ближе объект к Солнцу, тем быстрее ему нужно двигаться, чтобы поддерживать орбиту. Объекты движутся быстрее всего в перигелии (ближайшем приближении к Солнцу) и медленнее всего в афелии (самом дальнем расстоянии от Солнца). Поскольку планеты Солнечной системы находятся на почти круговых орбитах, их индивидуальные орбитальные скорости не сильно различаются. Поскольку Меркурий находится ближе всего к Солнцу и имеет наиболее эксцентричную орбиту, его орбитальная скорость варьируется от 59 км / с в перигелии до 39 км / с в афелии.
| Планета | Орбитальная скорость |
|---|---|
| Меркурий | 47,9 км / с |
| Венера | 35.0 км / с |
| Земля | 29,8 км / с |
| Марс | 24,1 км / с |
| Юпитер | 13,1 км / с |
| Сатурн | 9,7 км / с |
| Уран | 6,8 км / с |
| Нептун | 5,4 км / с |