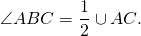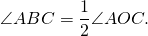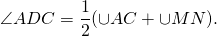что такое описанный угол
Окружность. Основные теоремы
Определения
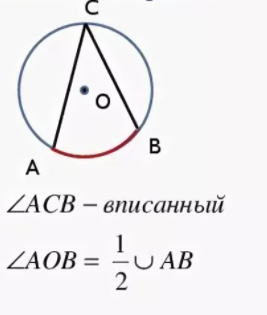
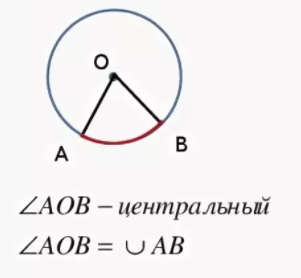
Центральный угол – это угол, вершина которого лежит в центре окружности.
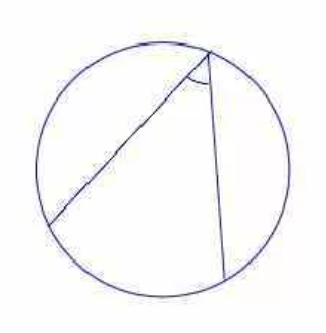
Вписанный угол – это угол, вершина которого лежит на окружности.
Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.
Теорема
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Доказательство
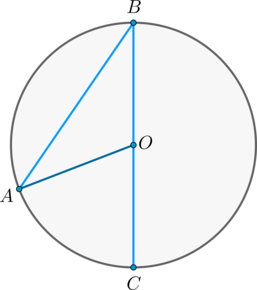
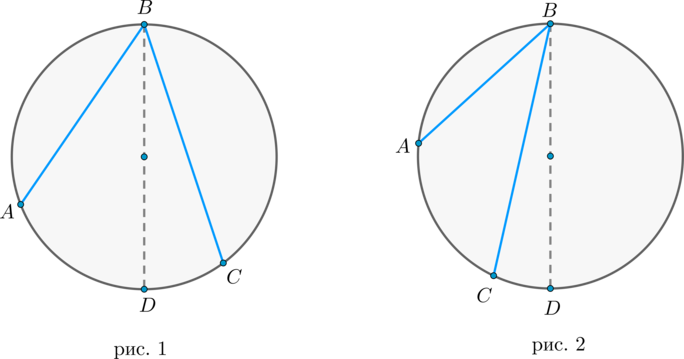
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:
1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\) (для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.
Следствия
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
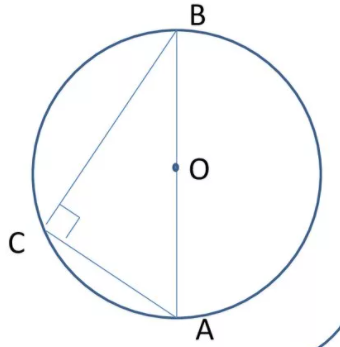
2. Вписанный угол, опирающийся на полуокружность, прямой.
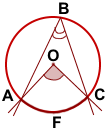
3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
Определения
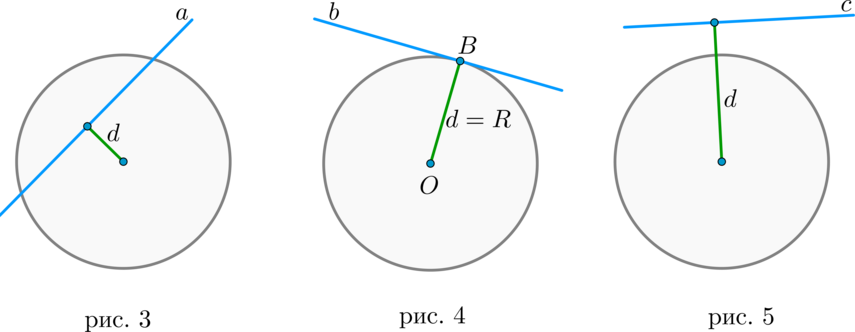
Существует три типа взаимного расположения прямой и окружности:
1) прямая \(a\) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\) от центра окружности до прямой меньше радиуса \(R\) окружности (рис. 3).
2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).
3) прямая \(c\) не имеет общих точек с окружностью (рис. 5).
Теорема
1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.
Следствие
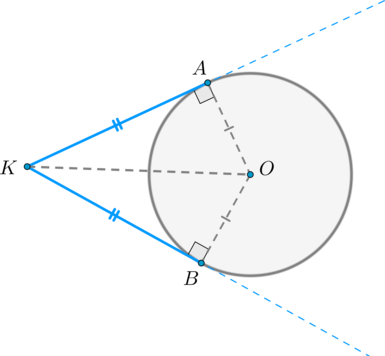
Отрезки касательных, проведенных из одной точки к окружности, равны.
Доказательство
Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\) :
Следствие
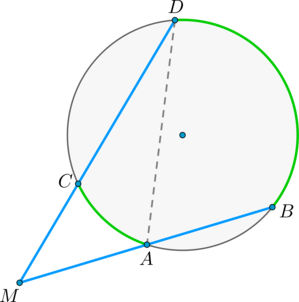
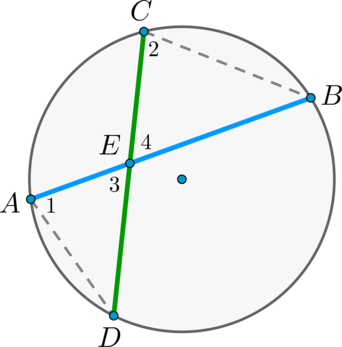
Теорема об угле между секущими
Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.
Доказательство
Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:
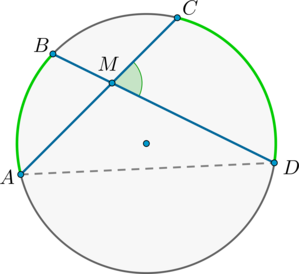
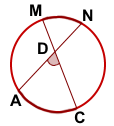
Теорема об угле между пересекающимися хордами
Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: \[\angle CMD=\dfrac12\left(\buildrel\smile\over
Доказательство
\(\angle BMA = \angle CMD\) как вертикальные.
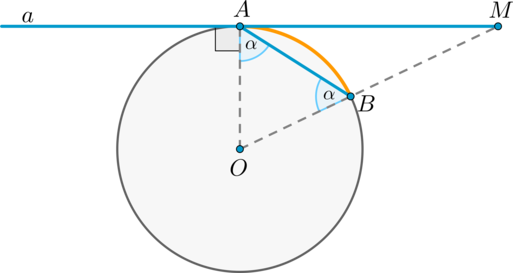
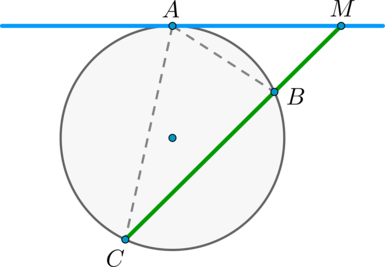
Теорема об угле между хордой и касательной
Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.
Доказательство
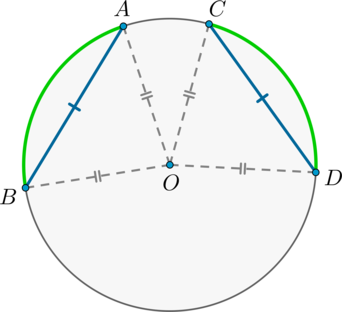
Теорема о дугах, стягиваемых равными хордами
Равные хорды стягивают равные дуги, меньшие полуокружности.
И наоборот: равные дуги стягиваются равными хордами.
Доказательство
Теорема
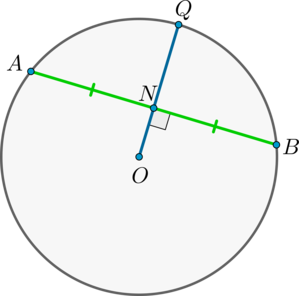
Если радиус делит хорду пополам, то он ей перпендикулярен.
Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.
Доказательство
Теорема о произведении отрезков хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство
Теорема о касательной и секущей
Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.
Доказательство
Следствие
Углы в окружности
Рассмотрим углы в окружности и углы, связанные с окружностью.
I. Угол с вершиной в центре окружности называется центральным углом.
Стороны центрального угла разбивают окружность на две части. Дугой, соответствующей данному центральному углу, называется та часть, которая содержится внутри угла.
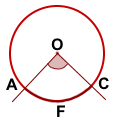
Градусная мера дуги окружности равна градусной мере соответствующего центрального угла:
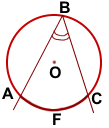
Стороны вписанного угла также разбивают окружность на две дуги. Говорят, что вписанный угол опирается на лугу, которая лежит внутри него.
Например, вписанный угол ABC опирается на дугу AC (или дугу AFC).
Вписанный угол равен половине дуги, на которую он опирается:
Есть другой вариант формулировки свойства вписанного угла.
И наоборот: любой прямой вписанный угол опирается на полуокружность.
Другая формулировка этого утверждения:
(обратно: Если вписанный угол прямой, то он опирается на диаметр).
III. Угол, вершина которого лежит в окружности — это угол между пересекающимися хордами.
Угол между пересекающимися хордами равен полусумме дуг, заключённых между его сторонами и сторонами вертикального ему угла.
IV. Угол с вершиной вне окружности, обе стороны которого пересекают окружность — это угол между секущими, которые пересекаются вне окружности.
Угол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Теорема 4:
Равные хорды стягивают равные дуги.
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Вписанные и центральные углы, их свойства
теория по математике 📈 планиметрия
Вписанный угол
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
Свойства вписанных углов
Вписанный угол равен половине дуги, на которую он опирается.
Свойство вписанного угла №2
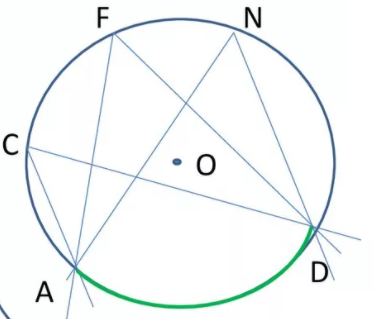
Вписанные углы, которые опираются на одну и ту же дугу, равны.
На рисунке показаны три вписанных угла – ACD, AFD, AND, которые опираются на одну и ту же дугу AD, поэтому эти углы равны.
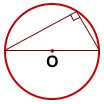
Вписанный угол, который опирается на диаметр, прямой.
Центральный угол
Центральный угол – это угол, вершина которого лежит в центре окружности.
Свойства центральных углов
Центральный угол равен дуге, на которую он опирается.
Если центральный и вписанный угол опираются на одну и ту же дугу, то вписанный угол равен половине центрального угла. И наоборот, центральный угол в 2 раза больше вписанного, если они опираются на одну и ту же дугу.
Что такое описанный угол
Центральный угол в окружности — плоский угол с вершиной в его центре.
Градусная мера дуги окружности — градусная мера соответствующего центрального угла.
Вписанный угол в окружность — угол, вершина которого лежит на окружности^ стороны пересекают эту окружность.
Доказательство теоремы о вписанном угле приводится в «Началах» Эвклида. То, что вписанный угол, опирающийся на диаметр, — прямой, знали вавилоняне еще 4000 лет назад.
Свойства вписанного угла. Радианная мера углов
Свойства вписанного угла:
1. Вписанный угoл равен половине дуги, на которую он опирается.
2. Вписанный угoл, опирающийся на диаметр, является прямым.
3. Вписaнные углы, опирающиеся на одну и ту же дугу, равны.
4. Вписaнные углы, опирающиеся на одну и ту же хорду, либо равны, либо их сумма равна 180°.
Радианная мера углов
1 радиан — центральный угол, опирающийся на дугу, равную радиусу окружности. 1 радиан = примерно 57°.
• Угол с вершиной за окружностью (стороны которого пересекают окружность) равен половине разности дуг, лежащих внутри угла.
• Угол,образованный касательной и хордой, с проведенной в точку касания, равен половине дуги, лежащей внутри угла.
• Угол между двумя касательными к окружности, проведенными через одну точку, равен половине разности дуг, ограниченных его сторонами.
Это конспект по теме «Центральный угол. Вписанный угол». Выберите дальнейшие действия: