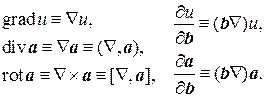что такое оператор гамильтона
Оператор Гамильтона, его использование и свойства
Лекция 16. Оператор Гамильтона, его использование и свойства. Потенциальные векторные поля, условие потенциальности. Условия независимости криволинейного интеграла второго рода от пути интегрирования. Соленоидальные и гармонические векторные поля.
Вспомним определение градиента скалярной функции u = u(x, y, z):
grad u = 
Определим оператор, стоящий в скобках в правой части этого равенства, так:
Определение 16.1. Оператор
(16.1)
называется оператором Гамильтона или набла-оператором и обозначается символом s
При применении оператора Гамильтона удобно рассматривать его как «символический вектор» и использовать различные операции над векторами. Например:
1) если умножить «вектор» sна скалярную функцию и, то получим градиент этой функ-ции: su = grad u; (16.2)
2) составив скалярное произведение s на вектор A =
s· A = 
; (16.3)
3) перемножим теперь векторы s и А векторным образом. Результатом будет ротор вектора А:
s× А = 
(16.4)
4) рассмотрим скалярное произведение векторов s и su = grad u:
s· (su) = div (grad u) = =
Определение 16.2. Оператор
Δ = s· s = s² = 
(16.5)
называется оператором Лапласа и обозначается символом Δ («дельта»).
Определение 16.3. Уравнение
(16.6)
называется уравнением Лапласа, а функция, удовлетворяющая ему – гармонической функцией.
Замечание. Отметим еще раз, результатом применения к скалярной функции и оператора Гамильтона является вектор, а оператора Лапласа – скаляр.
Потенциальные векторные поля.
Определение 16.4. Векторное поле A =
A = grad u = 
. (16.7)
При этом функция и называется потенциалом данного векторного поля.
Примерами потенциальных полей являются поле тяготения точечной массы т, помещен-ной в начале координат, электрическое поле точечного заряда е, находящегося в начале координат, и другие.
Выясним, при каких условиях векторное поле является потенциальным. Так как из (16.7) следует, что 
то 
так как смешанная производная второго порядка не зависит от порядка дифференцирования. Из этих равенств легко получаем, что
Определение 16.5. Векторное поле A =
Из предыдущих рассуждений следует, что любое потенциальное поле является безвихре-вым. Можно доказать и обратное, то есть то, что любое безвихревое поле есть поле потен-циальное.
Условия независимости криволинейного интеграла 2-го рода
от пути интегрирования.
Рассмотрим криволинейный интеграл 2-го рода 
, где L – кривая, соединяющая точки M и N. Пусть функции P(x, y) и Q(x, y) имеют непрерывные частные производные в некоторой области D, в которой целиком лежит кривая L. Определим условия, при которых рассматриваемый криволинейный интеграл зависит не от формы кривой L, а только от расположения точек M и N.
Проведем две произвольные кривые MPN и MQN, лежащие в области D и соединяющие точки M и N (рис.1).
Предположим, что
, то есть
Тогда 
, где L – замкнутый контур, состав-ленный из кривых MPN и NQM (следовательно, его можно считать произвольным). Таким образом, условие независимости криволинейного интеграла 2-го рода от пути интегриро-вания равносильно условию, что такой интеграл по любому замкнутому контуру равен нулю.
Теорема 16.1. Пусть во всех точках некоторой области D непрерывны функции P(x, y) и Q(x, y) и их частные производные 
и 
. Тогда для того, чтобы для любого замкну-того контура L, лежащего в области D, выполнялось условие
,
необходимо и достаточно, чтобы 
= 
во всех точках области D.
1) Достаточность: пусть условие 
= 
выполнено. Рассмотрим произвольный замкну-тый контур L в области D, ограничивающий область S, и напишем для него формулу Грина:
.
Итак, достаточность доказана.
2) Необходимость: предположим, что условие 
выполнено в каждой точке области D, но найдется хотя бы одна точка этой области, в которой 
– 
≠ 0. Пусть, например, в точке P(x0, y0) 
– 
> 0. Так как в левой части неравенства стоит непре-рывная функция, она будет положительна и больше некоторого δ > 0 в некоторой малой области D`, содержащей точку Р. Следовательно,
Отсюда по формуле Грина получаем, что 
, где L` – контур, ограничивающий область D`. Этот результат противоречит условию 
. Следовательно, 
= 
во всех точках области D, что и требовалось доказать.
Замечание 1. Аналогичным образом для трехмерного пространства можно доказать, что необходимыми и достаточными условиями независимости криволинейного интеграла
от пути интегрирования являются:
. (16.9)
Замечание 2. При выполнении условий (16.9) выражение Pdx + Qdy +Rdz является полным дифференциалом некоторой функции и. Это позволяет свести вычисление криволинейного интеграла к определению разности значений и в конечной и начальной точках контура интегрирования, так как
При этом функцию и можно найти по формуле
(16.10)
где (x0, y0, z0) – точка из области D, a C – произвольная постоянная. Действительно, легко убедиться, что частные производные функции и, заданной формулой (16.10), равны P, Q и R.
Пример. Вычислить криволинейный интеграл 2-го рода 
по произвольной кривой, соединяющей точки (1, 1, 1) и (2, 3, 4).
Убедимся, что выполнены условия (16.9): 
Следовательно, функция и существует. Найдем ее по формуле (16.10), положив x0 = y0 = z0 = 0. Тогда
. Таким образом, функция и определяется с точностью до произвольного постоянного слагаемого. Примем С = 0, тогда u = xyz. Следовательно, 
Соленоидальные и гармонические векторные поля.
Определение 16.6. Векторное поле A =
Замечание. Так как дивергенция характеризует плотность источников поля А, то в облас-ти, где поле соленоидально, нет источников этого поля. Примером соленоидального поля может служить поле точечного заряда е во всех точках, кроме точки, где расположен заряд.
Условием соленоидальности поля является требование, что вектор А является ротором некоторого вектора В: A = rot B. Докажем это.
Действительно, если 
, то
div A = 
Определение 16.7. Скалярное поле, задаваемое функцией u = u(x, y, z), называется гармоническим в некоторой области, если функция и в этой области удовлетворяет уравнению Лапласа: Δ и = 0.
Примеры: линейная функция, потенциал электрического поля точечного заряда или поля тяготения точечной массы.
Оператор Гамильтона и его применения
СПЕЦИАЛЬНЫЕ ВИДЫ ВЕКТОРНЫХ ПОЛЕЙ
ЛЕКЦИЯ 9
Вклад гештальтизма в развитие психологии
Гештальтизм оставил заметный след в современной психологии и оказал влияние на отношения к проблемам перцепции, научения, мышления, изучения личности, мотивации поведения, а также на развитие социальной психологии. Недавние работы, являющиеся продолжением исследований гештальтистов, позволяют предположить, что их движение еще в состоянии внести вклад в развитие науки.
Гештальт-психология, в отличие от своего главного конкурирующего научного движения – бихевиоризма, многое сохранила от своей первоначальной оригинальности, благодаря чему ее основные принципы не растворились полностью в главном направлении психологической мысли. Гештальтизм продолжал поощрять интерес к сознательному опыту даже в те годы, когда в психологии доминировали идеи бихевиоризма.
Интерес гештальтистов к сознательному опыту был не таким, как у Вундта и Титченера, он строился на основе новейших феноменологических взглядов. Современные приверженцы гештальтизма убеждены, что опыт сознания по-прежнему должен изучаться. Однако, они признают, что он не может исследоваться с той же точностью и объективностью, как обычное поведение.
В настоящее время феноменологический подход в психологии шире распространен в Европе, чем в США, но его влияние на американскую психологию можно проследить на примере ее гуманистического движения. Многие аспекты современной когнитивной психологии обязаны своим происхождением работам Вертхеймера, Коффки и Келера и тому научному движению, которое они основали около 90 лет тому назад.
Оператор Гамильтона и его применения. Дифференциальные операции второго порядка. Потенциальные поля и их свойства. Соленоидальные поля и их свойства. Гармонические поля. Уравнение Лапласа. Свойства гармонических функций.
Все дифференциальные операции векторного анализа можно весьма значительно алгебраизировать при помощи оператора Гамильтона – символического вектора Ñ (читается – «набла»), определяемого равенством
(8.1)
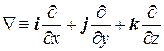
Сам по себе этот вектор смысла не имеет. Он приобретает смысл в сочетании со скалярной или векторной функцией, на которую он символически умножается в соответствии с правилами векторной алгебры.
1) Произведение Ñ на скалярную функцию u(x,y,z) дает градиент этой функции:
(8.2)
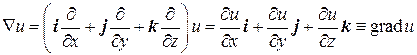
2) При помощи оператора Гамильтона, можно обобщить понятие производной по направлению. Вспомним, что для производной скалярного поля u по направлению единичного вектора b справедлива формула
.
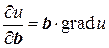
Введем скалярный дифференциальный символ:
. (8.3)
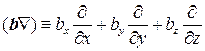
Тогда производную по направлению можно записать в виде
. (8.4)
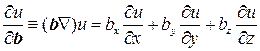
В такой записи, под b можно понимать любой вектор, не обязательно единичный.
3) По аналогии с понятием производной по направлению от скалярной функции, можно ввести понятие производной по направлению вектора b от векторной функции a:
. (8.4)
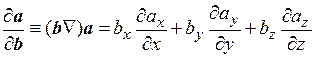
4) Скалярное произведение Ñ на векторную функцию a дает дивергенцию этой функции:
(8.5)
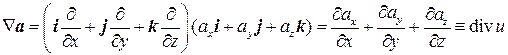
5) Векторное произведение Ñ на векторную функцию a дает ротор этой функции:
(8.6)
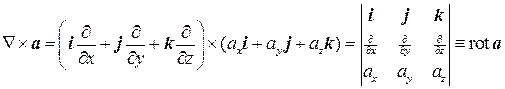
Таким образом, оператор Гамильтона и дифференциальные операции связаны следующим образом:
Пользуясь вектором Ñ, нужно помнить, что он является дифференциальным оператором, действующим на все функции, стоящие справа от него. Поэтому при преобразовании выражений, в которые входит Ñ, нужно учитывать не только правила векторной алгебры, но и правила дифференциального исчисления. Например, дифференциал произведения двух функций u и v равен
.
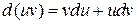
В соответствии с этим пишут
. (8.7)
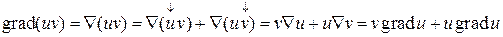
Здесь знаком «¯» отмечен тот множитель, к которому оператор Ñ должен применяться. Аналогично можно получить
. (8.8)
. (8.9)
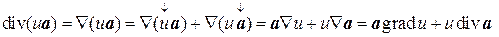
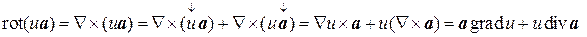
Целесообразность введения символического оператора Ñ состоит в том, что с его помощью удобно получать и записывать различные формулы векторного анализа. В частности,
, (8.10)
, (8.11)
, (8.12)
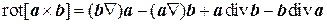
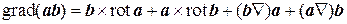
Замечание. Для вывода формулы (8.11) следует воспользоваться формулой двойного векторного произведения:
. (8.13)
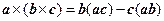
Для вывода формулы (8.12) следует предварительно найти Ñ(ac), где c=const. Поскольку c´rota=c´(Ñ´a)=Ñ(ac)–(cÑ)a, то
. (8.14)
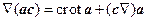
Тогда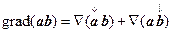 
и, далее, следует воспользоваться формулой (8.14).
Гамильтониан. Оператор энергии.
Напомним основные постулаты квантовой механики, связанные с эрмитовыми операторами:
Оператор, связанный с измерением энергии, в квантовой механике называется оператором Гамильтона или Гамильтонианом. Конкретный вид матрицы Гамильтониана зависит от деталей рассматриваемой системы. Если это система с двумя состояниями типа кубита с двумя базисными векторами, то Гамильтониан имеет вид квадратной матрицы 2х2. В общем случае он может быть и бесконечномерной матрицей.
В классической механике энергия частицы складывается из кинетической \( \displaystyle T\) и потенциальной \( \displaystyle V\). Кинетическая энергия равна:
\( \displaystyle T = \frac
Квантовомеханический аналог получается простой заменой числового значения импульса на оператор:
Сам оператор импульса в квантовомеханическом случае выражается через оператор взятия производной:
Мы получили оператор Гамильтона в координатном базисе:
Его собственные векторы также бесконечномерные — это функции от координаты x. Аппроксимируя вторую производную квадратной матрицей и прибавляя дискретизированную функцию потенциала \( \displaystyle V\) получим конечномерную матрицу, аппроксимирующую Гамильтониан:
Все что остается — это выбрать конкретный вид функции потенциала и найти на компьютере собственные векторы и собственные значения данной матрицы.
Давайте возьмем квадратичный потенциал \( \displaystyle V = kx^2\), отвечающий линейной силе в классическом случае (пружина, маятник). Система известна как гармонический осциллятор. Найдя собственные значения мы получим, что они отстоят друг от друга на одинаковом расстоянии, причем первый энергетический уровень не нулевой. Квантовый гармонический осциллятор, в отличие от классического, оказывается не может не совершать колебания (иметь нулевую энергию).
Мы наблюдаем эффект квантования. Измеренная энергия не может принимать любое значение, а только одно из разрешенных, дискретных.
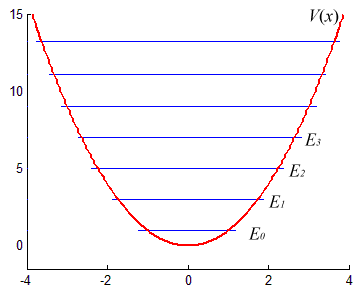
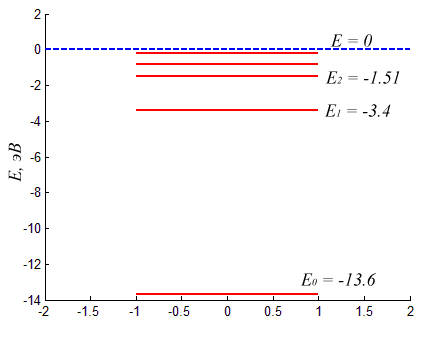
Численные величины собственных значений оператора Гамильтона зависят от вида функции потенциальной энергии. Возьмем, например, второй популярный пример — потенциал в виде прямоугольной ямы.
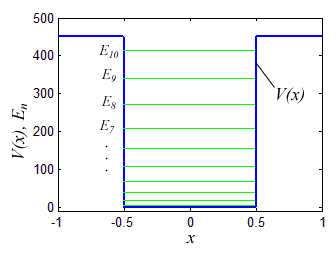
Каждому собственному значению (энергетическому уровню) соответствует собственный вектор — волновая функция в которую перейдет вектор состояния после измерения данного собственного значения (энергии). Несколько собственных функций, соответствующих нескольким первым собственным значениям Гамильтониана с прямоугольным потенциалом приведены на рисунке.
Из рисунка понятно почему квантовомеханический вектор состояния исторически получил название волновой функции. Аналогично можно найти и спектр атома водорода взяв за \( \displaystyle V(x) \) кулоновский потенциал притяжения электрона и протона:
Оператор Гамильтона выделяется среди других эрмитовых операторов тем, что он является генератором эволюции во времени вектора состояния (поэтому он входит в уравнение Шредингера). В связи с этим ряд высказываний касательно времени можно сформулировать используя Гамильтониан. Так утверждение, что величина сохраняется означает ее неизменность с течением времени. На языке оператора Гамильтона данный факт преобразуется в:
Если данный эрмитов оператор коммутирует с Гамильтонианом, то физическая величина, представляемая данным оператором, сохраняется.
То есть, если \( \displaystyle [A,H]=AH-HA=0\), то \( \displaystyle A\) сохраняется.
Тривиальный случай — это закон сохранения энергии, поскольку любой оператор коммутирует сам с собой:
\( \displaystyle [H,H]=0 \Rightarrow\) энергия сохраняется.