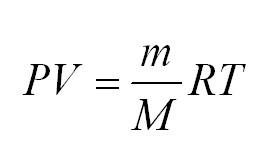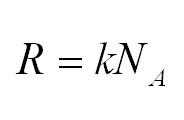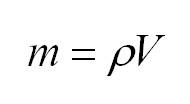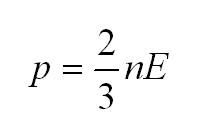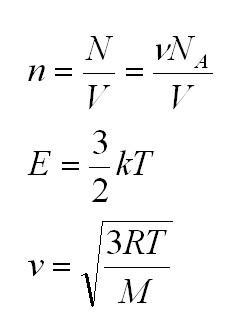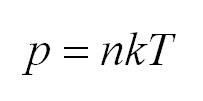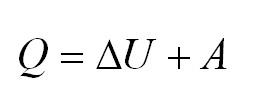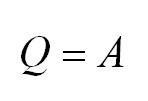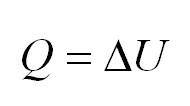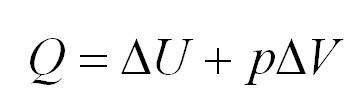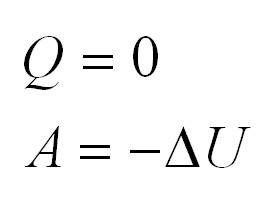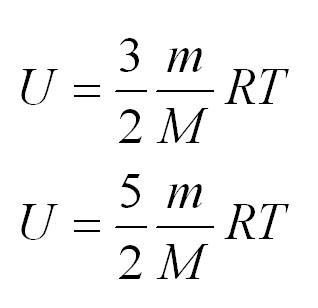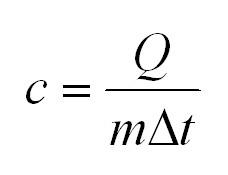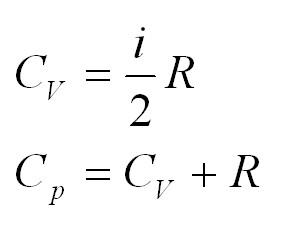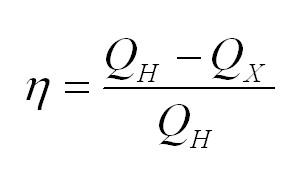что такое i в формуле внутренней энергии

Внутренняя энергия и работа идеального газа

теория по физике 🧲 термодинамика

Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.

Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:

i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.

Изменение внутренней энергии идеального газа в изопроцессах

Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной.

Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.

Работа идеального газа

Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:

Перемещение равно разности высот поршня в конечном и начальном положении:

Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:

Работа идеального газа

p — давление газа, S — площадь поршня

Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:

A ‘ = p ( V 2 − V 1 ) = p Δ V > 0

Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.

Работа идеального газа при изобарном сжатии:

A ‘ = p ( V 2 − V 1 ) = p Δ V 0

Работа идеального газа при нагревании газа:

Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.

Геометрический смысл работы в термодинамике

В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).

Примеры графических задач

Изохорное охлаждение и изобарное сжатие:

Изобарное расширение:
Изобарное сжатие:
Изохорное охлаждение:
Замкнутый цикл: 1–2: A ‘ = ( p 1 − p 3 ) ( V 2 − V 1 )
Произвольный процесс:

Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A₂ к A₁ в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:

A 2 = p ( V 2 − V 1 ) = 4 p ( 5 V − 3 V ) = 4 p 2 V = 8 p V

A 1 = p ( V 2 − V 1 ) = p ( 5 V − V ) = 4 p V

Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.

Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?

Для каждой величины подберите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10 5 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10 5 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Источник

Формула внутренней энергии

Определение и формула внутренней энергии

Внутренней энергией тела (системы) называют энергию, которая связана со всеми видами движения и взаимодействия частиц, составляющих тело (систему), включая энергию взаимодействия и движения сложных частиц.

Из выше сказанного следует, что к внутренней энергии не относят кинетическую энергию движения центра масс системы и потенциальную энергию системы, вызванную действием внешних сил. Это энергия, которая зависит только от термодинамического состояния системы.

Внутреннюю энергию чаще всего обозначают буквой U. При этом бесконечно малое ее изменение станет обозначаться dU. Считается, что dU является положительной величиной, если внутренняя энергия системы растет, соответственно, внутренняя энергия отрицательна, если внутренняя энергия уменьшается.

Внутренняя энергия системы тел равна сумме внутренних энергий каждого отдельного тела плюс энергия взаимодействия между телами внутри системы.

Внутренняя энергия – функция состояния системы. Это означает, что изменение внутренней энергии системы при переходе системы из одного состояния в другое не зависит от способа перехода (вида термодинамического процесса при переходе) системы и равно разности внутренних энергий конечного и начального состояний:

Для кругового процесса полное изменение внутренней энергии системы равно нулю:

Для системы, на которую не действуют внешние силы и находящуюся в состоянии макроскопического покоя, внутренняя энергия – полная энергия системы.

Внутренняя энергия может быть определена только с точностью до некоторого постоянного слагаемого (U₀), которое не определимо методами термодинамики. Однако, данный факт не существенен, так как при использовании термодинамического анализа, имеют дело с изменениями внутренней энергии, а не абсолютными ее величинами. Часто U_0 полагают равным нулю. При этом в качестве внутренней энергии рассматривают ее составляющие, которые изменяются в предлагаемых обстоятельствах.

Внутреннюю энергию считают ограниченной и ее граница (нижняя) соответствует T=0K.

Внутренняя энергия идеального газа

Внутренняя энергия идеального газа зависит только от его абсолютной температуры (T) и пропорциональна массе:

i – число степеней свободы молекулы идеального газа, v – число молей газа, R=8,31 Дж/(моль•К) – универсальная газовая постоянная.

Первое начало термодинамики

В более привычных формулировках первого начала термодинамики, например, формулировке Гельмгольца внутренняя энергия системы вводится как физическая характеристика системы. При этом поведение системы определено законом сохранения энергии. Гельмгольц не определяет внутреннюю энергию как функцию конкретных параметров состояния системы:

$\Delta U$ – изменение внутренней энергии в равновесном процессе, Q – количество теплоты, которое получила система в рассматриваемом процессе, A – работа, которую система совершила.

Единицы измерения внутренней энергии

Основной единицей измерения внутренней энергии в системе СИ является: [U]=Дж

Примеры решения задач

Задание. Вычислите, на какую величину изменится внутренняя энергия гелия имеющего массу 0,1 кг, если его температура увеличилась на 20С.

Решение. При решении задачи считаем гелий одноатомным идеальным газом, тогда для расчетов можно применить формулу:

$$d U=\frac <2>\nu R d T(1.1)$$

Все величины необходимые для вычислений имеются:

$\Delta U=\frac<3> <2>\cdot \frac<0,1><4 \cdot 10^<-3>> \cdot 20 \cdot 8,31=6,2 \cdot 10^<3>$ (Дж)

Формула внутренней энергии не по зубам? Тебе ответит эксперт через 10 минут!

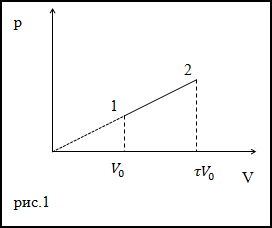
Решение. Исходя из рисунка, уравнение процесса можно представить аналитически как:

Показатель адиабаты связан с числом степеней свободы газа выражением:

Выразим число степеней свободы из (2.2):

Приращение внутренней энергии для постоянной массы газа (см. Пример 1) найдем в соответствии с формулой:

$$\Delta U=\frac <2>\nu R \Delta T(2.4)$$

Запишем уравнения состояний идеального газа для точек (1) и (2) рис.1:

Тогда приращение температуры, учитывая уравнение процесса и выражения (2.5), (2.6) найдем как:

$$ \begin \Delta T &=T-T_<0>=\frac<1><\nu R>\left(p V-p_ <0>V_<0>\right)=\frac<1><\nu R>\left(\alpha V \cdot V-\alpha V_ <0>V_<0>\right)=\\ &=\frac<1><\nu R>\left(\alpha \tau V_ <0>\cdot \tau V_<0>-\alpha V_ <0>V_<0>\right)=\frac<1> <\nu R>V_<0>^ <2>\alpha\left(\tau^<2>-1\right)(2.7) \end $$

Источник

Основные формулы термодинамики и молекулярной физики, которые вам пригодятся

Основные формулы термодинамики и молекулярной физики, которые вам пригодятся. Еще один отличный день для практических занятий по физике. Сегодня мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.

Идеальный газ

Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.

Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.

Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева

Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).

Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)

Массу, в свою очередь, можно вычислить, как произведение плотности и объема.

Основное уравнение молекулярно-кинетической теории (МКТ)

Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:

Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:

Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ

Первое начало термодинамики. Формулы для изопроцессов

Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:

Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:

Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.

Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.

Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:

Внутренняя энергия одноатомного и двухатомного идеального газа

Теплоемкость

Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.

Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.

Тепловые машины. Формула КПД в термодинамике

Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.

Коэффициент полезного действия тепловой машины вычисляется по формуле

Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Первый закон термодинамики. Как рассказать просто о сложном?

Термодинамика — раздел физики, в котором изучаются процессы изменения и превращения внутренней энергии тел, а также способы использования внутренней энергии тел в двигателях.

1. Определение первого закона термодинамики

Термодинамика — раздел физики, в котором изучаются процессы изменения и превращения внутренней энергии тел, а также способы использования внутренней энергии тел в двигателях. Собственно, именно с анализа принципов первых тепловых машин, паровых двигателей и их эффективности и зародилась термодинамика. Можно сказать, что этот раздел физики начинается с небольшой, но очень важно работы молодого французского физика Николя Сади Карно.

Самым важным законом, лежащим в основе термодинамики является первый закон или первое начало термодинамики. Чтобы понять суть этого закона, для начала, вспомним что называется внутренней энергией. ВНУТРЕННЯЯ ЭНЕРГИЯ тела — это энергия движения и взаимодействия частиц, из которых оно состоит. Нам хорошо известно, что внутреннюю энергию тела можно изменить, изменив температуру тела. А изменять температуру тела можно двумя способами:

Нам, также известно, что работа, совершаемая газом, обозначается А_г, а количество переданной или полученной внутренней энергии при теплообмене называется количеством теплоты и обозначается Q. Внутреннюю энергию газа или любого тела принято обозначать буквой U, а её изменение, как и изменение любой физической величины, обозначается с дополнительным знаком Δ, то есть ΔU.

Сформулируем ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ для газа. Но, прежде всего, отметим, что когда газ получает некоторое количество теплоты от какого-либо тела, то его внутренняя энергия увеличивается, а когда газ совершает некоторую работу, то его внутренняя энергия уменьшается. Именно поэтому первый закон термодинамики имеет вид:

Так как работа газа и работа внешних сил над газом равны по модулю и противоположны по знаку, то первый закон термодинамики можно записать в виде:

Понять суть этого закона довольно просто, ведь изменить внутреннюю энергию газа можно двумя способами: либо заставить его совершить работу или совершить над ним работу, либо передать ему некоторое количество теплоты или отвести от него некоторое количество теплоты.

2. Первый закон термодинамики в процессах

Применительно к изопроцессам первый закон термодинамики может быть записан несколько иначе, учитывая особенности этих процессов. Рассмотрим три основных изопроцесса и покажем, как будет выглядеть формула первого закона термодинамики в каждом из них.

3. Применение

Первое начало термодинамики (первый закон) имеет огромное значение в этой науке. Вообще понятие внутренней энергии вывело теоретическую физику 19 века на принципиально новый уровень. Появились такие понятия как термодинамическая система, термодинамическое равновесие, энтропия, энтальпия. Кроме того, появилась возможность количественного определения внутренней энергии и её изменения, что в итоге привело учёных к пониманию самой природы теплоты, как формы энергии.

Ну, а если говорить о применении первого закона термодинамики в каких-либо задачах, то для этого необходимо знать два важных факта. Во-первых, внутренняя энергия идеального одноатомного газа равна: 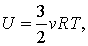а во-вторых, работа газа численно равна площади фигуры под графиком данного процесса, изображённого в координатах p—V. Учитывая это, можно вычислять изменение внутренней энергии, полученное или отданное газом количество теплоты и работу, совершённую газом или над газом в любом процессе. Можно также определять коэффициент полезного действия двигателя, зная какие процессы в нём происходят.

Источник

Учебники

Журнал «Квант»

Общие

Содержание

Внутренняя энергия тел

Согласно MKT все вещества состоят из частиц, которые находятся в непрерывном тепловом движении и взаимодействуют друг с другом. Поэтому, даже если тело неподвижно и имеет нулевую потенциальную энергию, оно обладает энергией (внутренней энергией), представляющей собой суммарную энергию движения и взаимодействия микрочастиц, составляющих тело. В состав внутренней энергии входят:

В термодинамике рассматриваются процессы при температурах, при которых не возбуждается колебательное движение атомов в молекулах, т.е. при температурах, не превышающих 1000 К. В этих процессах изменяются только первые две составляющие внутренней энергии. Поэтому

под внутренней энергией в термодинамике понимают сумму кинетической энергии всех молекул и атомов тела и потенциальной энергии их взаимодействия.

Внутренняя энергия тела определяет его тепловое состояние и изменяется при переходе из одного состояния в другое. В данном состоянии тело обладает вполне определенной внутренней энергией, не зависящей от того, в результате какого процесса оно перешло в данное состояние. Поэтому внутреннюю энергию очень часто называют функцией состояния тела.

Рассчитать внутреннюю энергию можно только для идеального газа, т.к. молекулы не взаимодействуют между собой и потенциальная энергия их равна нулю:

U = \dfrac <2>\cdot \dfrac \cdot R \cdot T,\)

где i — степень свободы. Для одноатомного газа (например, инертные газы) i = 3, для двухатомного — i = 5.

Из этих формул видно, что внутренняя энергия идеального газа зависит только от температуры и числа молекул и не зависит ни от объема, ни от давления. Поэтому изменение внутренней энергии идеального газа определяется только изменением его температуры и не зависит от характера процесса, в котором газ переходит из одного состояния в другое:

*Вывод формулы

Средняя кинетическая энергия молекулы \(

\left\langle W_k \right\rangle = \dfrac <2>\cdot k \cdot T\).

Число молекул в газе \(

N = \dfrac \cdot N_A\).

Следовательно, внутренняя энергия идеального газа

Учитывая, что k⋅N_A = R — универсальная газовая постоянная, имеем

U = \dfrac <2>\cdot \dfrac \cdot R \cdot T\) — внутренняя энергия идеального газа.

Изменение внутренней энергии

Внутренняя энергия тела может изменяться двумя способами:

Изменение внутренней энергии системы без совершения работы называется теплообменом (теплопередачей).

Существует три вида теплообмена: теплопроводность, конвекция и излучение.

а) Теплопроводностью называется процесс теплообмена между телами (или частями тела) при их непосредственном контакте, обусловленный тепловым хаотическим движением частиц тела. Амплитуда колебаний молекул твердого тела тем больше, чем выше его температура. Теплопроводность газов обусловлена обменом энергией между молекулами газа при их столкновениях. В случае жидкостей работают оба механизма. Теплопроводность вещества максимальна в твердом и минимальна в газообразном состоянии.

б) Конвекция представляет собой теплопередачу нагретыми потоками жидкости или газа от одних участков занимаемого ими объема в другие.

в) Теплообмен при излучении осуществляется на расстоянии посредством электромагнитных волн.

Рассмотрим более подробно способы изменения внутренней энергии.

Механическая работа

При рассмотрении термодинамических процессов механическое перемещение макротел в целом не рассматривается. Понятие работы здесь связывается с изменением объема тела, т.е. перемещением частей макротела друг относительно друга. Процесс этот приводит к изменению расстояния между частицами, а также часто к изменению скоростей их движения, следовательно, к изменению внутренней энергии тела.

Изобарный процесс

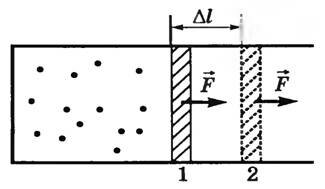
Рассмотрим вначале изобарный процесс. Пусть в цилиндре с подвижным поршнем находится газ при температуре T₁ (рис. 1).

Будем медленно нагревать газ до температуры T₂. Газ будет изобарически расширяться, и поршень переместится из положения 1 в положение 2 на расстояние Δl. Сила давления газа при этом совершит работу над внешними телами. Так как p = const, то и сила давления F = p⋅S тоже постоянная. Поэтому работу этой силы можно рассчитать по формуле

A = F \cdot \Delta l = p \cdot S \cdot \Delta l = p \cdot \Delta V,\)

где ΔV — изменение объема газа.

При расширении (ΔV > 0) газа совершается положительная работа (А > 0); при сжатии (ΔV 0) газа А ‘ 0.

Запишем уравнение Клапейрона—Менделеева для двух состояний газа:

p \cdot V_1 = \nu \cdot R \cdot T_1, \; \; p \cdot V_2 = \nu \cdot R \cdot T_2,\)

Следовательно, при изобарном процессе

Если ν = 1 моль, то при ΔΤ = 1 К получим, что R численно равна A.

Отсюда вытекает физический смысл универсальной газовой постоянной: она численно равна работе, совершаемой 1 моль идеального газа при его изобарном нагревании на 1 К.

Не изобарный процесс

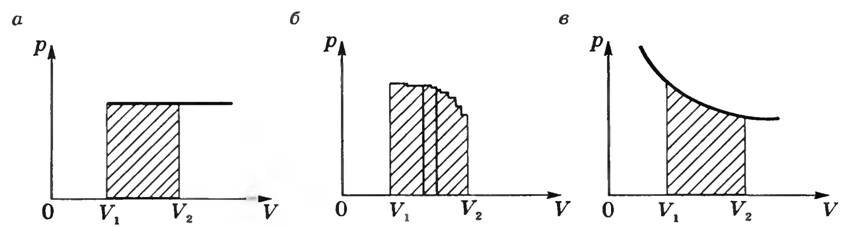
На графике p (V) при изобарном процессе работа равна площади заштрихованного на рисунке 2, а прямоугольника.

Если процесс не изобарный (рис. 2, б), то кривую функции p = f(V) можно представить как ломаную, состоящую из большого количества изохор и изобар. Работа на изохорных участках равна нулю, а суммарная работа на всех изобарных участках будет равна

A = \lim_ <\Delta V \to 0>\sum^n_ p_i \cdot \Delta V_i\), или \(

т.е. будет равна площади заштрихованной фигуры.

При изотермическом процессе (Т = const) работа равна площади заштрихованной фигуры, изображенной на рисунке 2, в.

Определить работу, используя последнюю формулу, можно только в том случае, если известно, как изменяется давление газа при изменении его объема, т.е. известен вид функции p = f(V).

Таким образом, видно, что даже при одном и том же изменении объема газа работа будет зависеть от способа перехода (т.е. от процесса: изотермический, изобарный …) из начального состояния газа в конечное. Следовательно, можно сделать вывод, что

Количество теплоты

Как известно, при различных механических процессах происходит изменение механической энергии W. Мерой изменения механической энергии является работа сил, приложенных к системе:

При теплообмене происходит изменение внутренней энергии тела. Мерой изменения внутренней энергии при теплообмене является количество теплоты.

Количество теплоты — это мера изменения внутренней энергии в процессе теплообмена.

Таким образом, и работа, и количество теплоты характеризуют изменение энергии, но не тождественны внутренней энергии. Они не характеризуют само состояние системы (как это делает внутренняя энергия), а определяют процесс перехода энергии из одного вида в другой (от одного тела к другому) при изменении состояния и существенно зависят от характера процесса.

Основное различие между работой и количеством теплоты состоит в том, что

Нагревание (охлаждение)

Опыт показывает, что количество теплоты, необходимое для нагревания тела массой m от температуры T₁ до температуры T₂, рассчитывается по формуле

где c — удельная теплоемкость вещества (табличная величина);

Единицей удельной теплоемкости в СИ является джоуль на килограмм-Кельвин (Дж/(кг·К)).

Удельная теплоемкость c численно равна количеству теплоты, которое необходимо сообщить телу массой 1 кг, чтобы нагреть его на 1 К.

Кроме удельной теплоемкости рассматривают и такую величину, как теплоемкость тела.

Теплоемкость тела C численно равна количеству теплоты, необходимому для изменения температуры тела на 1 К:

Единицей теплоемкости тела в СИ является джоуль на Кельвин (Дж/К).

Парообразование (конденсация)

Для превращения жидкости в пар при неизменной температуре необходимо затратить количество теплоты

где L — удельная теплота парообразования (табличная величина). При конденсации пара выделяется такое же количество теплоты.

Единицей удельной теплоты парообразования в СИ является джоуль на килограмм (Дж/кг).

Плавление (кристаллизация)

Для того чтобы расплавить кристаллическое тело массой m при температуре плавления, необходимо телу сообщить количество теплоты

где λ — удельная теплота плавления (табличная величина). При кристаллизации тела такое же количество теплоты выделяется.

Единицей удельной теплоты плавления в СИ является джоуль на килограмм (Дж/кг).

Сгорание топлива

Количество теплоты, которое выделяется при полном сгорании топлива массой m,

где q — удельная теплота сгорания (табличная величина).

Единицей удельной теплоты сгорания в СИ является джоуль на килограмм (Дж/кг).

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 129-133, 152-161.

Источник