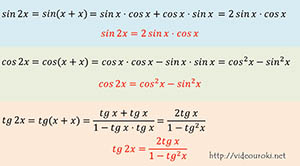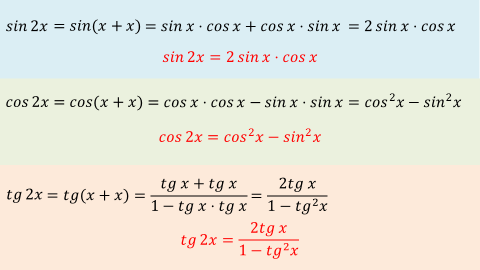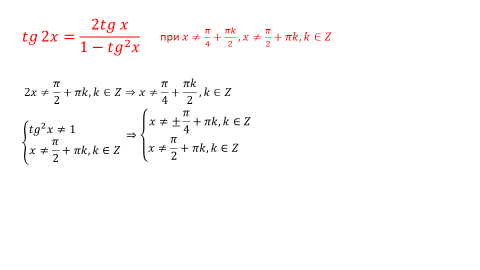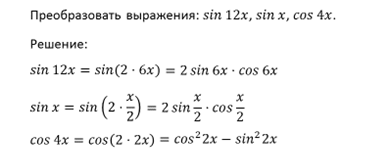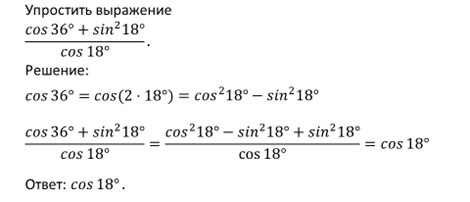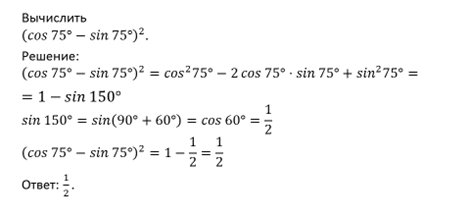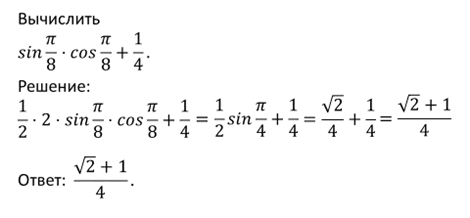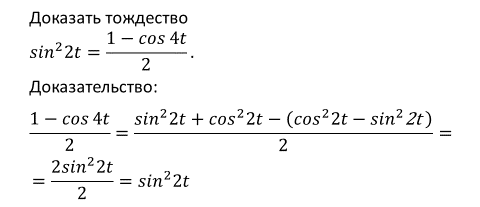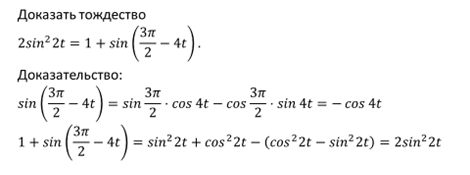Что такое формулы двойного аргумента

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №35. Формулы двойного аргумента.

Перечень вопросов, рассматриваемых в теме:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.

Теоретический материал для самостоятельного изучения

Рассмотрим выражение . Представим как и подставим в формулу синуса суммы. Получим:

(1)

Эту формулу называют синус двойного аргумента.

Например, . В этом случае .

Рассмотрим выражение , где так же . Применяем формулу косинуса суммы:

Получили формулу косинуса двойного аргумента (2)

Например,

Так как , а , то получим ещё две формулы косинуса двойного аргумента.

(3)

(4)

Рассмотрим выражение tg и с помощью формулы тангенса суммы выведем формулу тангенса двойного угла. Помним, что . Получаем:

, где (5)

Для котангенса двойного угла применяем формулу:
, где (6)

Например, .

Формулы (1)-(6) можно использовать как слева направо, так и справа налево. Аргументом может быть не только угол, но и любое выражение. Например,

Докажем формулу для тройного угла.

Представим . По формуле синуса суммы получим:

(используем формулы двойного аргумента)

(применяем формулу

Получили формулу синуса тройного угла:

(7)

Можно доказать, что косинус тройного угла вычисляется по формуле:

. (8)

Примеры и разбор решения заданий тренировочного модуля

Пример 1. Найти , если

Применим формулу (3)

Пример 2. Доказать тождество

Доказательство: Преобразуем левую часть, воспользуясь тем, что формулой (1) и формулой квадрата суммы, получаем:

Левая часть равна правой. Доказано.

Пример 3. Найти ,если

Источник

Формулы двойного аргумента

Урок 28. Алгебра 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Формулы двойного аргумента»

· познакомиться с формулами двойного аргумента;

· рассмотреть примеры использования этих формул для решения задач.

Давайте с вами ещё раз повторим основные формулы синуса, косинуса, тангенса суммы и разности аргументов.

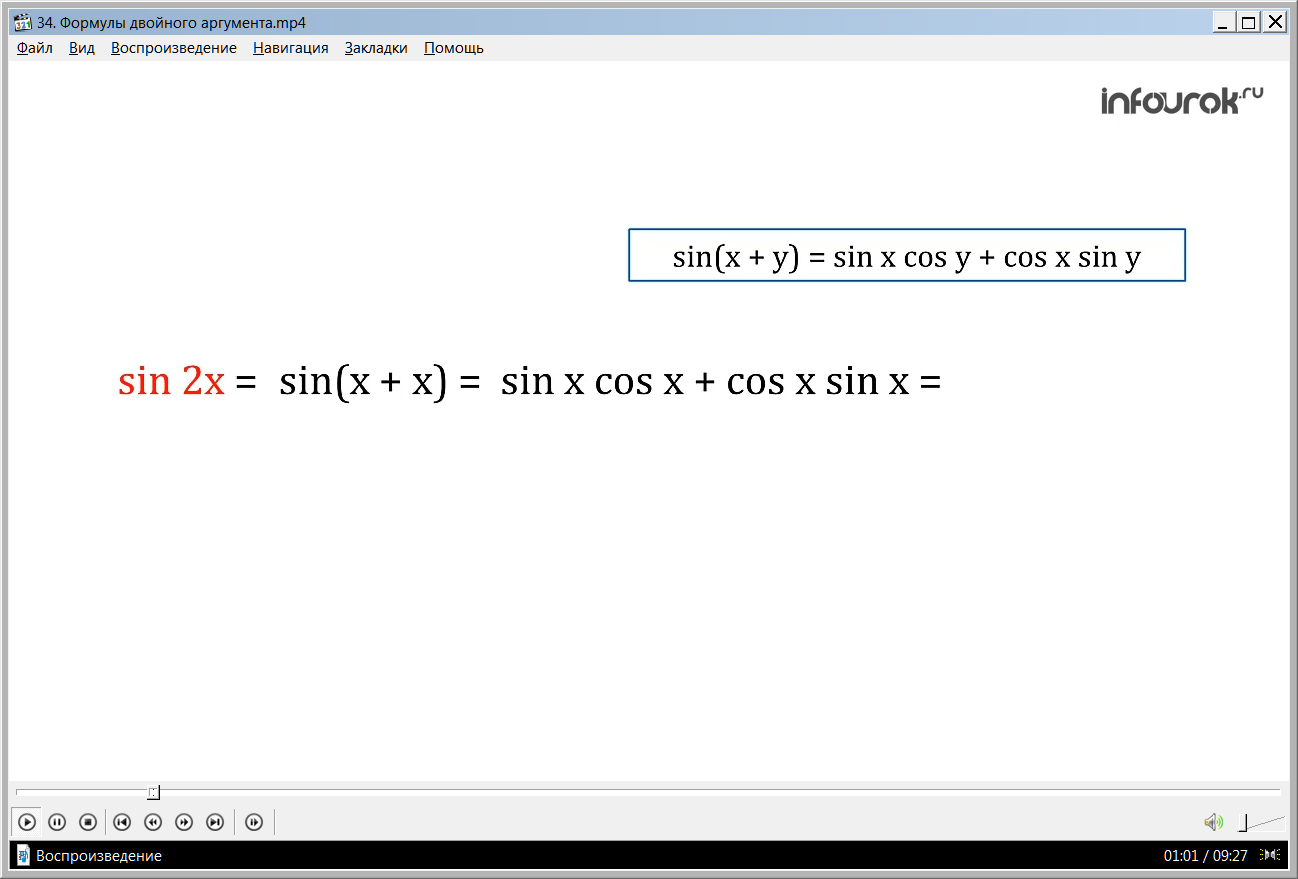
Теперь, давайте попробуем вывести формулы для вычисления sin 2x, cos 2x и tg 2x.

Если формулы синуса и косинуса двойного угла справедливы для всех x, то формула тангенса двойного угла накладывает на x определённые ограничения.

Рассмотрим примеры применения изученных формул к преобразованию выражений.

Рассмотрим ещё один пример.

Рассмотрим ещё один пример.

Рассмотрим примеры использования формул двойного аргумента для доказательств тождеств.

Рассмотрим примеры использования формул двойного аргумента для решения уравнений.

Источник

Формулы двойного и половинного аргумента. Универсальная подстановка

п.1. Формулы двойного аргумента

Выведем формулы двойного аргумента, исходя из формул суммы (см. §13 и §14 данного справочника)

\begin sin2\alpha=sin(\alpha+\alpha)=sin\alpha cos\alpha+cos\alpha sin\alpha=2sin\alpha cos\alpha\\ cos2\alpha=cos(\alpha+\alpha)=cos\alpha cos\alpha-sin\alpha sin\alpha=cos^2\alpha-sin^2\alpha\\ tg2\alpha=tg(\alpha+\alpha)=\frac<1-tg\alpha\cdot tg\alpha>=\frac<2tg\alpha> <1-tg^2\alpha>\end

Умножим полученное выражение на котангенс вверху и внизу дроби, и получим еще одно полезное выражение:

Например:
Найдем \(sin2\alpha\) и \(tg2\alpha\), если \(sin\alpha=0,8,\ \frac\pi2\lt\alpha\lt\pi\)
Угол \(\alpha\) во 2-й четверти, косинус отрицательный:
\(cos\alpha=-\sqrt<1-sin^2\alpha>=-\sqrt<1-0,8^2>=-0,6\)
\(tg\alpha=\frac=\frac<0,8><-0,6>=-\frac43\)
Синус двойного угла: \(sin2\alpha=2sin\alpha cos\alpha=2\cdot 0,8\cdot(-0,6)=-0,96\)
Тангенс двойного угла: \(tg2\alpha=\frac<2tg\alpha><1-tg^2\alpha>=\frac<2\cdot \left(-\frac43\right)><1-\left(-\frac43\right)^2>=\frac<-\frac83><1-\frac<16><9>>=\frac83 : \frac79=\frac83\cdot\frac97=\frac<24><7>=3\frac37\)

п.2. Формулы половинного аргумента

По формуле двойного аргумента для косинуса: \(cos2\alpha=2cos^2\alpha-1\)
Заменим слева угол \(2\alpha\rightarrow \alpha\), а справа угол \(\alpha\rightarrow\frac<\alpha><2>\).
Получаем: \begin cos\alpha=2cos^2\frac<\alpha><2>-1\Rightarrow 2cos^2\frac<\alpha><2>=1+cos\alpha\Rightarrow cos^2\frac<\alpha><2>=\frac<1+cos\alpha> <2>\end Из другой формулы двойного аргумента для косинуса: \(cos2\alpha=1-2sin^2\alpha\), получаем: \begin cos\alpha=1-2sin^2\frac<\alpha><2>\Rightarrow 2sin^2\frac<\alpha><2>=1-cos\alpha\Rightarrow sin^2\frac<\alpha><2>=\frac<1-cos\alpha> <2>\end Для квадрата тангенса и котангенса половинного угла: \begin tg^2\frac<\alpha><2>=\frac<2>><2>>=\frac<1-cos\alpha><1+cos\alpha>,\ \ \ ctg^2\frac<\alpha><2>=\frac<1><2>>=\frac<1+cos\alpha> <1-cos\alpha>\end

п.3. Формулы универсальной подстановки

Универсальная подстановка эффективна при решении тригонометрических уравнений, а также интегрировании.

п.4. Примеры

в) \( \sqrt<2+\sqrt<2+2cos4\alpha>> \), где \(0\le \alpha\le\frac\pi2\) \begin \sqrt<2+\sqrt<2+2cos4\alpha>>=\sqrt<2+\sqrt<2(1+cos4\alpha)>>=\sqrt<2+\sqrt<2\cdot 2cos^2 2\alpha>>=\\ =\sqrt<2+2\cdot |cos2\alpha|>=\sqrt<2(1+|cos2\alpha|)>= \left[ \begin \sqrt<2(1+cos2\alpha)>,\ \ cos2\alpha\geq 0\\ \sqrt<2(1-cos2\alpha)>,\ \ cos2\alpha\lt 0 \end \right. =\\ = \left[ \begin \sqrt<2\cdot 2cos^2\alpha>,\ \ 0\leq 2\alpha\leq\frac\pi2\\ \sqrt<2\cdot 2sin^2\alpha>,\ \ \frac\pi2\lt 2\alpha\leq \pi \end \right. = \left[ \begin 2cos\alpha,\ \ 0\leq \alpha\leq\frac\pi4\\ 2sin\alpha,\ \ \frac\pi4\lt \alpha\leq \frac\pi2 \end \right. \end Ответ: \(2cos\alpha\) при \(0\leq \alpha\leq\frac\pi4;\ \ 2sin\alpha\) при \(\frac\pi4\lt \alpha\leq \frac\pi2\)
г) \( 4(sin^4x+cos^4x)-4(sin^6x+cos^6x)-1 \)
Основное тригонометрическое тождество: \(sin^2x+cos^2x=1\)
Возведём в квадрат: \begin (sin^2x+cos^2x)^2=sin^4x+cos^4x+2sin^2x cos^2x=1\\ sin^4x+cos^4x=1-\frac<(2sinx cosx)^2><2>=1-\frac <2>\end Возведём в куб: \begin (sin^2x+cos^2x)^3=sin^6x+cos^6x+3sin2x cos^4x+3sin^4x cos^2x=1\\ sin^6x+cos^6x = 1-3sin^2x cos^2x\underbrace<(cos^2x+sin^2x)>_<=1>=\\ =1-\frac34(2sinx cosx)^2=1-\frac<3sin^2 2x> <4>\end

Подставляем: \begin 4\left(1-\frac<2>\right)-4\left(1-\frac<3sin^2 2x><4>\right)=1=4-2sin^2 2x-4+3sin^2 2x-1=\\ =sin^2 2x-1=-cos^2 2x \end Ответ: \(-cos^2 2x\)

Источник

Урок «Формулы двойного аргумента»

Краткое описание документа:

Одной из важных тем при изучении раздела тригонометрии в курсе алгебры является «Формулы двойного аргумента». Тема не является сложной, но требует достаточной внимательности, для того, чтобы понять, как следует, и использоваться правильно на практике при решении различных практических задач, уравнений, примеров на упрощение выражений и т.д.

Тригонометрия охватывает огромное количество формул, без которых невозможно справиться с практическими примерами. Тригонометрические выражения могут возникнуть не только в математике, а и в физике и механике. Чем больше формул изучил школьник, тем проще и быстрее он будет справляться, и ориентироваться во время контрольных работ из области тригонометрии в школе. Таким образом, он сможет повысить свою успеваемость и улучшить отметки.

Данная видеозапись поможет не только учителю провести интересный и познавательный урок, но и ученику, который не успевает во время урока осваивать быстро материал. С помощью электронного обучающего ресурса можно справиться и со сложными примерами, которые задаются в качестве домашней работы, ведь в видеозаписи подробно приводятся решения к различным заданиям. Помимо простого вывода решений, приводятся выноски и теоретические объяснения спокойным голосом диктора, текст которого составлен профессионалами.

Какие формулы с двумя аргументами школьники уже изучили? Это косинус, синус и тангенс суммы и разности аргументов х и у. Последнее было выведено из первых двух. Что же такое формула двойного аргумента? Аргумент умножен на 2. В некоторых случаях появляется заменить, например, sin2х через другую формулу для простоты решения. Как же быть?

Итак, как известно, 2х можно записать в виде суммы аргумента х с ним же, то есть х+х. Записав в такой форме, мы можем увидеть, что это формула синус суммы аргументов, вернее повторяющегося аргумента. А эта формула хорошо известна и изучена уже и на практике. Подставив новые значения в формулу, получаем новое правильно, по которому можно понять, как заменить синусу двойного аргумента.

Далее, аналогичным образом выводится формула двойного аргумента для косинуса. Показав первый пример получения формулы, можно предложить школьникам самостоятельно получить формулу косинуса суммы двойного аргумента.

Таким же способом в видеозаписи выводиться формула тангенса двойного аргумента. Приводится на экран результат. Подробно комментируется диктором.

Для того чтобы не зазубривать без понимания данные формулы, что часто делают некоторые ученики, которые знать необходимо, нужно попробовать самостоятельно их вывести. Таким образом, они запомнятся автоматически и с пониманием.

Далее видеоурок переходит в практическую часть. Примеры взяты такие, которые часто будут встречаться в домашних работах, самостоятельных или контрольных.

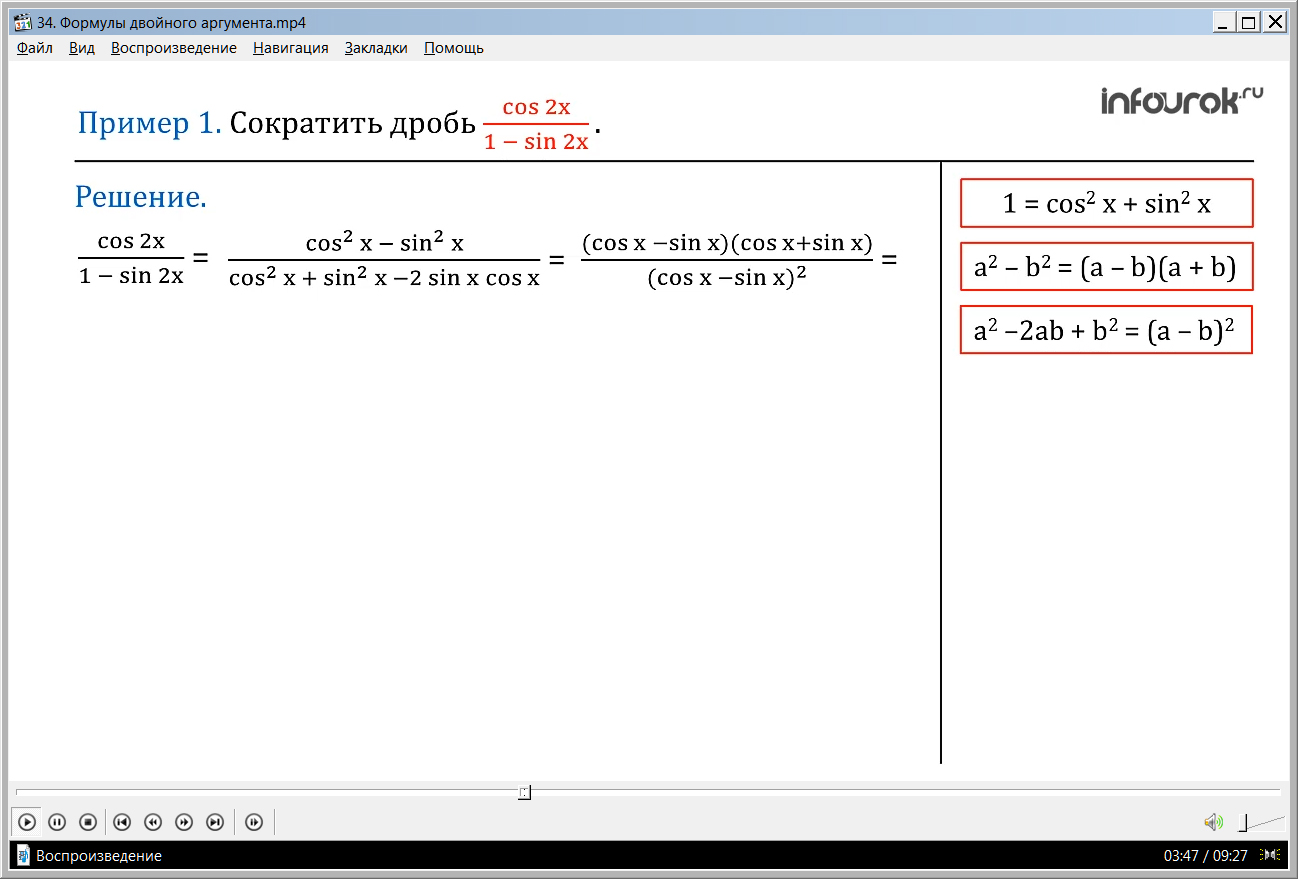
Первый пример предлагает сократить некоторую дробь. В числителе мы видим косинус двойного аргумента, с формулой которого мы столкнулись в данном уроке. Знаменатель же, представляет разность единицы от синуса двойного аргумента. Как известно, единиц можно заменить суммой квадрата косинуса и синуса. Это основное тригонометрическое утверждение, забыть которое нельзя ни в коем случае. Из него было выведено огромное количество различных формул и правил.

Заменив единицу в знаменателе, косинус и синус двойного аргумента изученными формулами, которые появляются с правой стороны решений, появляется возможность сократить дробь. Ответ выводится на экран.

Второй пример предлагает школьникам доказать некоторое заданное тождество. При этом используются также изученные формулы. Таким образом, школьники могут понять, как важно знать эти правила и научиться «видеть» при решении практических примеров. Доказательство само по себе достаточное объемное, однако, при помощи объяснений и комментированию диктора станут быстро понятными и очевидными. Школьники могут попробовать самостоятельно повторить доказательство. Это будет, однозначно, плюсом, поможет развить навыки математического мышления.

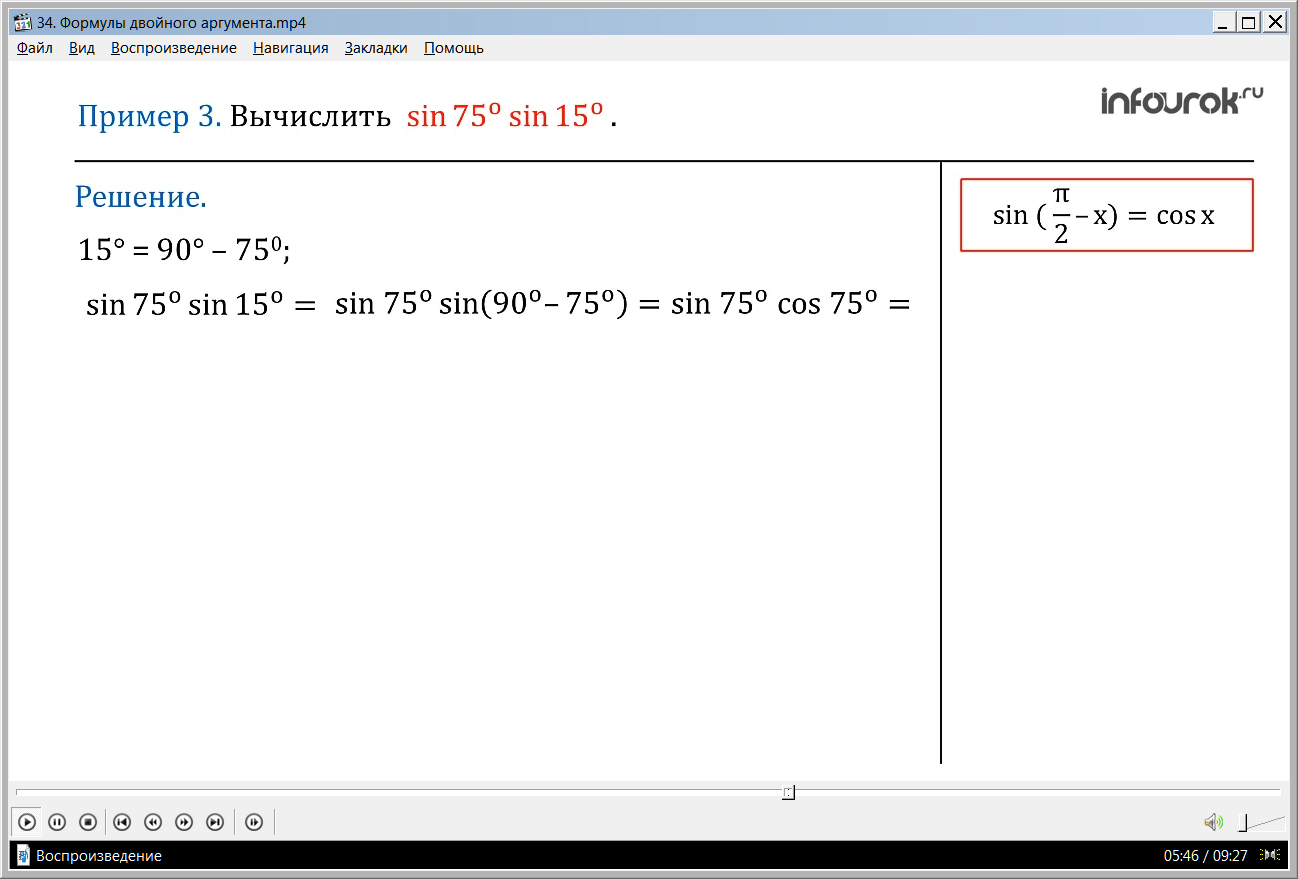
Третий пример предлагает попробовать найти решение для выражения с конкретными числовыми значениями – то есть определенными величинами градусов.

Так как заданные значения не являются табличными, рекомендуется заменить их в суммой или разностью табличных значений. А далее можно с легкостью воспользоваться формулами косинуса и синуса двойного аргумента и некоторыми ранее изученными формулами. Ответ выводится в конце данного решения. Подобные примеры будут еще часто встречаться школьникам.

Четвертый пример, уравнение, также важно понять. В тригонометрии достаточно часто будут встречаться уравнения, содержащие косинус, синус, тангенс и котангенс. То есть неизвестное будет являться аргументов данных тригонометрических функций.

Диктор предлагает привести уравнение к множителям, так как с правой стороны стоит 0. А, как известно, произведение будет равняться такой правой стороне лишь тогда, когда одно из них будет равно нулю. Так как множителей два, уравнение имеет два корня.

Эти подробные решения помогут начинающим учителям правильно и грамотно, пошагово объяснить школьникам практическую часть.

Формулы двойного аргумента

Формулы, позволяющие выразить sin 2x(синус два икс), cos 2x, tg 2x через

sinx, cosx, tgx, называют формулами двойного аргумента.

Выведем эти формулы. Представим 2х как сумму х + х и применим уже известные формулы синус суммы, косинус суммы и тангенс суммы,

sin(x + y) = sin x cos y + cos x sin y,

sin 2x = sin(х + х)= sinхcos x + cos x sinх = 2 sinхcos x,

Выведем формулу двойного аргумента tg 2x

тангенс два икс представим как тангенс суммы икс и икс, применим формулу тангенса суммы и получим в числителе сумма тангенс икс и тангенс икс, знаменатель разность единицы и произведения тангенс икс и тангенс икс, выполним действия и получим два тангенс икс деленное разность единицы и квадрата тангенса икс

Итак, sin2x =2 sinх cosx (синус двух икс равен удвоенному произведению синуса икс на косинус икс), эта формула справедлива для любого значения икс,

cos 2x= cos 2 х – sin 2 х (косинус двух икс равен разности квадратов косинуса и синуса), эта формула тоже справедлива для любого значения икс,

tg 2x = (тангенс двух икс равен частному двух тангенсов икс на разность единицы и квадрата тангенса икс), эта формула справедлива только для тех икс, для которых определены tgx и tg2x, а также знаменатель дроби не равен нулю.

Рассмотрим примеры применения формул двойного аргумента.

Решение. В числителе данной дроби применим формулу косинус двойного аргумента,

а в знаменателе – воспользуемся тем, что 1 = cos 2 х + sin 2 х, и применим формулу синуса двойного аргумента.

Тогда получим: в числителе разность квадратов косинуса и синуса, в знаменателе от суммы квадратов косинуса и синуса вычесть удвоенное произведение синуса икс на косинус икс.

(далее применим формулы сокращенного умножения: в числителе – разность квадратов а 2 – b 2 = (a – b)(a + b), а в знаменателе – «свернем» в квадрат разности а 2 –2ab + b 2 = (a – b) 2 )

( и после сокращения получим)

В числителе сумму косинуса икс и синуса икс, в знаменателе разность косинуса икс и синуса икс.

Рассмотрим левую часть тождества.

Зная, что тангенс икс – это отношение синуса икс к косинусу икс, преобразуем правую часть равенства, представив тангенс квадрат икс в виде частного синус квадрат икс на косинус квадрат икс:

( приведем к общему знаменателю и числитель, и знаменатель на экране показать дополнительные множители 1 и cos 2 x)

(воспользуемся тем, что cos 2 х + sin 2 х=1, и правилом деления дробей: первую дробь списываем вторую переворачиваем )

сократим н и получим

Значит cos2x= cos 2x., что и требовалось доказать

Чтобы привести к формуле двойного аргумента выражение умножим и разделим на два:

Таким образом в числителе – формула синуса двойного аргумента

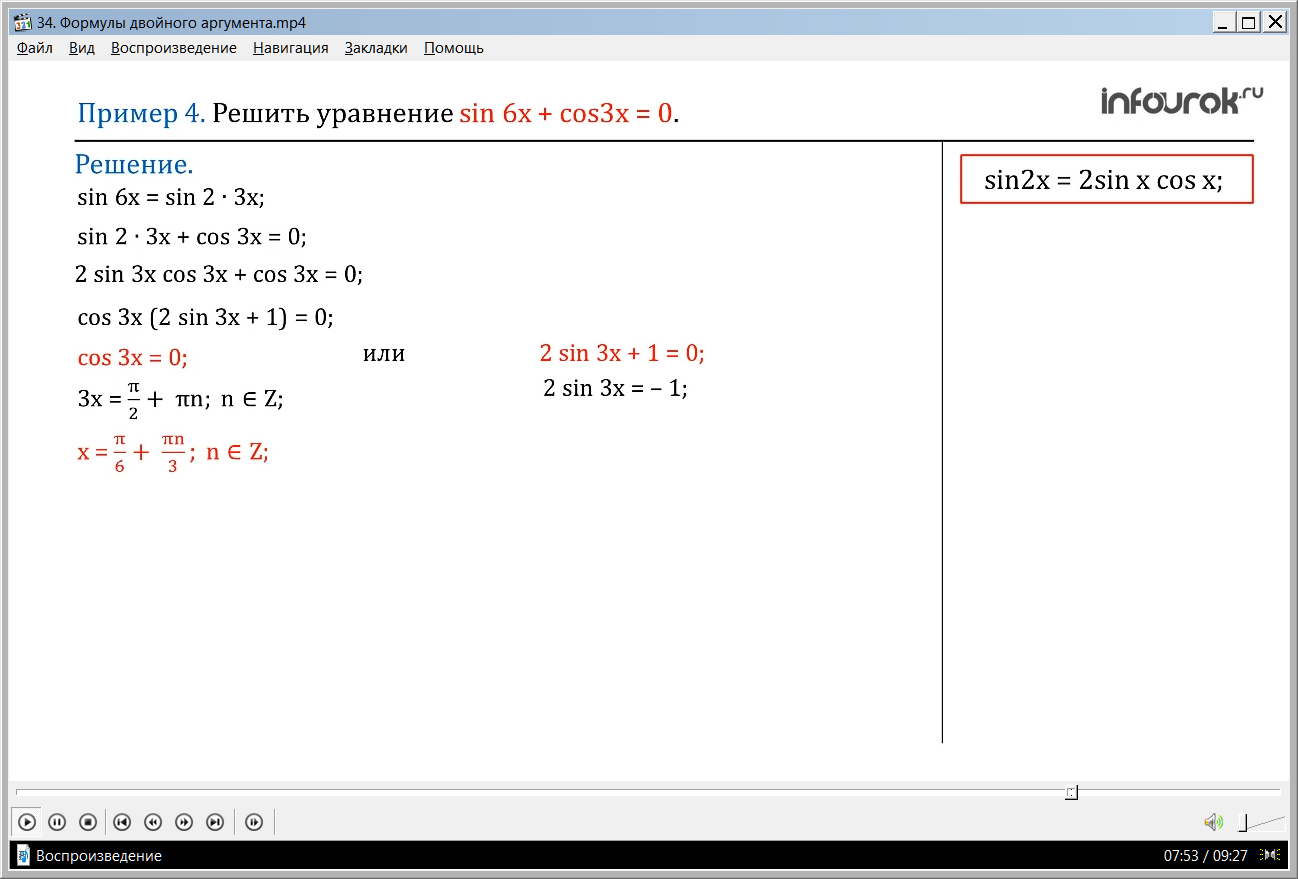
ПРИМЕР 4. Решить уравнение sin 6x + cos3x = 0.

Решение. В левой части уравнения к выражению sin 6x применим формулу синуса двойного аргументаsin2x = 2sinxcosx,

представим sin 6x= sin2∙3x

расписали синус 6х как синус двойного угла 3х

2sin 3x cos3 х+ cos3x =0

Выносим общий множитель cos3x за скобки

cos3x(2 sin3х + 1) = 0,

Получаем произведение косинус трех икс и суммы два синус трех икс и единицы. Так как произведение равно нулю, значит один из множителей равен нулю.

cos3x = 0 или 2 sin3х + 1 = 0.

Из уравнения cos3x = 0 находим:

Из уравнения 2 sin3х + 1 = 0, Переносим единицу в правую часть, находим:

Делим обе части уравнения на два:

3х = (- 1) n arcsin(–) + πn, ;

Так как arcsin(–)=–arcsin, тогда sin(– )= –

Заменим arcsin(- ) на –

Делим обе части на коэффициент перед икс получаем

© 2021 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Источник