Что такое формула включений и исключений

Формула включений и исключений

На этой странице мы собрали примеры решения учебных задач на применение принципа включений-исключений в комбинаторных задачах по теории вероятностей или дискретной математике.

Краткая теория

Формула включений и исключений для двух множеств

Формула включений и исключений для трех множеств

Разберем примеры решений типовых задач с этой формулой включений и исключений для случая 2 и 3 множеств (другие примеры подобных заданий вы найдете в разделе Примеры по дискретной математике: Множества и отношения).

Примеры решенных задач

Задача 1. Формула включений и исключений (для трех множеств). Известно, что свойством А обладает n объектов, В — m объектов, С — с объектов, АВ — р объектов, АС — g объектов, ВС — r объектов, АВС — q объектов. Сколько всего объектов?

Задача 2. Из 100 человек студентов, сдавших сессию, 48 человек сдали экономику, 42 студента – математику и 37 человек – логику. По экономике или математике сдали экзамен 76 человек, по экономике или логике также 76 человек, а по математике или логике – 66 человек. Сколько человек сдали хотя бы один экзамен, если все три предмета сдали 5 человек? Сколько человек не сдали ни одного экзамена? Сколько человек сдали только один экзамен по логике?

Задача 5. Из 100 туристов, выехавших в заграничное путешествие, 10 человек не знают ни немецкого, ни французского языков, 76 человек знают немецкий и 83 – французский. Сколько туристов знают оба эти языка?

Задача 6. В отряде из 40 ребят 30 умеют плавать; 27 умеют играть в шахматы; 5 не умеют ни плавать, ни играть в шахматы. Определить количество ребят, умеющих плавать и играть в шахматы.

Видеоурок: Формула включений и исключений

Решебник по терверу и комбинаторике

Если решения нужны срочно и почти даром? Ищите в решебнике по теории вероятностей:

Источник

Формула включения-исключения

Содержание

Формула включения-исключения [ править ]

Для случая из двух множеств [math] A, B [/math] формула включения-исключения имеет следующий вид:

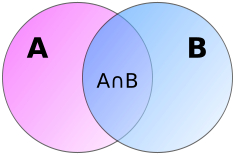
В силу того, что в сумме [math] | A | + | B |[/math] элементы пересечения [math] A \cap B [/math] учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера—Венна для двух множеств, приведенной на рисунке справа.

Для случая с большим количеством рассматриваемых множеств [math] n [/math] процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы.

Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств.

Приведем два разноплановых доказательства теоремы.

I. Комбинаторное доказательство теоремы.

Докажем, что [math] \sum \limits_^(-1)^j= 0[/math]

II. Доказательство теоремы по индукции.

l[/math] — это количество множеств, мощность пересечения которых мы ищем. Для случая [math]

l=1[/math] равенство обращается в тривиальное ( [math] |A| = |A_1| [/math] — истинно). Для случая [math]

l=2[/math] справедливость теоремы пояснена выше. Таким образом, [math]

l=2[/math] — база индукции.

Предположим, что для [math]

l=n-1[/math] равенство верно. Докажем, что равенство истинно для [math]

Пусть [math] A [/math] — объединение [math]

Исходя из предположения индукции, имеем, что [math] | B | = \sum \limits_> (-1)^ <|I|+1>\left| \bigcap \limits_ < j \in I>A_j \right| [/math]

Кроме того, так как формула верна для [math]

Очевидно, что [math] B \cap A_n = \left( \bigcup \limits_^A_i \right) \cap A_n = \bigcup \limits_^ \left( A_i \cap A_n \right) (**)[/math]

Опираясь на предположение индукции и равенство [math] (**) [/math] имеем, что [math] |B \cap A_n| = \sum \limits_> (-1)^ <|I|+1>\left| \bigcap \limits_ < j \in I>\left( A_j \cap A_n \right) \right| = \sum \limits_> (-1)^ <|I|+1>\left| \bigcap \limits_ < j\in I \cup \< n \>> A_j \right| [/math]

Подставим полученные значения в [math](*)[/math] :

Докажем, что [math] | A_n |+\left( \sum \limits_> (-1)^ <|I|+1>\left| \bigcap \limits_ < j \in I >A_j \right| \right) + \left( \sum \limits_> (-1)^ <|I|+2>\left| \bigcap \limits_ < j\in I \cup \< n \>> A_j \right| \right) [/math] [math] = \sum \limits_ (-1)^ <|I|+1>\left| \bigcap \limits_ < j \in I >A_j \right| [/math]

Равенство справедливо, потому что все наборы [math] I \in 2^N [/math] можно разбить на две группы :

Таким образом, для [math]

l=n[/math] мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана.[math]\triangleleft[/math]

Беспорядки [ править ]

Явная формула с использованием принципа включения-исключения [ править ]

Подставляя соответствующие значения мощностей множеств в формулу включения-исключения, получаем:

Рекурретное соотношение для нахождения количества беспорядков [ править ]

1) Докажем второе соотношение:

2) Докажем первое соотношение:

У нас есть [math] n [/math] чисел и столько же мест. Мы должны найти количество способов разместить эти числа так, что ни одно из чисел не оказалось на месте с таким же номером.

В итоге получается необходимая формула.[math]\triangleleft[/math]

Задача о перестановках [ править ]

Посчитаем количество «плохих» перестановок, то есть таких, у которых первый элемент [math] \leqslant 1 [/math] (множество таких перестановок обозначим [math] X [/math] ) и/или последний [math] \leqslant 8 [/math] (множество таких перестановок обозначим [math] Y [/math] ).

Тогда количество «плохих» перестановок по формуле включений-исключений равно:

[math] |X|+|Y|-|X \cap Y| [/math]

Проведя несложные комбинаторные вычисления, получим:

Задача о нахождении числа взаимно простых четвёрок [ править ]

Воспользуемся формулой включений-исключений, суммируя количество четвёрок, делящихся на [math] d [/math] (но, возможно, делящихся и на больший делитель).

Таким образом, с помощью формулы включений-исключений мы суммируем количество четвёрок, делящихся на простые числа, затем отнимаем число четвёрок, делящихся на произведение двух простых, прибавляем четвёрки, делящиеся на три простых, и т.д.

Источник

Формула включений и исключений.

Пусть |Ω| — общее количество объектов, а |A_i| — количество объектов, которые обладают свойством i, |A 1∩ A 2 | — количество объектов, обладающих свойствами 1 и 2,…,|A₁∩…∩A_n| — количество объектов, обладающих свойствами 1,…,n. Тогда количество объектов, не обладающих ни одним из свойств равно:

Примеры решения задач

В летнем лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

Решение:

Ответ: 10 ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

Сколько существует натуральных чисел, не превосходящих 1000, которые не делятся ни на 3, ни на 5?

Решение:

Натуральное число, которое делится на 3 можно представить в виде: 3·n, где n — натуральное число. Следовательно, 333 числа делятся на 3.

Натуральное число, которое делится на 5 можно представить в виде: 5·n, где n — натуральное число. Следовательно, 200 чисел делятся на 5.

Натуральное число, которое делится и на 3 и на 5 можно представить в виде: 15·n, где n — натуральное число. Следовательно, 66 чисел делятся на и на 3 и на 5.

Ответ: 533 числа не делятся ни на 3, ни на 5.

Сколько существует натуральных чисел, не превосходящих 1000, которые не делятся ни на 5, ни на 7?

Решение:

Натуральных чисел, которые делятся на 5: 200.

Натуральных чисел, которые делятся на 7: 142.

Числа, которые делятся и на 5 и на 7: 28.

Ответ: 686 чисел, не превосходящих 1000, не делятся ни на 5, ни на 7.

Каждая сторона в треугольнике ABC разделена на 8 равных отрезков. Сколько существует различных треугольников с вершинами в точках деления (точки A, B, C не могут быть вершинами треугольников), у которых ни одна сторона не параллельна ни одной из сторон треугольника ABC?

Решение:

На каждой стороне треугольника 7 точек. Всего можно построить 7 3 треугольников. У 3·7 2 треугольников одна из сторон параллельна одной из сторон треугольника ABC, у 3·7 треугольников – две стороны, у 1 треугольника – все стороны.

Ответ: 216 треугольников.

В классе 30 учеников. Сколькими способами они могут пересесть так, чтобы ни один не сел на своё место?

Решение:

Общее количество пересаживаний равно: 30!.

30!-29!30+28!·30·29/2!-…-30+1=30!(1-1/1!+1/2!-…-1/29!+1/30!)=30!(1/2!-…-1/29!+1/30!).

Ответ: 30!(1/2!-…-1/29!+1/30!).

Источник

Формула включений и исключений

Пусть задано конечное множество А. Число его элементов обозначим n(А). Найдем сколько элементов содержится в множестве А ∪ В. Основная формула нахождения числа элементов суммы двух множеств

n(А ∪ В) = n(А) + n(В) – n(А ∩ В) (1)

Действительно, n(А ∪ В) — это сумма числа элементов множеств А и В, но при подсчете элементы, принадлежащие А ∩ В учитывались дважды. С помощью формулы (1) можно получить формулы для определения числа элементов суммы любого числа множеств. Например,

n(А ∪ В ∪ С) = n(А ∪ (В ∪ С)) = n(А) + n(В ∪ С) – n(А ∩ (В ∪ С)) =

= n(А) + n(В) + n(С) – n(В ∩ С) – n((А ∩ В) ∪ (А ∩ С)) =

= n(А) + n(В) + n(С) – n(В ∩ С) – (n(А ∩ В) + n(А ∩ С) – n((А ∩ В) ∩ (А ∩ С))) =

=n(А) + n(В) + n(С) – n(В ∩ С) – n(А ∩ В) – n(А ∩ C) + n(А ∩ В ∩ С).

n(А ∪ В ∪ С) = n(А) + n(В) + n(С) – n(А ∩ В) – n(В ∩ С) – n(А ∩ C) + n(А ∩ В ∩ С) (2)

Примеры с подробным решением.

Задача 1. Из 100 школьников английский знают 42, немецкий — 30, французский — 28, английский и немецкий — 5, английский и французский — 10, немецкий и французский — 8, английский, немецкий и французский — 3 школьника. Сколько школьников не знают ни одного языка?

Обозначим через А — множество школьников, знающих английский язык; N — множество школьников, знающих немецкий язык; F — множество школьников, знающих французский язык.

Тогда n(A) = 42, n(N) = 30, n(F) = 28, n(A ∩ N) = 5,

n(A ∩ F) = 10, n(N ∩ F) = 8, n(A ∩ N ∩ F) = 3.

Найдем с помощью формулы включений и исключений количество школьников, знающих хотя бы один из перечисленных иностранных языков.

n(A ∪ N ∪ F) = n(A) + n(N) + n(F) =

= n(A ∩ N) – n(A ∩ F) – n(N ∩ F) + n(A ∩ N ∩ F) =

= 42 + 30 + 28 – 5 – 10 – 8 + 3 = 80.

Следовательно, не знают ни одного иностранного языка:

100 – 80 = 20 школьников.

Эту же задачу можно решить с помощью диаграммы Эйлера–Венна (рис. 1).

Так как 3 языка знают 3 школьника, то английский и немецкий знают 5 – 3 = 2, английский и французский — 10 – 3 = 7,

немецкий и французский — 8 – 3 = 5 школьников.

Только английский знают 42 –(2 + 3 + 7) = 30,

только немецкий — 30 – (2 + 3 + 5) = 20,

только французский — 28 – (3 + 5 + 7) = 13 школьников.

Ни одного языка не знают 100 – (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20 школьников.

Задача 2. Сколько двузначных чисел не делятся ни на 2, ни на 3, ни на 5, ни на 11?

Решение. Обозначим: А — множество двузначных чисел, делящихся на 2;

В — множество двузначных чисел, делящихся на 3;

С — множество двузначных чисел, делящихся на 5;

D — множество двузначных чисел, делящихся на 11.

n(A ∪ B ∪ C ∪ D) — количество двузначных чисел, делящихся хотя бы на одно из чисел 2; 3; 5; 11.

n(A ∪ B ∪ C ∪ D) = n(A) + n(B) + n(C) + n(D) –

– n(A ∩ B) – n(A ∩ C) – n(A ∩ D) – n(B ∩ C) –

– n(B ∩ D) – n(C ∩ D) + n(A ∩ B ∩ C) + n(A ∩ B ∩ D) +

+ n(A ∩ C ∩ D) + n(B ∩ C ∩ D) – n(A ∩ B ∩ C ∩ D).

n(A) = 45, n(B) = 30, n(C) = 18, n(D) = 9,

n(A ∩ B) = 15, n(A ∩ C) = 9, n(A ∩ D) = 4, n(B ∩ C) = 6,

n(B ∩ D) = 3, n(C ∩ D) = 1, n(A ∩ B ∩ C) = 3,

n(A ∩ B ∩ D) = 1, n(A ∩ C ∩ D) = n(B ∩ C ∩ D) = n(A ∩ B ∩ C ∩ D) = 0.

Итак, n(A ∪ B ∪ C ∪ D) = 45 + 30 +18 + 9 – 15 – 9 – 4 – 6 – 3 – 1 + 3 + 1 = 68.

Так как всего 90 двузначных чисел, то чисел, не делящихся ни на одно из заданных чисел:

Решение. Пусть A —множество учеников, которые увлекаются спортом,

Тогда |A| = 32, |B| = 21, |C| = 23, |A ∩ B| = 8, |A ∩ C| = 12, |B ∩ C| =4 |A ∩ B ∩ C| = 3

|(A ∩ B) ∪ ( B ∩ C) | = |A ∩ B| + |B ∩ C| − |A ∩ B ∩ C| = 8 + 4 – 3 = 9

Тогда, только программированием занимается 21 – 9 = 12 учеников.

|(A ∩ C) ∪ ( B ∩ C) | = |A ∩ C| + |B ∩ C| − |A ∩ B ∩ C| = 12 + 4 – 3 = 13

Тогда, только математикой занимается 23 – 13 = 10 учеников.

По формуле включений и исключений для трёх множеств находим число учеников увлекающихся спортом, программированием или математикой:

|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |A ∩ C| − |B ∩ C| + |A ∩ B∩ C| = =32+21+23-8-12-4+3 = 55

Значит, ничем не увлекается 70 − 55 = 15 человек. Ответ: 15.

1. В спортивном классе обучаются 24 человека. Каждый учащийся занимается хотя бы одним видом спорта (баскетболом или волейболом), из них баскетболом и волейболом занимаются 12 человек. Сколько человек занимается только волейболом, если их в 3 раза больше, чем тех, кто занимается только баскетболом?

2. В одном украинском городе все жители говорят на русском или украинском языке. По-украински говорят 80 % всех жителей, а по-русски — 75 %. Сколько процентов всех жителей говорят на обоих языках?

3. Группа ребят отправилась в поход. Семеро из них взяли с собой бутерброды, шестеро — фрукты, пятеро — печенье. Четве- ро ребят взяли с собой бутерброды и фрукты, трое — бутерброды и печенье, двое — фрукты и печенье, а один — и бутерброды, и фрукты, и печенье. Сколько ребят пошли в поход?

4. Староста класса, в котором 40 человек, подводил итоги по успеваемости группы за I полугодие. Получилась следующая картина: из 40 учащихся не имеют троек по русскому языку 25 человек, по математике — 28 человек, по русскому языку и мате- матике — 16 человек, по физике — 31 человек, по физике и ма- тематике — 22 человека, по физике и русскому языку 16 человек. Кроме того, 12 человек учатся без троек по всем трем предметам. Классный руководитель, просмотрев результаты, сказал: «В тво- их расчетах есть ошибка». Составьте диаграмму Эйлера–Венна и объясните, почему это так.

5. В лаборатории института работают несколько человек. Каждый из них знает хотя бы один иностранный язык. 7 человек знают английский, 7 — немецкий, 8 — французский, 5 знают английский и немецкий, 4 — немецкий и французский, 3 — французский и английский, 2 человека знают все три языка. Сколько человек работает в лаборатории? Сколько из них знает только французский язык? Сколько человек знает ровно 1 язык?

6. Сколько целых чисел от 0 до 999 не делятся ни на 5, ни на 7, ни на 11?

Ответы: 1. 9. 2. 55 %. 3. 10. 4. Если на диаграмме Эйлера– Венна отметить данные в непересекающихся множествах класса, то общее число учащихся класса получится равным 42, а не 40, как сказано в условии. 5. 12; 3; 4. 6. 376.

Источник

15. Формула включений и исключений

Принцип сложения можно применять в тех случаях, когда все множество перечисляемых комбинаций разбивается на попарно непересекающиеся группы комбинаций. Обобщим принцип сложения на случай, когда могут иметь место случаи непустых пересечений.

Пусть имеется n предметов, которые могут обладать двумя свойствами A и B. При этом каждый предмет может либо не обладать ни одним из этих свойств, либо обладать одним или обоими свойствами. Обозначим через n(A), n(B), n(AB) количество предметов, обладающих свойством A, свойством B, обоими свойствами. Тогда число предметов, обладающих хотя бы одним из указанных свойств, равно

. (13.1)

Появление третьего слагаемого связано с тем, что число предметов обладающих обоими свойствами при сложении n(A) и n(B) учитывались дважды (см. рис. 13.1).

Формула (13.1) является частным случаем более общей формулы:

(13.2)

Которую называют формулой перекрытий, или формулой включений и исключений. Чаще эту формулу записывают в следующем виде.

Обозначим символом 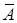свойство A, которым данные предметы не обладают. Тогда число предметов, не обладающих ни одним из указанных свойств, будет равно

(13.3)

Здесь алгебраическая сумма распространена на все комбинации свойств A1,…,Am (без учета их порядка), причем знак «+» ставится, если число учитываемых свойств четно, и знак «–», если это число нечетно. Название формулы (13.2) как формулы включений и исключений связано с тем, что сначала исключаются все предметы, обладающие хотя бы одним из свойств, потом включаются предметы, обладающие по крайней мере двумя из этих свойств, после этого исключаются предметы, обладающие по крайней мере тремя свойствами, и т. д.

В случае трёх свойств формулы (13.2) и (13.3) примут вид:

, (13.4)

. (13.5)

Пример 13.1. В научно-исследовательском институте работают 67 человек. Из них 47 знают английский язык, 35 – немецкий язык и 23 – оба языка. Сколько человек в институте не знают ни английского, ни немецкого языков?

Решение. Обозначим через A – сотрудников, знающих английский язык, через B – сотрудников, знающих немецкий язык. По условию

.

Итак, 8 человек не знают ни английского, ни немецкого языка.

Пример 13.2. Сколько можно сделать перестановок из n элементов, в которых данные два элемента a и b не стоят рядом? Данные три элемента a, b, c не стоят рядом (в любом порядке)? Никакие два из элементов a, b, c не стоят рядом?

Решение. Если a и b стоят рядом, то их можно объединить в один знак. Учитывая, что a и b можно переставлять местами, получаем перестановок, в которых a и b стоят рядом. Тогда в

Случаях они не стоят рядом. Точно также получаем, что a, b, c не стоят рядом

Случаях. Никакие два из элементов a, b, c не стоят рядом

Случаях (формула включений и исключений).

Пример 13.3. Сколькими способами можно посадить рядом 3 англичан, 3 французов и 3 немцев так, чтобы никакие три соотечественника не сидели рядом?

Решение. 9 человек можно пересаживать 9! способами. Найдём, во скольких перестановках 3 англичанина сидят рядом. Все такие перестановки получаются из одной пересаживанием между собой англичан (3! способов) и 3 французов и 3 немцев и компании из трех англичан (7! способов). Всего получаем 3!7! перестановок. Во стольких же перестановках сидят рядом 3 французов и во стольких же – 3 немцев. Далее, в (3!)25! перестановках сидят рядом трое англичан и трое французов, а также трое англичан и трое немцев, трое французов и трое немцев. И, последнее, в (3!)4 перестановках сидят рядом и англичане, и французы, и немцы. В результате, по формуле включений и исключений, находим

способа.

13.1. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек, с ветчиной – 42 человека, и с сыром и с колбасой – 28 человек, и с колбасой и с ветчиной – 31 человек, и с сыром и с ветчиной – 26 человек. Все три вида бутербродов взяли 25 человек, а несколько человек вместо бутербродов захватили с собой пирожки. Сколько человек взяли с собой пирожки?

13.2. В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык, 6 человек знает английский язык, 6 – немецкий, 7 – французский, 4 знают английский и немецкий, 3 – немецкий и французский, 2 – французский и английский, 1 человек знает все три языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Сколько человек знают только один язык?

Ответ: По формуле включений и исключений число работающих равно 6+7+6–4–3–2+1=11. Только английский знают 6–4–2+1=1, только немецкий 6–4–3+1=0, только французский 7–3–2+1=3. Т. о., только один язык знают 4 человека.

13.3. Староста одного класса дал следующие сведения об учениках: «В классе учатся 45 школьников, в том числе 25 мальчиков. 30 школьников учатся на хорошо и отлично, в том числе 16 мальчиков. Спортом занимаются 28 учеников, в том числе 18 мальчиков и 17 школьников, учащихся на хорошо и отлично. 15 мальчиков учатся на хорошо и отлично и занимаются спортом». Покажите, что в этих сведениях есть ошибка.

Ответ: Число школьников, которые не учатся на хорошо и отлично и не занимаются спортом, равно 45–30–28+17=4. Число мальчиков, которые не учатся на хорошо и отлично и не занимаются спортом, равно 25–16–18+15=6, т. е. их больше 4, что не может быть.

13.4. В лифт сели 8 человек. Сколькими способами они могут выйти на четырех этажах так, чтобы на каждом этаже вышел, по крайней мере, один человек?

Ответ: 8 пассажиров могут распределиться между этажами 48 способами. Из них в 38 случаях на данном этаже, 28 случаях на данных двух этажах и в 1 случае на данных трех этажах не выйдет ни один человек. По формуле включений и исключений получаем способа.

13.5. Сколько неотрицательных целых чисел, меньших чем миллион, содержит все цифры 1, 2, 3, 4? Сколько чисел состоит только из этих цифр?

Ответ: По формуле включений и исключений получаем, что все цифры 1, 2, 3, 4 содержат чисел. Только из цифр 1, 2, 3, 4 состоят чисел.

Источник