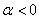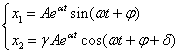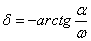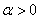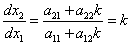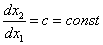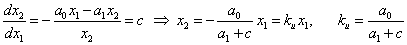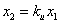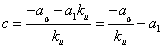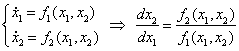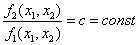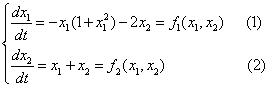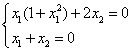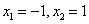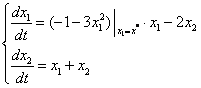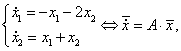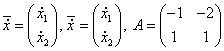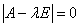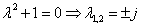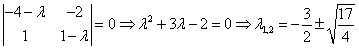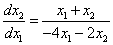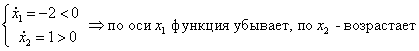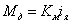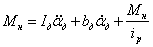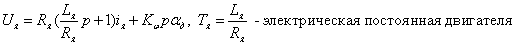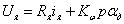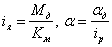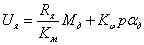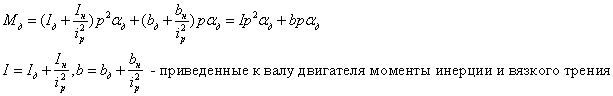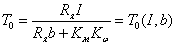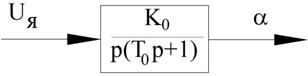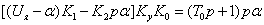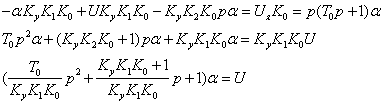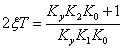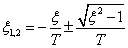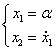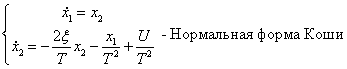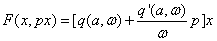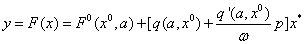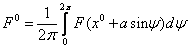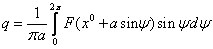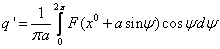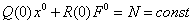Что такое фазовый портрет

Julia и фазовые портреты динамических систем

Продолжаем осваивать молодой и перспективный язык общего назначения Julia. Но для начала нам нужна как раз таки сугубо узкая возможность применения — для решения типичных задач физики. Это самая удобная тактика освоения инструмента: чтоб набить руку, будем решать насущные проблемы, постепенно увеличивая сложность и находя способы облегчения своей жизни. Короче, будем решать дифуры и строить графики.

Для начала качаем графический пакет Gadfly, да сразу полную версию разработчика, чтоб хорошо работала с нашей Julia 1.0.1. Вбиваем в нашем REPL, JUNO или Jupyter notebook:

Не самый удобный вариант, но пока ждём обновления PlotlyJS можно ради сравнения и попробовать.

Также нужен могущественнейший инструмент для решения дифференциальных уравнений DifferentialEquations

Это самый обширный и поддерживаемый пакет, предоставляющий уйму методов решения дифуров. Теперь приступим к фазовым портретам.

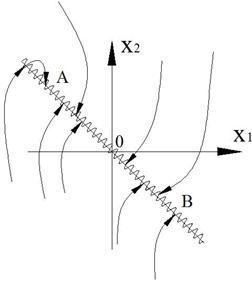
Решения обыкновенных дифференциальных уравнений часто удобнее изображать не в привычном виде , а в фазовом пространстве, по осям которого откладываются значения каждой из найденных функций. При этом аргумент t входит в графики лишь параметрически. В случае двух ОДУ такой график – фазовый портрет системы, является кривой на фазовой плоскости и поэтому особенно нагляден.

Осциллятор

Динамика гармонического осциллятора с затуханием описывается следующей системой уравнений:

и независимо от начальных условий (х0, у0), приходит в состояние равновесия, точку (0,0) с нулевым углом отклонения и нулевой скоростью.

При решение принимает вид свойственный для классического осциллятора.

Разберем код. Функция принимает значения частоты и параметра затухания, а также начальные условия. Вложенная функция syst() задает систему. Для того чтоб вышло однострочно воспользовались матричным умножением. Функция solve() принимая огромное количество параметров весьма гибко настраивается для решения проблемы, но мы лишь указали метод решения — Рунге-Кутты 4 (есть ещё много других), относительную погрешность, и то, что надо сохранять не все точки, а только каждую четвертую. В переменную sol сохраняется матрица-ответ, причем, sol.t содержит вектор значений времен, а sol.u решения системы на этих временах. Все это спокойно рисуется в Plots, а для Gadfly придется укомплектовывать ответ в матрицу поудобней. Времена нам не нужны, так что возвращаем только решения.

Построим фазовый портрет:

Теперь рассмотрим не малые колебания, а колебания произвольной амплитуды:

График решения на фазовой плоскости не является эллипсом (что говорит о нелинейности осциллятора). Чем меньше мы будем выбирать амплитуду колебаний (т.е. начальные условия), тем меньше будет проявляться нелинейность (поэтому-то малые колебания маятника можно считать гармоническими).

Брюсселятор

Эта модель описывает некоторую автокаталитическую химическую реакцию, в которой определенную роль играет диффузия. Модель была предложена в 1968 г. Лефевром и Пригожиным

Неизвестные функции отражают динамику концентрации промежуточных продуктов химической реакции. Параметр модели имеет смысл исходной концентрации катализатора (третьего вещества).

Более детально, эволюцию фазового портрета брюсселятора можно наблюдать, проводя расчеты с различным параметром . При его увеличении узел будет сначала постепенно смещаться в точку с координатами (1, ), пока не достигнет бифуркационного значения =2. В этой точке происходит качественная перестройка портрета, выражающаяся в рождении предельного цикла. При дальнейшем увеличении происходит лишь количественное изменение параметров этого цикла.

На сегодня достаточно. В следующий раз попробуем научиться пользоваться другим графическим пакетом на новых задачах, попутно набивая руку на синтаксис Юлии. В процессе решения задач потихоньку начинают прослеживаться не то чтобы прям плюсы и минусы… скорее приятности и неудобства — этому следует посвятить отдельный разговор. И конечно хотелось бы на хабре увидеть что-то посерьезней моих игр с функциями — посему призываю джулистов поопытней рассказать о более менее серьезных проектах, это помогло бы многим и мне в частности, в изучении этого замечательного языка.

Источник

Фазовые портреты «на пальцах» или что можно узнать о решениях диффура, не решая его

Очень часто в ряде наук встречается ситуация, когда модель рассматриваемого процесса сводится к дифференциальному уравнению. Причём, в большинстве реальных задач это уравнение довольно сложно решить, или совсем невозможно. И вот тут в полный голос звучит извечный вопрос: как быть?

Встречайте: фазовые портреты (они же фазовые диаграммы). Простым языком, фазовый портрет — это то, как величины, описывающие состояние системы (a.k.a. динамические переменные), зависят друг от друга. В случае механического движения это координата и скорость, в электричестве это заряд и ток, в известной популяционной задаче это количество хищников и жертв и т.д.

Чем хороши фазовые портреты? А тем, что их можно построить не решая динамические уравнения системы. В некоторых случаях построение фазового портрета становится совсем простой задачей. Однако, одновременно с этим, фазовые портреты дают вдумчивому наблюдателю очень много информации о поведении системы.

Начнём с простого примера — малых колебаний (так же называемых гармоническими). Малые колебания встречаются почти в каждой сфере естественных наук. Для определённости, будем рассматривать колебания металлического стержня, подвешенного за один из концов (частный случай так называемого физического маятника). Можно показать, что его колебания описываются следующим дифференциальным уравнением:

Где x — угол отклонения стержня от вертикали, точка над x означает производную по времени, а коэффициент перед синусом зависит от размера и массы стержня.

Если амплитуда (размах) колебаний достаточно мала, синус можно приближенно заменить его аргументом (вы ведь помните первый замечательный предел, нет?). В таком случае, уравнение принимает следующий вид:

Это уравнение легко решается регулярными методами, но, давайте, попробуем применить к нему метод фазовых портретов. Для этого, домножим уравнение на производную и проинтегрируем его один раз по времени:

Получилось выражение, первый член которого выглядит как кинетическая энергия. Это не случайно — на самом деле мы получили именно закон сохранения энергии. Постоянная Е в правой части (полная энергия системы на единицу массы) может принимать различные значения, которые соответствуют разным начальным состояниям системы.

Полученный нами закон сохранения превратился в уравнение кривой на плоскости (x,u):

Для разных значений Е мы получим разные кривые. Нарисуем несколько таких линий для разных значений энергии:

По горизонтальной оси отложена величина x, по вертикальной — u

Каждая из полученных линий называется фазовой траекторией. Когда меняется состояние системы, изображающая её точка движется по одной из этих траекторий, стрелки указывают направление движения изображающей точки.

По графику видно, что значения скорости и координаты меняются циклическим образом, то есть периодически повторяются. Отсюда можно сделать вывод, что описываемая рассмотренным уравнением система будет совершать колебания. Бинго! Именно так ведёт себя маятник, и если решить уравнение, решение будет иметь вид периодических функций (а именно — комбинации синуса и косинуса).

Теперь, поскольку нам понятна суть, можно перейти к чему-то посложнее. Выше мы очень сильно упростили уравнение и при этом ограничили себя только малыми колебаниями. Математик бы сказал, что мы линеаризовали уравнение и пренебрегли нелинейными эффектами. Так давайте включим в рассмотрение нелинейность. Вернёмся к самому первому уравнению — с синусом. Если мы повторим с ним то, что проделали с линейным уравнением, мы получим следующий закон сохранения:

В зависимости от значения энергии, мы опять получаем разные кривые, которые приведены на следующем рисунке, причем выбраны те же значения энергии, что и на первой диаграмме, и те же цвета для линий.

По горизонтальной оси отложена величина x, по вертикальной — u

Как видите, процессы происходящее в системе стали более разнообразными:

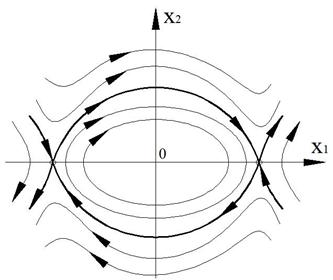
При малых энергиях (оранжевая и синяя траектории) существует колебательный режим, но колебания уже не являются гармоническими — фазовые траектории уже не имеют форму эллипсов.

При больших энергиях (зеленая траектория) колебаний уже нет, вместо этого мы получаем вращательное движение с переменной скоростью. И действительно, если достаточно сильно «толкнуть» стержень, он будет вращаться, замедляясь при подъёме и ускоряясь при спуске.

При определенном промежуточном значении энергии получается особый набор траекторий, которые отделяют друг от друга области соответствующие разным типам движения и поэтому называются сепаратрисами. И да, значение энергии для красной кривой было выбрано мной именно так, чтобы в нелинейном случае получилась сепаратриса. Каждая ветвь сепаратрисы это траектория, соответствующая особому типу движения. Посмотрим на диаграмму: движение начинается с очень маленькой скоростью от одного крайнего положения стержня, при приближении к положению равновесия скорость растёт, а после изображающая точка все более замедляясь уходит к крайнему положению, где и останавливается. Это соответствует тому, что мы поднимаем стержень вертикально вверх и отпускаем его, проносясь через положение равновесия он поднимается к верхней точке с другой стороны и останавливается.

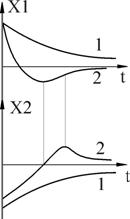
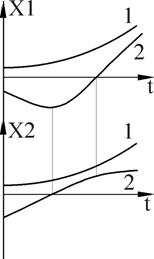
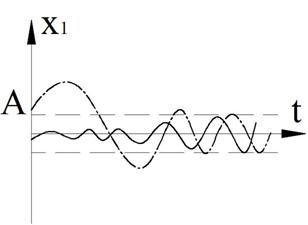
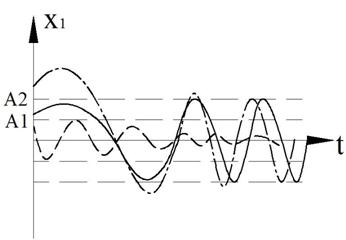
А теперь давайте посмотрим насколько близки к истине наши выводы, сделанные на основе фазовых портретов. Перед вами график решения линейного уравнения:

По горизонтальной оси отложено время, по вертикальной — x

По горизонтальной оси отложено время, по вертикальной — x

Цветовая маркировка на этих графиках такая же, как и на фазовых портретах. Судить о том, насколько верные выводы были сделаны на основе фазовых портретов я предоставлю вам, дорогие читатели. Обращу ваше внимание только на один момент — колебания в линейном случае происходят синхронно — с одной и той же частотой. В нелинейном же случае, частота колебания с большей амплитудой (синяя линия) оказывается меньше, чем у колебания с малой амплитудой (оранжевая линия). Это служит еще одним подтверждением того, что нелинейные колебания не являются гармоническими.

Ну и напоследок: это всего лишь поверхностный экскурс в метод фазовых портретов, и словосочетание «на пальцах» попало в заголовок неспроста. Те же, кто решит углубиться в перипетии данного предмета, увидят, что за фазовыми портретами скрывается намного большее.

Источник

2. ,

, , ,

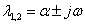
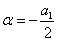
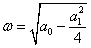
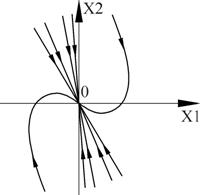
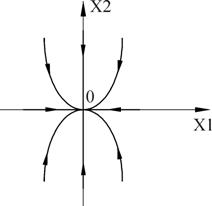
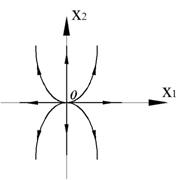
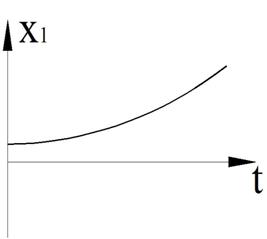
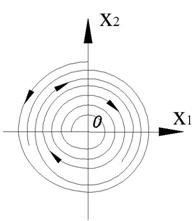
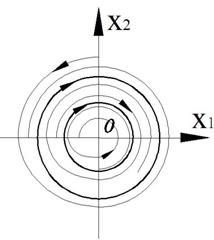
Рисунок 19 – Фазовый портрет и переходный процесс

Фазовый портрет представляет собой логарифмическую спираль, сходящуюся к нулю.

Точка (0,0) – особая точка типа «устойчивый фокус».

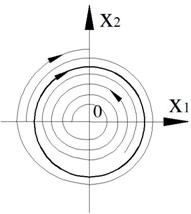
3. ,

, , ,

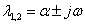
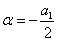
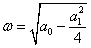
Фазовый портрет представляет собой логарифмическую спираль, рассходящуюся от нулю.

Точка (0,0) – особая точка типа «неустойчивый фокус».

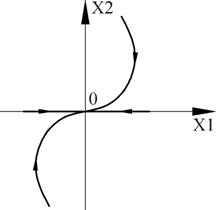
4. ,

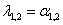
Рисунок 21 – Фазовый портрет

Рисунок 22 – Переходные процессы

Асимптоты: ,

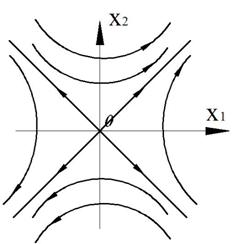
Точка (0,0) – особая точка типа «устойчивый узел».

Вырожденный случай получаем, когда корни одинаковы.

Если матрица в уравнении Коши имеет диагональный вид, то фазовый портрет имеет вид

Рисунок 24 – Частный случай фазового портрета системы

Если матрица имеет диагональный вид и корни равны, то имеем случай

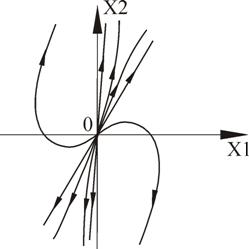
5. ,

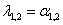
Рисунок 26 – Фазовый портрет

Рисунок 27 – Переходный процесс

Вырожденный случай получаем, когда корни одинаковы.

Рисунок 28 – Вырожденный неустойчивый узел

Если матрица в уравнении Коши имеет диагональный вид, то фазовый портрет имеет следующий вид

Если матрица имеет диагональный вид и корни равны, то имеем случай на рис. 35

6. ,

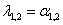
Рисунок 31 – Фазовый портрет

Рисунок 32 – Переходный процесс

Если матрица А имеет диагональный вид, то фазовый портрет изменится следующим образом.

Для уточнения фазовых траекторий используется метод изоклин.

Изоклина – это линия, соединяющая точки фазовых траекторий с одинаковым наклоном касательных. Для линейных систем изоклины представляют собой прямые и проходят через точку (0;0).

Изоклина определяется следующим образом:

Рисунок 34 – Уточнение фазового портрета методом изоклин

Фазовые портреты нелинейных систем.

Неопределенность:

В отличие от линейных систем, в нелинейных системах могут быть и особые линии.

Особые точки те же: центр, узел, фокус, седло и т.д.

Особые линии: устойчивый предельный цикл (фазовая траектория замкнута), неустойчивый предельный цикл, линия устойчивого положения, сепаратрисса (линия, разделяющая области с разным видом фазовых траекторий) и т.д.

Для выявления вида особых точек уравнение системы линеаризуется в их окрестности, определяются корни характеристического уравнения линеаризованной системы.

Уравнение изоклин:

Типовые случаи фазовых портретов нелинейных систем.

1. Устойчивый предельный цикл (автоколебания).

Фазовая траектория стремится к предельному циклу, следовательно, цикл устойчив.

Рисунок 35 – Фазовый портрет

Рисунок 36 – Переходный процесс

В данном случае система неустойчива в малом (точка (0;0) – неустойчивый фокус), но устойчива – в большом. Т.е. в малых значениях она будет расходиться, а при больших начальных условиях

2. Неустойчивый предельный цикл.

Рисунок 37 – Фазовый портрет

Рисунок 38 – Переходный процесс

Система в малом становится устойчивой (точка (0;0) – неустойчивый фокус), а в большом – неустойчивой.

Практически, неустойчивый предельный цикл ограничивает область начальных условий, в пределах которой система устойчива.

3. Несколько предельных циклов.

Рисунок 39 – Фазовый портрет

Рисунок 40 – Переходный процесс

Внешний предельный цикл устойчив, внутренний – неустойчив.

Рисунок 41 – Особая линия типа «сепаратриса»

Сепаратрисcа – особая линия, разделяющая области с различным видом фазовых траекторий.

Три особых точки: «центр» и две типа «седло». Всего на фазовой плоскости образовано 5 областей.

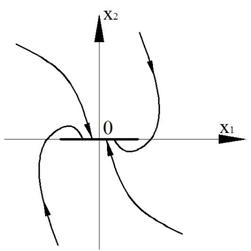
5. Отрезок установившихся состояний (отрезок покоя).

Фазовая траектория только входит в отрезок покоя. На отрезке скорость равна нулю (покой).

Рисунок 42 – Особая линия типа «отрезок покоя»

6. Скользящий процесс.

Рисунок 43 – Скользящий процесс

Если траектория приходит не на отрезок AB, то она преломляется на линии скользящего процесса и затем возвращается на отрезок.

При попадании на отрезок скользящего процесса, система начинает двигаться по линии скользящего процесса в направлении точки (0,0)

Практическое значение: в данном случае мы получаем желаемый переходный процесс с заданным законом движения. Это достижимо, если организовать соответствующее управление (нелинейный закон управления), что возможно далеко не всегда.

Рисунок 44 – Движение по линии скользящего процесса

В результате получаем процесс движения по отрезку скользящего процесса в виде колебаний относительно отрезка с амплитудой, стремящейся к нулю, и частотой, стремящейся к бесконечности.

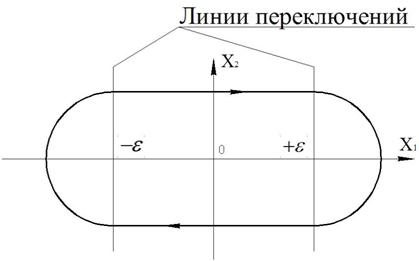
7. Линия переключений (нелинейный закон управления).

Рисунок 45 – Фазовый портрет системы

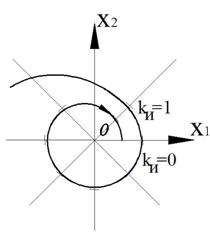
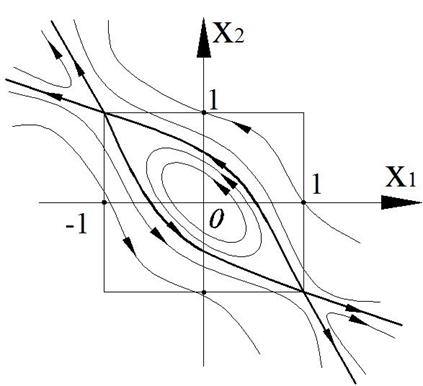
Пример. Построить фазовый портрет для системы, описываемой следующими уравнениями:

Условие 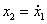не выполняется, следовательно направление фазовых траекторий может быть произвольным.

Разделим уравнение (2) на уравнение (1), получим дифференциальное уравнение фазовой траектории:

Особые точки и линии:

Решение дает 3 особые точки:

1) 2) 3)

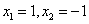
Для определения типа особых точек необходимо линеаризовать уравнение нелинейной системы в окрестности этих особых точек:

Далее символподразумевается, но не пишется.

1)

Для определения типа особой точки решаем характеристическое уравнение:

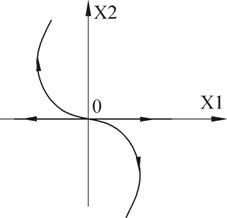
В итоге получаем чисто мнимые корни. Особая точка типа «центр» (фазовая траектория – эллипсы).

2)

Корни вещественные, разного знака. Особая точка типа «седло».

, k – коэффициент наклона асимптоты

Асимптоты действительны только в малой окрестности точки (1;-1)

3)

Далее аналогично пункту 2)

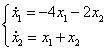
Определим направление фазовых траекторий: возьмем точку 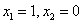и подставим в исходное нелинейное уравнение системы:

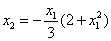
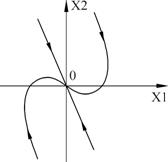
при с =1 (наклон касательной 45 о ): , изоклина пройдет через все особые точки.

Таким образом, получаем фазовый портрет

Рисунок 46 – Фазовый портрет

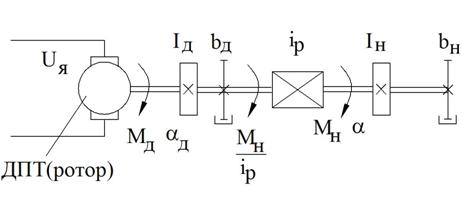
Изображение переходных процессов на фазовой плоскости на примере электромеханического следящего привода.

ДПТ – двигатель постоянного тока

ДС – датчик скорости

— механическая связь

— электрическая связь

— угол поворота выходного вала редуктора

Рисунок 47 – Структурная схема электромеханического следящего привода

Будем считать, что характеристики ДС и ДП линейные.

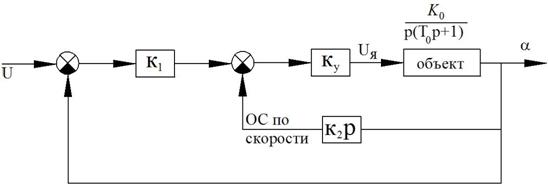
Пример 1. Следящий привод. Нагрузка: инерционная и вязкое трение.

Рисунок 48 – Структурная схема механической части объекта

— момент инерции двигателя

— момент инерции нагрузки

— передаточное отношение редуктора

— вязкое трение нагрузки

— коэффициент противоЭДС

— коэффициент усиления по моменту

— уравнение ДПТ

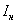
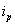
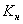
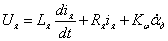
Введем допущение: в рабочем режиме ДПТ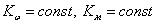(в реальной жизни – гистерезис)

Введем допущение: пренебрегаем электрической постоянной двигателя (на два порядка меньше, чем электромеханическая постоянная).

Уравнение моментов, приведенных к валу двигателя:

, где

Рисунок 49 – Объект управления

— описание объекта управления (интегрирующее звено с запаздыванием)

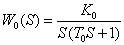
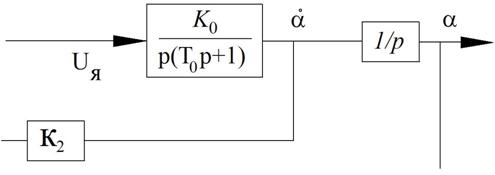
Необходимо найти уравнение регулятора:

Рисунок 50 – Пропорциональный интегральный регулятор

Обратная связь по скорости математически представлена верно, но на практике так делать нельзя из-за шумов (при дифференцировании не будет асимптоты).

При моделировании для исключения шумов необходимо изменить схему следующим образом:

Рисунок 51 – Изменения в схеме для моделирования

Уравнение регулятора с усилителем:

,

— колебательное звено.

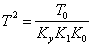
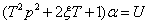
Обозначим:

Фазовые портреты при U=0

В соответствии уравнение линеаризованной системы принимает следующий вид:

2) Вычисления коэффициентов гармонической линеаризации для несимметричных колебаний

Причины несимметричных колебаний:

1) Несимметричные входные колебания;

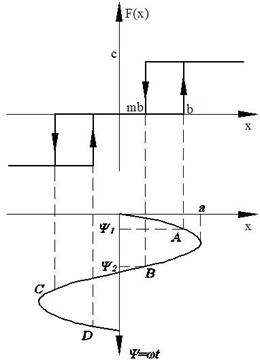
Решения будем искать в виде: x = x 0 + asin(ωt) = x 0 +x*, где x*= asin(ωt)

Уравнение системы можно разбить на 2 уравнения: для постоянной составляющей и для гармонического сигнала

3) Вычисление коэффициентов гармонической линеризации для симметричных колебаний

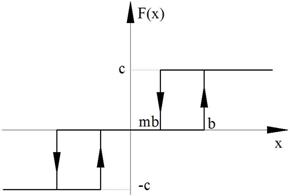
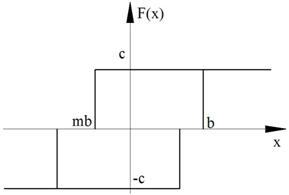
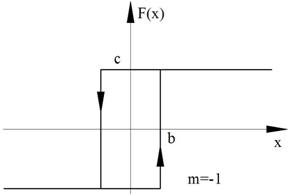
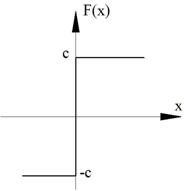
Упрощения: для однозначной нечётной симметричной функции F(x) коэффициент q`=0

Рисунок 96. Случай а)

Рисунок 97. Случай б)

Рисунок 98. Случай в)

Рисунок 99. Случай г)

Рисунок 100. Случай д)

Чтобы распечатать файл, скачайте его (в формате Word).

Источник