что такое броуновская частица 7 класс физика
Броуновская частица: понятие, размер, движение
Если размешать в воде тушь или краску, а потом посмотреть на эту воду под микроскопом, то можно увидеть быстрое перемещение мельчайших частичек сажи или краски в различных направлениях. Что провоцирует такие перемещения?
Кто и когда обнаружил
В 1827 году английский биолог Роберт Броун наблюдал в микроскоп за каплей воды, в которую случайно попало небольшое количество цветочной пыльцы. Он увидел, что мельчайшие частицы пыльцы приплясывают, двигаясь хаотично в жидкости. Так было открыто названное именем этого ученого броуновское движение – движение мельчайших частиц, растворенных в жидкости или газе. После наблюдения за различными видами пыльцы, имевшимися в его коллекции, биолог растворял в воде перетертые в порошок минералы.

В итоге Броун был убежден, что такое беспорядочное движение вызвано никак не самой жидкостью и не воздействием на жидкость извне, а непосредственно внутренним движением самой мелкой частицы. Эта частичка по аналогии с наблюдаемым движением получила название «броуновская частица».
Развитие теории, ее последователи
В дальнейшем открытие Броуна подтвердили, расширили и конкретизировали, основываясь на молекулярно-кинетической теории, А. Эйнштейн и М. Смолуховский. А французский физик Перрен спустя двадцать лет благодаря усовершенствованию микроскопов в процессе изучения беспорядочного движения броуновской частицы подтвердил существование собственно молекул. Наблюдение за броуновским движением позволило Перрену просчитать количество молекул в 1 моль любого газа и вывести барометрическую формулу.
Открытие движения броуновской частицы послужило доказательством существования гораздо более мелких, не видимых даже в микроскоп частичек – молекул жидкости и любого другого вещества. Именно молекулы своим постоянным движением заставляют перемещаться частички пыльцы, сажи или краски.
Определение и размер
Если смотреть в микроскоп на взвешенные в воде частицы туши, то можно заметить, что крупинки различного размера ведут себя по-разному. Относительно объемные частицы, испытывая за определенный отрезок времени одинаковое количество толчков со всех сторон, не начинают двигаться. А малые частицы за такой же временной интервал получают односторонние нескомпенсированные удары, толкающие их в сторону, и перемещаются.
Каков же размер броуновской частицы, подвергающейся воздействию молекул? Опытным путем доказано, что в движение приходят цитоплазматические зерна пыльцы размером не более 3 микрометров (мкм), или 10-6 метра, или 10-3 миллиметра. Частицы большего размера не становятся участниками обнаруженного Броуном постоянного движения.
Итак, ответим на вопрос «что такое броуновская частица». Это мельчайшие зерна вещества размером не более 3 мкм, находящиеся во взвешенном состоянии в жидкости или газе, совершающие постоянное хаотичное движение под воздействием молекул той среды, в которой они находятся.
Молекулярно-кинетическая теория
Броуновское движение не прекращается, не замедляется во времени. Это объясняет концепция молекулярно-кинетической теории, говорящей о том, что молекулы любого вещества находятся в постоянном тепловом движении. С повышением температуры среды скорость движения молекул увеличивается, соответственно ускоряется и броуновская частица, подвергающаяся ударам молекул.
Помимо температуры вещества, скорость броуновского движения зависит также от вязкости среды и размера взвешенной частицы. Максимальной скорости движение достигнет в том случае, когда будет высокая температура окружающего частицы вещества, само вещество не будет вязким, а пылинки будут наименьшего размера.
Молекулы вещества, в котором находятся мельчайшие частички, случайным образом сталкиваясь, прикладывают равнодействующую силу (производят толчок), вызывающую смену направления движения пыльцы. Но такие флуктуации очень непродолжительны во времени, и практически сразу направление прикладываемой силы меняется, что приводит к смене направления движения.
Самым простым и наглядным примером, позволяющим понять, что такое броуновская частица, является движение пылинок, видимое в косом солнечном луче. В 99-55 гг. до н. э. древнеримский поэт Лукреций совершенно точно объяснил причину беспорядочного движения в философской поэме «О природе вещей».
Вот посмотри: всякий раз, когда солнечный свет проникает
В наши жилища и мрак прорезает своими лучами,
Множество маленьких тел в пустоте, ты увидишь, мелькая,
Мечутся взад и вперед в лучистом сиянии света.
Можешь из этого ты уяснить себе, как неустанно
Первоначала вещей в пустоте необъятной мятутся.
Так о великих вещах помогают составить понятье
Малые вещи, пути намечая для их постиженья.
Кроме того, потому обратить тебе надо вниманье
На суматоху в телах, мелькающих в солнечном свете,
Что из нее познаешь ты материи также движения,
Происходящие в ней потаенно и скрыто от взора.
Ибо увидишь ты там, как много пылинок меняют
Путь свой от скрытых толчков и опять отлетают обратно,
Вечно туда и сюда разбегаясь во всех направленьях.
Задолго до появления современной увеличительной техники Лукреций, наблюдая аналог увиденного Броуном движения, пришел к выводу о существовании мельчайших частиц вещества. Броун подтвердил это, совершив одно из важнейших научных открытий.
Броуновское движение
Нам известно, что все вещества состоят из огромного числа очень и очень маленьких частиц, которые находятся в непрерывном и беспорядочном движении. Откуда нам это стало известно? Как учёные смогли узнать о существовании настолько маленьких частиц, которые ни в один оптический микроскоп невозможно увидеть? И уж тем более, как им удалось выяснить, что эти частицы находятся в непрерывном и беспорядочном движении? В этом учёным помогли разобраться два явления — броуновское движение и диффузия. Об этих явлениях мы и поговорим более подробно.
2. Броуновское движение
Английский учёный Роберт Броун не был физиком или химиком. Он был ботаником. И он совсем не ожидал, что откроет столь важное для физиков и химиков явление. И он не мог даже подозревать о том, что в своих довольно простых экспериментах он будет наблюдать результат хаотичного движения молекул. А это было именно так.
Что же это были за эксперименты? Они были почти такие же, что делают ученики на уроках биологии, когда с помощью микроскопа пытаются рассмотреть, например, клетки растений. Роберт Броун хотел рассмотреть в микроскоп пыльцу растений. Рассматривая зёрна пыльцы в капле воды, он заметил, что зёрна не находятся в покое, а непрерывно дёргаются, будто они живые. Наверное, сначала он так и подумал, но будучи учёным, конечно же отбросил эту мысль. Ему не удалось понять, почему эти зёрна пыльцы ведут себя таким странным образом, но он описал всё увиденное, и это описание попало в руки физиков, которые тут же поняли, что перед ними наглядное доказательство непрерывного и беспорядочного движения частиц.
Объясняется это движение, описанное Броуном, следующим образом: зёрна пыльцы достаточно велики, так что мы можем увидеть их в обычный микроскоп, а вот молекулы воды мы не видим, но, в то же время, зёрна пыльцы достаточно малы, чтобы из-за ударов по ним молекул воды, окружающих их со всех сторон, они смещались то в одну, то в другую сторону. То есть этот хаотичный «танец» зёрен пыльцы в капле воды показывал, что молекулы воды непрерывно и беспорядочно с разных сторон ударяют по зёрнам пыльцы и смещают их. С тех пор непрерывное и хаотичное движение мелких твёрдых частичек в жидкости или газе стали называть броуновским движением. Важнейшей особенностью этого движения является то, что оно непрерывное, то есть не прекращается никогда.
Диффузия — это ещё один пример наглядного доказательства непрерывного и беспорядочного движения молекул. И заключается оно в том, что газообразные вещества, жидкости и даже твёрдые вещества, хотя и намного медленнее, могут самоперемешиваться друг с другом. К примеру, запахи различных веществ распространяются в воздухе даже в отсутствие ветра именно благодаря этому самоперемешиванию. Или вот ещё пример — если в стакан с водой бросить несколько кристаллов марганцовки и, не перемешивая воду, подождать около суток, то мы увидим, что вся вода в стакане будет окрашена равномерно. Это происходит из-за непрерывного движения молекул, которые меняются местами, и вещества постепенно перемешиваются самостоятельно без внешнего воздействия.
4. Свойства броуновского движения и диффузии
Когда учёные-физики стали более подробно рассматривать явление, описанное Робертом Броуном, они заметили, что, как и диффузию, этот процесс можно ускорить, повышая температуру. То есть в горячей воде и окрашивание с помощью марганцовки будет происходить быстрее, и движение мелких твёрдых частичек, к примеру, графитовой крошки или тех же зёрен пыльцы, происходит с большей интенсивностью. Это подтверждало тот факт, что скорость хаотичного движения молекул напрямую зависит от температуры. Не вдаваясь в подробности, перечислим, от чего может зависеть и интенсивность броуновского движения, и скорость протекания диффузии:
2) от рода вещества, в котором эти процессы происходят;
3) от агрегатного состояния.
То есть при равной температуре диффузия газообразных веществ протекает значительно быстрее, чем жидкостей, не говоря уже о диффузии твёрдых тел, которая происходит настолько медленно, что её результат, и то очень незначительный, можно заметить или при очень высоких температурах, или за очень большое время — годы или даже десятилетия.
5. Практическое применение
Диффузия и без практического применения имеет огромное значение не только для человека, но и для всего живого на Земле: именно благодаря диффузии в нашу кровь через лёгкие попадает кислород, именно посредством диффузии растения добывают из почвы воду, поглощают углекислый газ из атмосферы и выделяют в ней кислород, а рыбы дышат в воде кислородом, который из атмосферы посредством диффузии попадает в воду.
Явление диффузии применяется и во многих областях техники, причём именно диффузии в твёрдых телах. К примеру, есть такой процесс — диффузионная сварка. В этом процессе детали очень сильно прижимаются друг к другу, нагреваются до 800 °C и посредством диффузии происходит их соединение друг с другом. Именно благодаря диффузии земная атмосфера, состоящая из большого количества различных газов, не разделяется на отдельные слои по составу, а везде примерно однородна — а ведь будь иначе, мы вряд ли смогли бы дышать.
Существует огромное количество примеров влияния диффузии на нашу жизнь и на всю природу, которые может найти любой из вас, если захочет. А вот о применении броуновского движения мало что можно сказать, кроме того, что сама теория, которая описывает это движение, может применяться и в других, казалось бы совершенно не связанных с физикой, явлениях. К примеру, эту теорию используют для описания случайных процессов, с применением большого количества данных и статистики — таких, как изменение цен. Теория броуновского движения используется для создания реалистичной компьютерной графики. Интересно, что человек, заблудившийся в лесу движется примерно так же, как и броуновские частички — блуждает из стороны в сторону, многократно пересекая свою траекторию.
6. Методические рекомендации учителям
1) Рассказывая классу о броуновском движении и диффузии, необходимо сделать акцент на том, что эти явления не доказывают факт существования молекул, но доказывают факт их движения и то, что оно беспорядочное — хаотичное.
2) Обязательно обратите особое внимание на то, что это непрерывное движение, зависящее от температуры, то есть тепловое движение, которое не может прекратиться никогда.
3) Продемонстрируйте диффузию с помощью воды и марганцовки, дав задание наиболее любознательным ребятам провести подобный эксперимент в домашних условиях и делая фотографии воды с марганцовкой через каждый час-два в течение дня (в выходной дети это с удовольствием сделают, а фото пришлют вам). Лучше, если в подобном эксперименте будет две ёмкости с водой — холодной и горячей, чтобы можно было продемонстрировать наглядно зависимость скорости диффузии от температуры.
4) Попробуйте измерить скорость диффузии в классе с помощью, к примеру, дезодоранта — в одном конце класса распыляем небольшое количество аэрозоля, а в 3-5 метрах от этого места ученик с секундомером фиксирует время, через которое он почувствует запах. Это и весело, и интересно, и запомнится детьми надолго!
5) Обсудите с детьми понятие хаотичности и тот факт, что даже в хаотических процессах учёные находят некие закономерности.
Броуновское движение
Броуновское движение — это беспорядочные перемещения малых частиц, возникающие вследствие их столкновения с невидимыми молекулами воды или газа. Первым его обнаружил ботаник Роберт Броун — частицы пыльцы, которые он разглядывал под микроскопом на мокром предметном стекле, двигались рывками, — однако описать математически смог только Альберт Эйнштейн. Броуновское движение объясняет, как распространяется в спокойном воздухе пыльца, но и описывает также множество случайных процессов — от наводнений до скачков на фондовом рынке. Его непредсказуемые рывки связаны с фракталами.
В XIX веке ботаник Роберт Броун, разглядывая под микроскопом частицы пыльцы, обнаружил, что они не стоят на месте, но отрывисто двигаются. На миг он задумался — уж не живые ли они? Нет, конечно, просто их сбивали с места молекулы воды, которой Броун смачивал предметные стекла. Частицы пыльцы двигались хаотично, иногда лишь немного, иногда на довольно большие расстояния, и, в конечном счете, совершали по стеклу путь, предсказать который было невозможно. И многие ученые начали задумываться над открытием Броуна, названным в его честь «броуновским движением».
Случайное блуждание
Броуновское движение совершается любыми малыми частицами, находящимися во взвешенном состоянии в жидкости или газе. Его можно наблюдать даже у довольно больших частиц, например частиц дыма, — при большом увеличении видно, какие зигзаги они описывают в воздухе. Сила получаемых частицами ударов зависит от импульса молекул. Она оказывается большей в случае тяжелых молекул жидкости либо газа — как и в случае быстро движущихся, например, молекул нагретой жидкости.
Во второй половине XIX века предпринималась не одна попытка описать броуновское движение математически, однако сделать это смог лишь Эйнштейн в 1905 году, когда он также опубликовал специальную теорию относительности и дал описание фотоэффекта, за что получил Нобелевскую премию. Эйнштейн воспользовался тепловой теорией, основанной на столкновениях молекул, и успешно объяснил движения частиц, которые наблюдал Броун. Поняв, что броуновское движение доказывает существование молекул жидкостей, физики вынуждены были принять и учение об атомах, которое даже в начале XX века еще вызывало сомнения.
Диффузия
Со временем броуновское движение способно заставить частицу пройти значительное расстояние, хоть, разумеется, и не такое, какое она могла бы пройти, если бы никто не мешал ей двигаться по прямой. Это объясняется случайным характером движения молекул, которые с равной вероятностью могут толкать ее и вперед, и назад. Поэтому, если уронить в жидкость плотную группу частиц, они начнут рассеиваться (диффундировать) во все стороны даже при том, что жидкость никто не будет помешивать и никакие потоки в ней не возникнут. Каждая частица пойдет по своему пути, и капля начнет расширяться, образуя диффузное облако. Такое рассеяние играет важную роль в распространении загрязнений воздуха, имеющих точечный источник, например в распространении аэрозоля в атмосфере. Даже при полном отсутствии ветра химические вещества будут рассеиваться в воздухе вследствие одного лишь броуновского движения.
Фракталы
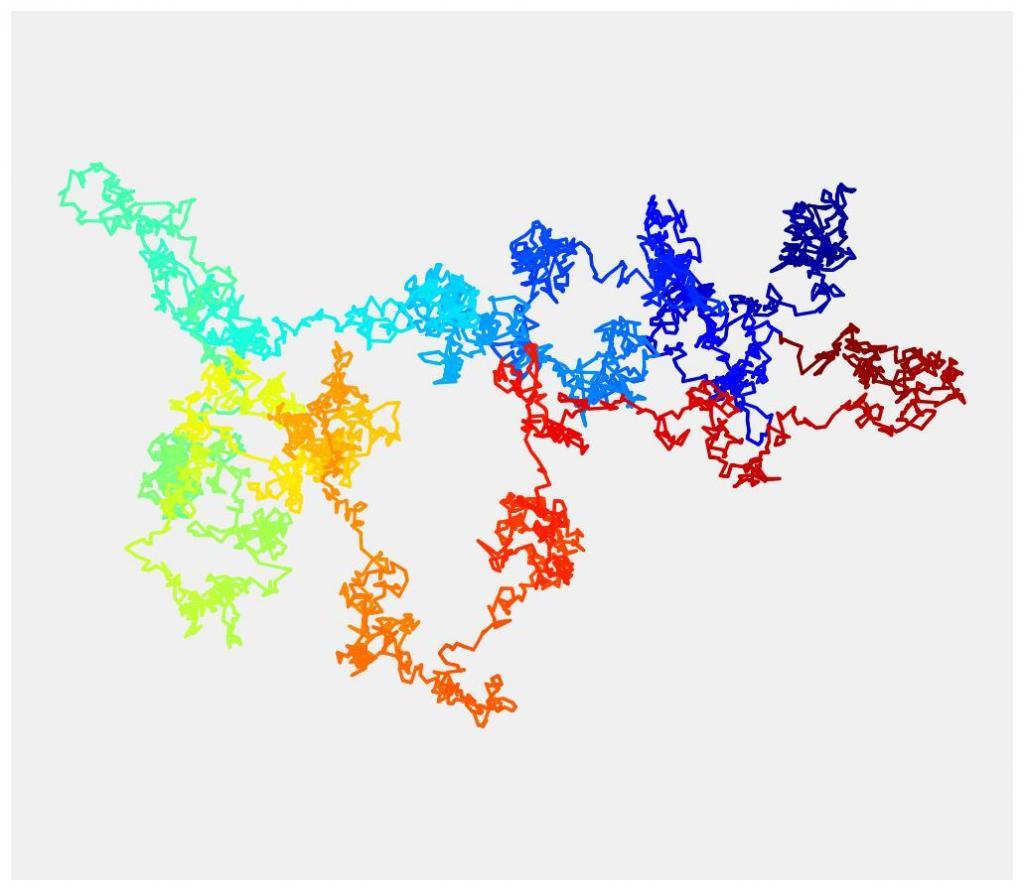
Путь, по которому следует частица, совершающая броуновское движение, дает нам пример фрактала. Каждый прямой отрезок этого пути может иметь любую длину и любое направление, однако некоторый общий рисунок все же существует. Этот рисунок несет в себе определенную структуру, в каком масштабе его ни разглядывай — от наименьшего из вообразимых до очень больших. А это и есть определяющее свойство фрактала.
Фракталы были в 1960-х и 1970-х предложены Бенуа Мандельбротом как метод представления самоподобных фигур в количественной форме. Фракталы — это фигуры, которые при любом масштабе выглядят одинаково. Если увеличить малый кусочек этой фигуры, вы увидите точно такую же, неотличимую от первой, рассматриваемой в большем масштабе, поэтому определить степень увеличения, глядя на фигуру, ни за что не удастся. Такая безмасштабная повторяемость часто встречается в природе — в рисунке береговой линии, в ветвях дерева, в листьях папоротника, в шестикратной симметрии снежинки.
Фракталы отличаются тем, что их длина или размерность не зависят от того, с каким увеличением вы их рассматриваете. Если вы решите измерить расстояние между двумя приморскими городами, Лендс-Эндом и Маунтс-Беем, то, скорее всего, придете к выводу, что оно составляет 30 км, однако вспомните про все береговые скалы и попробуйте обвить каждую веревкой — и вы обнаружите, что веревка вам понадобится в сотню километров длиной. Если же вы пойдете еще дальше и затеете обмерять каждую песчинку берега, веревку придется удлинить до многих сотен километров. Выходит, что абсолютная длина береговой линии зависит от масштаба, в котором вы проводите измерения. Ограничьтесь грубым очертанием берега — и вы снова вернетесь к уже знакомым вам 30 км. В этом смысле фрактальная размерность есть мера огрубления чего-то, будь то облако, дерево или горный хребет. Многие из фрактальных форм, например береговую линию, можно получить соединением шагов случайного движения — отсюда и их связь с броуновским движением.
Математика броуновского движения, или последовательность случайных шагов, может использоваться для создания фрактальных фигур, находящих применение во многих областях науки. С ее помощью можно создавать грубо очерченные виртуальные пейзажи — горы, деревья, облака — компьютерных игр, ее можно использовать в программах пространственного картирования, которые помогают роботам двигаться по сильно пересеченной местности, моделируя ее возвышенности и низины. Врачи применяют ее для медицинской визуализации, когда у них возникает нужда проанализировать структуру сложных органов тела, скажем легких, в которых ветвящиеся структуры присутствуют во всех масштабах, от грубого до совсем малого.
Идеи броуновского движения используются и для предсказания рисков либо событий будущего, которые являются суммарным результатом множества случайных воздействий — наводнений, колебаний фондового рынка. Фондовый рынок можно рассматривать как портфель ценных бумаг, стоимость которых варьируется случайным образом, напоминая броуновское движение множества молекул. Фигурирует оно и в моделировании других социальных процессов, относящихся к производству товаров и принятию решений. Броуновское движение с его случайным характером обладает значительным влиянием и появляется во множестве обличий — не в одном только танце чаинок в чашке горячего чая.
Что такое броуновская частица 7 класс физика
Вспомните из курса физики основной школы явление диффузии.
Чем может быть объяснено это явление?
Ранее вы узнали, что такое диффузия, т. е. проникновение молекул одного вещества в межмолекулярное пространство другого вещества. Это явление определяется беспорядочным движением молекул. Этим можно объяснить, например, тот факт, что объём смеси воды и спирта меньше объёма составляющих её компонентов.
Но самое очевидное доказательство движения молекул можно получить, наблюдая в микроскоп мельчайшие, взвешенные в воде частицы какого-либо твёрдого вещества. Эти частицы совершают беспорядочное движение, которое называют броуновским.
Броуновское движение — это тепловое движение взвешенных в жидкости (или газе) частиц.
Наблюдение броуновского движения.
Английский ботаник Р. Броун (1773—1858) впервые наблюдал это явление в 1827 г., рассматривая в микроскоп взвешенные в воде споры плауна.
Позже он рассматривал и другие мелкие частицы, в том числе частички камня из египетских пирамид. Сейчас для наблюдения броуновского движения используют частички краски гуммигут, которая нерастворима в воде. Эти частички совершают беспорядочное движение. Самым поразительным и непривычным для нас является то, что это движение никогда не прекращается. Мы ведь привыкли к тому, что любое движущееся тело рано или поздно останавливается. Броун вначале думал, что споры плауна проявляют признаки жизни.
Броуновское движение — тепловое движение, и оно не может прекратиться. С увеличением температуры интенсивность его растёт.
На рисунке 8.3 приведены траектории движения броуновских частиц. Положения частиц, отмеченные точками, определены через равные промежутки времени — 30 с. Эти точки соединены прямыми линиями. В действительности траектория частиц гораздо сложнее.
Объяснение броуновского движения.
Объяснить броуновское движение можно только на основе молекулярно-кинетической теории.
«Немногие явления способны так увлечь наблюдателя, как броуновское движение. Здесь наблюдателю позволяется заглянуть за кулисы того, что совершается в природе. Перед ним открывается новый мир — безостановочная сутолока огромного числа частиц. Быстро пролетают в поле зрения микроскопа мельчайшие частицы, почти мгновенно меняя направление движения. Медленнее продвигаются более крупные частицы, но и они постоянно меняют направление движения. Большие частицы практически толкутся на месте. Их выступы явно показывают вращение частиц вокруг своей оси, которая постоянно меняет направление в пространстве. Нигде нет и следа системы или порядка. Господство слепого случая — вот какое сильное, подавляющее впечатление производит эта картина на наблюдателя». R. Поль (1884—1976).
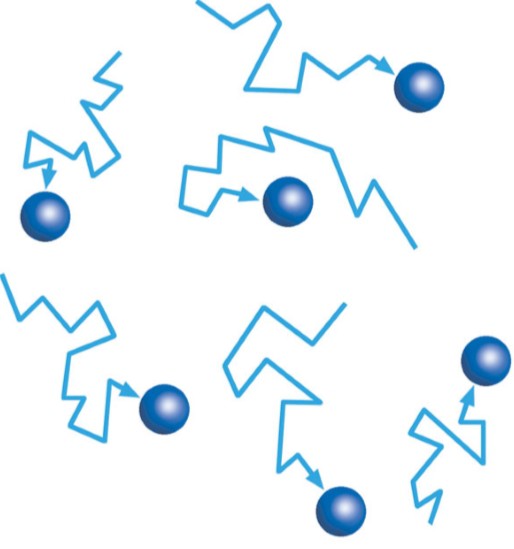
Причина броуновского движения частицы заключается в том, что удары молекул жидкости о частицу не компенсируют друг друга.
На рисунке 8.4 схематически показано положение одной броуновской частицы и ближайших к ней молекул.
При беспорядочном движении молекул передаваемые ими броуновской частице импульсы, например слева и справа, неодинаковы. Поэтому отлична от нуля результирующая сила давления молекул жидкости на броуновскую частицу. Эта сила и вызывает изменение движения частицы.
Молекулярно-кинетическая теория броуновского движения была создана в 1905 г. А. Эйнштейном (1879—1955). Построение теории броуновского движения и её экспериментальное подтверждение французским физиком Ж. Перреном окончательно завершили победу молекулярно-кинетической теории. В 1926 г. Ж. Перрен получил Нобелевскую премию за исследование структуры вещества.
Опыты Перрена.
Идея опытов Перрена состоит в следующем. Известно, что концентрация молекул газа в атмосфере уменьшается с высотой. Если бы не было теплового движения, то все молекулы упали бы на Землю и атмосфера исчезла бы. Однако если бы не было притяжения к Земле, то за счёт теплового движения молекулы покидали бы Землю, так как газ способен к неограниченному расширению. В результате действия этих противоположных факторов устанавливается определённое распределение молекул по высоте, т. е. концентрация молекул довольно быстро уменьшается с высотой. Причём чем больше масса молекул, тем быстрее с высотой убывает их концентрация.
Броуновские частицы участвуют в тепловом движении. Так как их взаимодействие пренебрежимо мало, то совокупность этих частиц в газе или жидкости можно рассматривать как идеальный газ из очень тяжёлых молекул. Следовательно, концентрация броуновских частиц в газе или жидкости в поле тяжести Земли должна убывать по тому же закону, что и концентрация молекул газа. Закон этот известен.
Перрен с помощью микроскопа большого увеличения и малой глубины поля зрения (малой глубины резкости) наблюдал броуновские частицы в очень тонких слоях жидкости. Подсчитывая концентрацию частиц на разных высотах, он нашёл, что эта концентрация убывает с высотой по тому же закону, что и концентрация молекул газа. Отличие в том, что за счёт большой массы броуновских частиц убывание происходит очень быстро.
Все эти факты свидетельствуют о правильности теории броуновского движения и о том, что броуновские частицы участвуют в тепловом движении молекул.
Подсчёт броуновских частиц на разных высотах позволил Перрену определить постоянную Авогадро совершенно новым методом. Значение этой постоянной совпало с ранее известным.